全數字接收機碼元同步的研究
馮明霞,張偉娟,徐坤玉
(蘭州交通大學 電子與信息工程學院 蘭州 730070)
0 引言
在全數字接收機中,同步技術是一項非常關鍵的技術,同步系統工作性能的好壞,很大程度上決定了通信系統的質量。接收端沒有恢復同步,則不能確定發射端的信息,會造成通信無法完成的狀況。碼元同步是接收端產生的一個與接收信號符號速率相同,相位與最佳判決時刻一致的定時脈沖序列信號。在全數字接收機中。由于解調前對信號采用異步采樣。為了解決位同步問題,提出了Gardner算法。Gardner算法在一個碼元中需要2個樣點就能進行判決,所以在碼元同步算法中有廣泛的應用。
1 Gardner符號定時同步環路
圖1為Gardner符號定時同步環路,A/D轉換器以獨立時鐘對接收到的模擬信號進行采樣。
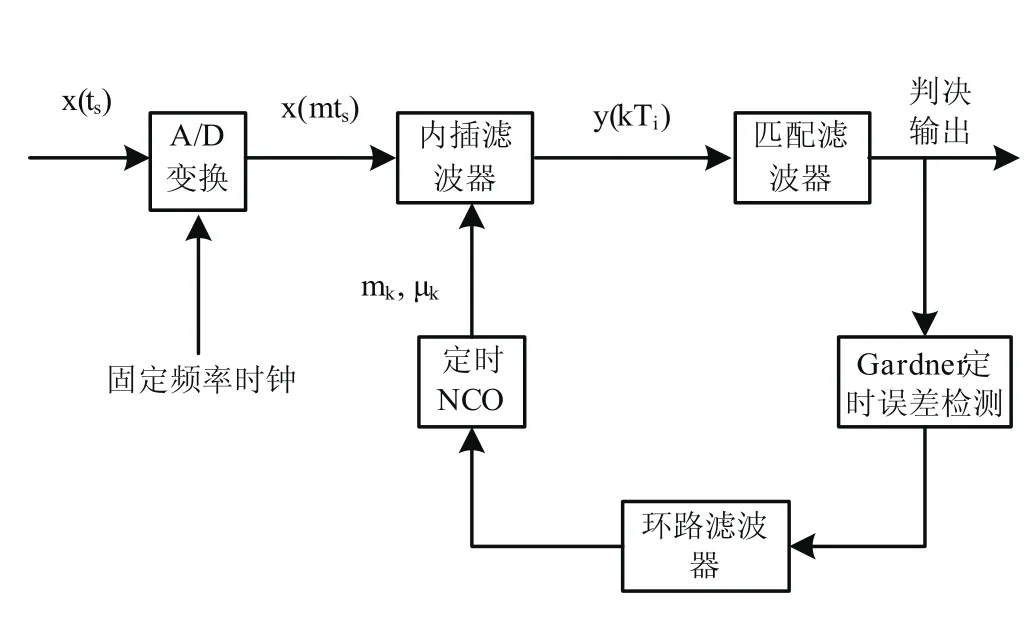
圖1 Gardner符號定時同步環路
Gardner符號定時同步環路[5]主要由Gardner定時誤差檢測,環路濾波器,數控振蕩器及內插濾波器組成。數控振蕩器根據Gardner定時誤差檢測出的時鐘相位誤差,獲得內插濾波器的控制量mk,μk。經過時鐘同步后產生插值信號y(kTi),設調制信號的符號周期為T,則Ti=T/k (k為一小整數),最后判決輸出。
1.1 內插濾波器
插值理論是根據一條曲線上已知的幾個樣本點(插值節點),得到一個插值函數,通過這個插值函數得到這條曲線上其他未知的點。內插濾波器在同步電路中是非常重要的部分,用插值的方法對本地定時相位進行調整,使得采樣的結果盡可能接近最佳采樣點。設hI(t)為內插濾波器的沖擊響應,濾波器的輸出信號[4]具體可以為:

其中mk為內插基點,μk為定時誤差。
從時域角度對內插濾波器分析,限帶信號x(t)經過獨立時鐘Ts采樣后成為時域離散信號x(mTs),輸入到內插濾波器。內插濾波器與控制單元輸出的符號使能配合,恢復出符號值y(kTi),Ti即符號周期。將插值時刻與采樣時刻用整數標記,來表示它們的關系如圖2所示。

圖2 插值過程
根據基于Farrow結構的三階拉格朗日插值法[3]計算內插濾波器的系數[6]。
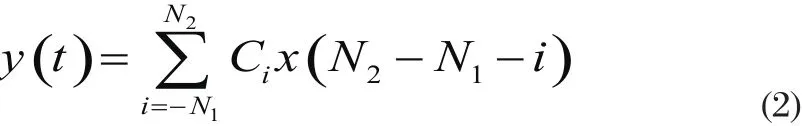
其中Ci為濾波器的系數。
1.2 Gardner定時誤差檢測
本文采用的是Gardner提出的定時誤差算法。Gardner算法[2]是一種在載波同步之前先進行定時同步,該算法的數學表達式如下:
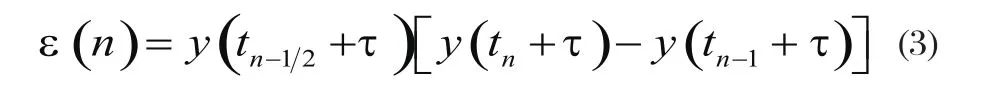
其中,ε(n)代表第n個符號的定時誤差;y(tn+τ)和y(tn-1+τ)分別表示當前符號與前一符號的最佳判決點,它們的差的極性反映了定時誤差調整的方向;y(tn-1/2+τ)表示2個相鄰符號的最佳判決點中間的采樣點,其數值表征了定時誤差的大小。
算法具有兩個特點:一是每個符號只需要兩個采樣點,且以碼元速率輸出誤差信號;二是估計算法是獨立于載波相位的,即可以在載波相位同步之前,進行定時誤差估計[1]。
1.3 環路濾波器
環路濾波器采用理想積分濾波器,其傳遞函數在s域上表示為:
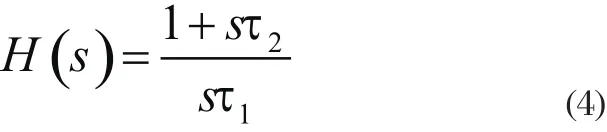
變換到z域為:
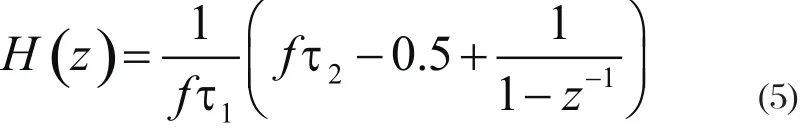
進而得到離散域的環路濾波器的遞歸方程為:
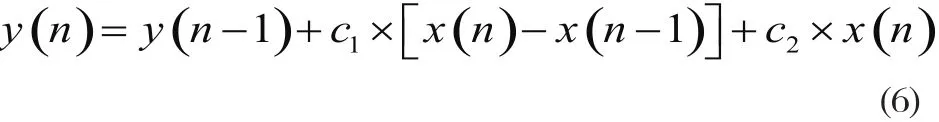
1.4 定時NCO
NCO由采樣時鐘fs驅動,T為符號間隔,Ti為NCO輸出周期。NCO每溢出一次,表示當前插值濾波器要計算一次內插值,這就相當于確定插值基點mk[7]的過程。設第k個時鐘時期NCO寄存器的值為η(m),NCO的步進控制字為W(m),則NCO寄存器的內容為:

步進控制字W(m)受到符號同步環路的控制,在環路鎖定情況下,W(m)接近于常數。因此在每個時鐘周期,NCO寄存器值減少1/W(m),NCO的輸出周期Ti=Ts/ W(m),即:
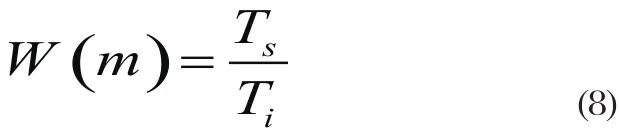
從式(8)可以看出,W(m)為插值器周期Ti的同步估計。下面說明μk[8]的計算過程,在連續時間情況下,NCO寄存器值的變化曲線如圖3所示。
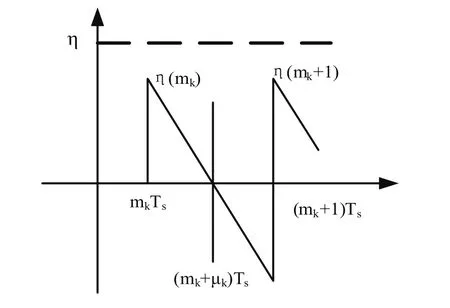
圖3 NCO寄存器值的變化
在圖3中橫軸為時間,縱軸為寄存器值。根據相似三角形的知識,很容易得到:
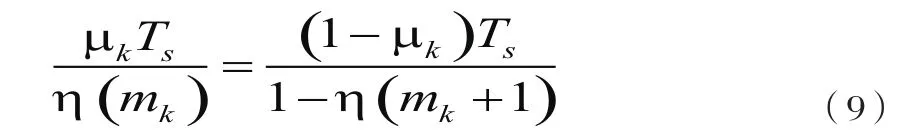
解得
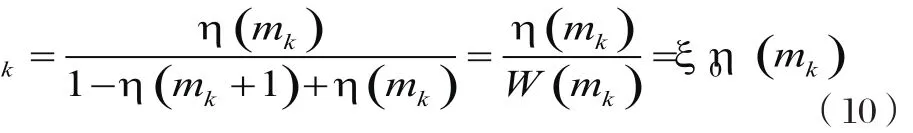
2 系統性能仿真分析
環路對定時相位偏差和頻率偏差的校正能力體現了定時環路的性能。前面對定時環路進行了分析,構建環路的仿真模型[7]如下:
收發端采用均方根升余弦濾波器,滾降系數為0.25。在信道中加入噪聲,信噪比是30,加入定時相位偏差π/2和頻率偏差,頻率偏差百分比是0.1。用于位同步測試的調制數據,經過解調端的數字下變頻,以及匹配濾波器處理,得到的測試數據的星座圖如圖4所示,星座圖是錯亂的。經過位定時環路,抽取后的IQ兩路數據星座圖如圖5所示,星座圖反映了解調出數據的4種相位。在較理想的環境下很快μk就穩定下來了,說明此算法性能良好。穩定下來后的輸出如圖6所示。

圖4 調制信號的星座圖

圖5 位定時星座圖

圖6 定時誤差輸出
3 結論
本文在全面分析碼元同步原理的基礎上,提出了一種內插和Gardner定時誤差檢測相結合實現碼元同步電路的設計方案,并詳細介紹了各模塊的設計和實現方法,通過仿真實驗進行了驗證。Gardner算法由于一個碼元只需要取2個樣點就可以進行定時誤差估計,所以降低了采樣頻率的要求,同時計算也較簡單,在軟件無線電中得到了較廣泛的應用。
[1]F.M. Gardner. A BPSK/QPSK Timing-error Detector for Sampled Receivers[J]. IEEE Trans. Commun.,1986,com-34(5): 423-429.
[2]F.M. Gardner. Interpolation in Digital Modems-Part I:Fundamentals[J]. IEEE Trans. Commun., 1993, com-41(3): 501-507.
[3]L.Erup, F.M.Gardner and R.A.Harris. Interpolation in Digital Modems-Part II: Implementation and Performance[J]. IEEE Trans. Commun., 1993, corn-41(3): 998-1008.
[4]張公禮.全數字接收機理論與技術[M]. 北京:科學出版社, 2005.
[5]李濤,李驛華,陳星.接收機碼元同步算法的研究[J].電子測量技術, 2006(5): 165-166.
[6]朱雪陽.基于Gardner算法的位定時同步研究[D].南京:南京理工大學, 2010.
[7]隋德良.QPSK中頻全數字解調器的設計與FPGA實現[D].南京:南京理工大學, 2010.
[8]李媛媛,徐巖,王靖岳.對MATLAB實現數字信號的QPSK的頻譜分析[J].通信技術,2008,41(01):41-43.

