基于T-GOWA和T-IGOWA算子的二元語義多屬性決策方法
劉 兮,陳華友,周禮剛
(安徽大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,合肥 230039)
0 引言
自Yager[1]于1988年提出了有序加權(quán)平均(OWA)算子后,OWA算子作為一種數(shù)據(jù)信息集成算子在決策、管理、人工智能、專家系統(tǒng)等諸多領(lǐng)域迅速得到了很廣泛的應(yīng)用。1999年Yager又提出一種誘導(dǎo)有序加權(quán)平均(IOWA)算子[2],該算子先是通過誘導(dǎo)變量對(duì)數(shù)據(jù)進(jìn)行排序,然后加權(quán)集成,它是OWA算子的一種推廣形式。最近文獻(xiàn)[3]提出了一種廣義OWA(GOWA)算子,GOWA算子是在OWA算子上增加一個(gè)新參數(shù)來控制變量值的變化程度,是OWA算子的拓展。文獻(xiàn)[4]把GOWA算子拓展到直覺模糊環(huán)境,提出了直覺模糊多屬性決策問題的GOWA方法。文獻(xiàn)[5]將GOWA算子和IOWA算子相結(jié)合,提出了誘導(dǎo)廣義有序加權(quán)平均(IGOWA)算子。
在許多現(xiàn)實(shí)決策中,由于問題自身的復(fù)雜性和信息的模糊、不確定性,決策者往往難以用定量化的方法來描述決策信息,而一般較好的選擇是采用定性的語言形式來表示。需要指出的是,在對(duì)決策者的語言評(píng)價(jià)信息進(jìn)行集結(jié)時(shí),得到的結(jié)果往往不能夠用預(yù)先定義的語言評(píng)價(jià)集中的元素來準(zhǔn)確表達(dá),只能近似的表示出來,這就造成了信息的損失和集結(jié)結(jié)果的不精確性。為此,西班牙學(xué)者Herrera等人于2000年首次提出了關(guān)于語言信息集結(jié)的二元語義分析方法[6],較好地克服了這類缺陷,同時(shí)還提出了基于二元語義有序加權(quán)平均(T-OWA)算子,并將其成功應(yīng)用于多粒度語言信息的多屬性決策之中[7]。文獻(xiàn)[8]提出了二元語義有序加權(quán)幾何(T-OWG)算子,分析了T-OWA算子和T-OWG算子的性質(zhì)。文獻(xiàn)[9]提出了二元語義混合加權(quán)平均(T-HWA)算子,并指出二元語義加權(quán)算術(shù)平均(T-WA)算子和T-OWA算子均為T-HWA算子的特例。文獻(xiàn)[10]將IOWG算子推廣到二元語義中,提出了二元語義誘導(dǎo)有序加權(quán)幾何(T-IOWG)算子,并分析了其性質(zhì),最后提出一種基于T-IOWG算子的二元語義多屬性群決策方法。本文把GOWA算子和IGOWA算子拓展到二元語義環(huán)境中,提出了二元語義廣義有序加權(quán)平均(T-GOWA)算子和二元語義誘導(dǎo)廣義有序加權(quán)平均(T-IGOWA)算子,并探討了這些算子的一些性質(zhì)和特例,最后基于這些算子,分別在單人決策和群決策這兩種情形下,提出了屬性權(quán)重已知且屬性值為語言信息形式給出的多屬性決策方法。實(shí)例分析的結(jié)果表明該方法是有效的和可行的。
1 主要概念和結(jié)論
1.1 二元語義
二元語義是采用一個(gè)二元組(sk,ak)來表示語言評(píng)價(jià)信息的方法,其中元素sk是預(yù)先定義好的語言評(píng)價(jià)集ST中的第k個(gè)元素;ak為符號(hào)轉(zhuǎn)移值,且滿足ak∈[ )-0.5,0.5,表示經(jīng)過集結(jié)計(jì)算后得到的語言信息與最貼近元素sk之間的差別。這里ST是由奇數(shù)個(gè)元素構(gòu)成的有序語言評(píng)價(jià)集,即T稱為ST的粒度。一般要求ST滿足:(1)有序性:當(dāng)i≥j時(shí),有(2)存在逆運(yùn)算算子:,其中j=T-i;(3)極大化運(yùn)算和極小化運(yùn)算:當(dāng)時(shí),有
定義1[6,7]若sk∈ST為語言短語,令函數(shù):θ(sk)=(sk,0),sk∈ST,則稱θ:ST→ST×[ )-0.5,0.5為語言短語對(duì)應(yīng)的二元語義形式的轉(zhuǎn)換函數(shù)。
定義2[6,7]設(shè)β∈[0,T-1]為語言評(píng)價(jià)集ST經(jīng)某集結(jié)方法得到的實(shí)數(shù),令:

則稱函數(shù) Δ:[0,T-1]→ST×[ )-0.5,0.5為實(shí)數(shù)β對(duì)應(yīng)的二元語義信息的轉(zhuǎn)換函數(shù),其中round為四舍五入取整算子。
定義3[6,7]設(shè)(sk,ak)是一個(gè)二元語義信息,sk為ST中第k個(gè)元素,ak∈[- 0.5,0.5 ),令 Δ-1(sk,ak)=k+ak=β,則稱Δ-1:ST×[- 0.5,0.5)→[0,T-1]為轉(zhuǎn)換函數(shù)Δ的逆函數(shù)。Δ-1的意義在于把二元語義信息轉(zhuǎn)換為相應(yīng)的實(shí)數(shù)。
假設(shè)(sk,ak)和(sl,al)為兩個(gè)二元語義,其序關(guān)系滿足[6,7]:(1)若k>l,則 (sk,ak)> (sl,al),(2)當(dāng)k=l時(shí),若ak>al,則(sk,ak)>(sl,al);若ak=al,則(sk,ak)=(sl,al)。
1.2 T-GOWA算子和T-IGOWA算子
定義4[6]設(shè){(s1,a1),(s2,a2),…,(sn,an)}是一組二元語義信息,w=(w1,w2,…,wn)T為相應(yīng)的權(quán)重向量,且:

則稱Φ為二元語義加權(quán)算術(shù)平均(T-WA)算子。特別地,當(dāng)wj=1/n,j=1,2,…,n時(shí),則算子Φ退化為二元語義算術(shù)平均算子。
定義5[6]設(shè){(s1,a1),(s2,a2),…,(sn,an)}是一組二元語義信息,令:

其中(δ(1),δ(2),…,δ(n))是 (1,2,…,n)的一個(gè)置換,使得(sδ(j-1),aδ(j-1))≥(sδ(j),aδ(j)),j=2,3,…,n,且:
ω=(ω1,ω2,…,ωn)T是與函數(shù) Ω 相關(guān)聯(lián)的權(quán)重向量,,則稱Ω為二元語義有序加權(quán)平均(T-OWA)算子。
定義6[3]設(shè)fω:Rn→R,若:

其中ω=(ω1,ω2,…,ωn)T是與fω相關(guān)的加權(quán)向量,滿足且bj是實(shí)數(shù)a1,a2,…,an中按從大到小的順序排列的第j個(gè)大的數(shù),參數(shù)λ∈(0,+∞),則稱函數(shù)fω是n維廣義有序加權(quán)平均算子,簡(jiǎn)記為GOWA算子。
定義7[5]設(shè)為n個(gè)二維數(shù)組,gω:Rn→R,若:

則稱函數(shù)gω是由u1,u2,…,un所產(chǎn)生的n維誘導(dǎo)廣義有序加權(quán)平均算子,簡(jiǎn)記為IGOWA算子,uj稱為aj的誘導(dǎo)值。其中u-index(j)是u1,u2,…,un中按從大到小的順序排列的第j個(gè)大的數(shù)所對(duì)應(yīng)的下標(biāo),ω=(ω1,ω2,…,ωn)T是與IGOWA算子相關(guān)的加權(quán)向量,滿足j=1,2,…,n,參數(shù)λ∈(0,+∞)。

定義8設(shè){(s1,a1),(s2,a2),…,(sn,an)}是一組二元語義信息,若其中ω=(ω1,ω2,…,ωn)T是與函數(shù)?相關(guān)聯(lián)的權(quán)重向量,,參數(shù)λ∈(0,+∞),且是按照序關(guān)系確定的(s1,a1),(s2,a2),…,(sn,an)中第j大的元素,則稱?為二元語義廣義有序加權(quán)平均(T-GOWA)算子。
由定義8可得到以下幾個(gè)結(jié)論:
(1)當(dāng)λ=1 時(shí),有則T-GOWA算子轉(zhuǎn)化為 T-OWA算子;
(2)當(dāng)λ→0+時(shí),有,則T-GOWA算子轉(zhuǎn)化為 T-OWG算子。

顯然,由定義9也可得到以下幾個(gè)結(jié)論:
(1)當(dāng)λ=1時(shí),有,則T-IGOWA算子轉(zhuǎn)化為T-IOWA算子;
(2)當(dāng)λ→0+時(shí),有則 T-IGOWA 算子轉(zhuǎn)化為T-IOWG算子。
1.3 T-GOWA算子和T-IGOWA算子的性質(zhì)
關(guān)于T-GOWA算子,具有如下的性質(zhì):
性質(zhì)1(置換不變性)設(shè)(s′1,a′1),(s′2,a′2),…,(s′n,a′n)是(s1,a1),(s2,a2),…,(sn,an)的任一置換,那么集結(jié)二元語義信息所得結(jié)果與集結(jié)的先后次序無關(guān),即:

性質(zhì)2(冪等性)設(shè)(s1,a1),(s2,a2),…,(sn,an)是一組二元語義信息,若對(duì)?j,有(sj,aj)=(s,a),則:
?[(s1,a1),(s2,a2),…,(sn,an)]=(s,a)證明:因?yàn)閷?duì) ?j,有 (sj,aj)=(s,a),則,則:

性質(zhì)3(單調(diào)性)設(shè)(s1,a1),(s2,a2),…,(sn,an)和(s′1,a′1),(s′2,a′2),…,(s′n,a′n)是兩組二元語義信息,在權(quán)重向量ω不變的情形下,若對(duì) ?j,有 (sj,aj)≥(s′j,a′j),則:

證明:由于:

兩邊取自然對(duì)數(shù)可得:

再兩邊對(duì)Δ-1(s·j,a·j)求導(dǎo)可得:

又因?yàn)閷?duì) ?j,有 (sj,aj)≥(s′j,a′j),可得則
故:

性質(zhì)4設(shè)?為T-GOWA算子,且?=?(λ),λ1≥λ2,則:?(λ1)≥?(λ2)
性質(zhì)5(有界性)T-GOWA算子介于max算子和min算子之間,即:

故結(jié)論成立。
可以證明T-IGOWA算子也存在與T-GOWA算子類似的性質(zhì),只是運(yùn)算法則不同,限于篇幅,這里不再贅述。
2 2T-GOWA算子和T-IGOWA算子的應(yīng)用
下面基于T-GOWA算子和T-IGOWA算子,對(duì)屬性權(quán)重已知且屬性值以二元語義信息形式給出的多屬性決策方法進(jìn)行探討:
2.1 T-GOWA算子在單人決策的應(yīng)用
在單人決策的情況下,我們給出一種基于T-GOWA算子的多屬性決策方法,具體步驟如下:
步驟1:對(duì)于某一多屬性決策問題,設(shè)A={A1,A2,…,Am}為方案集,G={G1,G2,…,Gn}為屬性集,屬性權(quán)重向量為決策者對(duì)方案Ai按照預(yù)先定義好的語言評(píng)價(jià)集…,T-1}}關(guān)于屬性Gj進(jìn)行測(cè)度,得到屬性值rij(rij∈ST),從而構(gòu)成決策矩陣R=(rij)m×n
步驟2:利用權(quán)重向量w和決策矩陣R=(rij)m×n得到加權(quán)二元語義決策矩陣,其中

步驟3:利用T-GOWA算子對(duì)R按行進(jìn)行集結(jié),得到各方案的綜合屬性值

步驟4:根據(jù)二元語義的序關(guān)系對(duì)各方案綜合屬性值Li(ω)進(jìn)行方案的排序和選優(yōu)。
2.2 T-IGOWA算子在群決策的應(yīng)用
在大型決策或者重要決策的過程中,為體現(xiàn)決策的民主性和合理性,往往需要多個(gè)決策者共同參與,下面給出一種基于T-IGOWA算子的多屬性群決策方法,具體步驟如下:
步驟1:設(shè)A、G分別為方案集和屬性集,屬性權(quán)重向量為,d2,…,dt}為決策者集,τ={τ1,τ2,…,τt}是t位決策者的權(quán)重向量,設(shè)決策者dk∈D給出方案Ai∈A在屬性Gj∈G下的屬性值,從而構(gòu)成決策矩陣
步驟2:利用T-WA算子和權(quán)重向量w=[w1,w2,…,wnT]對(duì)R(k)中第i行進(jìn)行集結(jié),得到?jīng)Q策者dk對(duì)方案Ai的綜合屬性值

步驟3:利用T-IGOWA算子對(duì)t位決策者給出的方案Ai的綜合屬性值進(jìn)行集結(jié),得到方案Ai的群體綜合屬性值

其中 (rτ-index(l),aτ-index(l))是τ1,τ2,…,τt中第l大的元素所對(duì)應(yīng)的二維數(shù)組中的第二個(gè)分量ω=(ω1,ω2,…,ωt)T是與T-IGOWA算子相關(guān)聯(lián)的權(quán)重向量參數(shù)λ∈(0,+∞)由決策者根據(jù)實(shí)際情況預(yù)先選擇確定。
步驟4:根據(jù)二元語義的序關(guān)系對(duì)各方案綜合屬性值Li(τ,ω)進(jìn)行方案的排序和選優(yōu)。
3 實(shí)例分析
某個(gè)風(fēng)險(xiǎn)投資公司進(jìn)行項(xiàng)目投資評(píng)估,有4個(gè)備選企業(yè)Ai(i=1,2,3,4),4個(gè)評(píng)價(jià)屬性Gj(j=1,2,3,4)(屬性分別為風(fēng)險(xiǎn)因素、成長(zhǎng)因素、社會(huì)政治影響因素和環(huán)境影響因素),屬性權(quán)重為w=(0 .25,0.3,0.2,0.25)T。該公司聘請(qǐng)三位專家dk(k=1,2,3)參與決策分析,專家權(quán)重為τ=(0.3,0.5,0.2),利用語言評(píng)價(jià)集所得語言評(píng)估矩陣為:

下面利用2.2提出的方法進(jìn)行方案排序:
步驟1:利用T-WA算子和權(quán)重向量w=(0.25,0.3,0.2,0.25)T對(duì)R(k)中第i行進(jìn)行集結(jié),得到?jīng)Q策者dk對(duì)方案Ai的綜合屬性值
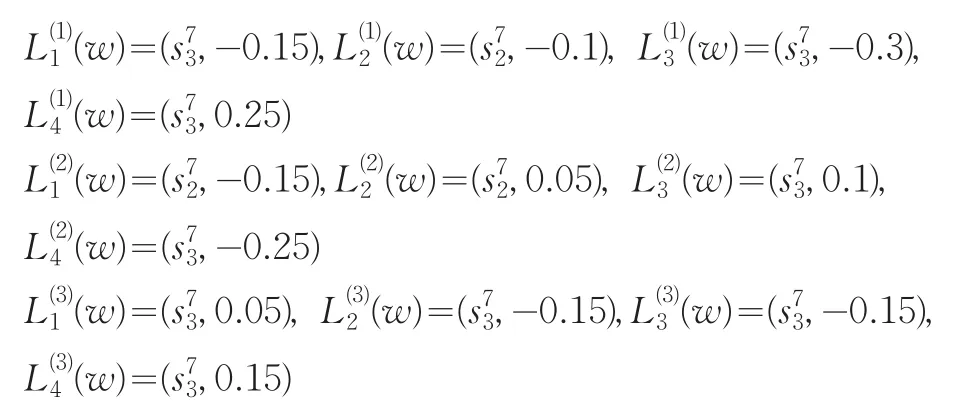
步驟2:再利用T-IGOWA算子對(duì)t位決策者給出的方案Ai的綜合屬性值進(jìn)行集結(jié),這里與T-IGOWA算子相關(guān)聯(lián)的權(quán)重向量為ω=(0 .3,0.4,0.3)T,專家權(quán)重為τ=(0.3,0.5,0.2),得到各方案Ai的群體綜合屬性值:

當(dāng)參數(shù)λ取一些特殊值時(shí),Ai的群體綜合屬性值如表1。步驟3:根據(jù)二元語義的序關(guān)系,得到方案排序如表2。可見最優(yōu)方案為A4。

表1

表2
4 結(jié)束語
本文針對(duì)二元語義信息的集結(jié)問題,將傳統(tǒng)的GOWA算子和IGOWA算子進(jìn)行拓展,提出了一些新的集結(jié)算子:二元語義廣義有序加權(quán)平均(T-GOWA)算子和二元語義誘導(dǎo)廣義有序加權(quán)平均(T-IGOWA)算子,探討了這些算子的性質(zhì)和特例,并把它們應(yīng)用于屬性權(quán)重已知且屬性值為語言信息形式給出的多屬性決策中。該決策方法不僅充分考慮了各決策者的重要性,而且參數(shù)的不同使決策者能夠有更寬泛的選擇,具有很好的實(shí)用價(jià)值。
[1] Yager R R.On Ordered Weighted Averaging Aggregation Operators in Multi-criteria Decision Making[J].IEEE Transactions on Systems,Man,and Cybernetics,1988,(18).
[2] Yager R R,Filev D P.Induced Ordered Weighted Averaging Operators[J].IEEE Transactions on Systems,Man,and Cybernetics,1999,(29).
[3] Yager R R.Generalized OWA Aggregation Operators[J].Fuzzy Optimization and Decision Making,2004,(3).
[4] 伍之前,李登峰.基于GOWA算子的直覺模糊多屬性決策方法[J].運(yùn)籌與管理,2010,19(3).
[5] J M Merigo,A M Gil-Lafuente.The Induced Generalized OWA Operator[J].Information Sciences,2009,(179).
[6] Herrera F,Martinez L.A 2-tuple Fuzzy Linguistic Represen-tation Model for Computing with Words[J].IEEE Transactions on Fuzzy Systems,2000,8(12).
[7] Herrera F,Martinez L.A Model Based on Linguistic 2-tuples for Dealing with Multi-granular Hierarchical Linguistic Contexts in Multi-expert Decision-making[J].IEEE Transactions on Systems,Man and Cybernetics,2001,31(2).
[8] 姜艷萍,樊治平.二元語義信息集結(jié)算子的性質(zhì)分析[J].控制與決策,2003,18(6).
[9] 魏峰,劉淳安,劉三陽.基于不確定信息處理的語言群決策方法[J].運(yùn)籌與管理,2006,15(3).
[10] 衛(wèi)貴武.基于T-OWG和T-IOWG算子的二元語義多屬性群決策方法[J].統(tǒng)計(jì)與決策,2008,(10).

