T檢驗失效的原因及處理

穆廣杰

(鄭州航空工業管理學院,鄭州 450015)

T檢驗，亦稱student t檢驗（Student's t test），主要用于樣本容量較小（例如n＜30），總體方差δ2未知的正態分布數據。用來判斷樣本與樣本，樣本與總體的差異是由抽樣誤差引起還是本質差別造成的統計推斷方法。亦稱“顯著性檢驗（Test of statistical significance）”，其基本原理是先對總體的特征做出某種假設，然后通過抽樣樣本的統計推斷，做出對此假設應該被拒絕還是接受的推斷。其基本思想是小概率反證法。小概率是指小概率事件（P＜0.01或P＜0.05）在一次試驗中基本上不會發生。反證法是先提出檢驗假設H0，再用適當的統計方法確定假設成立的可能性大小，如可能性小,則認為假設不成立，若可能性大，則還不能認為假設不成立，在實際工作中T檢驗使用范圍較廣。但也存在著局限性，即T檢驗的失效。充分研究其產生失效性的理論基礎避免使用時錯誤，并對T檢驗的失效可能造成的后果有所控制，可以使其發揮更大的作用

1 參數T檢驗的失效

假設檢驗根據問題的要求，設是A關于總體分布的一項命題，所有使命題A成立的總體分布構成一個集合HA，稱為原假設H0，使命題A不成立的所有總體分布構成另一個集合HB，稱為備擇假設H1。對一個假設H0進行檢驗，就是制定一個規則，使得有了樣本以后，根據這規則可以決定是接受（即承認命題A正確）,還是拒絕它（即否認命題A正確）。這樣，所有可能的樣本所組成的樣本空間被劃分為兩部分HA和HB(HA的補集)，HA?HB=φ，當樣本x∈HA時,接受假設H0，拒絕H1；當x∈HB時,拒絕H0，接受H1。用檢驗進行分析判斷，以接受一個，拒絕另一個。命題的對立性及“僅選其一”的規定，從邏輯上來說，應當不會出現兩者都接受或都拒絕這樣的兩可結論。但是實際中存在這樣的情況：兩個對立命題HA和HB，以同一樣本數據進行檢驗，當以HA為H0時，接受H0，即接受HA；當以HB為H0時，結果同樣是接受H0，即接受HB。出現了某樣本既屬于集合HA，同時屬于HB的悖論。

例1:某種元件的壽命X（以小時計）服從正態分布N（μ，σ2），μ，σ2未知。現測得16只元件壽命如下：159，280，101，212，224，379，179，264，222，362，168，250，149，260，485，170，問是否有理由認為元件的平均壽命大于225（小時）？

HA：原假設H0：μ≤225H1：μ＞225，則H0的拒絕域為，現 有 n=16,α =0.05,查 表 得t0.05(15)=1.7531,計 算 得xˉ=241.5 ，s=98.73 ，故 有t=0.6685＜1.7531，t值沒有落在拒絕域中，即認為元件平均壽命都不大于225小時。

HB：建立假設H0：μ≥225H1：μ＜225，則H0的拒絕域為

故有t=0.6685＞-1.7531，t值沒有落在拒絕域中，即認為元件平均壽命都不小于225小時。綜合HA、HB的結論,二者唯一的交集是μ=225。但是這是一個在實際中幾乎不可能的結果，可以認為兩個結論是相反的。對立命題都能通過檢驗而被接受時，T檢驗似乎失去了判斷真偽的能力，這時T檢驗失效了。

2 T假設檢驗失效的原因分析

假設檢驗的理論基礎，是小概率事件的實際不可能性原理，即概率很小的隨機事件在個別的實驗中是不可能發生的。在假設檢驗的操作中，我們選取事件“當H0為真時拒絕H0”，并計算其發生概率（p值）。這是一個小概率事件。通過選擇顯著性水平α，設定“小概率”的標準。當p＜α時，小概率事件在一次抽樣中發生，違背了實際不可能性，認為應當拒絕H0從而接受H1。反之，則不違背小概率事件原理，不能拒絕H0。

不難看出，p值度量的是H0為真時，某個極不容易發生的事件的發生概率，換言之，p值度量的是不利于原假設的證據強度。p值越小，越反對H0，p值足夠小時（p＜α），即可推翻原假設。根據小概率事件的原理，我們根據p值拒絕h0是有相當大把握的。也就是說對于簡單原假設，只要參數假設值不完全等于真值，那么通過增大樣本容量，總是可以拒絕包含“相等”意義的原假設。

但是如果p值還沒有小到可以拒絕H0的水平，則沒有理由反對H0。但是否就是有充分理由接受H0呢？答案是否定的。H0是我們正在求證的總體效應，T檢驗則不能提供這個總體效應到底有多大或多重要的信息。因此我們只能說，不能拒絕H0。如例1，不拒絕H0：μ≤225和不拒絕H1：μ＞225，是不矛盾的。不拒絕并不意味著接受。實際上在假設H0實際上為真時，我們可能犯拒絕H0的錯誤，這被稱為“棄真”錯誤，也叫第一類錯誤（α值）。又當H0實際上不真時，我們也有可能接受H0，這類錯誤被稱為第二類錯誤（β值），又叫“取偽”錯誤。兩類錯誤產生的根本原因是抽樣。樣本只是總體的一部分，因此可能的樣本不止一個，而抽到的樣本具有很大的偶然性。用局部數據作為總體數據的估計不可能完全正確，基于此估計而作的檢驗產生錯誤的可能也就不可避免。

T檢驗的一個重大不足就是不能度量第二類錯誤（β值）的大小，但是希望它越小越好。但是在樣本容量固定的情況下，若減少犯第一類錯誤的概率，則犯第二類錯誤的概率往往增大。要使兩類錯誤的概率都減小，則必須增大樣本容量。那么什么情況下H0能被接受呢？由于接受域的中心是參數真值，故只有當假設值θ0完全等于真值θ，才能使無論樣本量多大，H0可以總能被接受。而這是不現實的。

實際中使用T檢驗去研究一個總體參數θ，都存在一個任意小的正數ε，使得當 ||θ-θ0＜ε時，可視為θ=θ0，(θ-ε,θ+ε)稱為θ的無差別區域。不斷增大的樣本會將θ與θ0之間的微小差別顯現出來（通過不斷減小的p值），并以p值為據，否定θ=θ0的原假設。檢驗本身并沒有錯，因為θ的確不是恰好就是θ0,但是如此“敏感”地找出應用中可忽略的差別，就沒有使用上的重要性了。無差別區域的存在，要求樣本容量必須具有上限。而控制第二類錯誤（β值）則要求樣本容量具有下限。二者對樣本容量的反向要求可能導致檢驗故障，因此必須在二者之間找到平衡，以達到檢驗的目標。

3 T檢驗失效的處理

3.1 原假設的選擇原則

假設檢驗的兩個結論在邏輯上可以共存，但是在實際中，得到一個如此模糊的判斷是沒有意義的。我們需要的是“接受H0”或“接受H1”這樣明確的論斷，來指導行動。也就是說，只能在HA或HB中選擇其一執行假設檢驗。這表明，兩個相反的假設檢驗中，應當有一種形式更符合現實的狀況，而能被直接采用。這就涉及到原假設的選擇原則。

仍以例1分析，如果做檢驗的是該電子元件的買方，根據自己的使用經驗或廠家信譽，認為元件的平均壽命不超過225小時，只有非常有利于生產方的觀察結果，才能改變對元件壽命的消極看法，于是就會提出H0：μ≤225作為原假設。同樣，如果買方相信元件平均壽命不小于225小時，沒有非常充分的理由，不應改變對廠方的信任，就會以H0：μ≥225為原假設。看上去原假設的選擇完全取決于檢驗者的個人意志，不夠嚴謹，但是，這種意志包含符合檢驗者地位的背景信息，根據這種個人意志選擇原假設而得出的結論，確定是有實用價值的。

據此探討原假設的選擇原則。假設檢驗的原理決定了H0一旦確定，接下來就是通過抽樣顯示的信息，來計算其作為原假設的反證據的強度。因此，原假設無疑處于被懷疑的地位。同時，由于小概率事件的實際不可能性，一次抽樣拒絕H0的可能性（α）大大小于接受的可能性（1-α），因此，原假設又是處于被保護地位的。通常我們采用的假設檢驗是顯著性檢驗，它是通過對α的設定控制第一類錯誤（棄真錯誤），而不考慮第二類錯誤的概率，但我們希望“取偽”的概率越低越好，這一點也要加以考慮。因此，根據原假設上述三個性質，可以得出建立原假設的三個基本原則：

①將研究者想收集證據予以反對的命題作為原假設。

②對于某些存在有改進、更新的問題的檢驗內容，出于謹慎考慮，應將已存在的狀態作為原假設H0，而將新改進反映在備選假設H1中。

③所有假設檢驗都可能犯兩類錯誤，但有些假設檢驗犯兩類錯誤所導致的后果的嚴重程度差別很大，則根據原假設的保護原則，將可能造成嚴重后果的錯誤設置為第一類錯誤，使之處于檢驗者控制下，而將其對應命題作為原假設H0。如：新藥的毒副作用檢驗中有兩種可能錯誤：a新藥有毒，而誤認為無毒；b新藥無毒，而誤認為有毒。顯然錯誤a比b后果嚴重，因其可能危害用藥者生命健康。因此將a設為第一類錯誤。則建立假設：H0：新藥有毒，H1：新藥無毒，則H0為真時拒絕H0的“棄真”錯誤，此處為“新藥有毒而認為其無毒”錯誤，通過顯著性水平α的選擇，使其發生概率小到可接受的范圍內。

3.2 樣本容量的控制

大樣本有可能帶來檢驗的失真（實際意義而非理論意義上的），那么恰當確定樣本容量就可以成為避免失效的手段。

（1）抽樣過程中樣本容量的控制

假設檢驗的操作過程大致可分為兩階段：第一階段是分析研究，建立原假設和備擇假設。這個階段可能要使抽樣調查，即通過抽取樣本處理之后，獲取對總體參數的估計等資料。理論上這不屬于假設檢驗，但是假設檢驗的前提。因為要判斷“θ=θ0”的命題，確定θ0不能是無根無據的。如果沒有可資利用的材料（例如經驗值和對參數的說明），就需要先抽樣估計進行確定。為保證估計的精度，抽樣估計中樣本量的確定有一整套技術手段。雖然仍不免誤差，但是可信度較高，可以視為真值。假設檢驗通常是在調查之后再抽取其他部分，就是驗證其是否與調查結論一致。調查是前探型的，檢驗是回溯型的。一般地，檢驗的樣本量小于調查的樣本量，此時不會出現檢驗失效。故得出T檢驗樣本容量上限確定的一個方法：在抽樣調查確定的n1和功效干預確定的n2中，若n1≤n2，則取n1為樣本容量，即樣本上限不超過抽樣調查的樣本量。

（2）功效干預

對于不需通過抽樣調查的T檢驗，如果所得的樣本容量不超過30，可以直接采用。其微小的干擾效應也不容易表現出來。

如果樣本容量超過30，可以采用功效控制法來確定樣本量。n＞30，T分布趨近于標準正態分布，故可記Ft≈Φ(x)。

對于均值的檢驗，可建立H0:μ=μ0，H1:μ≠μ0，顯著性水平為α，為避免T檢驗的失效，希望對于μ∈(μ0-ε,μ0+ε)，拒絕H0的概率(α′)也較小，顯然α′＞α，令α′=kα(k≥1)，而接受H0的概率為β(μ)≥1-α′。

已知

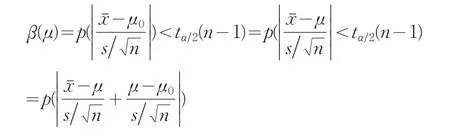
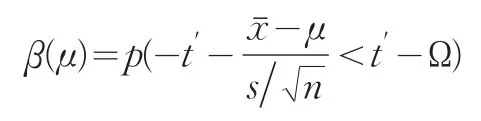
因Ft≈Φ(x)，而相應分位點亦逼近，故記t′≈μ′

故β(μ)=1-α+Φ(-μ′)-Φ(-μ′-Ω)-Φ(μ′)+Φ(μ′-Ω)=1-α+1- Φ(μ′)-1+ Φ(μ′+ Ω)-[Φ(μ′)- Φ(μ′- Ω)]利用拉格郎日中值定理，得β(μ)=1-α+Ω[Φ′(ζ2)-Φ′(ζ1)]=1-α+ Ω(ζ2-ζ1)Φ″(ζ3)]

其中，ζ1∈(μ′,μ′+Ω),ζ2∈(μ′- Ω,μ′),ζ3∈(ζ1,ζ2)

Φ″(x)=，當x=1時，有最大值，又ζ2-ζ1＜ 2Ω ，

所以：β(μ)≥1-α-又μ∈(μ0-ε,μ0+ε),因此：，對于α′=Kα(k≥1)，使β(μ)≥1-α′=1-α-(k-1)α成立則要求1)α，即此時，檢驗失效的情況應當不會出現。

（3）樣本容量的最終確定

①μ=μ0時：1-β（μ）≤α；②μ∈（μ0-ε，μ0+ε）時：1-β（μ）≤α′；③ ||μ-μ0≥δ時β（μ）≤β。可以好地實現控制兩類錯誤及避免檢驗失效的目標。

4 結論

通過以上分析，可以發現利用控制樣本容量可以控制t檢驗的失效。在進行T檢驗時：首先，利用公式-1)α確定樣本容量的上限，使β（μ）降低；其次，根據研究對象的特點確定正確的樣本容量，原則是盡可能的接近其上限值；第三：若要提高H0接受概率，即降低其被拒絕的概率，可以降低K值。第四，在T檢驗的實驗中，結合方差分析、相關分析等方法，作為T檢驗結論的監控和修正,通過參照對比，發現不同種方法結論的差異，避免由于單獨使用T檢驗而有可能產生的失誤。

[1] 盛驟，謝式千，潘承毅.概率論與數理統計[M].北京：高等教育出版社，2001,(3).

[2] 戴維·S·穆爾，統計學的世界[M].北京：中信出版社，2003,(1).

[3] 張時民，配對t檢驗和相關分析中的誤區[J].江西醫學檢驗,2001,19(5).

[4] 韓志霞,張玲，P值檢驗和假設檢驗[J].邊疆經濟與文化,2006,(4).

[5] 馮士雍,倪加勛,鄒國華，抽樣調查理論與方法[M].北京：中國統計出版社,1998,(1).

[6] 沈恒范，概率論與數理統計教程（第四版），北京：高等教育出版社，2003,(4).