基于AIC方法的切換神經網絡模型設計

連 捷， 張 凱

（大連理工大學 電子信息與電氣工程學部，遼寧 大連 116024）

0 引 言

混雜系統由于其在實際工程中的廣泛應用而得到深入研究.切換系統作為一類特殊的混雜動態系統，由一組連續（或離散）時間子系統和一條決定子系統之間如何切換的切換規則組成，整個切換系統的運行情況受控于這條切換規則.對于切換系統的研究近些年已經出現了大量的成果[1～3]，包括穩定性、能控性、能觀測性、控制器綜合等.

神經網絡由于其特有的結構與特點，早已成為很多學者重點研究的方向.又由于集成神經網絡和切換神經網絡的出現，神經網絡的研究進入了嶄新的階段.1990年Hansen等[4]開創性地提出了神經網絡集成方法，并證明通過簡單地結合神經網絡模型就可以顯著地提高模型泛化能力.近年來集成神經網絡模型被廣泛應用于各個領域，許多學者也根據不同的應用情況，針對集成網絡模型的逼近精度和泛化性能進行改進[5～10].在文獻[11]中作者對多種集成神經網絡做出了評價和比較.提出對神經網絡集成實現方法的研究主要集中在兩個方面，即怎樣將多個神經網絡的輸出結果進行結合以及如何生成集成中的個體網絡.2005年Huang等[12]首次將切換的思想引入神經網絡模型中，提出了切換Hopfield網絡模型，并給出了網絡在任意切換下穩定的條件.此后，一些學者將此設計思想應用于其他網絡[13、14]，也對其切換穩定性進行了分析證明.

本文主要工作是將切換思想與前向神經網絡結合，構造切換神經網絡模型；利用模糊C均值（FCM）聚類方法和赤池信息準則（AIC）將訓練數據分類并為模型建立切換規則.

1 切換神經網絡模型結構

基于AIC方法的切換神經網絡模型（AICSNN）如圖1所示，它由多個神經網絡和一條切換規則構成.各個子網絡訓練結束后，制定相應的切換規則，此后模型的運行方式由切換規則決定.

圖1 切換神經網絡模型Fig.1 The model of switched neural networks

在對每個神經網絡訓練之前要對訓練數據進行聚類處理.在一些設計中，通常會選擇K均值聚類，聚類后再利用每一類的數據訓練神經網絡.K均值聚類是將數據硬性劃分到某一類中，使用這種分類方法的缺點是在結束訓練后，網絡在每類數據邊緣處的輸出達不到很高的逼近精度.盡管各個網絡加權求和輸出有可能減小誤差，但是在邊界處過大的誤差也會使權值的確定出現偏差.本文使用FCM聚類方法對輸入數據進行聚類.FCM聚類方法是將數據劃分為n類，每個數據點用0～1的數表示屬于各個類的程度.與引入模糊劃分相適應，隸屬度矩陣U中的元素取值范圍為（0，1），并且各數據集的隸屬度的和等于1.

式中：n為類別數；c為分類樣本數；uij表示第i個樣本屬于第j類的隸屬度.通過確定歸為某一類的隸屬度就可以將數據進行分類，各類之間可以有重疊，所以利用FCM聚類方法對樣本數據分類可以解決K均值聚類導致邊緣精度下降的問題，而且FCM聚類方法還可以增加每類訓練數據的個數，提高網絡訓練精度.

2 切換規則設計

本文根據隸屬度與切換網絡訓練誤差的關系設計切換規則.

2.1 隸屬度與網絡訓練誤差的關系

在訓練數據分類時首先要確定數據點歸為某一類的隸屬度，以作為數據分類的標準，即當數據對于某一類的隸屬度大于時，則將數據歸為此類.假設類別數為n，則一定要小于1/n，以保證所有數據都能分到每一類中.分類結束后，分別使用每一類數據對相應的神經網絡進行訓練.為了更好地設計切換規則，下面將分析隸屬度與切換網絡訓練誤差的關系.

為了說明方便，將FCM聚類用圖2直觀地表示.圖中A統一表示非重疊部分，B統一表示重疊部分（圖2中只標出了兩兩重疊部分）.每一類數據訓練一個神經網絡，比較子網絡在不同區域的逼近精度.利用函數

作為測試函數，將A1中的訓練數據輸入其他子網絡，發現輸出誤差遠大于A1訓練數據對應的子網絡誤差.這一點也說明不同網絡通過不同區域數據訓練后，網絡性能也會在不同區域有著明顯的差別.因此在非重疊區域可以用隸屬度確定需要運行的子網絡.

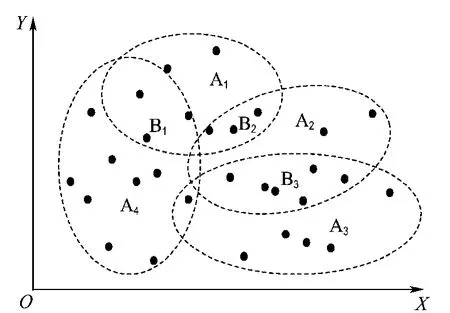
圖2 FCM聚類示意圖Fig.2 FCM clustering diagram

Bi（i＝1，2，3）區域為重疊區域，選擇某一 Bi區域進行仿真，分析隸屬度與訓練誤差的關系.圖3為隸屬度與誤差的曲線圖，x為Bi區域數據，e1（x）、e2（x）分別為x利用子網絡1和2測試時產生的誤差，u1（x）、u2（x）分別為x屬于分類組1和2的隸屬度，為了方便表示，將隸屬度的值除以40.從圖中可以看出重疊區域誤差與隸屬度沒有固定的關系，說明在此區域子網絡是否被激活不能由隸屬度確定.因此在重疊區域本文選擇應用網絡加權求和輸出的形式對目標函數進行逼近.

圖3 隸屬度與誤差曲線Fig.3 The curves of membership and error

2.2 隱層節點和輸出權值確定

AIC方法由Akaike提出，是從一類競爭模型中確定一個最佳模型的信息標準，它可以改善由網絡復雜導致的過擬合現象.本文使用AIC方法[12]確定隱層節點數，并在重疊區域通過AIC的值確定子網絡的輸出權值，以提高重疊區域網絡逼近精度.

單一網絡的性能與隱層節點的數目有很大的聯系，過少的隱層節點會使網絡逼近精度達不到要求，過多的隱層節點又會導致過擬合.所以選擇合適的隱層節點數有助于改善網絡的性能.在確定隱層節點數時需要同時考慮測試數據均方誤差和AIC值，相對較小的測試數據均方誤差值和AIC值對應的隱層節點數即為所選.

AIC值可通過下式計算：

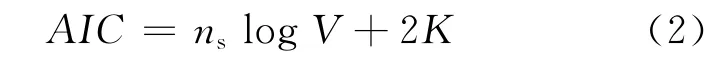
其中Ni為神經網絡輸入節點個數，Nh為隱層節點個數，No為輸出節點個數，NiNh＋NhNo即為所有權值個數，Nh＋No即為所有閾值個數.

利用AIC方法確定重疊區域子網絡的輸出權值.用分類后的數據計算出每一類的AIC值，用Δj表示各子網絡與最優網絡AIC值之間的差異，Δj＝AICj－minAIC，minAIC表示所有網絡計算AIC值中最優的.定義

其中β值用來決定Δm的范圍，小的β值表示每個Δm差別不大，大的β值表示每個Δm有較大差別，這里β值由下式確定：

Divi＝為第i個網絡的輸出值為網絡輸出的平均值.由以上這些計算結果確定權值為

其中wi為第i個神經網絡輸出的權值.

2.3 設計切換規則

根據上面的分析，設計相應的切換規則，盡量使每個子網絡在最優的區域工作.

假設訓練數據被分為n類，聚類中心為C＝（c1c2…cn），ci為第i類聚類中心.有m組測試數據X＝（x1x2…xm），按照下式計算測試數據與每一類的隸屬度：

其中vij表示第i個測試數據與第j個聚類中心的隸屬度.

切換網絡的輸出為

式中：σ（xi）＝ ｛j｜vij＞，j＝1，2，…，n｝，為當輸入數據為xi時的切換規則；σz∈σ（xi）表示σz為σ（xi）集合中的元素；fσz（xi）為被激活子網絡輸出；wσz為激活網絡對應權值，通過AIC方法確定，且

從切換規則的形式可以看出，不同的輸入數據經過切換規則后會激活不同的子網絡，同時會計算出激活網絡對應的輸出權值.當輸入數據在非重疊區域時，σ（xi）中僅有一個元素，表示此時僅有一個網絡被激活，相應的輸出權值wσz＝1.當輸入數據在重疊區域時，σ（xi）中會有多個元素，表示有多個子網絡被激活，切換規則會根據此時激活的子網絡計算出對應的輸出權值，切換網絡輸出Y由σ（xi）中所有元素對應的子網絡輸出加權求和得到.

3 切換神經網絡仿真

仿真1 選擇Matlab中的peak函數進行仿真測試，peak函數形式為

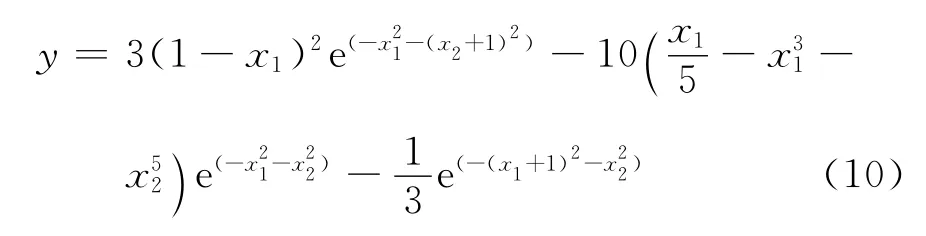
在peak函數中加入均值為0、方差為0.05的噪聲，選擇121組數據（x1，x2）作為訓練數據，其中x1，x2∈[－3，3].另外生成100組數據（x1，x2）作為測試數據用來測試網絡性能.采用FCM方法將訓練數據分為4類，對每一部分建立子網絡模型，選擇網絡模型為BP網絡，利用AIC方法選擇隱層節點數為15.每個子網絡訓練30次.網絡訓練完成后，根據訓練數據隸屬度按照AIC方法生成切換規則，最后利用測試數據對網絡進行測試.

將基于AIC方法的切換神經網絡模型（AICSNN）與單一網絡模型和基于AIC方法的集成神經網絡模型（AIC－ENN）進行比較，表1列出了各模型均方誤差（MSE）在最小值、平均值和標準差三方面的比較結果，表中數據為進行20次仿真后的計算結果.圖4給出了測試數據經過AIC－SNN模型仿真后與期望值的比較結果（yp為期望值，ya為實際值）.

表1 模型比較結果（仿真1）Tab.1 The comparison result of different models（Simulation 1）

圖4 AIC－SNN對于測試數據的仿真結果（仿真1）Fig.4 The simulation results of AIC－SNN for the test data（Simulation 1）

從表1可以看出基于AIC方法的集成神經網絡模型在逼近準確性方面要比其他兩種模型效果好.圖4中數據點都在傾斜角為45°的直線附近分布，這也說明了測試數據經過AIC－SNN模型仿真后，實際值較好地逼近了期望值.

仿真2 選擇Friedman＃1數據集作為仿真對象，數據集根據下式產生：

每個輸入向量含有5個分量，其中xi（i＝1，2，…，5）是0～1的隨機數，選取200組數據作為訓練數據，在訓練數據中加入均值為0、方差為1的高斯噪聲.選取不含噪聲的200個數據用來測試網絡性能.采用FCM方法將訓練數據分為4類，對于每一部分建立子網絡模型，利用AIC方法選擇隱層節點數，子網絡選用隱層節點為10的BP網絡，每個子網絡訓練30次.網絡訓練完成后，根據訓練數據隸屬度按照AIC方法生成切換規則，最后利用測試數據對網絡進行測試.

表2給出了各模型均方誤差的比較結果，表中的數據為進行20次仿真后的平均值.圖5給出了測試數據經過AIC－SNN模型仿真后與期望值的比較結果.

表2 模型比較結果（仿真2）Tab.2 The comparison result of different models（Simulation 2）

從表2可以看出，AIC－SNN模型無論在訓練數據準確性還是測試數據準確性方面都比AICENN模型效果好.圖5中數據點的分布情況也說明了測試數據經過AIC－SNN模型仿真后，實際值較好地逼近了期望值.

圖5 AIC－SNN對于測試數據的仿真結果（仿真2）Fig.5 The simulation results of AIC－SNN for the test data（Simulation 2）

仿真3 利用UCI數據集中的Servo數據進行仿真.該數據有167組，每組數據有4個類別屬性.利用130組數據作為訓練數據，37組數據作為測試數據.利用AIC方法選擇隱層節點數為15的BP網絡，每個子網絡訓練30次.網絡訓練完成后，根據訓練數據隸屬度按照AIC方法生成切換規則，最后利用測試數據對網絡進行測試.

表3為各模型均方誤差的比較結果，表中的數據為進行20次仿真后的平均值.圖6給出了測試數據經過AIC－SNN模型仿真后與期望值的比較結果.

從表3可以看出，AIC－SNN訓練數據均方誤差在三方面比較中都優于前兩個模型，測試數據均方誤差除了最小值稍高于AIC－ENN模型外，平均值和標準差都要優于前兩個模型，說明AICSNN模型有較好的逼近精度，較前兩個模型還是有一定的改善.從圖6也可以看出實際值較好地逼近了期望值.

表3 模型比較結果（仿真3）Tab.3 The comparison result of different models（Simulation 3）

圖6 AIC－SNN對于測試數據的仿真結果（仿真3）Fig.6 The simulation results of AIC－SNN for the test data（Simulation 3）

4 結 論

本文構建了切換神經網絡模型，利用FCM聚類方法和AIC方法為模型建立了切換規則.將數據分區域考慮，盡量應用子神經網絡訓練效果好的區域，增強了網絡的逼近能力.由于切換規則的使用，更好地利用了各個子網絡在特定區域具有較高逼近精度的特點，降低了模型工作復雜度，也改善了由于某些網絡訓練效果不佳帶來的輸出偏差.仿真結果表明，基于AIC的切換神經網絡模型不僅能降低訓練數據的誤差，而且能較好地降低測試誤差，使網絡有較好的逼近性能.但是，網絡中還有一些需要人為設定的參數，比如分類隸屬度和分類數目，所以還需進一步完善和深入研究.

[1] ZHAO Jun，HILL D J.On stability，and L2－gain andH∞control for switched systems[J].Automatica，2008，44（5）：1220－1232

[2] LIAN Jie，ZHAO Jun.Output feedback variable structure control for a class of uncertain switched systems[J].Asian Journal of Control，2009，11（1）：31－39

[3] 付主木，費樹岷，龍 飛.一類線性切換系統H∞狀態反饋控制：LM I方法[J].控制與決策，2006，21（2）：197－200

[4] HANSEN L K，SALAMON P.Neural network ensembles[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12（10）：993－1001

[5] ZHOU Zhi－hua， WU Jian－xin， TANG Wei.Ensembling neural networks：Many could be better than all[J].Artificial Intelligence，2002，137（1－2）：239－263

[6] SRIDHAR D V，SEAGRAVE R C，BARTLETT E B.Process modeling using stacked neural networks[J].AIChE Journal，1996，42（9）：2529－2539

[7] ISLAM M M， YAO Xin， MURASE K. A constructive algorithm for training cooperative neural network ensembles[J].IEEE Transactions on Neural Networks，2003，14（4）：820－834

[8] YU Lean， LAI Kin－keung， WANG Shou－yang.Multistage RBF neural network ensemble learning for exchange rates forecasting[J]. Neurocomputing，2008，71（16－18）：3295－3302

[9] ZHAO Zhi－ye，ZHANG Yun，LIAO Hong－jian.Design of ensemble neural network using the Akaike information criterion[J].Engineering Applications of Artificial Intelligence，2008，21（8）：1182－1188

[10] 熊智華，王 雄，徐用懋.一種利用多神經網絡結構建立非線性軟測量模型的方法[J].控制與決策，2000，15（2）：173－176

[11] 周志華，陳世福.神經網絡集成[J].計算機學報，2002，25（1）：1－8

[12] HUANG He， QU Yu－zhong， LI Han－xiong.Robust stability analysis of switched Hopfield neural networks with time－varying delay under uncertainty[J].Physics Letters A，2005，345（4－6）：345－354

[13] LI Ping，CAO Jin－de.Global stability in switched recurrent neural networks with time－varying delay via nonlinear measure[J].Nonlinear Dynamics，2007，49（1－2）：295－305

[14] LOU Xu－yang， CUI Bao－tong. Delay－dependent criteria for global robust periodicity of uncertain switched recurrent neural networks with timevarying delay [J].IEEE Transactions on Neural Networks，2008，19（4）：549－557