帶遞歸的模糊感知器有限收斂性

劉 燕， 楊 潔， 李 龍

（1.大連理工大學(xué) 數(shù)學(xué)科學(xué)學(xué)院，遼寧 大連 116024；2.大連工業(yè)大學(xué) 信息科學(xué)與工程學(xué)院，遼寧 大連 116034；3.衡陽師范學(xué)院 數(shù)學(xué)與計算科學(xué)系，湖南 衡陽 421008）

0 引 言

模糊邏輯和神經(jīng)網(wǎng)絡(luò)在信息處理系統(tǒng)中各有其優(yōu)缺點，最近，許多學(xué)者的工作都致力于將模糊系統(tǒng)與神經(jīng)網(wǎng)絡(luò)結(jié)合在一起，其中對模糊神經(jīng)網(wǎng)絡(luò)有很多的關(guān)注.文獻[1、2]提出了模糊感知器的一些學(xué)習算法；文獻[3]對0階Takagi－Sugeno推理系統(tǒng)的學(xué)習算法進行了收斂性證明；文獻[4、5]對多層模糊感知器進行了研究.

具有遞歸環(huán)節(jié)的動態(tài)模糊神經(jīng)網(wǎng)絡(luò)可以解決靜態(tài)網(wǎng)絡(luò)無法處理的暫態(tài)問題.FRNN（模糊遞歸神經(jīng)網(wǎng)絡(luò)）通過在網(wǎng)絡(luò)輸入層中加入遞歸連接，使網(wǎng)絡(luò)具有動態(tài)映射能力，從而對動態(tài)系統(tǒng)有更好的響應(yīng).

如果訓(xùn)練樣本線性可分，傳統(tǒng)的感知器算法能在有限步確定一個線性決策邊界，從而分離這兩類訓(xùn)練樣本[6、7].對于模糊感知器，文獻[8]提出了一種新的訓(xùn)練算法，并證明當樣本可分時，該算法有限收斂.那么，在模糊感知器中加入遞歸單元是否還能得到算法的收斂性？本文將對這個問題進行討論，給出若訓(xùn)練樣本模糊可分，在一定條件下，帶遞歸的模糊感知器算法有限收斂的結(jié)論及證明.證明過程的難點和關(guān)鍵在于確認遞歸項權(quán)值在學(xué)習過程中的單調(diào)遞減性.

1 帶遞歸的模糊感知器的結(jié)構(gòu)及梯度學(xué)習算法

1.1 帶遞歸的模糊感知器的結(jié)構(gòu)

本文研究的是具有n個外部模糊輸入單元、一個輸出單元和一個遞歸神經(jīng)元的感知器.其結(jié)構(gòu)如圖1所示，網(wǎng)絡(luò)的模糊訓(xùn)練樣本對為｛ξ（s），其 中是n維模糊輸入向量，O（s）是其理想輸出.

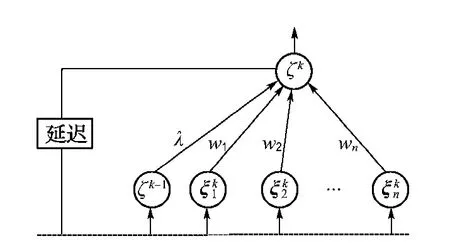
圖1 具有n－1－1結(jié)構(gòu)的遞歸模糊感知器的結(jié)構(gòu)Fig.1 The structure of recurrent fuzzy perceptron with n－1－1structure

將這些樣本隨機排列組成一個無窮序列｛ξk，其中每個樣本對｛ξ（s），O（s）｝出現(xiàn)無窮多次∈[0，1]n，為網(wǎng)絡(luò)在第k時刻的外部輸入向量，網(wǎng)絡(luò)第k時刻遞歸層的輸入

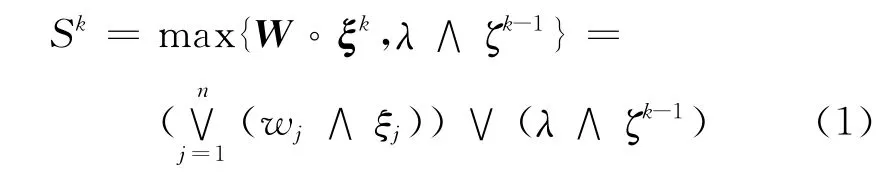
其中ζ0＝0，遞歸層的輸出為

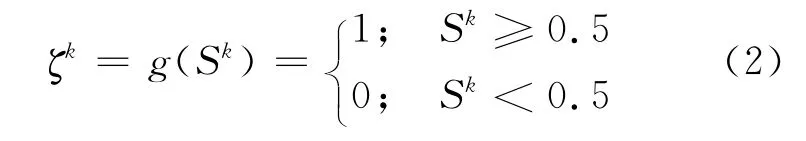
其中 ∨ 是取大運算；∧ 是取小運算；代表max－min（∨ －∧）合成算子；權(quán)重向量W ＝（w1w2… wn）T∈ [0，1]n，其中 wj（j＝1，2，…，n）代表連接第j個外部輸入神經(jīng)元和輸出神經(jīng)元的權(quán)值；連接遞歸神經(jīng)元和輸出神經(jīng)元的權(quán)值為λ，λ∈ [0，1].

網(wǎng)絡(luò)的訓(xùn)練目標是對給定的激活函數(shù)g（x）：R→｛0，1｝，確定權(quán)值（W，λ）∈ [0，1]n×[0，1]，使得訓(xùn)練樣本能夠被正確地分類，即ζ（ξ（s））－O（ξ（s））＝0.

為證明方便，記理想輸出為O（s）＝0的樣本為Xm，m＝1，2，…，M，1≤M＜S；另一些對應(yīng)理想輸出O（s）＝1的樣本，記為Yp，p＝1，2，…，P，1≤P＜S，M＋P＝S.定義兩個集合：ΦM＝｛1，2，…，M｝，ΦP＝ ｛1，2，…，P｝.

假設(shè)訓(xùn)練樣本可分，即存在一個模糊向量A＝（a1a2… an）T∈ [0，1]n使得

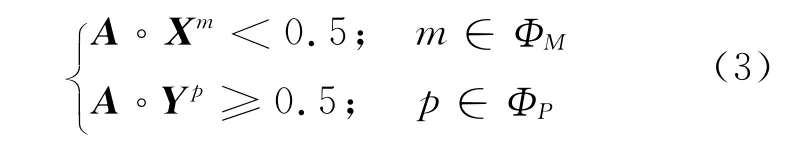
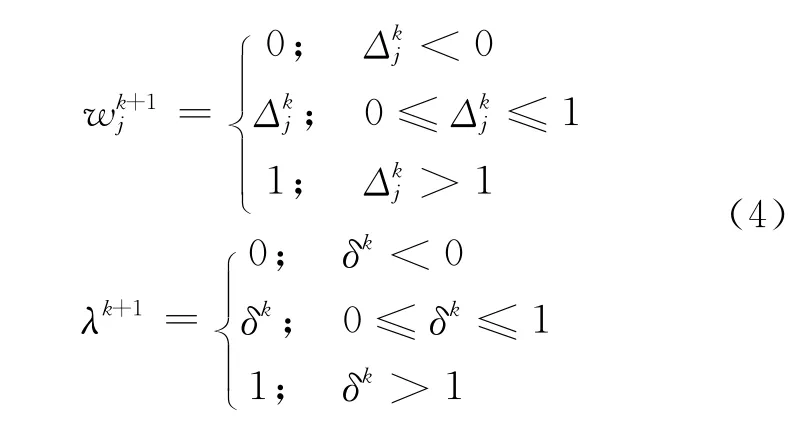
1.2 樣本集性質(zhì)

首先對訓(xùn)練樣本做一個假設(shè)[8].

假設(shè)Ⅰ 對任意一個m∈ΦM，至少存在一個m0，使得

下面給出模糊訓(xùn)練樣本對的3條重要性質(zhì)[8].

性質(zhì)1 對式（3）中模糊向量A，存在下標j1與j2，使得aj1≥0.5與aj2＜0.5分別成立.

基于性質(zhì)1，不失一般性，假設(shè)存在正整數(shù)q，1≤q＜n，使得a1，…，aq≥0.5，aq＋1，…，an＜0.5.

性質(zhì)3 對每一個Yp，p＝1，2，…，P，至少存在一個rp≤q，使得

接下來給出訓(xùn)練樣本的另一個假設(shè)[8].

假設(shè)Ⅱ 對任意一個j，R＜j≤n，至少存在一個mj，使得對每個1≤j≤q，至少存在一個pj，使得

2 有限收斂定理

在這一部分，分別給出迭代算法式（4）在n＝2和n＞2兩種情況下的收斂結(jié)果.

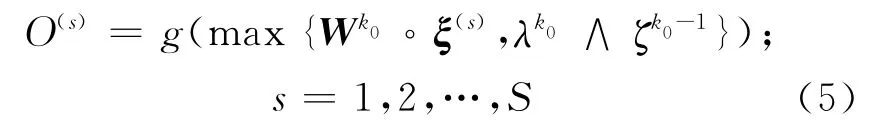
定理1 當n＝2時，若假設(shè)Ⅰ和Ⅱ成立，則算法式（4）有限收斂.

首先證明wk1＜0.5的情況下，權(quán)值的迭代不會停止.事實上，若wk1＜0.5且wk2≥0.5，那么對所有λk和ζk－1，都有

圖書館是全面系統(tǒng)地收藏著人類發(fā)展過程中所創(chuàng)造和積累的文獻信息資源集散地，又是人類文明、科技進步等的守護者與傳承者。文獻信息資源的傳播不受地域與時空限制，首先圖書館能夠把歷代學(xué)者所創(chuàng)造和積累的各種文獻信息載體保存下來，并傳遞給需要它的每位讀者，其次圖書館之間又能以開展的資源共享和館際互借等方式把不同地域的學(xué)者所創(chuàng)造的文化精神作品及時傳遞給需要它的需求者。圖書館以服務(wù)型社會理論為指導(dǎo),堅持”以人為本,讀者至上”人性化服務(wù)的原則,能夠在讀者的不同年齡階段，不同時間，滿足讀者不同層次的需求，讀者可以利用圖書館文獻資源各取所需，充分發(fā)揮自己的閱讀能力，開展自由自在的閱讀與研究活動，提高自身的綜合素養(yǎng)。

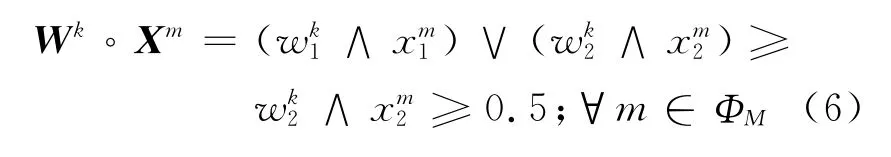
則

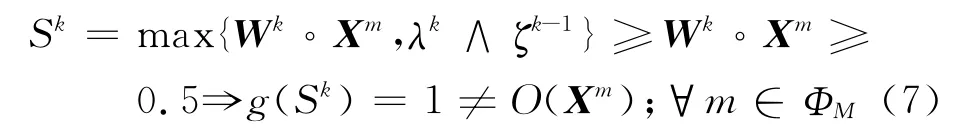
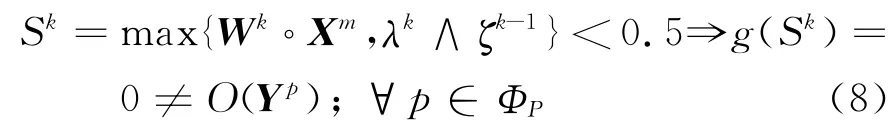
若λk≥0.5，有

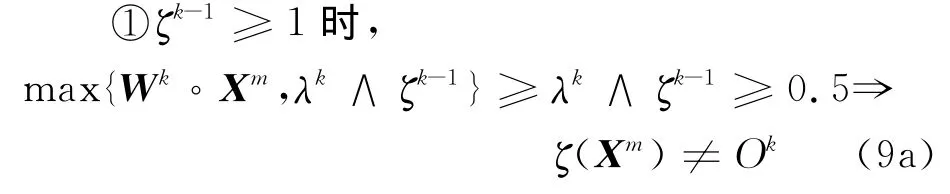
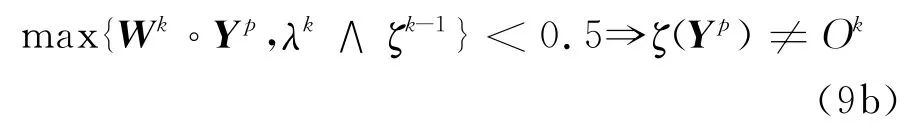
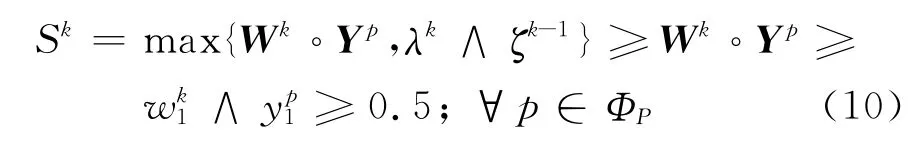
從而g（Sk）＝1＝O（Yp），p∈ΦP.由的單調(diào)不減性知，當k≥K1時，對｛（Wk，λk）｝真正起更新作用的只有因此，在無窮序列中除去

現(xiàn)在令k≥K1，若且λk＜0.5，則對ζk－1，（Wk，λk）滿足式（5），已是所求的解.否則，若對λk和ζk－1，有

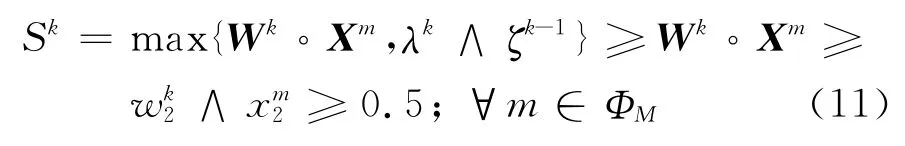
故ζ（SK）＝1≠O（Xm）.因此｛（Wk，λk）｝的迭代不會停止.

接下來，考慮n＞2的情況.為了保證收斂性，需要一些比較強的條件.

定理2 若假設(shè)Ⅰ和Ⅱ滿足，那么在以下條件成立時，算法式（4）有限收斂：

（a）存在一個r0，1≤r0≤q，使得p∈ΦP成立；

證明 由定理2條件（a）和性質(zhì)2，有η（Ok－，從而注意到當ξk沒被正確分類時，不等式嚴格成立.那么若達到0.5之前，（Wk，λk）滿足式（5），則算法式（4）有限收斂；否則，若，注意到其他權(quán)值的更新不影響的單調(diào)不減性，故在真正迭代有限步之后，會有即存在正整數(shù)K5，使得當k≥K5，有且WkYp≥

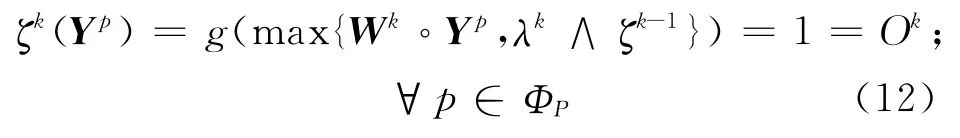
現(xiàn)令k≥K5，若wkj＜0.5，j＝R＋1，…，n，且λk＜0.5，則

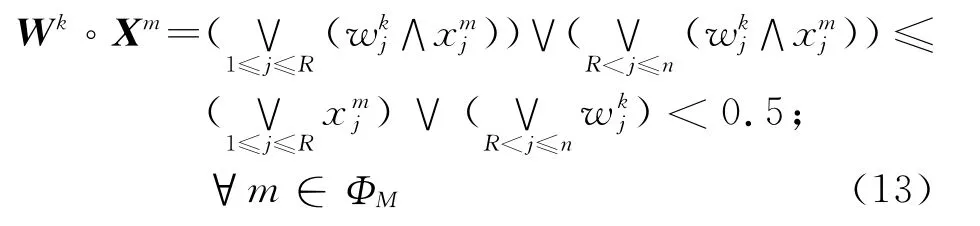
從而對ξk－1，都有Sk＝max｛WkXm，λk∧ζk－1｝＜0.5，那么式（5）成立，即（Wk，λk）已經(jīng)是所求的解.

若λk≥0.5，當ζk－1＝0時，仍有Sk＜0.5，從而式（5）成立；若ζk－1＝1，則

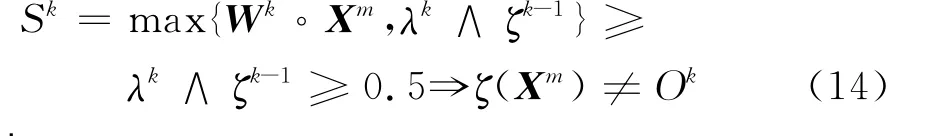
則

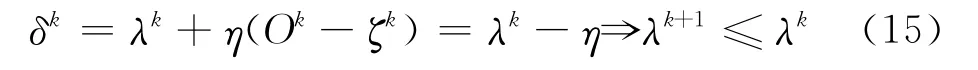
從而存在正整數(shù)K6，使得當k≥K6時，λk＜0.5.

說明（Wk，λk）不能將正確地分類，即使只有一個與ζk－1＝1）成立，式（5）就不成立，且有

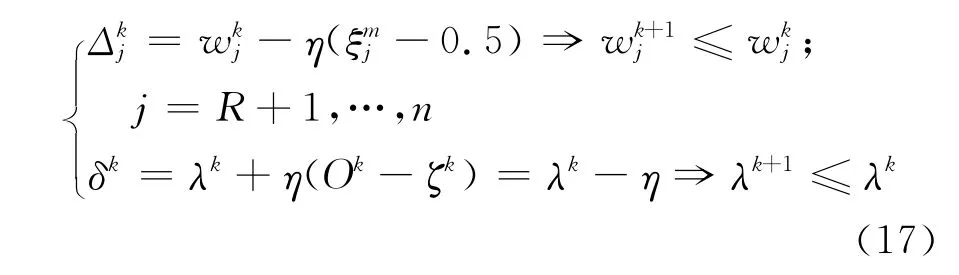
由定理2條件 （b），可 得η（Ok－ζk）（ξjm－0.5）≤0，R＜j≤n，故.結(jié)合假設(shè)Ⅱ，有成立，那么對每一個l＝

1，2，…，L，存在.因此，存在Kjl∈N，s.t.當成立.令則當1，…，n，此時式（5）成立，故算法式（4）有限收斂.證畢.

3 結(jié) 論

本文考慮的是帶遞歸的模糊感知器的有限收斂問題，其內(nèi)部運算基于max－min模糊邏輯運算，并且網(wǎng)絡(luò)結(jié)構(gòu)類似于內(nèi)部運算基于加法－乘法的傳統(tǒng)感知器.如果訓(xùn)練樣本線性可分，傳統(tǒng)的感知器算法能通過有限步的權(quán)值學(xué)習來分離屬于不同類別的訓(xùn)練樣本.本文拓廣了文獻[8]的結(jié)論，對遞歸模糊感知器學(xué)習算法的有限收斂性進行了探討.

1] LI L，YANG J，LIU Y，etal.Finite convergence of fuzzy delta rule for a fuzzy perceptron[J].Neural Network World，2008，18（6）：459－467

[2] CHEN J L，CHANG J Y.Fuzzy perceptron learning and its application to classifiers with numerical data and linguistic knowledge[J].IEEE Transactions on Fuzzy Systems，2000，8（6）：730－745

[3] WU W，LI L，YANG J，etal.A modified gradientbased neuro－fuzzy learning algorithm and its convergence [J]. Information Sciences， 2010，180（9）：1630－1642

[4] MITRA S，PAL S K.Fuzzy multi－layer perceptron，inferencing and rule generation [J]. IEEE Transactions on Neural Networks，1995，6（1）：51－63

[5] PAL S K，MITRA S.Multi－layer perceptron，fuzzy sets，and classification [J].IEEE Transactions on Neural Networks，1992，3（5）：683－697

[6] WU W，SHAO Z Q.Convergence of online gradient methods for continuous perceptrons with linearly separable training patterns[J].Applied Mathematics Letters，2003，16（7）：999－1002

[7] SHAO Z Q，WU W，YANG J.Finite convergence of on－line BP neural networks with linearly separable training patterns [J].Journal of Mathematical Research and Exposition，2006，26（3）：451－456

[8] YANG J，WU W，SHAO Z Q.A new training algorithm for a fuzzy perceptron and its convergence[C]//ISNN2005，Lecture Notes in Computer Science.Berlin：Springer，2005：609－614