小波神經網絡預測電價的新改進*

涂啟玉,張茂林

(云南電力調度中心,昆明 650011)

電力市場短期邊際電價預測是電力市場競價系統的重要組成部分,它為電力市場各交易方的競價策略提供了有效信息,對實現電力市場的利潤最大化意義重大。因此,高精確度、高智能化的短期電價預測已成為目前實際運行和理論研究中的熱點。

電價預測的方法大致可分為神經網絡法、統計學方法、模糊建模法、運行仿真法、市場均衡分析法及灰色理論和小波分析等數學方法。人工神經網絡法是個經久不衰的電價預測方法。它是由簡單的處理單元所組成的大量并行分布的處理機,這種處理機具有存儲和應用經驗知識的自然特性,它可通過學習過程從外部獲取知識,還能存儲獲取的知識信息[1]。一般主要采用BP神經網絡進行電價預測,但網絡存在收斂于局部極小點的缺點和神經網絡拓撲結構確定困難及全局搜索能力弱的問題[2]。

小波分析由于具有良好的時頻局部特性而被應用于BP神經網絡,從而加快其收斂速度,有效避免陷入局部最小值[3]。遺傳算法具有全局搜索能力強的特點[4],能夠用來對小波網絡的拓撲結構、權函數和伸縮平移因子進行優化訓練。因此,本文將二者應用于BP神經網絡,建立小波神經網絡預測電價模型,并用遺傳算法優化其結構和權重等參數,然后將其運用于邊際電價預測。

1 預測模型

1.1 基于BP網絡的預測模型

1.1.1 BP網絡結構[5]

本文采用一個3層BP神經網絡構建預測模型,在實際問題中一般輸入層與輸出層單元數由問題決定,隱含層層數在本文選取單隱含層,其單元節點數由試算確定。模型中每個神經元對應的傳遞函數為Sigmoid型函數,定義為

式中:n是神經元輸入;σ(n)為輸出。

利用BP網絡進行電價預測時可將影響邊際電價較大的幾種因素作為輸入,如預測負荷、反映供求關系的指標、歷史電價等,根據實際情況確定合適的隱含層單元數(試算求得),輸出層單元節點數本文由于輸出僅時段電價,故輸出層節點數為一。

1.1.2 基于BP網絡的電價預測模型

根據BP神經網絡的特點,基于BP神經網絡電價預測模型實現過程[5]包括:①輸入變量的選擇;②數據樣本大小的選擇及數據歸一化;③網絡結構的確定;④網絡的訓練與仿真。

1.1.3 BP網絡存在的缺陷

研究表明,簡單的BP網絡存在許多問題[6]:算法的學習收斂速度慢;易陷入局部最小值;網絡結構的選取,特別是隱含層節點數的選取過于經驗化,影響網絡的逼近能力及推廣性質;網絡參數(權值、閾值)確定一般未能達到最佳。

1.2 小波神經網絡預測模型

小波神經網絡[7]是基于小波分析而構成的人工神經網絡模型,即使用母小波取代傳統的Sigmoid函數,其函數描述是通過所選取的一簇母小波進行疊加實現的。如函數f(x)可用如下所示一簇母小波進行逼近:

設xi是輸入層的第i個輸入神經元,y是輸出層的輸出值,W ij是連接輸入層節點i與隱含層節點j的連接權值;θj是隱層節點j的閾值;W j1是隱含層j與輸出層(輸出層只有1個,即電價)的連接權值;θ是輸出層閾值;aj,bj分別是隱層節點j的伸縮和平移系數;M為輸入層節點數;N為隱層節點數。則上述模型的輸出可表示為

其預測流程見圖2所示。

圖1 BP網絡結構圖Fig.1 BP model structure

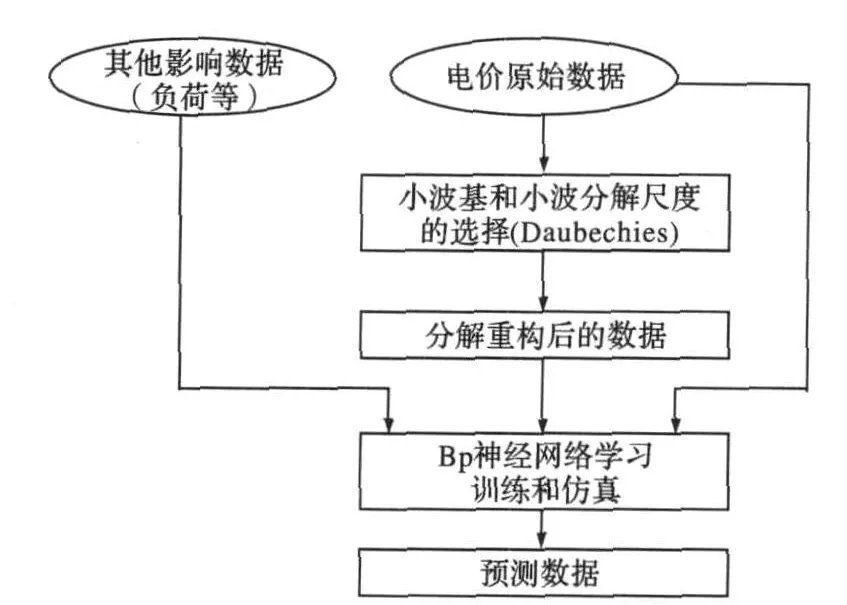
圖2 小波網絡預測模型流程圖Fig.2 Forecastingmodel of wavelet transformation and neural network

同神經網絡模型相比,小波神經網絡具有以下優點:①小波神經元的低相關性,使得小波網絡有更快的收斂速度;②隱層單元等于小波基數,由于它引入了2個新的參變量——伸縮因子和平移因子,從而使其具有更靈活有效的函數逼近能力;③當輸入信號樣本空間不均勻分布,即數據點在某些區域較密,而在另外一些區域稀疏時,小波神經元的良好局部特性和多分辨率學習可實現與信號良好匹配,小波能以不同分辨率表示函數特性,使得小波網絡有更高預報精度,在數據稠密區,以高分辨率學習,在稀疏區采用低分辨率學習,而單一分辨率的激勵函數對數據稠密不加區分。

1.3 基于遺傳算法的小波神經網絡

采用小波神經網絡對邊際電價進行預測的方法有一定的局限性[2,8]:主要是神經網絡拓撲結構難以確定,以及BP算法受到連接初始權值影響,容易陷入局部極值。

遺傳算法可以用于優化小波神經網絡的拓撲、結構和連接權學習過程,其優化流程如圖3所示。

采用遺傳算法優化小波網絡的具體步驟[9]:

1)結構及參數編碼,由于在本文中對網絡拓撲結構的優化,僅僅考慮對隱含層小波基個數優化(隱含層單元節點數),因此在初始化群體時,隨即產生N個網絡結構,每個結構中小波基個數采用實數制編碼,而對于神經網絡的各個權值,、閾值θ和隱層節點的伸縮平移算子也按次序編成一個字符串作為問題的一個解。

圖3 GA優化小波網絡流程圖Fig.3 Forecastingmodel optim ized by GA

2)輸入數據歸一化處理及小波神經網絡訓練后,計算適應度值。適應度函數計算公式如下:

f=C-e;

式中:C為一常數;e為誤差分別為第m個訓練樣本的第k個輸出節點的期望輸出與實際輸出;M為訓練樣本數;K為輸出節點數。

3)根據每個個體的適應度f,計算選擇概率在實際訓練中,一般將適應度最大的個體直接遺傳給下一代。

4)對當前群體進行交叉和變異。

5)從當前父代和子代的所有個體中選擇出n個適應度較大的個體構成下一代群體。然后再計算適應度值,開始新一輪迭代。終止條件為群體適應度趨于穩定或者誤差e小于某一給定值,或已達到預定的進化代數。

2 實例仿真

本文采用加州電力市場2000年3月1日至2000年3月31日24 h電價與負荷數據[10]進行模型的訓練仿真。表1是基于遺傳算法的小波神經網絡預測模型和BP神經網絡的模型參數。

表1 小波神經網絡預測模型參數Tab.1 M odel parameter

其中:

Pw(i-1,t),Pw(i-2,t),Pw(i-3,t),Pw(i-4,t),Pw(i-5,t),Pw(i-6,t)分別為預測時段前6日同時段分解重構電價;

P(i-1,t),P(i-2,t),P(i-3,t),P(i-4,t),P(i-5,t),P(i-6,t)分別為預測時段前6日同時段的時段電價;

L(i,t)為預測時段本日同時段負荷;

L(i-1,t),L(i-2,t),L(i-3,t),L(i-4,t),L(i-5,t),L(i-6,t)分別為預測時段前6日同時段的系統負荷;

P(i,t)為預測時段的時段電價。

圖4給出了分別應用神經網絡模型、小波神經網絡模型、遺傳算法優化的小波網絡模型預測的加州市場2000年4月1日24 h電價結果。表2表示三種預測方法的預測效果評價值,使用的評價指標有平均絕對百分比誤差MAPE(mean absolute percentage error)和預測標準差SDE(standard deviation error)[11],分別定義如下:

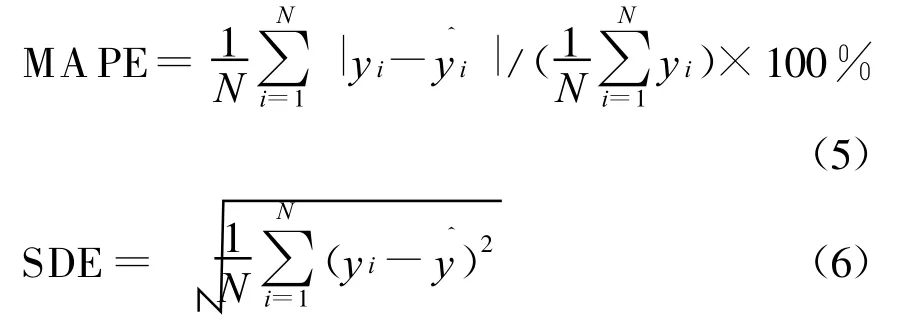
其中:yi為預測對象的實際值為預測值;N為預測對象的個數。

從圖4可以看出,基于小波分析的神經網絡和用遺傳算法優化的小波網絡預測的電價值較神經網絡的預測值,跟實際值擬合程度更高,且前兩者在波峰和波谷預測效果更高。表2更進一步說明小波神經網絡和基于遺傳算法的小波神經網絡的預測精度高于神經網絡模型,而基于遺傳算法的小波神經網絡模型精度較小波網絡有一定的提高。對于模型算法收斂效果的比較,由于神經網絡和小波神經網絡的隱含層節點數及各權重都是采用經驗隨機值,故在很多情況下,算法不能收斂,即使收斂其收斂速度也很慢且存在局部極值[7,12],而使用遺傳算法優化的小波神經網絡在運行中由于各參數權重都是優選的,其結果必然會收斂到一個預設的值,且收斂速度很快,這充分體現了用遺傳算法優化的小波神經網絡的先進性。

圖4 24小時實際和預測電價值Fig.4 24h actual and forecasting results

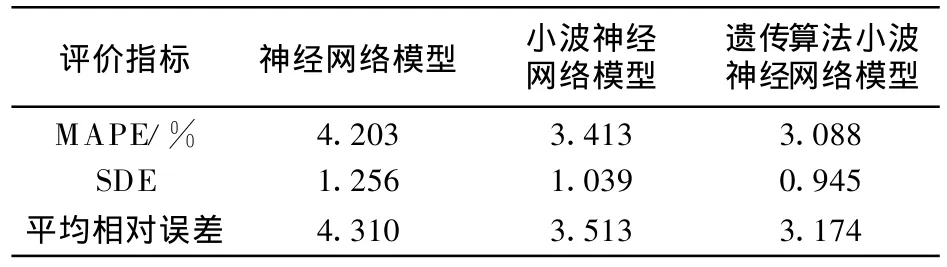
表2 三種預測方法的預測效果評價表Tab.2 Evaluation of forecasting resu lts

3 結語

本文針對邊際電價預測問題,采用預測效果較好的神經網絡模型,將小波分析與神經網絡結合起來建立小波神經網絡模型,在此基礎上用遺傳算法優化網絡拓撲結構和各權重系數。由于其結合了遺傳算法的全局優化搜索能力及小波變換良好的時頻局部性質,有效避免了普通BP神經網絡需人為給定網絡結構以及易陷入局部極小值的缺陷。經實例仿真,基于遺傳算法的小波神經網絡模型有效提高了預測精度,并且可使得求解問題迅速收斂。因此,本文所述的基于遺傳算法的小波神經網絡預測模型,在邊際電價預測中有很好應用前景。

[1] Zhang Li,Luh Peter B,Kasiviswanathan K rishnan.Energy clearing price prediction and confidence in terval estimation w ith cascaded neuralnetw orks[J].IEEE T rans on Power Systems,2003,18(1):99-105.

[2] 楊樸,游大海,謝培元(Yang Pu,You Dahai,X ie Peiyuan).基于遺傳算法和BP神經網絡的電價預測(Price forecasting based on genetic algorithm and BP neuralnetwork)[J].水電能源科學(W ater Resources and Power),2003,21(2):84-86.

[3] 楊波,趙遵廉,陳允平,等(Yang Bo,Zhao Zunlian,Chen Yunping,et al).基于小波變換的邊際電價神經網絡預測新模型(A novelMCP forecastingmodel based on wavelet transformation and neu ral network ensem ble in day-ahead market)[J].電力系統自動化(Autom ation of E-lectric Pow er Sy stem s),2007,31(12):40-44.

[4] 岑文輝,趙慶,戴文祥(Cen Wenhui,Zhao Qing,Dai Wenxiang).遺傳算法及在電網規劃中的應用(Genetic algorithm&itsapplication in power netw ork planning)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),1995,7(2):1-9.

[5] 劉正國,付祥明,高付英,等(Liu Zhengguo,Fu Xiangming,Gao Fuying,et a l).基于神經網絡的浙江發電市場清算電價預測方法(Forecasting market-clearing price in Zhejiang generation market using neu ral netw ork)[J].電力系統自動化(Autom ation of Electric Pow er Sy stems),2002,26(9):49-52.

[6] 周浩,文福栓,張富強,等.電力市場風險管理-建模分析與預防策略[M].杭州:浙江大學出版社,2006.

[7] 張大海,畢研秋,鄒貴彬,等(Zhang Dahai,Bi Yanqiu,Zou Guibin,et a l).小波神經網絡及其在電力負荷預測中應用概述(Overview of wavelet neural netw ork and itsapplication in pow er load forecasting)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),2004,16(4):11-15,26.

[8] 陳思杰(Chen Sijie).小波神經網絡在電力系統短期電價預測中的應用(The Wavelet Netwo rk Method Used for Shortterm Electricity Price Forecasting of the Pow er Systems)[D].杭州:浙江大學電氣工程學院(Zhejiang:School of E-lectrical Engineering,Zhejiang University),2006.

[9] 閻平凡,張長水.人工神經網絡與模擬進化計算[M].北京:清華大學出版社,1999.

[10]徐國祥.統計預測和決策[M].上海:上海財經大學出版社出版,2005.

[11]畢研秋,周文連,張大海,等(Bi Yanqiu,Zhou Wenlian,Zhang Dahai,et a l).連續小波神經網絡收斂性能的探討(Investigation on the convergenceperformance of con tinuous w avelet neu ral netwo rk)[J].電力系統及其自動化學報(P roceedings of the CSU-EPSA),2005,17(6):50-54.