馬爾科夫鏈在電力負荷組合預測中的應用*

李 敏,江 輝,黃銀華,宋小明

(湖南大學電氣與信息工程學院,長沙 410082)

電力負荷預測是電力系統安全、經濟運行的前提,是實現電網增容和改建的重要依據。負荷預測的準確性直接影響新機組的裝機容量、安裝位置和安裝時間。因此,高精確度的負荷預測是電網規劃的重要內容。

電力負荷預測受政策、經濟、環境等因素影響,是典型的復雜非線性問題。在多因素影響下,單一負荷預測很難準確描述電力負荷變化規律[1～3]。為合理考慮多種因素對電力負荷影響,文獻[4～6]提出組合預測模型。組合預測整體上優于單個預測,同時組合預測中變權重方法比固定權重更符合實際,預測結果更準確。但難點在于如何分配各種方法的權重。常見的權重處理方法[7]有最優組合和變權組合。最優組合預測可能出現沒意義的負權重,且權重可能不是最優;而變權重克服了最優組合的缺點,更加符合實際。但確定方法較復雜。

本文利用馬爾科夫鏈對篩選后各方法的狀態概率分布的變化規律進行擬合,將一步轉移概率矩陣的估計問題轉化為多元約束的自回歸模型,進而求解出一步轉移概率矩陣的最小二乘公式解。然后利用一步轉移概率矩陣的估計和初始狀態概率分布給出各方法的權重,并利用非負權重進行組合預測。仿真實例驗證了本方法的可行性和優越性。

1 馬爾科夫鏈基本原理

馬爾科夫[8,9]過程是具有無后效性的隨機過程。無后效性是指在已知“現在”的條件下,“將來”的狀態與“過去”的狀態無直接關系。時間和狀態都離散的馬爾科夫過程,為馬爾科夫鏈。

對離散空間E中的隨機序列{Xt,t=1,2,…},若對于任意的非負整數n,l,k及任意的非負整數及滿足:

則隨機序列{Xt,t=1,2,…}為馬爾科夫鏈。

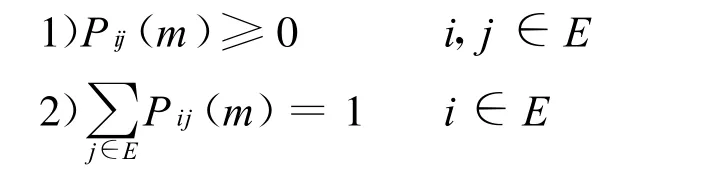
2 基于馬爾科夫鏈的組合預測

設yt為t時刻負荷觀測值(1≤t≤T)或預測真值(t＞T)(t=1,2,…),T為擬合時段,t=T+1,…為預測時段。假令有N種負荷預測方法,第i個預測方法對t時刻變量yt的擬合值(1≤t≤T)或預測值(t＞T)記為yti。當將yt看做是隨機變量時,yt1,yt2,…,ytN可將yt取值分為N個狀態,設:

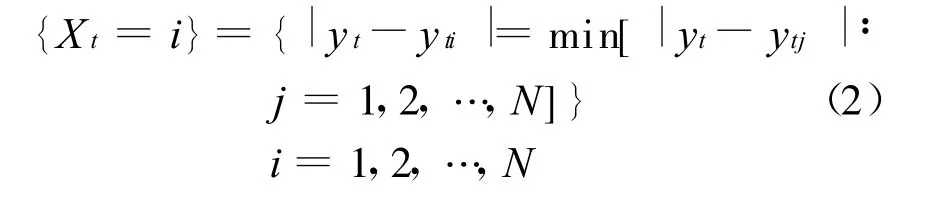
特別當

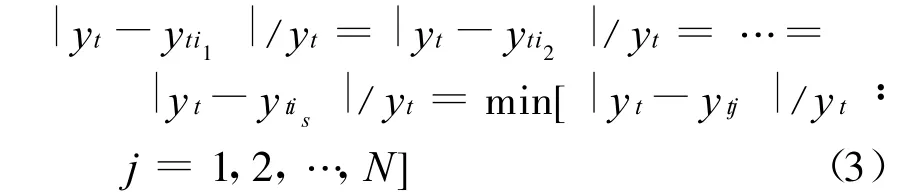
時,i={i1,i2,…,is};其中下標s(s≥1)表示滿足|yt-yti|/yt=min[|yt-ytj|/yt∶j=1,2,…,N]時的預測方法數。

用馬爾科夫鏈擬合隨機序列{X t∶t=1,2,…},狀態概率

則狀態概率分布為P t=[Pt1,Pt2,…,PtN]′。記P ti的估計值為,則:

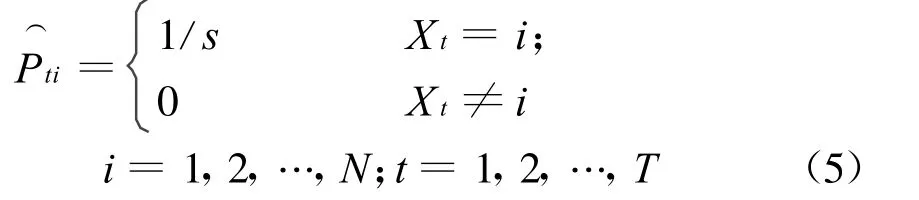
由此產生狀態概率分布的觀測值

設隨機序列{Xt∶t=1,2,…}的一步轉移概率矩陣為Q=[qij]N×N,設

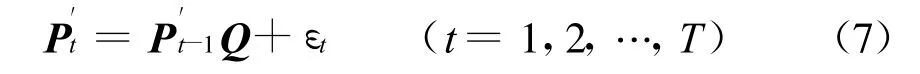
其中ε1,ε2,…,εT為隨機誤差向量。注意到Q應滿足b′Q′=b′,其中b′=(1,1,…,1)為一個N維行向量,則Q的估計問題化為如下約束多元自回歸模型對Q的估計問題

對于上式,可以證得[10]:若C′C可逆,則矩陣Q的最小二乘解為

E(ε′)的估計為

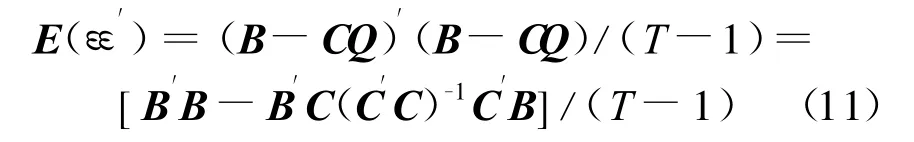
這樣可得狀態概率的預測公式為

3 多模型的自動篩選方法

負荷預測的數學模型都是理想抽象的。由于預測量發展變化規律的多樣性和復雜性,以及許多不確定因素的存在,單一預測模型的精度不可能在所有情況下都有較高的預測精度。因此,在進行組合預測之前,應對眾多單一預測模型進行判斷和篩選,舍棄那些效果明顯較差的模型,同時選出比較有效地模型,從而進一步提高組合預測的精度。

本文采用一種多模型自動篩選算法[11]對單一預測模型判斷篩選。該算法利用決策理論中的幾率矩陣(odds-matrix)來定量確定每種單一模型的權重,每種權重代表該方法的優劣性,通過權重概率分布函數判斷各預測模型的顯著性,從而篩選出符合特定地區、特定時期負荷特點的預測方法。

假設e種單一預測模型實際的優劣性用權重相量w={w1,w2,…,we}表示,權重越大,預測模型i越好。令O exe為決策矩陣,矩陣中的每一個元素Qij可以看作預測模型i優于j的幾率,則自動篩選算法可分為以下2個步驟:

1)應用決策理論中的odds-matrix方法評價各個單一方法,引入權重概率分布函數來描述各個方法的優劣性。根據每個單一預測模型的原始誤差,生成決策矩陣,獲取決策矩陣Oexe,并利用最小二乘法或特征向量法等方法求取權重相量w。

2)估計分布函數的數學期望,得到優越方法的集合。根據權重相量w及權重的數學期望EV對單一預測模型進行判斷篩選。當權重w i＞EV時,則預測方法參與組合預測,否則剔除該方法。

基于馬爾科夫鏈擬合的變權重組合預測的流程圖如圖1所示。

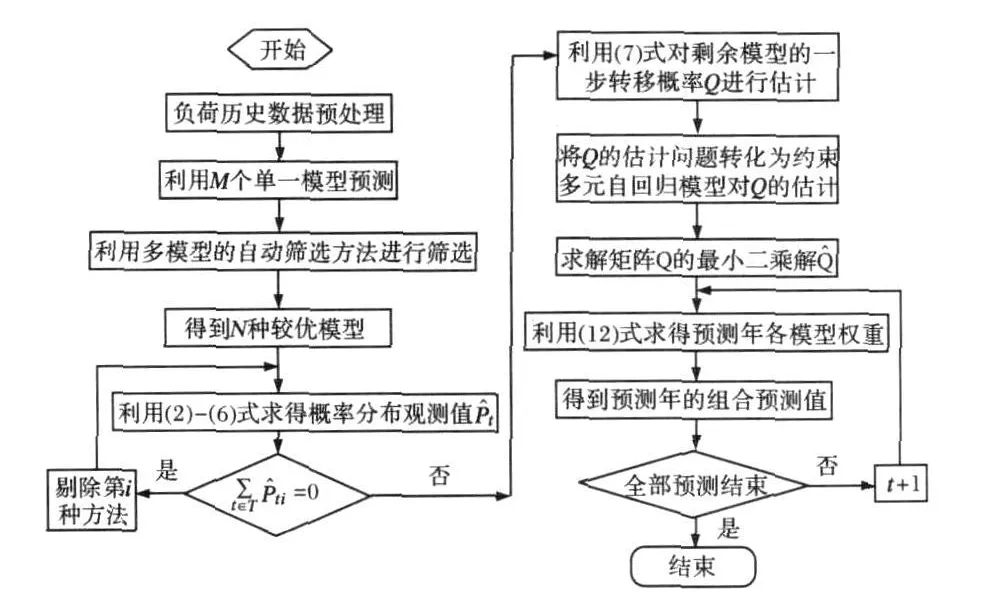
圖1 計算流程Fig.1 Flow chart of calcu lation

4 算例分析

采用文獻[12]中算例所提供的數據,將某地區1998～2005年全社會用電量作為樣本(見表1),利用1998～2002年數據,采用本文所提組合預測方法對2003～2005年該地區全社會用電量進行預測。

表1 1998-2005年用電量數據Tab.1 Electric energy consum ption from 1998 to2005

利用指數模型I、拋物線模型、灰色系統法、3次曲線模型、人工神經網絡、指數平滑法、模糊聚類識別預測法7個單一模型預測。根據單一模型預測結果,利用本文多模型自動篩選方法篩選,從中篩選出拋物線模型、3次曲線模型、灰色系統法3種單一模型。運用本文組合預測方法對2003～2005年該地區全社會用電量進行組合預測,得出3個模型權重值和組合預測值。表2為篩選出的三種方法負荷預測結果;表3為組合預測權重值和預測結果。

表2 3種模型的預測結果Tab.2 Results of three forecastingmodels

表4為本文預測方法和文獻[12]預測方法比較。由表4知,本文方法最小誤差為0.09%、最大誤差為0.25%,而文獻[12]預測方法的最小誤差為0.17%、最大誤差為0.8%。可見,本文預測方法較精確,在歷史數據與預測年越接近時預測越準確,2003年時,本方法誤差僅為0.09%。

表3 3種模型時變權重及組合預測結果Tab.3 Resu lts and weights of threemodels

表4 預測結果比較Tab.4 Comparison o f the forecasting resu lts

5 結語

本文以最小誤差為準則,利用馬爾科夫鏈擬合狀態概率分布的變化規律,并將一步轉移概率矩陣的估計問題轉化為多元約束自回歸模型,然后利用一步轉移概率陣的估計和初始狀態概率分布給出了狀態分布的變權重預測方法。實例表明,該方法推理簡單,不會出現負權重,具有實用性;同時,計算中還發現:所用歷史資料與待測預測年時間上越接近,則預測越準確。

[1] 李翔,高山,陳昊(Li Xiang,Gao Shan,Chen Hao).基于變結構協整理論的中長期電力負荷預測模型(A new medium-and long-term forecastingmodelbased on variab le structu re cointeg ration theory)[J].電網技術(Power System Technology),2007,31(9):48-52.

[2] 雷紹蘭,孫才新,周湶,等(Lei Shaolan,Sun Caixin,Zhou Quan,et a l).基于徑向基神經網絡和自適應神經模糊系統的電力短期負荷預測方法(Shortterm load forecasting method based on RBF neural network and ANFIS system)[J].中國電機工程學報(Proceedings o f the CSEE),2005,25(22):78-82.

[3] 陳澤淮,張堯,武志剛(Chen Zehuai,Zhang Yao,Wu Zhigang).RBF神經網絡在中長期負荷預測中的應用(Ap plication of RBF neural network in medium and long term load forecasting)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),2006,18(1):15-19.

[4] 肖先勇,葛嘉,何德勝(Xiao Xianyong,Ge Jia,He Desheng).基于支持向量機的中長期電力負荷組合預測(Combination method of m id-long term load forecasting based on support vec tor machine)[J].電力系統及其自動化學報(Proceedings of the CSUEPSA),2008,20(1):84-88.

[5] 李春生,王耀南(Li Chunsheng,Wang Yaonan).基于條件熵的電力負荷組合預測模型(Combinationmodel of load forecasting based on conditionalentropy)[J].電力系統及其自動化學報(Proceedings o f the CSUEPSA),2007,19(4):55-58.

[6] 游仕洪,程浩忠,謝宏,等(You Shihong,Cheng H aozhong,Xie Hong,et a l).模糊組合預測在中長期負荷預測中的應用(Application of combination forecasting by fuzzymethod in m id-and long-term load forecasting)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),2004,16(3):53-56,78.

[7] 余健明,燕飛,楊文宇,等(Yu Jianm ing,Yan Fei,Yang Wenyu,eta l).中長期電力負荷的變權重組合預測模型(G ray variab le w eight combination model for m iddle and long term load forecasting)[J].電網技術(Pow er System Technology),2005,29(17):56-60.

[8] 吳凱,林爭輝(W u Kai,Lin Zhenghui).馬氏鏈在集成電路功耗估計中的應用(Application o f Markov chain in VLSIpower estimation)[J].計算機工程(Computer Engineering),2003,29(13):162-164.

[9] 何鑫,宋平崗,官二勇(He Xin,Song Pinggang,Guan Eryong).用馬氏鏈方法預測全國年發電量趨勢(Forecasting the trend of electricity p roduction in the year future by using Markov chain)[J].華東交通大學學報(Journal of East China Jiaotong University),2006,23(4):51-54.

[10]張堯庭,方開泰.多元統計分析[M].北京:科學出版社,1982.

[11]高峰,康重慶,夏清,等(Gao Feng,Kang Chongqing,Xia Qing,et a l).負荷預測中多模型的自動篩選方法(Multi-model automatic sifting methodology in load forecasting)[J].電力系統自動化(Automation of Electric Power System s),2004,28(6):11-13,40.

[12]孫廣強,姚建剛,謝宇翔,等(Sun Guangqiang,Yao Jiangang,X ie Yuxiang,et al).基于新鮮度函數和預測有效度的模糊自適應變權重中長期電力負荷組合預測(Com bination fo recast of medium-and long-term load using fuzzy adaptive variab le weight based on fresh degree fun ction and forecasting availability)[J].電網技術(Power System Technology),2009,33(9):103-107.