DPWⅢ機翼和翼身組合體構型數值模擬

王運濤，王光學，張玉倫

(中國空氣動力研究與發展中心空氣動力學國家重點實驗室，四川 綿陽 621000)

0 引言

隨著大型專業前置處理軟件、計算流體力學(CFD)技術、后置處理軟件和計算機硬件技術的飛速發展，基于RANS方程(Reynolds Averaged Navier-Stokes)的CFD軟件已經可以模擬高度復雜飛行器外形的繞流流場［1］。市場競爭、安全性和商業利潤等多重的壓力，使得CFD成為現代飛行器成功設計的重要因素，已經與風洞試驗一道成為飛行器氣動設計的最重要的研究手段［2］。我國中長期科學和技術發展規劃綱要中，大飛機的研制已經被列為重大專項，在大飛機的氣動設計過程中，CFD必將發揮重要的作用。

盡管飛行器設計者已經充分意識到了CFD應用的巨大潛力，但CFD軟件尚沒有像計算結構力學(CSM)軟件那樣被認為是一個成熟的工具，原因主要包括流動控制方程中包含各種假設、計算效率和計算精度需要進一步提高、復雜外形的計算結果強烈依賴于使用者的經驗和網格質量等方面。因此，CFD軟件的驗證和確認問題(Verification＆Validation)依然是當前研究的熱點［3］。為研究CFD模擬的精準度問題，國際上先后開展了許多專題研究，如 ETMA(Efficient Turbulent Models for Aeronautics)、ECARP(European Computational Aerodynamics Research Project)、AVTAC(Advanced Viscous Flow Simulation Tools for Complete Civil Transport Aircraft Design)等，其中比較具有代表性是AIAA的DPW(Drag Prediction Workshop)系列會議。

針對運輸機構型，為研究CFD的阻力計算精度問題，明確CFD技術的現狀和未來的努力方向，AIAA阻力計算工作小組在2001年6月召開了第一次工作會議(DPW I)，該次會議選擇了DLR-F4翼身組合體作為標準算例，在本次會議上18家單位采用14中軟件提供了計算結果［4］，2003年6月召開了第二次工作會議(DPW II)，該次會議選擇了DLR-F6翼/身/掛/艙組合體作為算例，會議的重點是掛架/吊艙的安裝阻力，在本次會議上共有22家研究機構提供了20種CFD軟件的計算結果［5］，試驗結果是90年代在法國ONERA S2MA 1.77m×1.75m跨聲速風洞中完成的。2006年6月舉辦了第三次工作會議(DPW III)，此次會議提供了兩類共四種構型，一類是翼身組合體基本構型(DLR-F6)及修型構型(DLR-F6_FX2B)［6］，一類是機翼的基本構型(DPW_W1)及簡單優化構型(DPW_W2)。包含機翼構型的主要目的是鼓勵學術機構參與研討和開展網格收斂性的研究。本次會議的目的與上兩次相同，但更強調外形的局部修改對總體氣動特性的影響，組織形式也有所變化，最突出的不同在于沒有事前提供相應的試驗結果，只有不同軟件的計算結果可供比較。本文采用的試驗結果是2007年9月在NASA的國家跨音速設備(NTF)中完成的。

TRIP(TRIsonic Platform)是中國空氣動力研究與發展中心自行研發的CFD軟件，該軟件采用結構網格技術和有限體積方法，通過數值求解三維任意坐標系下的雷諾平均NS方程，數值模擬亞跨超飛行器的氣動特性和繞流流場。有關該軟件的基本功能介紹請參考文獻［7］。為進一步提高TRIP軟件的計算效率，適應千萬量級的網格規模的計算，滿足精細化流場數值模擬需求，課題組成員又進一步開發了TRIP軟件的并行版本，本文千萬量級的計算結果均采用了并行計算技術。

在2007年的工作中，針對DPW II提供的翼身組合體構型和翼/身/架/艙復雜組合體構型，我們詳細研究了網格密度、湍流模型對上述兩種構型的總體氣動特性影響，其中掛架和吊艙安裝阻力的計算精度與相應的實驗結果取得了較好的一致［8］。本文工作的主要目的是研究網格密度對運輸機構型計算結果的影響，重點是CFD軟件模擬局部修型后氣動特性的改變量。利用DPW III提供的多塊結構網格，本文詳細研究了網格密度對兩種機翼構型和兩種翼身組合體構型氣動特性的影響。本文采用波音公司的Edward N.Tinoco采用CFL3D軟件得到計算結果和NFT(National Transonic Facility)的試驗結果作對比分析。

1 機翼構型的計算網格和計算狀態

本文采用的計算網格來自DPW III，該結構網格由ICEM軟件生成，網格結構為多塊對接網格(1-to-1)，網格分為粗網格(Coarse)、中等網格(Medium)和細網格(Fine)和極細網格(Very Fine)四種，DPW_W1構型網格的詳細信息如表1所示，DPW_W2構型的網格序列與此相同，需要說明的是CFL3D軟件采用的網格序列與本文不同。DPW_W2是DPW_W1的簡單優化外形，二者的平面參數與厚度相同，對機翼的扭轉進行了優化。兩種典型運輸機機翼的計算構型和表面網格分布(中等)見圖1。

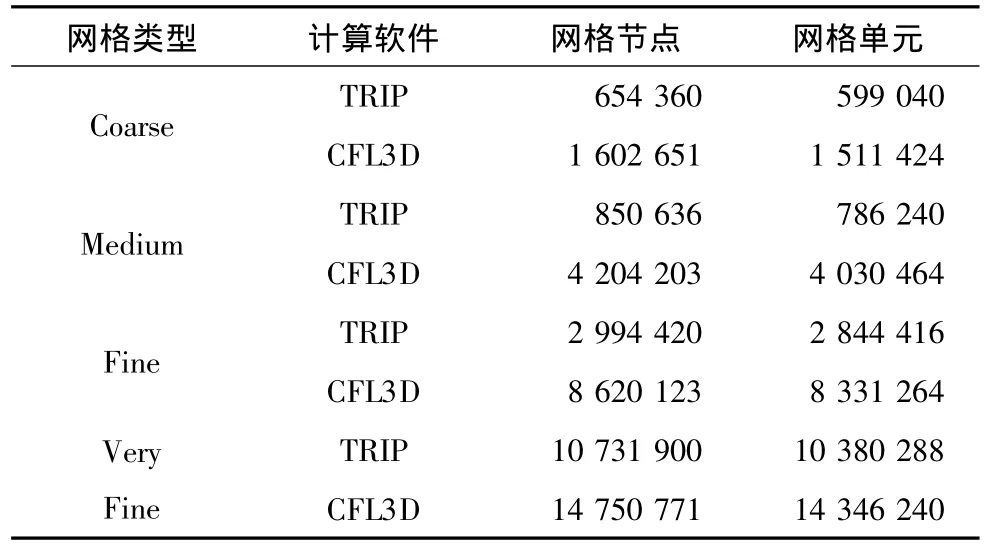
表1 標準網格統計列表(W1)Table1 GRID statistics for standard grids(W1)

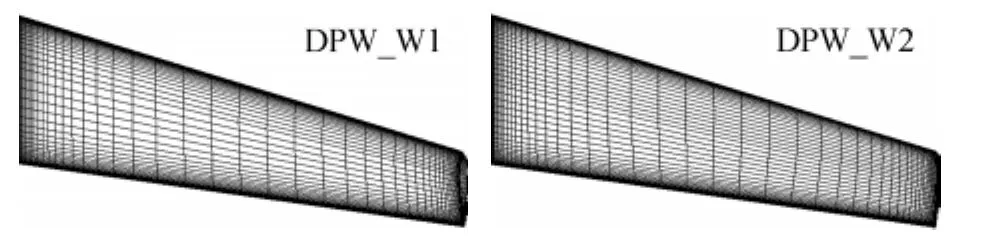
圖1 DPW機翼構型的表面網格(中等)Fig.1 Surface grids for wing configurations

本文的計算狀態如下:

算例1:網格收斂性研究

·M=0.76，Re=5.0×106(基于平均氣動弦長)

·α=0.5°

·全湍流計算

算例2:極曲線

·M=0.76，Re=5.0×106(基于平均氣動弦長)

·α =-1°，0°，0.5°，1°，1.5°，2°，2.5°，3°

·中等網格，全湍流計算

其中平均氣動弦長 C=0.1976m;參考面積 Sref=0.2903m2;壓心位置，ΔX=0.154245m，ΔZ=0.00m(距翼根頂點)。

1.1 算例1計算結果與分析

本文采用TRIP軟件，選擇二階精度的通量差分(FDS)類型的MUSCL差分格式和Menter的 SST兩方程湍流模型［9］模擬了上述兩種工況的流場，采用三重網格和并行技術加速收斂。對比計算結果采用了Tinoco采用CFL3D軟件得到的結果(見DPW網站)。必須說明的是CFL3D采用的網格序列與本文并不相同(見表1)，CFL3D采用的網格要比本文采用的網格規模大，這會對計算結果產生一定的影響。

1.1.1 網格收斂性研究

圖2給出了DPW_W1、DPW_W2兩種機翼構型采用粗網格、中等網格、密網格和極密四套網格得到的網格收斂性研究結果，同時還給出了采用CFL3D的計算結果，氣動橫坐標為網格節點的(-2/3)次冪，縱坐標為阻力系數。由圖2中可以看出，對于兩種機翼構型，本文采用SST兩方程模型均得到了網格收斂性結果。圖3給出了DPW_W2構型壓差阻力(CD_PR)和摩擦阻力(CD_SF)分量的網格收斂結果，可以看出隨著網格規模的增加，壓差阻力變化很大，而摩擦阻力變化較小，本文的計算結果與CFL3D相比較，同等網格規模下壓差阻力很接近，本文的摩擦阻力略小一些。DPW_W1的結果與此類似。考慮到本文采用的網格序列與CFL3D采用的網格序列不同，本文算例2計算結果主要采用密網格(2，844，416)的計算結果與CFL3D采用中等網格(4，030，464)的計算結果相比較。

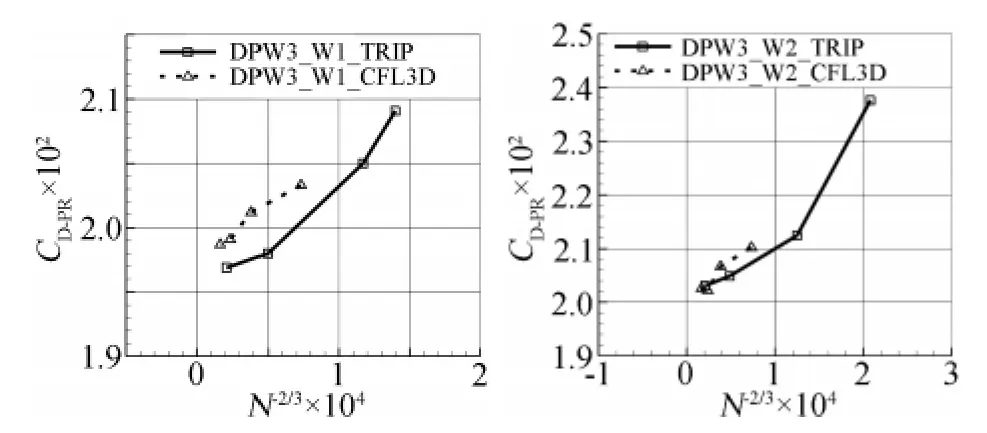
圖2 DPWIII機翼構型的網格收斂性研究Fig.2 Grid convergence of DPW_W1/W2

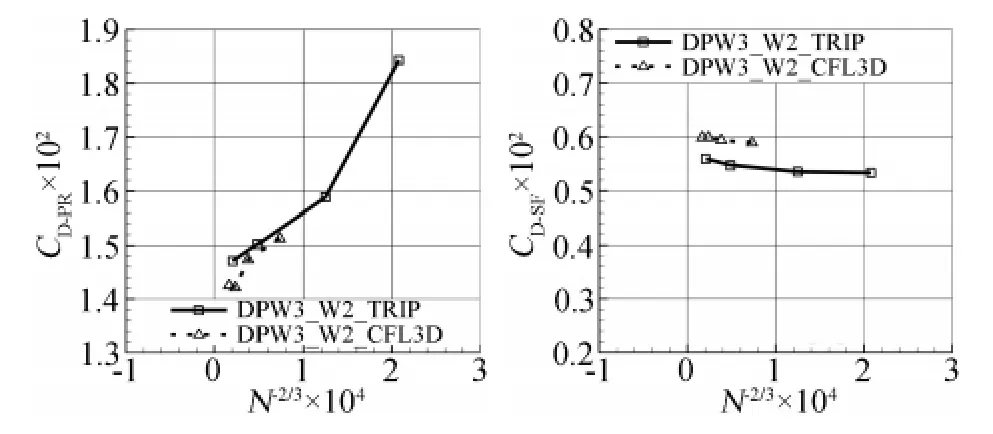
圖3 DPW_W2阻力收斂性研究Fig.3 Grid convergence of drag fraction for DPW_W2

1.1.2 壓力分布的比較

圖4、圖5給出了DPW_W1和DPW_W2兩種構型在55.1%、81.4%兩個典型站位上的壓力分布，其中的實線是CFL3D采用1435萬網格得到的結果，點劃線是TRIP軟件采用284萬網格得到的結果。由圖中可以看出，本文采用百萬量級網格得到的壓力分布與CFL3D采用千萬量級網格得到結果非常一致。顯示壓力分布對網格密度反映不敏感，或者說對于壓力分布的計算，本文采用的密網格已經足夠了。進一步比較圖4和圖5可以看到，在機翼中部和靠近翼梢站位上DPW_W2構型上表面的激波明顯弱于DPW_W1構型，但比較0.5°攻角的氣動特性比較可以看出(圖2)，激波的減弱并沒有使得該來流狀態下總的阻力的減少，反而使得總阻力略有增加，根本原因在于壓差阻力的略有增加，而摩阻變化不大。

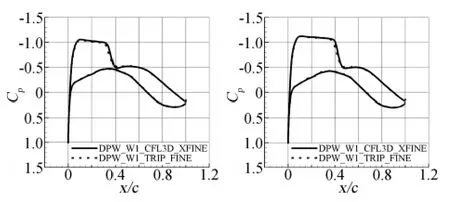
圖4 壓力分布的比較(DPW_W1)Fig.4 Comparison of Cp distribution(DPW_W1)

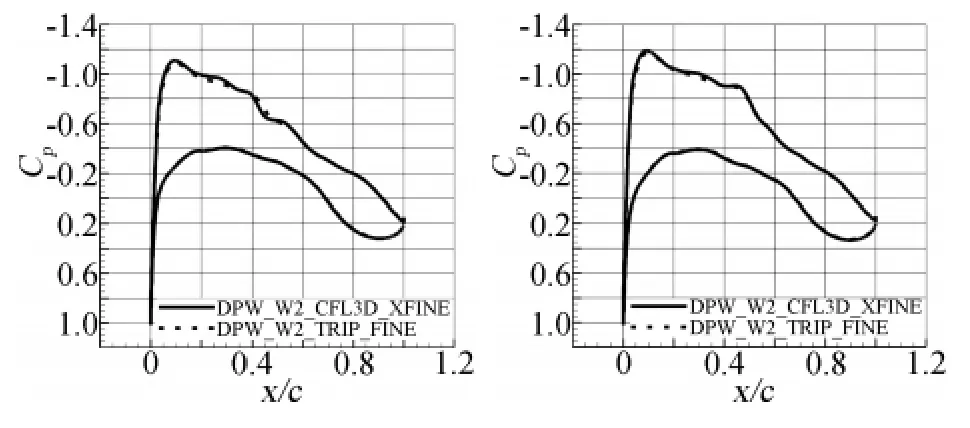
圖5 壓力系數的比較(DPW_W2)Fig.5 Comparison of Cp distribution(DPW_W2)

1.2 算例2計算結果及分析

圖6給出了DPW_W1/W2兩種機翼構型的極曲線和俯仰力矩系數曲線，其中極曲線的橫坐標采用了CD-Λ，其中Λ為展弦比，即總阻力減去誘導阻力，標識為CDP。TRIP軟件采用的是284萬網格點，CFL3D軟件采用的是403萬網格點，湍流模型均為SST兩方程模型。從極曲線可以看出，CFL3D的結果在升力系數0.46以下，TRIP的結果在0.45以下，DPW_W2的阻力系數大于DPW_W1的阻力系數;CFL3D的結果在升力系數0.46～0.66之間，TRIP的結果在在升力系數0.45～0.66之間，DPW_W2的阻力系數小于DPW_W1的阻力系數;升力系數大于0.66以后，兩種構型的阻力系數大致相當，采用兩種軟件得到的計算結果變化趨勢與兩種構型的阻力差量非常接近;兩種軟件得到的力矩特性有較大的差異，網格拓撲結構和計算方法細節處理的不同是導致差異的主要原因，但均反映出了以某一升力系數為分界線(TRIP軟件在0.58，CFL3D軟件在0.54)，兩種機翼構型的俯仰力矩系數變化出現交叉。

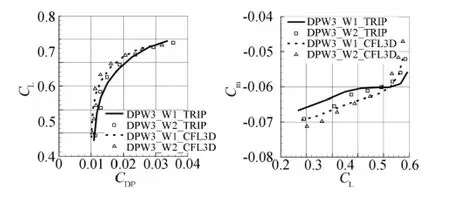
圖6 DPW-W1/W2構型氣動特性比較Fig.6 Aerodynamic coefficients of DPW-W1/W2 configuration

2 翼身組合體構型的計算網格和計算狀態

DPWIII提供了兩種翼身組合體構型，一種是DLRF6構型，另一種是在DLR-F6_FX2B構型。其中DLRF6_FX2B構型是在F6構型的基礎上，通過增加翼身接合部的整流部件得到的，目的是減少DLR-F6構型翼身接合部的分離區。DPW的網站上提供了兩類多塊對接網格，一類是由波音公司的ZEUS系統先進處理軟件生成，另一類是由ANSYS公司的ICEM軟件生成。為了與波音公司CFL3D軟件的計算結果對比，我們采用了波音公司的多塊對接結構網格(1-to-1)，網格分為粗網格(Coarse)、中等網格(Medium)和細網格(Fine)三種，DLR-F6構型網格的詳細信息如表2所示，DLR-F6_FX2B構型的網格序列與此相同。圖7給出了兩種典型現代運輸機翼身組合體的計算局部構型和表面網格分布的局部放大圖。本文的計算狀態如下:

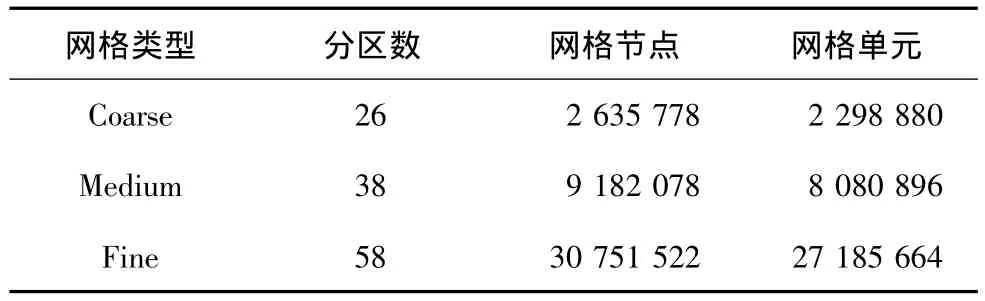
表2 標準網格統計列表(DLR-F6)Table2 Grid statistics for standard grids(WB)

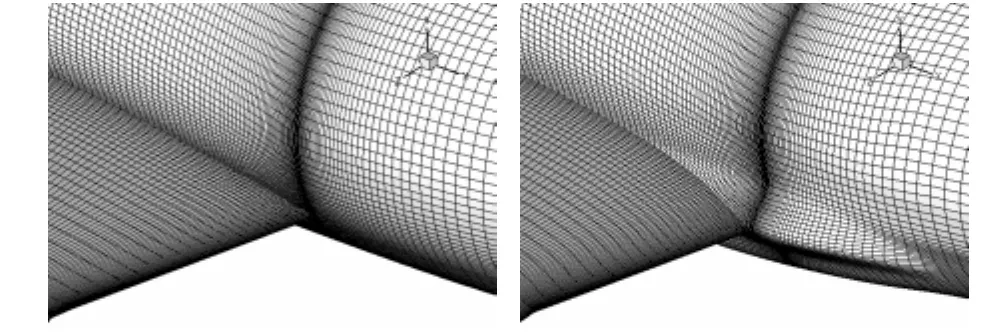
圖7 兩種翼身組合體構型的局部放大圖Fig.7 Surface grids for wing-body configurations

算例1:網格收斂性研究

·M=0.75，Re=5.0×106(基于平均氣動弦長)

·CL=0.500(±0.001)

·全湍流計算

算例2:極曲線

·M=0.75，Re=5.0×106(基于平均氣動弦長)

·α =-3°，-2°，-1°，-0.5°，0°，0.5°，1°，1.5°

·中等網格，全湍流計算

其中平均氣動弦長C=0.1412m;參考面積Sref=0.1453m2;壓心位置，ΔX=0.5049 m，ΔZ=-0.05142m(據機頭頂點)。需要注意的是，DPWII相同構型的雷諾數為300萬，而DPWIII的雷諾數為500萬。

2.1 算例1計算結果與分析

圖8給出了DPW-F6、DPW-F6_FX2B兩種翼身組合體構型采用粗、中和密三套網格得到的阻力系數、摩擦阻力系數的網格收斂性計算結果，同時還給出了采用CFL3D的計算結果。需要說明的是，CFL3D除了給出了如表2所示的三種網格的計算結果外，還給出了網格規模為1586萬網格點數的計算結果。可以看到本文采用TRIP軟件得到了網格收斂的計算結果。在升力系數0.5條件下，DPW-F6_FX2B的阻力系數略小于DPW-F6的計算結果，隨著網格密度的增加，兩種構型的阻力差量有變小的趨勢。以F6構型中等網格的計算結果為例，TRIP軟件得到的壓差阻力比CFL3D大2個阻力單位，而摩擦阻力則小12個阻力單位，總體來說，TRIP軟件的阻力計算結果比CFL3D小10個阻力單位左右。以F6構型為例，隨著網格密度的增加，TRIP軟件的阻力變化量在7個阻力單位左右，其中壓差阻力變化量在10個阻力單位，摩擦阻力的變化量在3個阻力單位左右，這再一次說明了網格密度的變化主要影響壓差阻力，而摩擦阻力對網格密度的變化不是很敏感。

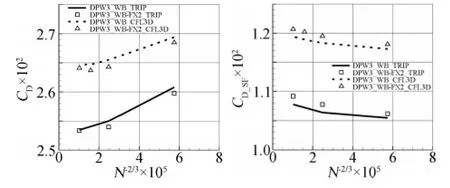
圖8 翼身組合體構型的網格收斂性曲線Fig.8 Grid convergence of wing-body configuration

在2008年的參考文獻［10］中給出了NTF的試驗結果。本文采用Richardson外推的方法，由中等網格與密網格的計算結果得到網格無關的氣動特性。固定升力系數下，DLR-F6及其修型構型的Richardson外推值及相應的試驗結果如表3所示。對于DLR-F6構型，試驗得到的阻力系數為0.02752±0.00014，理想阻力系數為0.01915±0.00014，與相應的試驗結果相比較，計算得到的阻力系數和理想阻力系數均小23個阻力單位;對于DLR-F6-FX2B構型，試驗得到的阻力系數為0.02728±0.00019，理想阻力系數為 0.01851±0.00019，與相應的試驗結果相比較，計算的阻力系數和理想阻力系數均小20個阻力單位。修型前后試驗阻力差量為-0.00024±0.00033，計算得到的修型前后的阻力差量為0.00006，在試驗精度范圍之內。

圖9 翼身組合體構型翼身接合部的表面流線Fig.9 Surface streamline of wing-body configuration

圖9給出了 DPW-F6(左)、DPW-F6_FX2B(右)兩種翼身組合體構型采用中等網格得到的翼身接合部的表面流線圖。對DPW-F6修型的主要目的就是減少翼身接合部的分離區，可以看到本文的計算結果準確反映了修型前后翼身接合部分離區的變化。

2.2 算例2計算結果與分析

圖10給出了TRIP軟件和NFT試驗給出的兩種翼身組合體構型的縱向氣動特性，其中極曲線的橫坐標為CDP。可以看到，相同攻角下，計算得到的升力系數偏高，但計算與試驗均反映出修型后相同攻角下的升力系數略有減少;相同升力系數下，計算得到的阻力值偏小，但計算與試驗均反映出升力系數0.5以下，修型后阻力系數略有降低且計算與試驗二者差量接近，升力系數大于0.5后，修型前后的阻力差量變小;相同升力系數下，計算得到的低頭力矩偏大，但計算與試驗均反映出修型后低頭力矩增加且計算與試驗二者差量基本一致。

圖10 翼身組合體構型氣動特性曲線Fig.10 Aerodynamic coefficients of wing-body configuration

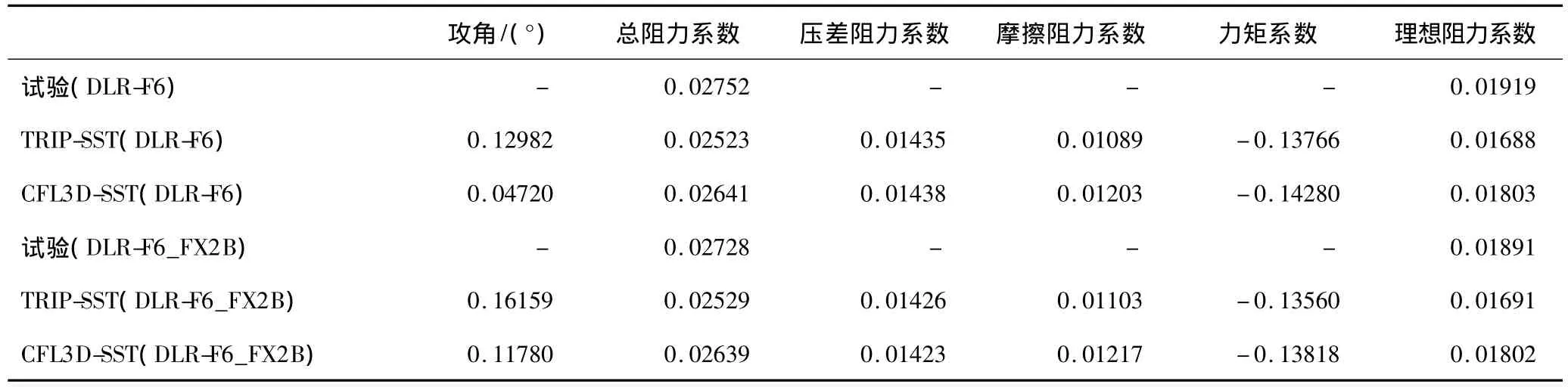
表3 DLR-F6/FX2B構型計算結果外推值(M=0.75，C L=0.50)Table3 Case1 DLR-F6/FX2B data extrapolated to continuum(M=0.75，C L=0.50)

3 結論

采用TRIP軟件，利用DPW III提供的多塊對接網格數值模擬了DPW_W1/W2兩種機翼構型和DLR-F6/F6_FX2B兩種翼身組合體構型，本文主要研究了網格密度對總體氣動特性和典型站位壓力分布的影響，通過與CFL3D的計算結果和NTF相應的試驗結果對比，得到以下一些基本結論:

(1)采用SST湍流模型，本文得到了網格收斂性的結果;網格密度的變化主要影響壓差阻力，對摩擦阻力的影響較小。

(2)攻角α=0.5°時，DPW_W2構型機翼上表面的激波強度明顯弱于DPW_W1構型;升力系數CL=0.5條件下，DPW-F6翼身組合體修修型后，翼身接合部的分離區明顯減弱。

(3)對于機翼構型和翼身組合體構型，本文的計算結果反映了修型前后氣動特性的變化量。相同升力系數下，本文計算得到的翼身組合體修型前后的升力系數、阻力系數和俯仰力矩系數變化量與試驗結果相當。

［1］TINOCO E N，BOGUE D R.Progress toward CFD for full flight envelope［J］.Aeronautical Jounal，2005，109(1100):451-460.

［2］JOHNSON F T，TINOCO E N，JONG Y.Thirty years of development and application of CFD at Boeing commercial airplane SEATTLE［R］.AIAA 2003-3439.

［3］OBERKAMPF W L，TRUCANO T G.Verification and validation in computational fluid dynamics［J］.Progress in Aerospace Sciences，2002，38:209-272.

［4］LEVY D W，ZICKUHR T，VASSBERG J，et al.Summary of data from the first AIAA CFD drag prediction workshop［R］.AIAA 2002-0841.

［5］LAFLIN K R，KLAUSMEYER S M，ZICKUHR T.Summary of data from the second AIAA CFD drag prediction workshop［R］.AIAA 2004-0555.

［6］VASSBERG J C，SCLAFANIA J，MARK A D.A wing-body fairing design for the DLR-F6 model:a DPW-III case study［R］.AIAA 2005-4730.

［7］王運濤，王光學，洪俊武，等.TRIP 2.0_SOLVER的開發與應用［J］.空氣動力學報，2007，25(2):163-168.(WANG Y T，WANG G X，HONG J W，et al.Development and application of TRIP 2.0_SOLVER［J］.ACTA Aerodynamica Sinica，2007，25(2):163-168.in Chinese)

［8］王運濤，王光學，張玉倫.TRIP 2.0軟件的確認:DPW II復雜組合體的數值模擬［J］.航空學報，2008，29(1):34-40.(WANG Y T，WANG G X，ZHANG Y L.Validation of TRIP 2.0:numerical simulation of DPW II complex con figuration［J］.ACTA Aeronautica et Astronaautica SINICA，2008，29(1):34-40.)

［9］MENTER F R.Improved two-equation k-ω turbulence models for aerodynamic-flows［R］.NASA TM-103975，1992.

［10］VASSBERG J C，TINOCO E N，MANIM.Comparison of NTF exprrimental data with CFD predictions from the third AIAA CFD drag prediction workshop［R］.AIAA 2008-6918.