基于守恒型嵌合體技術的多段翼型縫道參數分段進化優化設計研究

徐康樂，孫 剛

(復旦大學，上海 200433)

0 引言

增升裝置大迎角氣動特性的優劣決定了大展弦比飛機的低速氣動特性的好壞，二維多段翼型設計是三維增升裝置設計的基礎，其中多段翼型縫道參數對增升裝置的性能有重要影響，有必要開展多段翼型縫道參數分段進化優化設計研究。

目前對多段翼型復雜流場的數值模擬已較為成熟，對于大迎角有分離流動的多段翼型還有待于進一步的精確模擬，繞多段翼型高質量貼體結構化網格有助于大迎角有分離流動的精確模擬，使用嵌套網格技術可簡化多段翼型復雜外形貼體網格生成，文獻［1］表明對于存在有強梯度解以及強流動分離的復雜流場，傳統嵌合體技術各子域流場信息交互所采用的直接插值方法往往不具有物理守恒特性，從而影響數值解的精度，守恒型的流場信息傳遞方式可提高數值模擬的精度。

遺傳算法結合CFD技術在飛機優化設計中已有廣泛的應用。究其原因在于，遺傳算法具有魯棒性好、優化參數多且優化結果具有全局最優等特點。文獻［2，3］基于遺傳算法，提出一種新的翼型幾何定義方式，對跨音速翼型進行了優化設計。文獻［4］基于多個相互沖突設計原則，通過合理搭配編碼方式、交叉算子和變異算子解決了端點效應，設計了Pareto基因遺傳算法，然后將此算法應用于多目標的機翼優化設計中獲得了令人滿意的結果。Boris Epstein，Sergey Peigin［5］對 ARA M-100 機翼-機身構型及其上的升力面進行了多目標多約束的遺傳優化設計。國內學者王曉鵬［6］、隋洪濤［7］在氣動外形遺傳優化設計上進行了許多有效的嘗試。

本文對傳統嵌合體技術進行改進，采用具有質量通量全局守恒特性的流場信息交互方式，使其發展成為守恒型嵌合體技術。結果表明，在大迎角條件下，采用守恒型嵌合體技術所獲得的數值解，相較于非守恒格式具有更高的精度和更好的收斂性能。此外在標準遺傳算法的基礎上，為提高遺傳效率，加速進化過程，采用分段進化策略耦合Navier-Stokes方程求解器，以大迎角狀態下的升力系數為優化目標，對多段翼型的縫道參數(δs，0/L，Gap，δf)進行了遺傳優化設計。設計結果表明最終獲得的多段翼型構型的最大升力系數相較于初始構型具有顯著的提高，同時具有良好的失速特性，升力曲線以及極曲線。

1 基于質量通量守恒的插值方式

實現內外邊界的全場通量守恒性插值是一個具有挑戰性的但對嵌套網格技術而言是至關重要的問題。在此方面，早期的具有代表性的研究學者有Benek［8］、Rai［1］、Berger［9］等。多塊網格間干擾信息的有效傳遞問題迄今仍未能獲得徹底滿意的解決，其原因在于很難獲得同時實現多個通量，如質量通量、動量通量及能量通量的全局守恒形式。因此在運用多塊網格技術研究粘性流動初期，研究學者往往只考慮質量通量的全局守恒。學者 Tang H S［10，11］及 Jones S C［10］在標準的線性插值的基礎上，考慮內外界面處質量通量的守恒性質提出一種基于質量通量守恒的插值算法(MFBI)。該算法形式簡單，與標準的線性插值算法相比，考慮了流動的物理性質因此具有明顯的物理意義，而且具有與直接插值相同的數值精度，具有廣闊的工程應用前景。

MFBI算法是依據界面處質量通量守恒方程式推出各個速度分量當滿足質量通量守恒時所需滿足的關系，而所傳遞的擾動壓力值則直接是線性插值后所得的結果，因此該算法保證了質量通量的全場守恒而不能保證動量通量的全場守恒。

考慮圖1中兩個重疊區域ΩA及ΩB，ΓA、ΓB分別是區域ΩA、ΩB非重疊部分的區域邊界，Γa、Γb是重疊部分的區域邊界，n為邊界法向，F為質量通量。

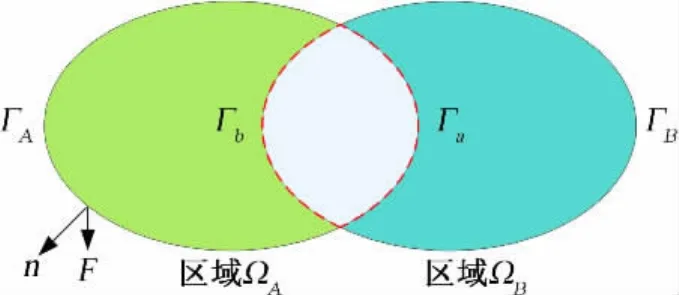
圖1 重疊區域Fig.1 Overlapped areas

圖2 重疊區域離散網格Fig.2 Overlapped grids

由通量守恒關系可以得到:

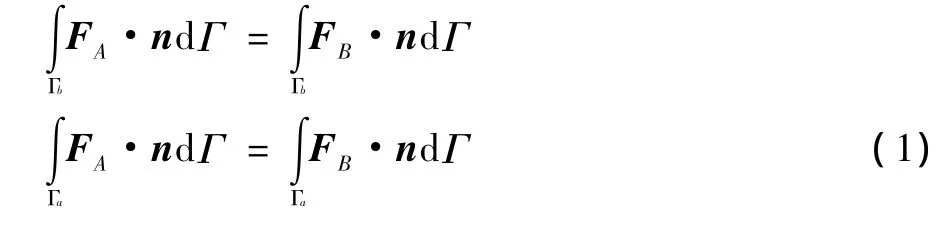
兩重疊區域的離散網格如圖2所示，我們選取圖中曲線Γ'為重疊區域的邊界，將式(1)在上述邊界上進行離散化，而邊界處的速度值由上、下一層網格點上的速度值插值得到。

式(1)離散后:

上式中p和q分別代表上、下一層網格點，U、F分別為速度和質量通量沿著曲線坐標系的第一個分量。

將區域B處的流場信息通過重疊區域傳遞到區域A，可得:

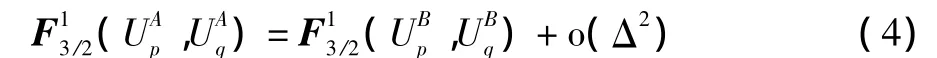
式(4)稱為MFBI算法的一般形式。將方程(4)在Γ'處泰勒展開后得到:

將式(7)應用于式兩側便可得到:

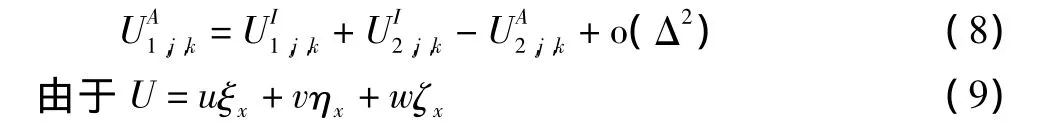
式中u、v、w為速度矢量的笛卡爾分量。由泰勒展開，為保證上式成立，需滿足下式:

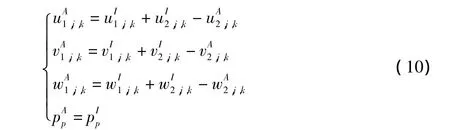
式(10)便是完整的MFBI算法形式。

本文對遺傳優化的初始構型在15°迎角，Re數為455萬以及Ma數為0.17的流動狀態下進行了數值模擬并將其與非守恒結果進行了對比分析。圖3給出了計算過程中嵌套網格在主翼前后緣挖洞后的效果。圖4給出了重疊邊界面上質量通量以及速度通量的歷史曲線，從圖中可以看出，采用守恒型嵌套方式時，在閉合重疊界面上的質量通量為零，而速度通量明顯低于非守恒格式。此外，文獻［12-13］研究表明，在多段翼型復雜繞流數值模擬中，采用守恒型的信息傳遞方式所獲得的數值解較之非守恒形式具有更好的數值精度，與試驗結果也更加符合。

圖3 嵌套網格在主翼前后緣挖洞后效果Fig.3 Details of effects after hole cutting

圖4 重疊邊界面上質量通量以及速度通量的歷史曲線Fig.4 History of mass and velocity flux through closed overlapped area

2 縫道參數的優化

由于遺傳算法具有高魯棒性以及全局最優性等優點，使得其在飛機優化設計中有廣泛的應用。標準的遺傳算法通常包括:選擇、交叉、變異等操作。二進制編碼方式在交叉，變異遺傳操作中容易實現，因此在對染色體進行編碼時通常采用二進制方式。然而在遺傳優化設計過程中，表征飛行器部件幾何特征的參數往往有很多個，如對三段式多段翼型縫道參數進行遺傳優化時將包括縫翼及襟翼的偏轉角、搭接量以及縫道寬度，也即δs，O/Ls，Gaps，O/Lf，Gapf，δf，其定義如圖 5 所示。當將這些幾何參數全部同時作為優化參數進行遺傳編碼時，使得最后所表征種群個體的染色體長度過長，此外在求解高維函數優化問題或當求解精度要求較高時，二進制編碼的位串過長，會使得算法的搜索效率大大降低。

圖5 多段翼型縫道參數Fig.5 Configure parameters of multi-element airfoils

本文應用如下分段進化策略加以解決。

所謂分段進化，即若按所要求精度應為每個分量分配(m+k)個二進制位，則首先為每個子串分配m個二進制位，而后經進化得一最優化位串(n×m位)并將其保留，而后為每個位串分配(k+1)個二進制位，繼續進行優化。但進行適應度計算時，則需將x*的相應子串的前(m-1)位連于后產生的(k+1)位之前，再按(m+k)位進行計算。最后將如此得到的最優個體n×(k+1)位連于第一階段產生出的由n個m位子串所組成的最優個體x*的相應(m-1)位子串之后(覆蓋原m位子串的第m位)，形成每個子串為(m+k)位長的最優個體。可以證明，如此產生的最優個體其分量的精度滿足原(m+k)位的精度要求。

事實上，按前述表示方式，第i個(m+k)位子串經解碼再映射得到的表型為:

而由m位子串與k位子串合成得到的表型為:

由式(11)和式(12)可得:

在求解高維函數優化問題或當精度要求較高而必須使用較長的二進制位串時，采用上述分段進化策略可有效避免因位串過長而影響搜索效率。

3 優化結果及分析

在此次優化設計過程中，以18°迎角、來流馬赫數Ma為0.2、雷諾數Re為5×106的工況條件下多段翼型的升力系數作為遺傳個體的評價函數，以N-S方程作為流場控制方程，采用守恒型的嵌合體技術對每個個體進行評價。優化變量的搜索空間如下表1所示，δs，O/L，Gap，δf。初始種群數目為5，進化代數為40且在20代后進行分段進化。

表1 縫道參數搜索區域Table1 The searching range of the configuration parameters

圖6給出了種群進化過程中當代最優個體適應值函數的優化過程;圖7給出了進化過程中初始種群，以及第10代、第38代、第39代和第40代種群中最優個體的多段翼型構型。從上圖可以看到，初始構型與最優構型相差較大，然而在接近收斂的狀態下，各代最優個體構型十分接近。對于前緣增升裝置而言，其各個縫道參數均有較大變化。對于后緣增升裝置，后緣縫道搭接量變化較少而后緣偏轉角變化量較大，由此也說明升力系數對后緣偏轉角更為敏感。

對于增升裝置而言，其最大升力系數是最為重要的設計指標之一。上述優化過程只是針對不同構型在18°迎角下的升力系數進行的，然而對于一副具有良好氣動性能的多段翼型構型而言，其臨界迎角往往大于18°，或者說18°迎角往往接近多段翼型構型的臨界迎角。此外，由于翼型在失速前升力曲線呈線性關系，因此可以選取其中一個狀態作為設計點，從而使得整條升力曲線往上平移，也即增大了多段翼型的零升迎角，同時也滿足提高最大升力系數CLmax的要求。因此，上述的優化過程具有合理性。從圖8可以看到，最大升力系數以及零升迎角均隨著遺傳進化而不斷得到提高，由此也可以說明此次的優化結果是理想的。圖9是最終構型在不同狀態下的流線圖。

圖6 遺傳進化過程Fig.6 Evolution history

此外，從圖6可以看出基于守恒型嵌合體技術所獲得的遺傳優化結果相較之非守恒結果具有明顯的差別，具體體現在:一方面，基于守恒型嵌合體技術的遺傳進化過程對每一代最優個體的適應值的評價不同于非守恒方法，并且我們認為守恒格式對每代自適應值的評價較之非守恒格式更為準確，原因在第2小節已經闡述;另一方面，由于采用守恒型嵌合體技術的流場求解器較于非守恒格式精度更高，使得在遺傳進化過程中當算法接近收斂時或者鄰近兩代最優個體的構型差異很小時，如圖6中所示的A、B兩個階段，算法仍然能夠分辨出個體間適應值的差異，從而避免遺傳算法提前收斂。

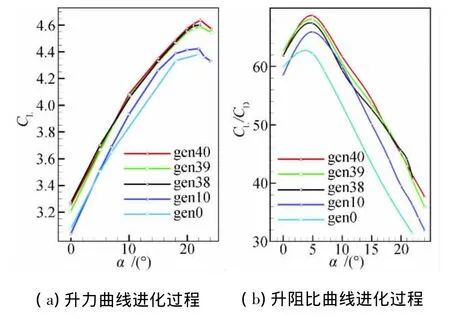
圖8 不同進化構型的升力曲線及升阻比曲線Fig.8 Lift and polar curves of different configurations during evolution

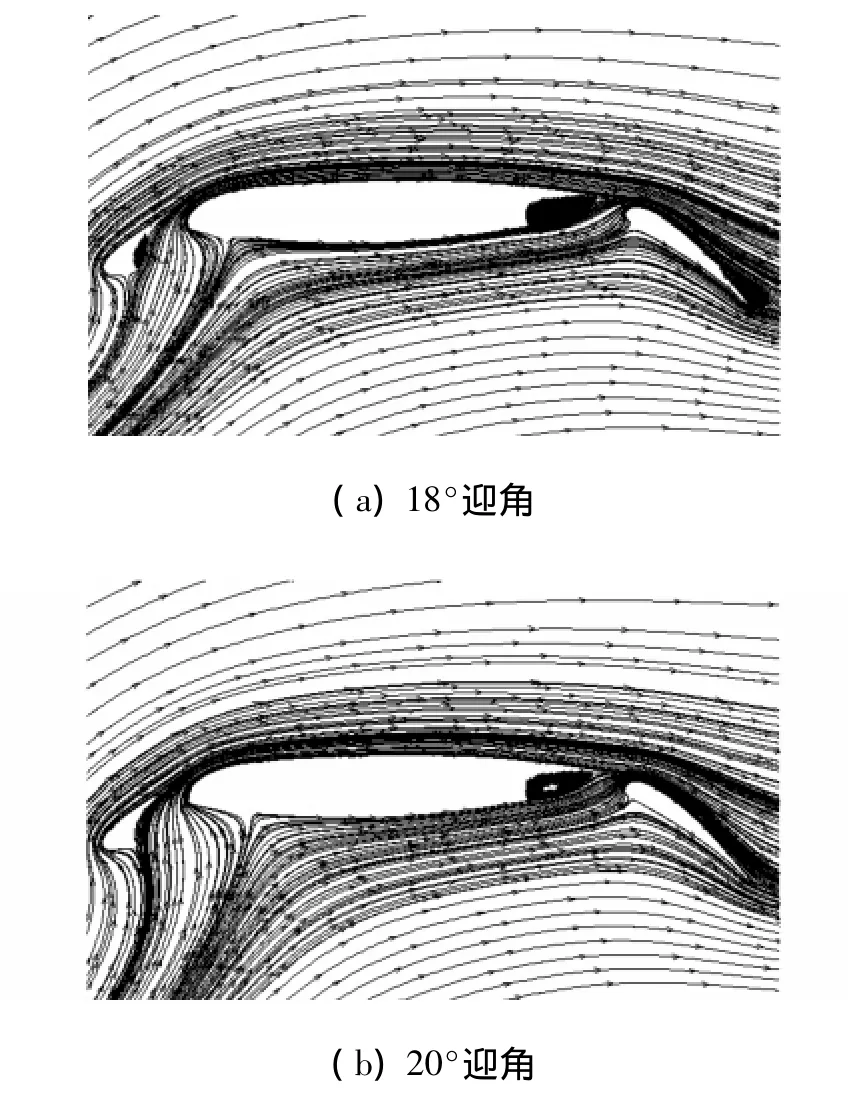
圖9 最終構型在不同狀態下的流線圖Fig.9 Stream traces of the optimal configure at different attack angles

4 結論

通過基于具有質量通量全局守恒特性的守恒型嵌合體技術，采用分段遺傳進化策略，以大迎角狀態下的升力系數為優化目標，對多段翼型的縫道參數(δs，O/L，Gap，δf)進行了遺傳優化設計:

(1)在大迎角條件下，采用守恒型嵌合體技術所獲得的數值解，相較于非守恒格式具有更高的精度以及更好的收斂性能。同時，守恒型算法在遺傳進化接近收斂狀態仍然能夠分辨出差異較小個體間適應值的差別，從而避免遺傳算法提前收斂。

(2)設計結果表明最終獲得的多段翼型構型的最大升力系數相較于初始構型具有顯著的提高，同時具有良好的失速特性，升力曲線以及極曲線。

(3)對于多段翼型構型，以18°迎角下的升力系數作為遺傳優化的評價函數，在獲得優化結果后，再綜合評價最后幾代遺傳種群中的最優個體。此種思路，在保證優化效率的同時，以實現對初始構型氣動性能的最優化。

［1］RAI M M.A implicitconservative zonal-boundary scheme for Euler equation calculations［R］.AIAA 85-0488，1985.

［2］ABDURRAHMAN H，IBRAHIM O.Transonic airfoil design and optimisation by using vibrational genetic algorithm［J］.Aircraft Engineering and Aerospace Technology，2003，75(4):350-357.

［3］AVA SHAHROKHI，ALIREZA JAHANGIRIAN.Airfoil shape parameterization for optimum Navier-Stokes design with genetic algorithm［J］.Aerospace Science and Technology，2007，(11):443-450.

［4］LEE D S，GONZALEZ L F，PERIAUX J，SRINIVAS K.Robust design optimisation using multi-objective evolutionary algorithms［J］.Computers ＆ Fluids，2008，37:565-583.

［5］BORIS E，SERGEY P.Accurate CFD driven optimization of lifting surfaces for wing-body configuration［J］.Computers ＆Fluids，2007，36:1399-1414.

［6］王曉鵬.遺傳算法極其在氣動優化設計中的應用［D］.西安:西北工業大學，2000.

［7］隋洪濤.基因遺傳算法及氣動外形最優化設計［D］.南京:南京航空那個航天大學，2001.

［8］BENEK J A，STERGER J J，DOUGHERTY F C.A flexible grid embedding technique with application to the Euler equations［R］.AIAA 83-1944-CP，1983.

［9］BERGER M J.On conservation at grid interfaces［J］.SIAM Journal on Numerical Analysis，1987，24(5):967-984.

［10］TANG H S，JONES S C，SOTIROPOULOS F.An overset grid method for 3D unsteady incompressible flows［J］.Journal of Computational Physics.2003，191:567-600.

［11］TANG H S.Numerical simulation of unsteady three dimensional incompressible flows in complex geometries［D］.Dissertation，Atlanta:School of Civil and Environmental Engi-neering，Georgia Institute of Technology，GA 30332-0355，2001.

［12］XU K L，SUN G.Assessmentofan interface conservative algorithm MFBI in a chimera grid flow solver for multi-element airfoils［A］.Proceedings of the World Congress on Engineering 2009 Vol II［C］.London:World Congress on Engineering 2009，2009:1702-1706

［13］XU K L，SUN G.On interface conservative attributions for computations of the complex flows of high-lift system based on chimera technique［A］.Proceedings of2010 The 2nd International Conference on Computer and Automation Engineering［C］.Singapore:ICCAE，2010:279-283.