辨識航行體水動力參數的智能方法

陳瑋琪，顏 開，王寶壽

（中國船舶科學研究中心，江蘇 無錫 214082）

1 引 言

水動力參數是設計水下航行體，如魚雷、水下機器人等的原始數據，流體動力計算、風洞和水池試驗是獲取這些數據的常用手段，但由于實航環境的復雜性，這些手段獲得的水動力參數與實航的水動力參數還是有較大的差別。因此應用辨識技術[1]從水下航行體的航行試驗數據中提取它的流體動力參數具有重大的實際意義。

蔡金獅在文獻[1]中總結了魚雷水動力參數辨識的極大似然法；丁文鏡利用極大似然法[2]和預報誤差法[3]研究了受控航行體水動參數的辨識；劉建成探討了極大似然法及其松弛算法在水下機器人水動參數的辨識中的應用[5]；傅慧萍比較了牛頓-拉夫遜算法、單純形法及模擬退火算法在水下運載器的水動力參數辨識中的優缺點[4]，研究表明，牛頓-拉夫遜算法、單純形法對初值要求較高，難以獲得全局優化解，而模擬退火算法則有相對較好的全局收斂性，模擬退火算法本身是智能優化算法的一種。陳瑋琪則將現代人工智能優化算法-群體智能優化算法PSO應用在水下航行體[6]的水動力參數辨識中,對物體出水過程[7-8]的水動力參數也進行過探索。這些研究表明，現代辨識技術通過引入最佳擬合準則將辨識問題轉化為確定性函數的優化問題后，采用現代智能優化算法[9-11]來辨識是一個發展趨勢。現代智能優化算法相對于經典的牛頓-拉夫遜算法具有很多優點，適合高維、多峰、連續性或可微性不好的非線性函數的全局優化，并且與函數的形式無關，因此，利用智能算法結合最小二乘準則就能獲得較好的結果。

本文將文獻[11]中發展出來的智能優化算法-微分群體算法（Different Swarm，簡稱DS）結合廣泛使用的最小二乘準則用于水下航行體縱向平面運動的水動力參數辨識，仿真辨識表明，結果要好于文獻[1]和文獻[3]中給出的經典結果，而且以往算法所無法辨識的附加質量也能同時辨識出來。

2 水下航行體的運動狀態方程

2.1 符號定義

ρ—水密度；

v—航行體運動速度；

L—航行體特征長度；

D—航行體直徑；

m—航行體質量；

Jx，Jy，Jz—航行體轉動慣量；

ωx，ωy，ωz—體坐標系下的角速度分量；

θ，ψ，γ—大地坐標系下的俯仰角、偏航角和滾動角；

vx，vy，vz—體坐標系下的速度；

x0，y0，z0—大地坐標系下的質心坐標。

2.2 平面彈道方程

在縱向運動中，令所有橫向運動參數 vz，ωx，ωy，ψ，φ，z0，β 為 0。 并假設浮心總在導彈的縱軸上，浮心位置 （xB，yB，zB）＝（xB，0，0 ），以航行體的重心為原點建立航行體體坐標系，則體坐標系下的縱向動力學方程：

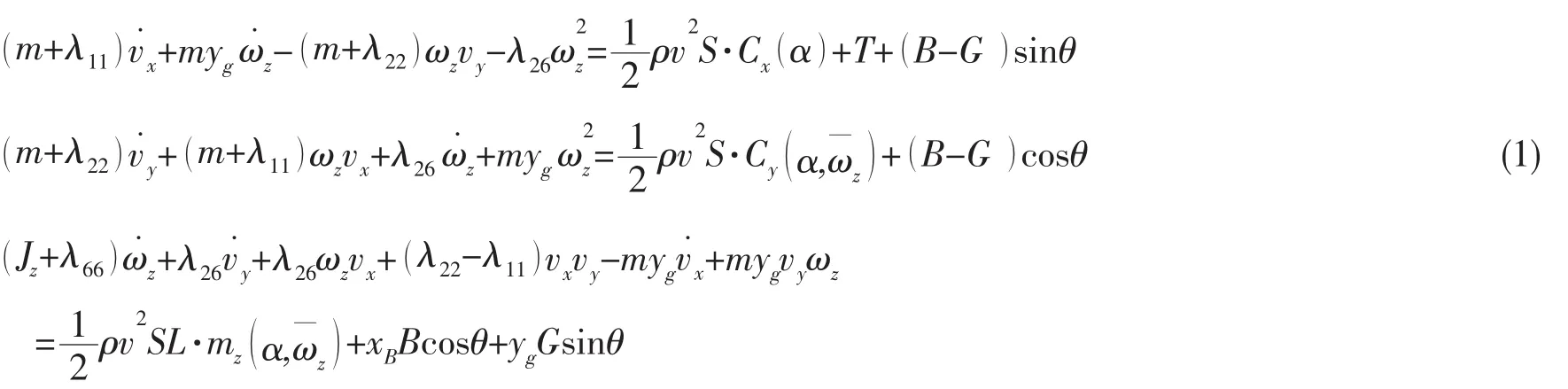
縱向運動學方程：

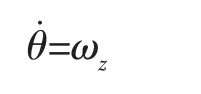
3 水動力模型

（1）式給出了與水動力相關的量。 根據流體力學理論，附加質量λ11，λ22，λ26，λ66在水下是常數，而與粘性作用力相關的水動力可以近似展開為水動力系數的一階線形模型：

待辨識的水動力參數共12個：

這里僅考慮全濕流狀態，忽略空泡的影響。

4 辨識原理和算法

辨識12個參數的算法是，從12個水動力參數的初始值出發，根據方程（1）計算航行體的彈道，然后比較計算彈道與試驗彈道之間的誤差，再根據誤差按一定方法逐步調整12個參數的值，最終使得計算彈道與試驗彈道之間的誤差達到最小，這時得到的12個參數值就是需要求解的水動力參數值。定義系統的狀態向量為

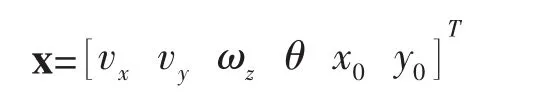
待辨識的未知水動力參數向量為

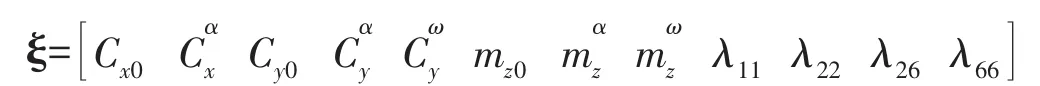
則方程（1）可以整理為標準形式

辨識準則采用最小二乘法，即求ξ，使得計算彈道xi與試驗彈道之間的誤差平方和達到最小

文獻[11]中所提出的DS智能優化算法[11]具有非常強大的約束優化能力，因此可以用于本問題。在DS中，每一個解稱為一個粒子，粒子在解空間中的位置就表示一個可能解，解的變化對應于粒子的飛行。初始時解空間中包含一個粒子群體，群體中每個粒子在解空間中飛行并相互交換信息，然后每個粒子根據獲得的信息確定下一步的飛行位置，直至找到最優解。DS中，粒子交換信息并改變位置的公式如下

這里，n表示粒子群體的個數，下標i表示的是第i個粒子，上標k表示第k步的飛行位置表示第i個粒子前k步所到達過的最好位置，表示整個粒子群在前k步所達到的最好位置，rk是[0 1]之間的隨機數，ω是算法參數，一般取為1，和表示粒子群中隨機選取的兩個粒子i1，i2的最好位置。經過一定的迭代步數就是J的最優解。

5 模擬辨識

為檢驗辨識算法的可行性，采用模擬彈道進行仿真辨識，方法如下，先選取已知的水動力參數，再根據方程（5），利用 Runge-Kutta（4，5）方法求解狀態方程（1），得到彈道運動狀態參數然后疊加上偽隨機數發生器產生的觀測噪聲ε，

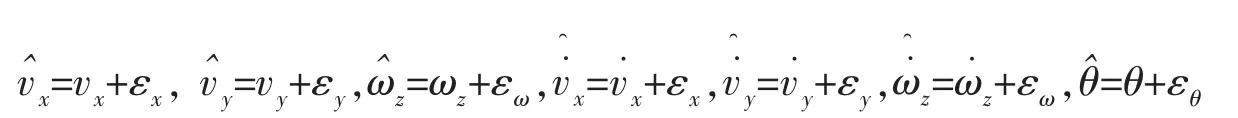
以模擬試驗觀測數據。最后根據模擬試驗觀測數據來辨識水動力參數，并和選取的已知水動力參數值進行比較。

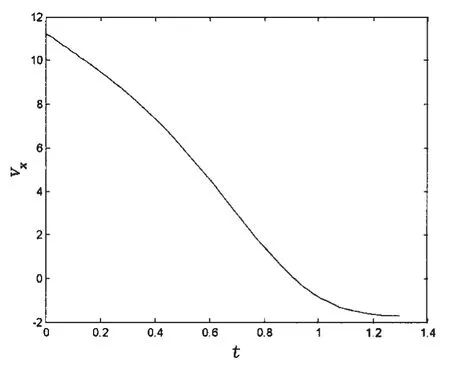
圖1 積分彈道曲線vxFig.1 The integral trajectory curve for vx

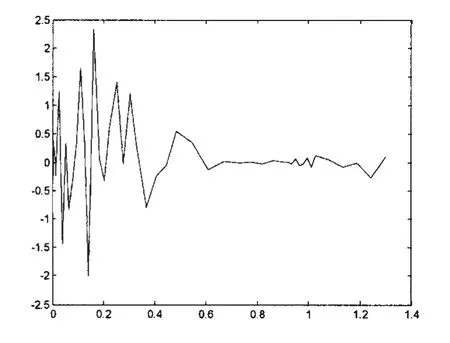
圖2 觀測噪聲Fig.2 The observed noise

模擬彈道的已知值見表1，初始值根據試驗數據的某一時間選取。圖1顯示了根據水動力參數已知值積分出來的模擬彈道曲線vx，圖2是偽隨機數發生器產生的觀測噪聲，圖3是彈道曲線vx疊加觀測噪聲得到的模擬觀測數據。

表1中列出了觀測噪聲水平分別為標準差0、1%、3%峰值下，辨識的水動力參數與已知精確值的比較（通常λ11非常小，這里不參與辨識）。

從模擬彈道的辨識結果來看，首先，算法在不同噪聲水平下，得到的辨識結果都和已知值吻合得相當好，最大相對誤差不超過7%，這說明了本文的算法是可行的，也是可靠的；從中還可以看出，觀測噪聲對結果的影響不大，這說明該算法具有很好的魯棒性；同時，該算法可以同時辨識出附加質量和其它水動力參數，而文獻[1]中基于極大似然法所提出的魚雷辨識算法則認為附加質量是不可以辨識的量，因此文中的算法更有優越性。另外，算法對初值幾乎沒有要求，可以從任意值開始進行搜索，而且速度極快，這是牛頓-拉夫遜算法所不具備的優勢。

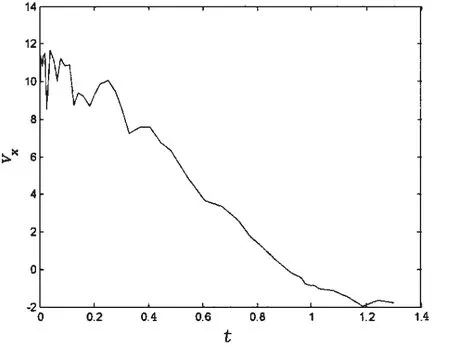
圖3 模擬觀測彈道Fig.3 The simulating trajectory

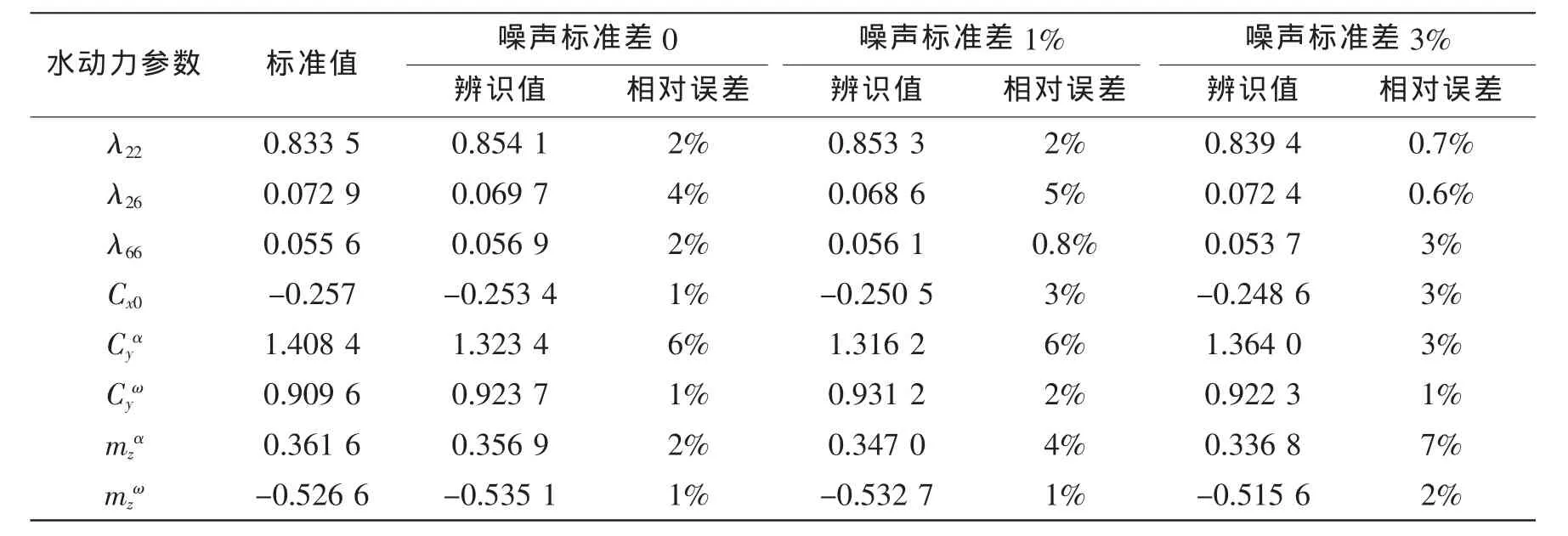
表1 仿真辨識結果比較Tab.1 Comparison between the identification simulating results

6 結 論

（1）和經典的牛頓—拉夫遜算法比較起來，智能辨識算法要簡單得多，因為智能算法過程無須考慮運動方程的復雜的數學形式，而且對初值要求不高，甚至幾乎沒有要求，這是經典辨識算法所不具備的優點，因此適合工程應用。

（2）此次研究雖然采用了平面彈道，但是由于辨識算法是通用的，因此換成6自由度全彈道方程來進行辨識是很容易做到的，而且算法對待辨識參數的維數不敏感。

（3）以后的工作將考慮空泡，并在水動力模型中增加空泡與水動力之間的模型，利用類似的辨識技術最終獲得帶空泡航行體的水動力參數及其模型。

[1]蔡金獅等.飛行器系統辨識學[M].北京:國防工業出版社,2003.

[2]丁文鏡,羅仁凡等.受控航行體水動參數的極大似然辨識[J].清華大學學報（自然科學版）,1992,2(32):89-95.

[3]丁文鏡,羅仁凡等.辨識航行器水動力參數的預報誤差法[C].魚雷控制系統學組學術交流會,1991.

[4]傅慧萍.潛射導彈運載器水彈道動力學系統建模理論與應用[D].西安:西北工業大學,2000.

[5]劉建成,劉學敏,徐玉如.極大似然法在水下機器人系統辨識中的應用[J].哈爾濱工程大學學報,2001,22(5):1-4.

[6]陳瑋琪,顏 開,史淦君,王士同,劉志勇.水下航行體水動力系數的智能辨識方法研究[J].船舶力學,2007,11(1):40-46.

[7]陳瑋琪,顏 開,史淦君,王士同.基于TSK智能技術的物體垂直出水水動力系數辨識研究[J].水動力學研究與進展,2005,20(4):445-451.

[8]陳瑋琪,顏 開.新的智能算法和物體斜出水水動力系數辨識[J].船舶力學,2008,12(2):204-210.

[9]Lu Haiyan,Chen Weiqi.Self-adaptive velocity particle swarm optimization for solving constrained optimization problems[J].Journal of Global Optimization,2008,41:427-445.

[10]Lu Haiyan,Chen Weiqi.Dynamic-objective particle swarm optimization for constrained optimization problems[J].J Comb.Optim.,2006,12(4):409-419.

[11]陳瑋琪.智能辨識技術及其在物體出水水動力參數辨識中的應用研究[D].無錫:江南大學,2008.