EPR核電站常規(guī)島主廠房風(fēng)洞試驗與風(fēng)致響應(yīng)研究
周向陽,張略秋,周雷靖,梁樞果,鄒 垚
(1.廣東省電力設(shè)計研究院 博士后科研工作站,廣州 510663;2.華南理工大學(xué) 土木與交通學(xué)院,廣州 510641;3.武漢大學(xué) 土木建筑工程學(xué)院,武漢 430072)
雖然核電是一種低碳能源,但在我國電力行業(yè)中所占比例不到2%,因此核電目前正處于快速發(fā)展的階段。EPR(European Pressurised Reactor)是歐洲第三代壓水堆型,具有很高的經(jīng)濟(jì)和技術(shù)性能。廣東臺山所引進(jìn)的EPR核電項目,是目前世界上唯一在建的第三代壓水堆型機(jī)組,一期工程共有兩臺機(jī)組,其單機(jī)裝機(jī)容量是目前我國已建和在建核電機(jī)組中單機(jī)容量最大的,達(dá)到了1 750 MW。由于核電工程特殊的安全要求,在廠址選址過程中,通過地質(zhì)勘查,避開了對核安全不利的地質(zhì)構(gòu)造。在這種情況下,風(fēng)荷載往往是核電站結(jié)構(gòu)的主要控制荷載,特別是沿海核電廠址中,不僅基本風(fēng)壓大,各類極端性氣候,如臺風(fēng)、龍卷風(fēng)等也有發(fā)生,結(jié)構(gòu)抗風(fēng)設(shè)計和評估尤其復(fù)雜,所以在第三代核電設(shè)計控制文檔中[1],強調(diào)了必須以風(fēng)洞試驗作為核電結(jié)構(gòu)風(fēng)荷載評估的技術(shù)手段。
由于臺山核電常規(guī)島主廠房跨度大,主廠房汽輪機(jī)和其它設(shè)備也較重,低階頻率較低,已為風(fēng)敏感結(jié)構(gòu)。而且現(xiàn)有的規(guī)范[2]也不能夠評估該結(jié)構(gòu)的風(fēng)振響應(yīng),因此本文以臺山EPR核電常規(guī)島主廠房為例,分析其動力特性,然后在考慮核島及其鄰近建筑物干擾的情況下,通過主廠房剛性模型測壓風(fēng)洞試驗,量測主廠房表面風(fēng)壓時程,得到主廠房的體型系數(shù)和極值風(fēng)壓。然后在頻域內(nèi)對脈動風(fēng)荷載所引起的主廠房位移風(fēng)振響應(yīng)和內(nèi)力風(fēng)振響應(yīng)進(jìn)行計算和分析。最后根據(jù)最優(yōu)化理論,給出了主廠房結(jié)構(gòu)的等效靜力風(fēng)荷載和風(fēng)振系數(shù)計算方法。研究的結(jié)論和方法可以為EPR三代核電主廠房抗風(fēng)設(shè)計和評估提供科學(xué)依據(jù)。
1 常規(guī)島主廠房的動力特性
1.1 頻率與振型
首先建立常規(guī)島主廠房有限元模型,主廠房豎向承重結(jié)構(gòu)和屋蓋均為鋼結(jié)構(gòu),內(nèi)部汽輪機(jī)平臺為鋼筋混凝土結(jié)構(gòu)。主廠房高度為52 m,寬度58 m,長度110 m;汽輪機(jī)平臺高度為21 m,寬度為22 m,長度為71 m,汽機(jī)平臺柱設(shè)置牛腿作為支座,通過鋼梁,與主廠房進(jìn)行連接;屋蓋為雙坡屋面,坡度5%。采用平面鋼桁架結(jié)構(gòu),跨度58 m,結(jié)構(gòu)整體有限元模型見圖1。

圖1 常規(guī)島主廠房有限元模型Fig.1 Finite element model of main powerhouse
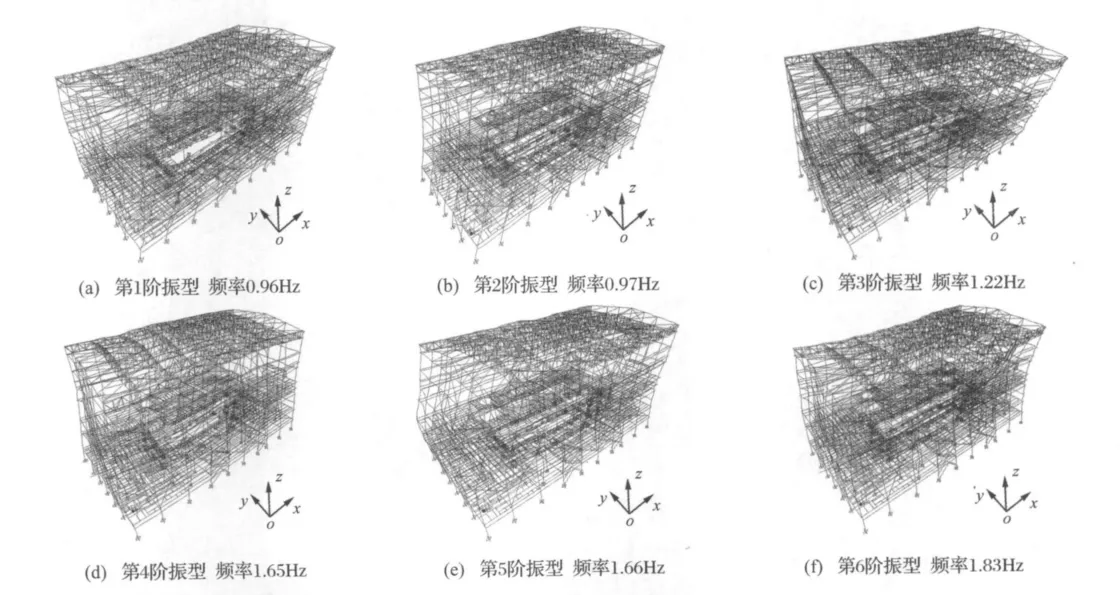
圖2 常規(guī)島主廠房前6階振型Fig.2 The first six mode of main powerhouse
根據(jù)有限元模型,進(jìn)行動力特性計算得到了結(jié)構(gòu)前25階頻率與振型,前6階的頻率與振型見圖2。可以看出,前3階振型形狀分別表現(xiàn)為整體結(jié)構(gòu)沿Y軸的彎曲振動,沿X軸振動以及繞Z軸的扭轉(zhuǎn)振動。第4階振型形狀為結(jié)構(gòu)沿X軸、Y軸的二階彎曲振動;由于主廠房樓板剛度的作用,第5階與第6階振型分別為25 m標(biāo)高以上的主廠房結(jié)構(gòu)沿X軸、沿Y軸的一階彎曲振動。限于篇幅沒有列出更高階振型的形狀與頻率,但是結(jié)構(gòu)的頻率分布比較密集,前25階頻率不超過4 Hz。
為了增加結(jié)構(gòu)的冗余度,屋蓋鋼桁架與柱采用剛性連接。因此,在某些振型中,不僅沿X軸向與沿Y軸向的振型是耦合的,而且豎向承重結(jié)構(gòu)與屋蓋結(jié)構(gòu)的振型也是耦合的,這可從圖3中主廠房第4階振型在XZ平面與YZ平面的投影看出。

圖3 主廠房縱向和橫向振型Fig.3 Plain mode of main powerhouse
1.2 各階振型阻尼比
由于常規(guī)島主廠房承重結(jié)構(gòu)為鋼結(jié)構(gòu),內(nèi)部汽輪機(jī)平臺是鋼筋混凝土結(jié)構(gòu),汽機(jī)平臺柱挑出牛腿作為支座,通過其上鋼梁與主廠房承重結(jié)構(gòu)連接。而這兩種結(jié)構(gòu)的阻尼有著很大的不同,作為整體結(jié)構(gòu),共同工作時需要考慮兩種材料所組成的結(jié)構(gòu)等效阻尼。根據(jù)建筑結(jié)構(gòu)荷載規(guī)范[2],對于鋼結(jié)構(gòu),各階振型阻尼比可取值為0.01,對于混凝土結(jié)構(gòu),各階振型阻尼比可取值為0.05。在復(fù)阻尼理論[3]基礎(chǔ)上,可以求出第j階振型整體結(jié)構(gòu)的等效阻尼比:

式中ξs為鋼結(jié)構(gòu)阻尼比,取為0.01;ξc為鋼筋混凝土結(jié)構(gòu)阻尼比,取為0.05;[K]s、[K]c分別為鋼結(jié)構(gòu)與混凝土的阻尼剛度矩陣,[K]為結(jié)構(gòu)整體剛度矩陣,{φ}j為第j階振型向量。
表1為前12階振型結(jié)構(gòu)等效阻尼比計算結(jié)果。可以看出,在前10階振型中,由于廠房鋼結(jié)構(gòu)組成部分振動較大,阻尼比接近鋼結(jié)構(gòu)的阻尼比。在第11、12階振型中,汽輪機(jī)鋼筋混凝土平臺與廠房鋼結(jié)構(gòu)的振動均較大,阻尼比更加接近于鋼結(jié)構(gòu)與混凝土結(jié)構(gòu)阻尼比的平均值。

表1 常規(guī)島主廠房結(jié)構(gòu)等效阻尼比Tab.1 Equivalent damping ratio of main powerhouse
2 常規(guī)島主廠房的表面風(fēng)壓
剛性模型風(fēng)洞試驗在石家莊鐵道大學(xué)風(fēng)洞試驗室完成,該風(fēng)洞低速段斷面為4 m×3 m,采用粗糙元和尖劈模擬A、B類地貌。測壓模型的縮尺比為1∶100,表面共布置496個測點,模擬0°~360°風(fēng)向角的情況,其角度間隔為15°,共24個試驗風(fēng)向角,試驗時采樣頻率為300 Hz。試驗?zāi)P筒贾门c風(fēng)洞試驗分別見圖4與圖5。

圖4 常規(guī)島主廠房試驗?zāi)P筒贾肍ig.4 Location of test model of main powerhouse for wind tunnel test

圖5 常規(guī)島主廠房風(fēng)洞試驗Fig.5 Wind tunnel test of main powerhouse

圖6 135°風(fēng)向角下屋蓋體型系數(shù)Fig.6 Contour of the shape coefficient at the wind direction 135°

圖7 135°風(fēng)向角下屋蓋極值風(fēng)吸力Fig.7 Contour of the minimum wind pressure at the wind direction 135°
對風(fēng)洞試驗數(shù)據(jù)進(jìn)行處理可以得到結(jié)構(gòu)的體型系數(shù),圖6為A類地貌,135°風(fēng)向角下屋蓋的體型系數(shù),從圖中可以看出,由于受廠房角部和女兒墻的影響,來流發(fā)生分離,屋蓋迎風(fēng)面端部的平均風(fēng)壓較大,而在遠(yuǎn)離迎風(fēng)面端部的區(qū)域,平均風(fēng)壓逐漸減小。
主廠房跨度較大,為了減輕屋蓋結(jié)構(gòu)自重,屋蓋覆面常采用輕質(zhì)材料,而屋蓋主要受風(fēng)吸力,此時覆面結(jié)構(gòu)一旦破壞,會導(dǎo)致雨雪滲漏的發(fā)生,對汽機(jī)的安全運行會有重要的影響。因此,極值風(fēng)壓的評估和計算顯得尤為重要。圖7為A類地貌135°風(fēng)向角下屋蓋圍護(hù)結(jié)構(gòu)的極值風(fēng)吸力(單位為KPa)。極值風(fēng)吸力
根據(jù)風(fēng)洞測壓數(shù)據(jù)由下式計算得到:

式中:w0為基本風(fēng)壓,為1.1 kN/m2。μs和μσ是由風(fēng)洞試驗確定的體型系數(shù)和均方跟風(fēng)壓系數(shù);μz是風(fēng)壓高度變化系數(shù);δ是峰值因子,取為3。按荷載規(guī)范[2]規(guī)定,封閉式建筑物需考慮內(nèi)壓影響,如μs為正則加0.2,如μs為負(fù)則減0.2,由于屋蓋大部分區(qū)域為負(fù)壓,μs為負(fù)減去0.2則可得到極值風(fēng)吸力。通過比較各個風(fēng)向角的極值風(fēng)吸力,確定圍護(hù)結(jié)構(gòu)的設(shè)計風(fēng)荷載。
3 常規(guī)島主廠房風(fēng)振響應(yīng)計算
根據(jù)同步測量的常規(guī)島主廠房墻面與屋蓋各測點的風(fēng)壓時程,通過傅里葉變換,由測點風(fēng)壓時程得到各個測點的荷載譜密度。然后在頻域內(nèi)對屋蓋結(jié)構(gòu)進(jìn)行風(fēng)振響應(yīng)計算[4]。
3.1 隨機(jī)位移動力響應(yīng)均方根
根據(jù)線性隨機(jī)振動理論[5],若整體結(jié)構(gòu)有限元模型有N個節(jié)點,每個節(jié)點有x,y,z三個方向的位移,則可得到第i,j階振型的廣義荷載譜:

式中:φi(k),φj(m)分別為節(jié)點k,m的第i,j階振型,,為第i,j階振型的廣義質(zhì)量;Skm(n)為節(jié)點荷載譜矩陣第k行m列的值。第i,j階振型的廣義位移協(xié)方差可由下式求得:
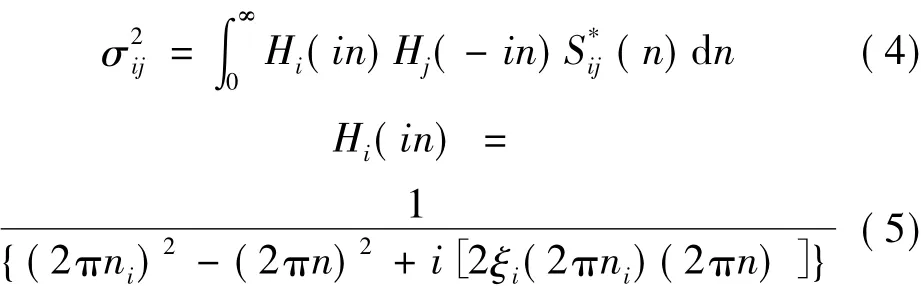

式中Hi(in)為第i振型的傳遞函數(shù),ξi為第i振型的阻尼比。
由此可得到第L個節(jié)點y軸向位移響應(yīng)均方根為:

x軸向與z軸向位移響應(yīng)均方根可按式(5)同理求得,合位移均方根可近似由下式計算:

式中:σd(L),σx(L)與σz(L)分別為節(jié)點L的合位移均方根,以及x軸向與z軸向位移響應(yīng)均方根。圖8為各風(fēng)向角下,A類地貌,在基本風(fēng)壓1.1 kN/m2作用下,計算出的常規(guī)島主廠房節(jié)點合位移均方根的最大值圖。
3.2 隨機(jī)內(nèi)力動力響應(yīng)均方根
脈動風(fēng)荷載引起的屋蓋結(jié)構(gòu)桿件內(nèi)力響應(yīng)R(z,t)可表示為:

式中:qj(t)為廣義坐標(biāo),Aj(z)為第j振型的內(nèi)力響應(yīng)函數(shù),它是結(jié)構(gòu)頻率與振型的函數(shù),特殊的當(dāng)Aj(z)為結(jié)構(gòu)節(jié)點的振型時,R(z,t)為結(jié)構(gòu)節(jié)點的位移響應(yīng)函數(shù)。Aj(z)可由下式求得:

式中,H為振型函數(shù)中最后一個節(jié)點的位置;i(z,z')為單位荷載影響函數(shù),代表z'處單位荷載引起的z處內(nèi)力。得到Aj(z)后,同樣利用下面的公式計算內(nèi)力的均方:


圖8 各風(fēng)向角下節(jié)點合位移均方根的最大值Fig.8 Maximum nodal root-mean-square total displacement under wind directions

圖9 各風(fēng)向角下桿件彎曲應(yīng)力均方根的最大值Fig.9 Maximum root-mean-square bending stress in member bar under wind directions

圖10 各風(fēng)向角下節(jié)點極值位移響應(yīng)最大值Fig.10 Maximum nodal total displacement under wind directions
圖9為各風(fēng)向角下,A類地貌,在基本風(fēng)壓1.1 kN/m2作用下,計算出的主廠房桿件彎曲應(yīng)力均方根的最大值圖。
3.3 主廠房的風(fēng)致響應(yīng)
將平均風(fēng)荷載所引起的響應(yīng)與脈動風(fēng)荷載所引起的響應(yīng)組合,可以得到結(jié)構(gòu)的極值響應(yīng):

式中:rm為平均風(fēng)壓所引起的響應(yīng),μ為動力響應(yīng)峰值因子,取為3;σr為均方根響應(yīng)值。圖10為平均風(fēng)荷載與脈動風(fēng)荷載所引起的主廠房節(jié)點合位移最大值圖。由于屋蓋處的節(jié)點位移是由豎向承重結(jié)構(gòu)的XY平面內(nèi)位移與屋蓋的Z向位移合成得到,因此各個風(fēng)向角下節(jié)點極值位移最大值發(fā)生在鋼結(jié)構(gòu)屋蓋上。
為了考察屋蓋是否滿足正常使用要求,表2給出了鋼結(jié)構(gòu)屋蓋在平均風(fēng)荷載、脈動風(fēng)荷載引起的Z軸向的位移響應(yīng),以及極值位移響應(yīng)。可以看出,屋蓋極值位移約為5 cm,滿足結(jié)構(gòu)的正常使用要求。
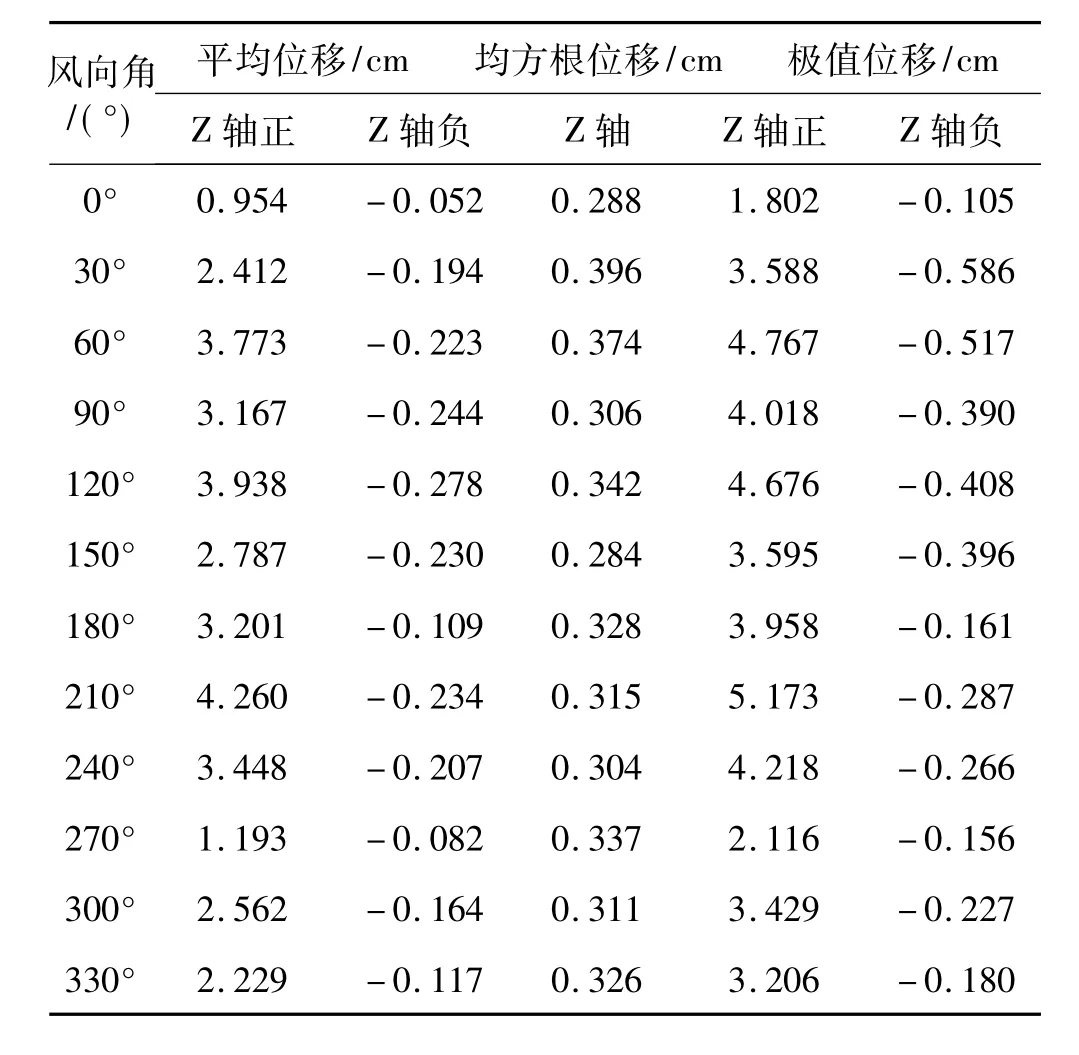
表2 主廠房鋼結(jié)構(gòu)屋蓋風(fēng)致位移響應(yīng)Tab.2 Wind-induced response of steel roof of main powerhouse
4 常規(guī)島主廠房風(fēng)振系數(shù)
國內(nèi)外學(xué)者從理論上對等效靜力風(fēng)荷載做了深入研究,但無論是陣風(fēng)荷載因子法[6,7]、慣性風(fēng)荷載法[8]還是荷載-響應(yīng)相關(guān)法[9,10],均只能求得結(jié)構(gòu)某一位置某一響應(yīng)所對應(yīng)的等效靜力風(fēng)荷載。而主廠房的構(gòu)件很多,在結(jié)構(gòu)抗風(fēng)設(shè)計和評估中,不僅需要考慮位移響應(yīng),還需考慮內(nèi)力響應(yīng),而現(xiàn)有得等效靜力風(fēng)荷載理論使用起來會很不方便。因此,本文根據(jù)風(fēng)致響應(yīng)計算結(jié)果,采用最優(yōu)化理論[11,12]來求出結(jié)構(gòu)的極值效應(yīng)等效靜力風(fēng)荷載,進(jìn)而求出風(fēng)振系數(shù)。
首先,求出結(jié)構(gòu)的節(jié)點荷載影響矩陣:

其中元素lij代表第j個節(jié)點單位力所引起的第i根桿件的響應(yīng)(內(nèi)力或者位移),然后根據(jù)前述計算結(jié)果得到的風(fēng)致極值響應(yīng)向量為:
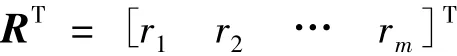
所需求解的等效靜力風(fēng)荷載向量為:

則極值效應(yīng)等效靜力風(fēng)荷載向量可由如下最小二乘問題來確定:

若要使響應(yīng)較小的桿件擬合精度高,可以采用如下的最小二乘問題來確定:
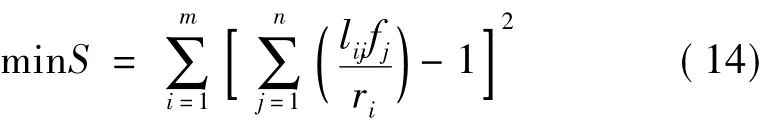

圖11 135°風(fēng)向角下主廠房風(fēng)振系數(shù)等值線Fig.11 Contour of the wind load vibration coefficient at the wind direction 135°
在得到了節(jié)點極值效應(yīng)等效靜力風(fēng)荷載后,與節(jié)點平均風(fēng)荷載相比,可得到風(fēng)振系數(shù)。圖13為在風(fēng)向角為135°情況下,根據(jù)式(12)的最小二乘格式,由前述求解得到的風(fēng)致極值內(nèi)力響應(yīng)計算結(jié)果,所確定的主廠房內(nèi)力極值相應(yīng)風(fēng)振系數(shù)等值線。
5 結(jié)論
本文在EPR常規(guī)島主廠房剛性模型風(fēng)洞試驗的基礎(chǔ)上,對表面風(fēng)荷載和風(fēng)致響應(yīng)做了計算和分析,得出如下結(jié)論:
(1)等效阻尼比計算結(jié)果反映了結(jié)構(gòu)的自振特性,主廠房的阻尼比在大部分振型中更加接近鋼結(jié)構(gòu)的阻尼比。
(2)在主廠房屋蓋的角部和端部,由于流動發(fā)生分離,且產(chǎn)生了漩渦脫落,湍流強度大,導(dǎo)致屋蓋角部和端部的平均風(fēng)壓和極值風(fēng)壓均較大。
(3)基于有限元模型和風(fēng)洞試驗得到的脈動風(fēng)荷載,在頻域內(nèi),考慮了多階振型以及振型耦合項,計算了結(jié)構(gòu)的位移和內(nèi)力風(fēng)振響應(yīng)。該計算方法適用于振型密集的結(jié)構(gòu)風(fēng)振響應(yīng)分析。
(4)根據(jù)最優(yōu)化理論,在風(fēng)致極值響應(yīng)計算結(jié)果的基礎(chǔ)上,給出了主廠房極值效應(yīng)等效靜力風(fēng)荷載和風(fēng)振系數(shù)的計算方法。該方法能夠方便的用于工程結(jié)構(gòu)的風(fēng)致響應(yīng)評估。
[1]APP-GW-GL-700. WestinghouseAP1000 design control document[R]. Westinghouse Electric Corporation LLC,2004.
[2]GB50009-2001建筑結(jié)構(gòu)荷載規(guī)范[S].北京:中國建筑工業(yè)出版社,2006.
[3] 廖振鵬.工程波動理論導(dǎo)論[M].北京:科學(xué)出版社,2002.
[4]周向陽,梁樞果,張其林.武漢體育館鋼結(jié)構(gòu)屋蓋風(fēng)振響應(yīng)分析[J].土木工程學(xué)報.2008,(41)5:33-39.
[5] Clough C W,Penzien J.Dynamic of Structures[M].New York:McGraw-Hill,INC,1993.
[6]Davenport A G.Gust loading factors[J].Journal of Structural Division.ASCE.1967,93(ST3):11-34.
[7]Davenport A G.How can we simplify and generalize wind load[J]. Journal of Wind Engineering and Industrial Aerodynamics.1995,54-55:657-669.
[8]張相庭.結(jié)構(gòu)風(fēng)壓和風(fēng)振計算[M].上海:同濟(jì)大學(xué)出版社,1985.
[9]Kasperski M,Niemann H J.The LRC(Load-responsecorrelation) method: a generalmethod ofestimation unfavorable wind load distributions for linear and non1inear structures[J].Journal of Wind Engineering and Industrial Aerodynamics.1992,43:1753 -1763.
[10] Holmes J D.Effective static load distributions in wind engineering[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90:91 -109.
[11]梁樞果,吳海洋,郭必武,等.大跨度屋蓋結(jié)構(gòu)等效靜力風(fēng)荷載數(shù)值計算方法[J].華中科技大學(xué)學(xué)報(自然科學(xué)版),2008,(36)4:110-114.
[12]席少霖,趙鳳治.最優(yōu)化計算方法[M].上海:上海科學(xué)技術(shù)出版社,1983.

