環(huán)境激勵(lì)下基礎(chǔ)隔震結(jié)構(gòu)的主要?jiǎng)恿μ匦匝芯?/h1>
2011-02-13 11:55:24韓建平王洪濤劉云帥杜永峰
振動(dòng)與沖擊 2011年11期
韓建平,王洪濤,劉云帥,杜永峰,李 慧
(1.蘭州理工大學(xué) 防震減災(zāi)研究所,蘭州 730050;2.甘肅省土木工程防災(zāi)減災(zāi)重點(diǎn)實(shí)驗(yàn)室,蘭州 730050)
基礎(chǔ)隔震作為一項(xiàng)成熟的被動(dòng)控制技術(shù),已得到了大量的應(yīng)用推廣,其良好的隔震性能也已經(jīng)得到了實(shí)際強(qiáng)震的考驗(yàn)。汶川地震中,在鄰近普通磚混結(jié)構(gòu)房屋普遍墻體開(kāi)裂的情況下,采用基礎(chǔ)隔震技術(shù)的甘肅省隴南市武都區(qū)北山郵政職工住宅樓上部結(jié)構(gòu)及隔震層下的下部支承體系完好無(wú)損[1]。
按現(xiàn)行規(guī)范規(guī)定,計(jì)算基礎(chǔ)隔震結(jié)構(gòu)的水平向減震系數(shù)時(shí),應(yīng)取剪切變形100%對(duì)應(yīng)的等效剛度和等效黏滯阻尼比;罕遇地震驗(yàn)算時(shí),宜采用剪切變形250%時(shí)的等效剛度和等效黏滯阻尼比,當(dāng)隔震支座直徑較大時(shí)可采用剪切變形100%時(shí)的等效剛度和等效黏滯阻尼比[2]。但當(dāng)結(jié)構(gòu)遭受環(huán)境激勵(lì)或較低水平的地震動(dòng)影響時(shí),隔震支座的剪切變形遠(yuǎn)遠(yuǎn)達(dá)不到設(shè)計(jì)時(shí)的水平,從而使得隔震支座的剛度及結(jié)構(gòu)的動(dòng)力特性與設(shè)計(jì)時(shí)有較大的不同。因此,有必要對(duì)基礎(chǔ)隔震結(jié)構(gòu)在微幅環(huán)境激勵(lì)下的動(dòng)力特性及參數(shù)進(jìn)行研究,這將有助于更全面地掌握其在微幅激勵(lì)作用下的響應(yīng)特點(diǎn)。目前在這方面的研究尚少,還沒(méi)有一些非常明確的結(jié)論。
本文首先通過(guò)對(duì)兩棟基礎(chǔ)隔震建筑在環(huán)境激勵(lì)下的振動(dòng)測(cè)試,運(yùn)用隨機(jī)子空間識(shí)別法和有理分式多項(xiàng)式法分別識(shí)別了結(jié)構(gòu)的模態(tài)頻率、振型和模態(tài)阻尼比。進(jìn)一步以其中一棟為研究對(duì)象,以識(shí)別的模態(tài)參數(shù)作為修正基準(zhǔn),采用多目標(biāo)優(yōu)化的方法反演了環(huán)境激勵(lì)下隔震層的實(shí)際水平等效剛度。最后基于反演的實(shí)際隔震層水平等效剛度對(duì)結(jié)構(gòu)的初始有限元模型進(jìn)行了修正,并對(duì)修正后的模型進(jìn)行了進(jìn)一步的分析。
1 基礎(chǔ)隔震建筑概況及初始有限元模型
本文測(cè)試的兩棟基礎(chǔ)隔震建筑均位于蘭州市,一棟為新建的某小學(xué)四層公共教學(xué)樓,另一棟為已建的某大學(xué)書(shū)院六層綜合教學(xué)樓。
限于篇幅,本文主要對(duì)某小學(xué)公共教學(xué)樓的概況及隔震層的布置進(jìn)行簡(jiǎn)要描述。該教學(xué)樓上部結(jié)構(gòu)為四層鋼筋混凝土框架結(jié)構(gòu),總高度15.6 m,一、二層層高為2.7 m,三層大部分為傾斜樓蓋,標(biāo)高區(qū)間為[10.2 11.4]m。該建筑的整體外觀如圖1照片所示,疊層橡膠隔震支座節(jié)點(diǎn)細(xì)部如圖2照片所示。
該建筑的隔震支座布置如圖3所示,圖中①、②、③ 分別對(duì)應(yīng) GZY400、GZY500、GZP600型隔震支座。隔震支座的規(guī)格、數(shù)量及具體參數(shù)如表1所示,其中γ為隔震支座的剪切變形,Kj和ξj分別為相應(yīng)剪切變形下隔震支座的水平等效剛度和等效黏滯阻尼比。
測(cè)試前,為了保證結(jié)構(gòu)現(xiàn)場(chǎng)測(cè)試數(shù)據(jù)的質(zhì)量,分別建立了所測(cè)試結(jié)構(gòu)隔震前和隔震后的初始有限元模型,并對(duì)其進(jìn)行了初步的動(dòng)力特性分析。

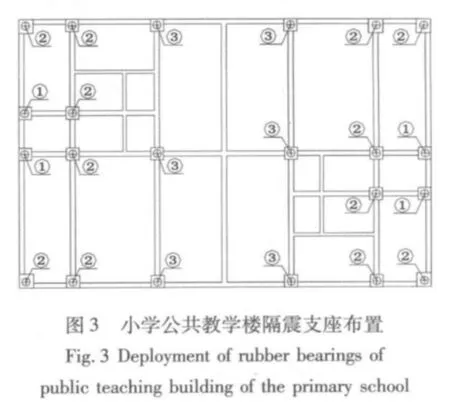
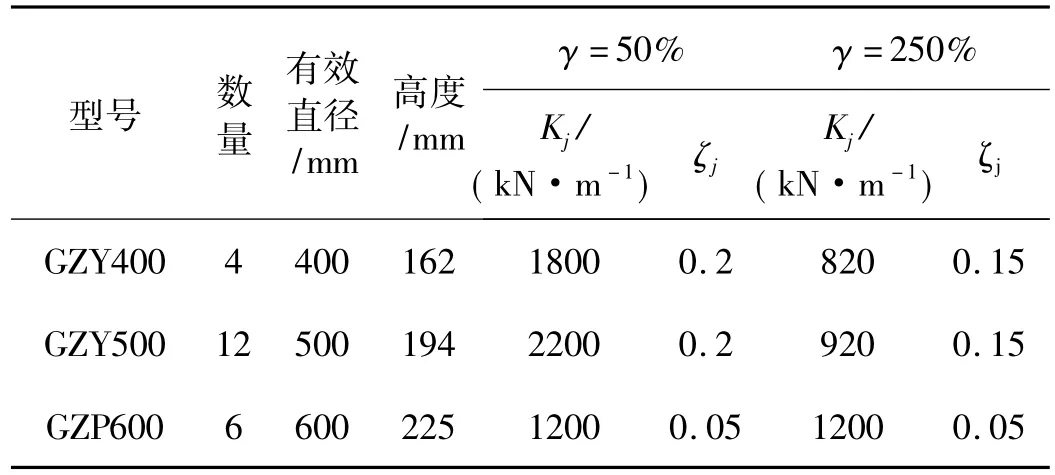
表1 隔震支座的主要參數(shù)Tab.1 Main Parameters of rubber bearings
建模過(guò)程中作了如下的假定及簡(jiǎn)化:
(1)結(jié)構(gòu)的質(zhì)量都集中在各樓層水平面上;
(2)樓板在自身平面內(nèi)剛度無(wú)限大;
(3)考慮到隔震層在小幅環(huán)境振動(dòng)激勵(lì)下達(dá)不到設(shè)計(jì)剪切變形,隔震層的等效水平剛度初步取為多遇地震設(shè)計(jì)水平等效剛度的10倍[3];
(4)將基礎(chǔ)隔震支座模擬成有橫向剛度和豎向剛度的線單元;
(5)考慮填充墻的剛度貢獻(xiàn),取周期折減系數(shù)為0.7。
依據(jù)初始有限元模型分析所得的前三階模態(tài)頻率及振型形態(tài)如表2所示。
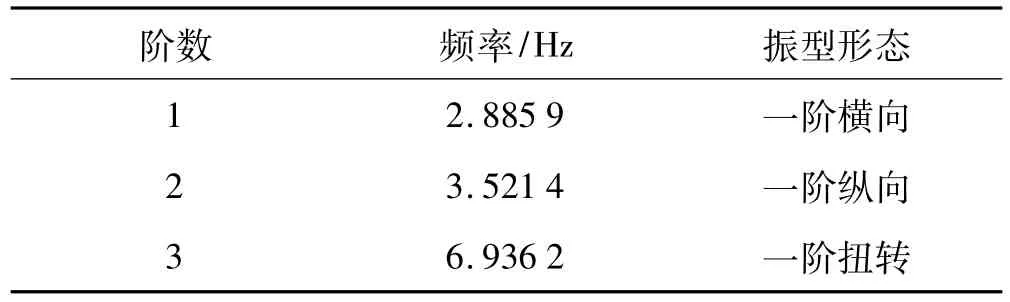
表2 初始有限元模型分析所得的前三階振型Tab.2 First 3 modes from the initial finite element model
2 環(huán)境激勵(lì)下的動(dòng)力測(cè)試
為盡可能地獲取結(jié)構(gòu)的橫向、縱向和扭轉(zhuǎn)模態(tài),每層布置四個(gè)單向水平加速度傳感器,在屋面分別設(shè)置橫、縱向兩個(gè)參考點(diǎn)。該小學(xué)綜合教學(xué)樓各層測(cè)點(diǎn)及參考點(diǎn)的布置如圖4所示。

圖4 小學(xué)公共教學(xué)樓測(cè)點(diǎn)及參考點(diǎn)布置Fig.4 Locations of traveling and reference accelerometers of public teaching building of the primary school
環(huán)境振動(dòng)下動(dòng)力測(cè)試的基本假設(shè)是使引起振動(dòng)的輸入在感興趣的頻率范圍內(nèi)具有白噪聲的特性[4]。為了滿足這一要求,需盡量減少一些外部因素比如車(chē)輛、人員、風(fēng)、機(jī)器等對(duì)結(jié)構(gòu)引起的誘使模態(tài),因此選擇在相對(duì)較安靜的深夜進(jìn)行測(cè)試。
測(cè)試使用12通道的DASP信號(hào)采集和分析系統(tǒng),采樣頻率取為80 Hz,采樣時(shí)間取為20 min,整個(gè)建筑的動(dòng)力測(cè)試共分5組。
3 模態(tài)參數(shù)的識(shí)別和分析
模態(tài)參數(shù)識(shí)別的時(shí)域方法和頻域方法各有其優(yōu)缺點(diǎn)。環(huán)境激勵(lì)下,頻域法使用的是頻響函數(shù),雖然輸入未知,但是輸入為白噪聲激勵(lì)的假定使得可由響應(yīng)的自功率譜來(lái)近似替代頻響函數(shù);時(shí)域法的初始輸入數(shù)據(jù)是系統(tǒng)的自由衰減響應(yīng)或脈沖響應(yīng),可以通過(guò)隨機(jī)減量技術(shù)或者自然激勵(lì)技術(shù)得到。從識(shí)別效果上知,時(shí)域法無(wú)法直接判別是否識(shí)別出了系統(tǒng)的所有模態(tài);而頻域法雖然可以直觀判斷模態(tài)數(shù)量,但是其阻尼比和振型的識(shí)別精度較差[5]。
為了增加識(shí)別結(jié)果的可信度,分別采用時(shí)域內(nèi)的隨機(jī)子空間法(Stochastic Subspace Identification,SSI)和頻域內(nèi)的有理分式多項(xiàng)式法(Rational Fraction Polynomial,RFP)獨(dú)立地進(jìn)行參數(shù)識(shí)別以對(duì)識(shí)別結(jié)果進(jìn)行交叉驗(yàn)證[6,7]。
3.1 參數(shù)識(shí)別
模態(tài)參數(shù)識(shí)別時(shí),選用白噪聲激勵(lì)下各測(cè)點(diǎn)縱、橫向的數(shù)據(jù),其中,SSI法的Hankel矩陣采用方陣構(gòu)造,系統(tǒng)定階采用文獻(xiàn)[7]中的方法;為解決擬合漏階的問(wèn)題,RFP法采用頻響函數(shù)虛部歸一化向量權(quán)函數(shù)進(jìn)行擬合識(shí)別。模態(tài)參數(shù)識(shí)別結(jié)果見(jiàn)表3所示,前三階振型如圖5所示。
利用模態(tài)置信準(zhǔn)則(Modal Assurance Criterion,MAC)[8]評(píng)價(jià)SSI和RFP兩種方法識(shí)別結(jié)果的相關(guān)性,計(jì)算結(jié)果見(jiàn)表3所示。兩種方法識(shí)別的各階振型的MAC值均在0.75以上,表明兩種方法的識(shí)別結(jié)果有較好的相關(guān)性。
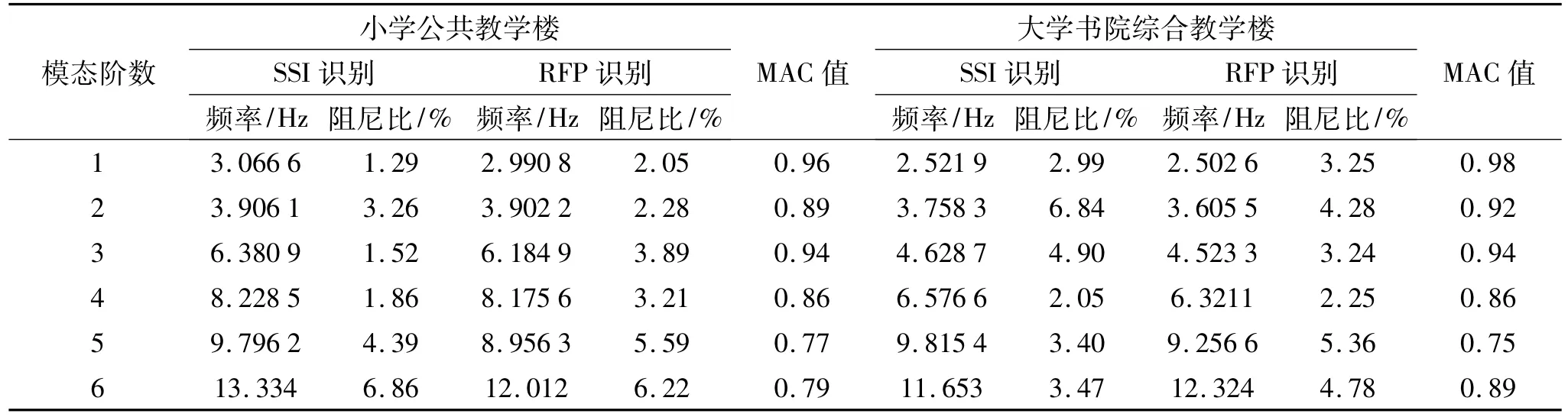
表3 模態(tài)參數(shù)識(shí)別結(jié)果Tab.3 Identified results of modal parameters
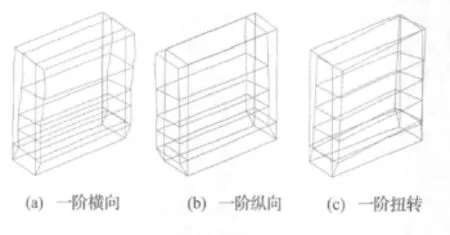
圖5 實(shí)測(cè)所得的小學(xué)公共教學(xué)樓前三階振型Fig.5 Identified first 3 mode shapes of public teaching building of the primary school
3.2 有關(guān)阻尼識(shí)別結(jié)果的討論
一般認(rèn)為,在基礎(chǔ)隔震結(jié)構(gòu)中,由于隔震系統(tǒng)與上部結(jié)構(gòu)的阻尼特性截然不同,它們所組成的整體是典型的非比例阻尼體系[9]。但表3結(jié)果表明,在環(huán)境激勵(lì)下,盡管RFP方法識(shí)別的阻尼比結(jié)果整體略大于SSI方法的識(shí)別結(jié)果,但兩種方法識(shí)別所得的隔震結(jié)構(gòu)前三階振型的阻尼比都相對(duì)較小。基礎(chǔ)隔震結(jié)構(gòu)的等效黏滯阻尼比的大小近乎于未隔震結(jié)構(gòu)的阻尼比,主要是由于隔震支座在低水平的環(huán)境振動(dòng)激勵(lì)下,由橫向振動(dòng)所引起的位移和應(yīng)變都很小,變形橡膠層中的能量損失較小,隔震層對(duì)整體結(jié)構(gòu)的阻尼貢獻(xiàn)較小[4]。
本次測(cè)試中,隔震支座支墩頂部測(cè)點(diǎn)與一層樓面處對(duì)應(yīng)測(cè)點(diǎn)記錄的短向速度時(shí)程如圖6所示,從中提取的主要時(shí)域指標(biāo)見(jiàn)表4。綜合圖6及表4結(jié)果,兩個(gè)測(cè)點(diǎn)處的速度絕對(duì)值都較小,且隔震支座的相對(duì)速度值也較小,因此隔震支座提供的阻尼也必然較小。
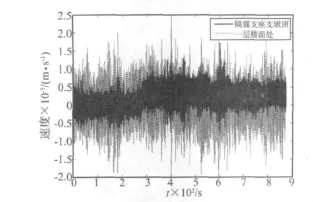
圖6 隔震支座上下速度時(shí)程圖Fig.6 Velocity time history at top and bottom of a rubber bearing

表4 隔震支座上下速度記錄的時(shí)域統(tǒng)計(jì)指標(biāo)Tab.4 Time domain statistics of velocity record at top and bottom of a rubber bearing
隔震結(jié)構(gòu)在環(huán)境激勵(lì)下未表現(xiàn)出隔震層的高柔性和大阻尼,雖然隔震系統(tǒng)與上部結(jié)構(gòu)的阻尼機(jī)制不同,但在環(huán)境激勵(lì)下兩者表現(xiàn)出來(lái)的阻尼特性沒(méi)有太大的不同,因此本文在后續(xù)分析中將環(huán)境激勵(lì)下的基礎(chǔ)隔震結(jié)構(gòu)視為比例阻尼體系。
另外要說(shuō)明的是,結(jié)合表3中阻尼的識(shí)別結(jié)果以及作者以前所做的一些工作,要比較精準(zhǔn)地識(shí)別模態(tài)阻尼比仍然是比較困難的。對(duì)基礎(chǔ)隔震結(jié)構(gòu),阻尼的精確識(shí)別對(duì)研究隔震支座的耗能機(jī)制、隔震結(jié)構(gòu)的非比例阻尼問(wèn)題等是非常重要的,因此仍然是一個(gè)需要進(jìn)一步研究的問(wèn)題。國(guó)外一些學(xué)者提出的瞬時(shí)阻尼、阻尼譜[10,11]等一些阻尼識(shí)別的新思想,對(duì)基礎(chǔ)隔震結(jié)構(gòu)阻尼的識(shí)別有一定的參考意義。
4 環(huán)境激勵(lì)下隔震層實(shí)際水平等效剛度的反演
為了研究隔震支座在小幅環(huán)境激勵(lì)下的剛度與設(shè)計(jì)剛度取值的不同及其對(duì)結(jié)構(gòu)動(dòng)力特性的影響,也為了進(jìn)一步修正初始有限元模型以使其可以更好地反映環(huán)境激勵(lì)下基礎(chǔ)隔震結(jié)構(gòu)的動(dòng)力特性及響應(yīng),準(zhǔn)確、合理地確定隔震層的水平等效剛度是非常重要的。
本文基于環(huán)境激勵(lì)下的實(shí)測(cè)結(jié)果,采用多目標(biāo)優(yōu)化的方法來(lái)反演環(huán)境激勵(lì)下隔震層的水平等效剛度。
鑒于前述有關(guān)環(huán)境激勵(lì)下隔震結(jié)構(gòu)阻尼特性的討論,采用具有經(jīng)典比例阻尼的層間剪切模型代表研究的基礎(chǔ)隔震結(jié)構(gòu)。假定同層各構(gòu)件的水平位移一致,忽略柱的軸向變形;將首層下半部分墻體的質(zhì)量和隔震層的質(zhì)量集中到隔震支座頂部的樓板上,其它層墻體的質(zhì)量分別集中于各層樓板及屋面板。
在環(huán)境激勵(lì)下基礎(chǔ)隔震結(jié)構(gòu)的運(yùn)動(dòng)微分方程為:
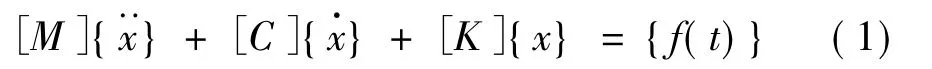
式中[K]、[M]和[C]分別為層間剪切型模型的剛度矩陣、質(zhì)量矩陣和阻尼矩陣;{f(t)}為隨機(jī)的環(huán)境激勵(lì)。
對(duì)無(wú)阻尼自由振動(dòng)體系進(jìn)行頻率和振型計(jì)算后,選取前三階實(shí)測(cè)頻率與計(jì)算頻率的差的平方和及振型模態(tài)置信準(zhǔn)則(MAC)的負(fù)值為目標(biāo)函數(shù),建立多目標(biāo)優(yōu)化識(shí)別隔震層水平等效剛度的數(shù)學(xué)模型如下:
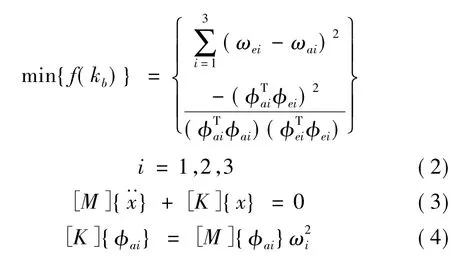
式中ωei和φei分別為環(huán)境激勵(lì)下實(shí)測(cè)所得的結(jié)構(gòu)第i階頻率和振型向量;ωai和φai分別為無(wú)阻尼層間剪切模型計(jì)算所得的第i階頻率和振型向量。
式(3)和式(4)中的[K]和[M]分別取如下的表達(dá)式:

其中kb、mb分別為隔震層的等效水平剛度和集中質(zhì)量;ki、mi分別為第i層(i=1,2,3,4)的層間側(cè)移剛度和集中質(zhì)量。
為了判斷目標(biāo)函數(shù)的總體優(yōu)化效果,利用線性加權(quán)和的方法,分別給表征前三階模態(tài)實(shí)測(cè)頻率與計(jì)算頻率差值的平方及各階MAC的負(fù)值乘以權(quán)系數(shù)γi(i=1,2,3),將式(2)中的目標(biāo)函數(shù)改寫(xiě)為如下形式,則多目標(biāo)優(yōu)化問(wèn)題轉(zhuǎn)化為一維的單目標(biāo)優(yōu)化問(wèn)題[12]。
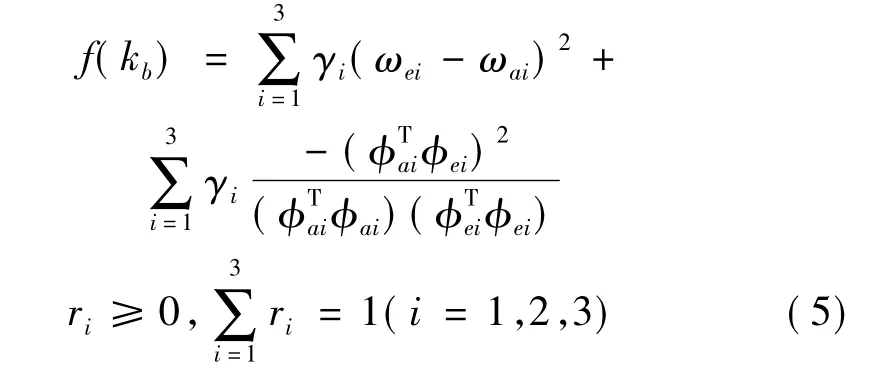
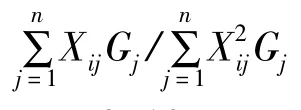
該優(yōu)化問(wèn)題采用經(jīng)典0.618法求解最優(yōu)的kb值。
本文討論的結(jié)構(gòu)隔震層在多遇地震設(shè)計(jì)水平等效剛度為40 800 kN/m,結(jié)合前面的假定,迭代初始區(qū)間[kb1,kb2]取為[0.3,0.5]×106kN/m,收斂容差 ε 取0.01。
經(jīng)迭代計(jì)算,得出在環(huán)境激勵(lì)下隔震層的實(shí)際水平等效剛度kb=444 720 kN/m,其值為多遇地震設(shè)計(jì)時(shí)所取水平等效剛度的10.9倍,另外該值也大于結(jié)構(gòu)第三層和第四層的層間剪切剛度值。
環(huán)境激勵(lì)下及不同隔震支座剪切變形時(shí)基礎(chǔ)隔震結(jié)構(gòu)的動(dòng)力特性對(duì)比見(jiàn)表5。
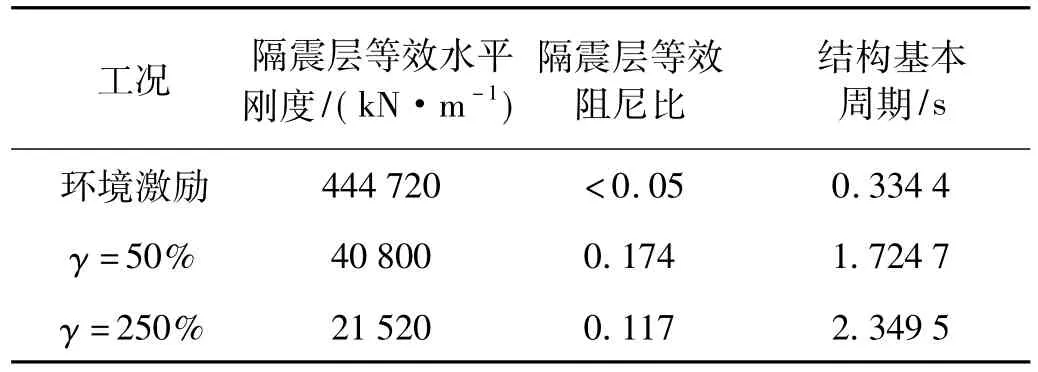
表5 隔震結(jié)構(gòu)動(dòng)力參數(shù)隨隔震支座不同剪切變形的變化Tab.5 Dynamic parameters of base-isolated structure with different shear deformation of rubber bearings
表5表明,不同振動(dòng)幅值時(shí)隔震層的等效水平剛度和等效黏滯阻尼比相差較大,結(jié)構(gòu)體系的基本周期相應(yīng)地也有較大變化。
值得注意的是該建筑設(shè)計(jì)計(jì)算階段所得的隔震前基本周期為0.460 4 s,大于在環(huán)境激勵(lì)下實(shí)測(cè)的隔震后周期值0.334 4 s,這固然與隔震層在環(huán)境激勵(lì)下剛度較大有關(guān)系,另外理論建模與實(shí)際施工之間的差異以及理論建模是否能考慮影響結(jié)構(gòu)動(dòng)力特性的所有主要因素也是值得進(jìn)一步研究的。
隔震層在微幅振動(dòng)激勵(lì)下的水平等效剛度很大,從結(jié)構(gòu)抗風(fēng)角度來(lái)講是合理的,可以保證隔震建筑在風(fēng)振激勵(lì)下的舒適性能。
5 基于反演隔震層水平剛度的有限元模型修正
將反演所得的隔震層等效水平剛度反饋到初始有限元模型,得到修正后的有限元模型。依據(jù)修正后的有限元模型分析所得的前三階振型的頻率及其與試驗(yàn)識(shí)別結(jié)果及初始有限元分析結(jié)果的對(duì)比如表6所示。修正后的前三階振型如圖7所示。
表6結(jié)果及圖5和圖7的對(duì)比表明,修正后的有限元模型分析所得的頻率與試驗(yàn)識(shí)別得到的頻率吻合較好,兩者的振型形狀也基本相似,前三階的MAC值都在0.88以上,表明計(jì)算振型與實(shí)測(cè)振型之間有較好的相關(guān)性[13]。

表6 修正前后前三階模態(tài)頻率與識(shí)別頻率的對(duì)比及修正后分析模態(tài)與識(shí)別模態(tài)的MACTab.6 Comparison of first 3 frequencies from ambient vibration test,initial model,updated model and MACs between updated modes and identified modes

圖7 修正后有限元模型分析所得的前三階振型Fig.7 First 3 mode shapes from updated finite element model
6 結(jié)論
對(duì)兩棟基礎(chǔ)隔震建筑在環(huán)境激勵(lì)下的動(dòng)力測(cè)試及模態(tài)參數(shù)的識(shí)別結(jié)果表明,環(huán)境激勵(lì)下基礎(chǔ)隔震結(jié)構(gòu)的動(dòng)力性能與設(shè)計(jì)分析階段所考慮的動(dòng)力性能差別很大,結(jié)構(gòu)的基本周期和模態(tài)阻尼比均遠(yuǎn)小于多遇地震和罕遇地震設(shè)計(jì)工況下的相應(yīng)值。因此,為了進(jìn)一步研究基礎(chǔ)隔震結(jié)構(gòu)在環(huán)境激勵(lì)下的動(dòng)力性能,選擇其中一棟為研究對(duì)象,利用多目標(biāo)優(yōu)化的方法反演分析了隔震層在環(huán)境激勵(lì)下的實(shí)際水平等效剛度,反演所得的隔震層水平等效剛度為多遇地震工況下計(jì)算剛度取值的10.9倍。最后基于反演的實(shí)際隔震層水平等效剛度對(duì)結(jié)構(gòu)的初始有限元模型進(jìn)行了修正,修正后模型的數(shù)值分析結(jié)果與實(shí)際測(cè)試結(jié)果的對(duì)比表明,修正后的模型可以更好地反映結(jié)構(gòu)在環(huán)境激勵(lì)下的動(dòng)力特性。
另外,測(cè)試分析結(jié)果也表明,識(shí)別所得的隔震結(jié)構(gòu)前三階振型的阻尼比都相對(duì)較小,基礎(chǔ)隔震結(jié)構(gòu)的等效黏滯阻尼比的大小近乎于未隔震結(jié)構(gòu)的阻尼比,因此,隔震層對(duì)整體結(jié)構(gòu)的阻尼貢獻(xiàn)較小,在環(huán)境激勵(lì)等微幅振動(dòng)影響下,基礎(chǔ)隔震結(jié)構(gòu)可以視為經(jīng)典的比例阻尼系統(tǒng)。
[1]莫 庸,金建民,杜永峰,等.高烈度地震區(qū)建筑結(jié)構(gòu)選型問(wèn)題的初步探討——5.12汶川大地震隴南地區(qū)建筑結(jié)構(gòu)震害考察中結(jié)構(gòu)選型問(wèn)題的思考[J].工程抗震與加固改造,2008,30(4):50-55.
[2]GB50011-2010.建筑抗震設(shè)計(jì)規(guī)范[S].北京:中國(guó)建筑工業(yè)出版社,2010.
[3]Skinner R I,Robinson W H,Mcverry G H.工程隔震概論[M].謝禮立,周雍年,趙興權(quán),譯.北京:地震出版社,1996.
[4] Ventura C E,F(xiàn)inn W D L,Lord J F,et al.Dynamic characteristics of a base isolated building from ambient vibration measurements and low level earthquake shaking[J].Soil Dynamics and Earthquake Engineering,2003,23(4):313-322.
[5]Han J P,Lu X L,Wang F X.Comparison of modal parameter identification algorithms based on shaking table model test data[C]//The International Society for Optical Engineering,2009:73750K-1-7.
[6]Overschee P V,Moor B D.Subspace identification for linear systems: theory, implementation, applications[M].Dordrecht:Kluwer Academic Publishers,1996.
[7] Juang J N.Applied system identification[M].Englewood Cliffs:Prentice-Hall Inc,1994.
[8] Allemang R J,Brown D L.A correlation coefficient for modal vector analysis[C].Proceedings of the First International Modal Analysis Conference (IMAC), Orlando,F(xiàn)lorida;1982.
[9]杜永峰,李 慧,Spencer B F,等.非比例阻尼隔震結(jié)構(gòu)地震響應(yīng)的實(shí)振型分解法[J].工程力學(xué),2003,20(4):24-32.
[10] Pines D,Salvino L.Structural health monitoring using empirical mode decomposition and the Hilbert phase[J].Journal of Sound and Vibration,2006,294(1-2):97-124.
[11] Ceravolo R.Use of instantaneous estimators for the evaluation of structural damping[J].Journal of Sound and Vibration,2004:385-401.
[12]明圖章,胡光偉,黃 衛(wèi).大跨徑鋼橋面鋪裝體系多目標(biāo)優(yōu)化設(shè)計(jì)[J].土木工程學(xué)報(bào),2007,40(2):70-73.
[13]任偉新,彭雪林.青洲斜拉橋的基準(zhǔn)動(dòng)力有限元模型[J].計(jì)算力學(xué)學(xué)報(bào),2007,24(5):609-613.
猜你喜歡
長(zhǎng)期鍛煉創(chuàng)造體內(nèi)抑癌環(huán)境中老年保健(2021年12期)2021-08-24 03:30:40 一種用于自主學(xué)習(xí)的虛擬仿真環(huán)境中國(guó)傳媒大學(xué)學(xué)報(bào)(自然科學(xué)版)(2021年1期)2021-06-09 08:43:00 孕期遠(yuǎn)離容易致畸的環(huán)境中國(guó)生殖健康(2020年6期)2020-02-01 06:28:50 環(huán)境中國(guó)生殖健康(2019年11期)2019-01-07 01:28:02 國(guó)內(nèi)多模態(tài)教學(xué)研究回顧與展望湖北經(jīng)濟(jì)學(xué)院學(xué)報(bào)·人文社科版(2015年8期)2015-12-29 05:53:07 基于HHT和Prony算法的電力系統(tǒng)低頻振蕩模態(tài)識(shí)別上海電機(jī)學(xué)院學(xué)報(bào)(2015年4期)2015-02-28 14:30:00 磨削淬硬殘余應(yīng)力的有限元分析機(jī)械工程師(2015年10期)2015-02-02 01:14:03 由單個(gè)模態(tài)構(gòu)造對(duì)稱簡(jiǎn)支梁的抗彎剛度計(jì)算物理(2014年2期)2014-03-11 17:01:39 基于SolidWorks的吸嘴支撐臂有限元分析機(jī)電產(chǎn)品開(kāi)發(fā)與創(chuàng)新(2014年4期)2014-03-11 16:42:24 箱形孔軋制的有限元模擬上海金屬(2013年4期)2013-12-20 07:57:18
韓建平,王洪濤,劉云帥,杜永峰,李 慧
(1.蘭州理工大學(xué) 防震減災(zāi)研究所,蘭州 730050;2.甘肅省土木工程防災(zāi)減災(zāi)重點(diǎn)實(shí)驗(yàn)室,蘭州 730050)
基礎(chǔ)隔震作為一項(xiàng)成熟的被動(dòng)控制技術(shù),已得到了大量的應(yīng)用推廣,其良好的隔震性能也已經(jīng)得到了實(shí)際強(qiáng)震的考驗(yàn)。汶川地震中,在鄰近普通磚混結(jié)構(gòu)房屋普遍墻體開(kāi)裂的情況下,采用基礎(chǔ)隔震技術(shù)的甘肅省隴南市武都區(qū)北山郵政職工住宅樓上部結(jié)構(gòu)及隔震層下的下部支承體系完好無(wú)損[1]。
按現(xiàn)行規(guī)范規(guī)定,計(jì)算基礎(chǔ)隔震結(jié)構(gòu)的水平向減震系數(shù)時(shí),應(yīng)取剪切變形100%對(duì)應(yīng)的等效剛度和等效黏滯阻尼比;罕遇地震驗(yàn)算時(shí),宜采用剪切變形250%時(shí)的等效剛度和等效黏滯阻尼比,當(dāng)隔震支座直徑較大時(shí)可采用剪切變形100%時(shí)的等效剛度和等效黏滯阻尼比[2]。但當(dāng)結(jié)構(gòu)遭受環(huán)境激勵(lì)或較低水平的地震動(dòng)影響時(shí),隔震支座的剪切變形遠(yuǎn)遠(yuǎn)達(dá)不到設(shè)計(jì)時(shí)的水平,從而使得隔震支座的剛度及結(jié)構(gòu)的動(dòng)力特性與設(shè)計(jì)時(shí)有較大的不同。因此,有必要對(duì)基礎(chǔ)隔震結(jié)構(gòu)在微幅環(huán)境激勵(lì)下的動(dòng)力特性及參數(shù)進(jìn)行研究,這將有助于更全面地掌握其在微幅激勵(lì)作用下的響應(yīng)特點(diǎn)。目前在這方面的研究尚少,還沒(méi)有一些非常明確的結(jié)論。
本文首先通過(guò)對(duì)兩棟基礎(chǔ)隔震建筑在環(huán)境激勵(lì)下的振動(dòng)測(cè)試,運(yùn)用隨機(jī)子空間識(shí)別法和有理分式多項(xiàng)式法分別識(shí)別了結(jié)構(gòu)的模態(tài)頻率、振型和模態(tài)阻尼比。進(jìn)一步以其中一棟為研究對(duì)象,以識(shí)別的模態(tài)參數(shù)作為修正基準(zhǔn),采用多目標(biāo)優(yōu)化的方法反演了環(huán)境激勵(lì)下隔震層的實(shí)際水平等效剛度。最后基于反演的實(shí)際隔震層水平等效剛度對(duì)結(jié)構(gòu)的初始有限元模型進(jìn)行了修正,并對(duì)修正后的模型進(jìn)行了進(jìn)一步的分析。
1 基礎(chǔ)隔震建筑概況及初始有限元模型
本文測(cè)試的兩棟基礎(chǔ)隔震建筑均位于蘭州市,一棟為新建的某小學(xué)四層公共教學(xué)樓,另一棟為已建的某大學(xué)書(shū)院六層綜合教學(xué)樓。
限于篇幅,本文主要對(duì)某小學(xué)公共教學(xué)樓的概況及隔震層的布置進(jìn)行簡(jiǎn)要描述。該教學(xué)樓上部結(jié)構(gòu)為四層鋼筋混凝土框架結(jié)構(gòu),總高度15.6 m,一、二層層高為2.7 m,三層大部分為傾斜樓蓋,標(biāo)高區(qū)間為[10.2 11.4]m。該建筑的整體外觀如圖1照片所示,疊層橡膠隔震支座節(jié)點(diǎn)細(xì)部如圖2照片所示。
該建筑的隔震支座布置如圖3所示,圖中①、②、③ 分別對(duì)應(yīng) GZY400、GZY500、GZP600型隔震支座。隔震支座的規(guī)格、數(shù)量及具體參數(shù)如表1所示,其中γ為隔震支座的剪切變形,Kj和ξj分別為相應(yīng)剪切變形下隔震支座的水平等效剛度和等效黏滯阻尼比。
測(cè)試前,為了保證結(jié)構(gòu)現(xiàn)場(chǎng)測(cè)試數(shù)據(jù)的質(zhì)量,分別建立了所測(cè)試結(jié)構(gòu)隔震前和隔震后的初始有限元模型,并對(duì)其進(jìn)行了初步的動(dòng)力特性分析。



表1 隔震支座的主要參數(shù)Tab.1 Main Parameters of rubber bearings
建模過(guò)程中作了如下的假定及簡(jiǎn)化:
(1)結(jié)構(gòu)的質(zhì)量都集中在各樓層水平面上;
(2)樓板在自身平面內(nèi)剛度無(wú)限大;
(3)考慮到隔震層在小幅環(huán)境振動(dòng)激勵(lì)下達(dá)不到設(shè)計(jì)剪切變形,隔震層的等效水平剛度初步取為多遇地震設(shè)計(jì)水平等效剛度的10倍[3];
(4)將基礎(chǔ)隔震支座模擬成有橫向剛度和豎向剛度的線單元;
(5)考慮填充墻的剛度貢獻(xiàn),取周期折減系數(shù)為0.7。
依據(jù)初始有限元模型分析所得的前三階模態(tài)頻率及振型形態(tài)如表2所示。

表2 初始有限元模型分析所得的前三階振型Tab.2 First 3 modes from the initial finite element model
2 環(huán)境激勵(lì)下的動(dòng)力測(cè)試
為盡可能地獲取結(jié)構(gòu)的橫向、縱向和扭轉(zhuǎn)模態(tài),每層布置四個(gè)單向水平加速度傳感器,在屋面分別設(shè)置橫、縱向兩個(gè)參考點(diǎn)。該小學(xué)綜合教學(xué)樓各層測(cè)點(diǎn)及參考點(diǎn)的布置如圖4所示。

圖4 小學(xué)公共教學(xué)樓測(cè)點(diǎn)及參考點(diǎn)布置Fig.4 Locations of traveling and reference accelerometers of public teaching building of the primary school
環(huán)境振動(dòng)下動(dòng)力測(cè)試的基本假設(shè)是使引起振動(dòng)的輸入在感興趣的頻率范圍內(nèi)具有白噪聲的特性[4]。為了滿足這一要求,需盡量減少一些外部因素比如車(chē)輛、人員、風(fēng)、機(jī)器等對(duì)結(jié)構(gòu)引起的誘使模態(tài),因此選擇在相對(duì)較安靜的深夜進(jìn)行測(cè)試。
測(cè)試使用12通道的DASP信號(hào)采集和分析系統(tǒng),采樣頻率取為80 Hz,采樣時(shí)間取為20 min,整個(gè)建筑的動(dòng)力測(cè)試共分5組。
3 模態(tài)參數(shù)的識(shí)別和分析
模態(tài)參數(shù)識(shí)別的時(shí)域方法和頻域方法各有其優(yōu)缺點(diǎn)。環(huán)境激勵(lì)下,頻域法使用的是頻響函數(shù),雖然輸入未知,但是輸入為白噪聲激勵(lì)的假定使得可由響應(yīng)的自功率譜來(lái)近似替代頻響函數(shù);時(shí)域法的初始輸入數(shù)據(jù)是系統(tǒng)的自由衰減響應(yīng)或脈沖響應(yīng),可以通過(guò)隨機(jī)減量技術(shù)或者自然激勵(lì)技術(shù)得到。從識(shí)別效果上知,時(shí)域法無(wú)法直接判別是否識(shí)別出了系統(tǒng)的所有模態(tài);而頻域法雖然可以直觀判斷模態(tài)數(shù)量,但是其阻尼比和振型的識(shí)別精度較差[5]。
為了增加識(shí)別結(jié)果的可信度,分別采用時(shí)域內(nèi)的隨機(jī)子空間法(Stochastic Subspace Identification,SSI)和頻域內(nèi)的有理分式多項(xiàng)式法(Rational Fraction Polynomial,RFP)獨(dú)立地進(jìn)行參數(shù)識(shí)別以對(duì)識(shí)別結(jié)果進(jìn)行交叉驗(yàn)證[6,7]。
3.1 參數(shù)識(shí)別
模態(tài)參數(shù)識(shí)別時(shí),選用白噪聲激勵(lì)下各測(cè)點(diǎn)縱、橫向的數(shù)據(jù),其中,SSI法的Hankel矩陣采用方陣構(gòu)造,系統(tǒng)定階采用文獻(xiàn)[7]中的方法;為解決擬合漏階的問(wèn)題,RFP法采用頻響函數(shù)虛部歸一化向量權(quán)函數(shù)進(jìn)行擬合識(shí)別。模態(tài)參數(shù)識(shí)別結(jié)果見(jiàn)表3所示,前三階振型如圖5所示。
利用模態(tài)置信準(zhǔn)則(Modal Assurance Criterion,MAC)[8]評(píng)價(jià)SSI和RFP兩種方法識(shí)別結(jié)果的相關(guān)性,計(jì)算結(jié)果見(jiàn)表3所示。兩種方法識(shí)別的各階振型的MAC值均在0.75以上,表明兩種方法的識(shí)別結(jié)果有較好的相關(guān)性。

表3 模態(tài)參數(shù)識(shí)別結(jié)果Tab.3 Identified results of modal parameters

圖5 實(shí)測(cè)所得的小學(xué)公共教學(xué)樓前三階振型Fig.5 Identified first 3 mode shapes of public teaching building of the primary school
3.2 有關(guān)阻尼識(shí)別結(jié)果的討論
一般認(rèn)為,在基礎(chǔ)隔震結(jié)構(gòu)中,由于隔震系統(tǒng)與上部結(jié)構(gòu)的阻尼特性截然不同,它們所組成的整體是典型的非比例阻尼體系[9]。但表3結(jié)果表明,在環(huán)境激勵(lì)下,盡管RFP方法識(shí)別的阻尼比結(jié)果整體略大于SSI方法的識(shí)別結(jié)果,但兩種方法識(shí)別所得的隔震結(jié)構(gòu)前三階振型的阻尼比都相對(duì)較小。基礎(chǔ)隔震結(jié)構(gòu)的等效黏滯阻尼比的大小近乎于未隔震結(jié)構(gòu)的阻尼比,主要是由于隔震支座在低水平的環(huán)境振動(dòng)激勵(lì)下,由橫向振動(dòng)所引起的位移和應(yīng)變都很小,變形橡膠層中的能量損失較小,隔震層對(duì)整體結(jié)構(gòu)的阻尼貢獻(xiàn)較小[4]。
本次測(cè)試中,隔震支座支墩頂部測(cè)點(diǎn)與一層樓面處對(duì)應(yīng)測(cè)點(diǎn)記錄的短向速度時(shí)程如圖6所示,從中提取的主要時(shí)域指標(biāo)見(jiàn)表4。綜合圖6及表4結(jié)果,兩個(gè)測(cè)點(diǎn)處的速度絕對(duì)值都較小,且隔震支座的相對(duì)速度值也較小,因此隔震支座提供的阻尼也必然較小。

圖6 隔震支座上下速度時(shí)程圖Fig.6 Velocity time history at top and bottom of a rubber bearing

表4 隔震支座上下速度記錄的時(shí)域統(tǒng)計(jì)指標(biāo)Tab.4 Time domain statistics of velocity record at top and bottom of a rubber bearing
隔震結(jié)構(gòu)在環(huán)境激勵(lì)下未表現(xiàn)出隔震層的高柔性和大阻尼,雖然隔震系統(tǒng)與上部結(jié)構(gòu)的阻尼機(jī)制不同,但在環(huán)境激勵(lì)下兩者表現(xiàn)出來(lái)的阻尼特性沒(méi)有太大的不同,因此本文在后續(xù)分析中將環(huán)境激勵(lì)下的基礎(chǔ)隔震結(jié)構(gòu)視為比例阻尼體系。
另外要說(shuō)明的是,結(jié)合表3中阻尼的識(shí)別結(jié)果以及作者以前所做的一些工作,要比較精準(zhǔn)地識(shí)別模態(tài)阻尼比仍然是比較困難的。對(duì)基礎(chǔ)隔震結(jié)構(gòu),阻尼的精確識(shí)別對(duì)研究隔震支座的耗能機(jī)制、隔震結(jié)構(gòu)的非比例阻尼問(wèn)題等是非常重要的,因此仍然是一個(gè)需要進(jìn)一步研究的問(wèn)題。國(guó)外一些學(xué)者提出的瞬時(shí)阻尼、阻尼譜[10,11]等一些阻尼識(shí)別的新思想,對(duì)基礎(chǔ)隔震結(jié)構(gòu)阻尼的識(shí)別有一定的參考意義。
4 環(huán)境激勵(lì)下隔震層實(shí)際水平等效剛度的反演
為了研究隔震支座在小幅環(huán)境激勵(lì)下的剛度與設(shè)計(jì)剛度取值的不同及其對(duì)結(jié)構(gòu)動(dòng)力特性的影響,也為了進(jìn)一步修正初始有限元模型以使其可以更好地反映環(huán)境激勵(lì)下基礎(chǔ)隔震結(jié)構(gòu)的動(dòng)力特性及響應(yīng),準(zhǔn)確、合理地確定隔震層的水平等效剛度是非常重要的。
本文基于環(huán)境激勵(lì)下的實(shí)測(cè)結(jié)果,采用多目標(biāo)優(yōu)化的方法來(lái)反演環(huán)境激勵(lì)下隔震層的水平等效剛度。
鑒于前述有關(guān)環(huán)境激勵(lì)下隔震結(jié)構(gòu)阻尼特性的討論,采用具有經(jīng)典比例阻尼的層間剪切模型代表研究的基礎(chǔ)隔震結(jié)構(gòu)。假定同層各構(gòu)件的水平位移一致,忽略柱的軸向變形;將首層下半部分墻體的質(zhì)量和隔震層的質(zhì)量集中到隔震支座頂部的樓板上,其它層墻體的質(zhì)量分別集中于各層樓板及屋面板。
在環(huán)境激勵(lì)下基礎(chǔ)隔震結(jié)構(gòu)的運(yùn)動(dòng)微分方程為:
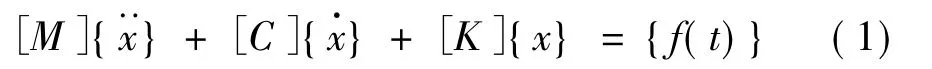
式中[K]、[M]和[C]分別為層間剪切型模型的剛度矩陣、質(zhì)量矩陣和阻尼矩陣;{f(t)}為隨機(jī)的環(huán)境激勵(lì)。
對(duì)無(wú)阻尼自由振動(dòng)體系進(jìn)行頻率和振型計(jì)算后,選取前三階實(shí)測(cè)頻率與計(jì)算頻率的差的平方和及振型模態(tài)置信準(zhǔn)則(MAC)的負(fù)值為目標(biāo)函數(shù),建立多目標(biāo)優(yōu)化識(shí)別隔震層水平等效剛度的數(shù)學(xué)模型如下:
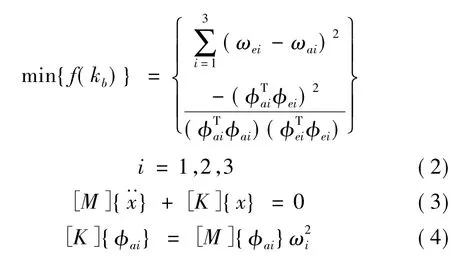
式中ωei和φei分別為環(huán)境激勵(lì)下實(shí)測(cè)所得的結(jié)構(gòu)第i階頻率和振型向量;ωai和φai分別為無(wú)阻尼層間剪切模型計(jì)算所得的第i階頻率和振型向量。
式(3)和式(4)中的[K]和[M]分別取如下的表達(dá)式:

其中kb、mb分別為隔震層的等效水平剛度和集中質(zhì)量;ki、mi分別為第i層(i=1,2,3,4)的層間側(cè)移剛度和集中質(zhì)量。
為了判斷目標(biāo)函數(shù)的總體優(yōu)化效果,利用線性加權(quán)和的方法,分別給表征前三階模態(tài)實(shí)測(cè)頻率與計(jì)算頻率差值的平方及各階MAC的負(fù)值乘以權(quán)系數(shù)γi(i=1,2,3),將式(2)中的目標(biāo)函數(shù)改寫(xiě)為如下形式,則多目標(biāo)優(yōu)化問(wèn)題轉(zhuǎn)化為一維的單目標(biāo)優(yōu)化問(wèn)題[12]。
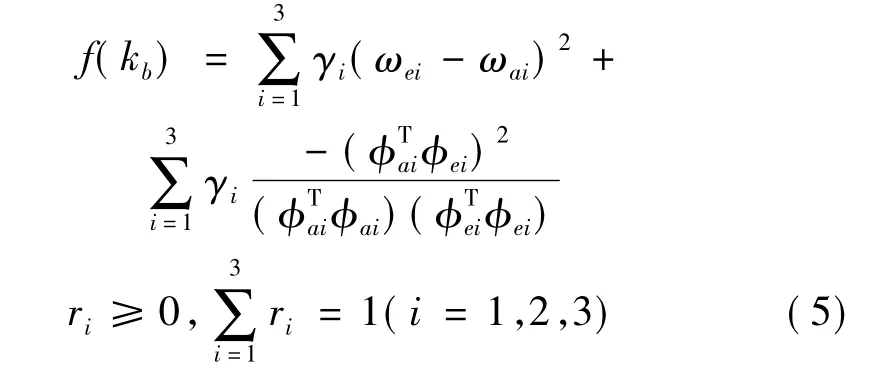
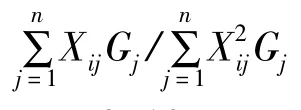
該優(yōu)化問(wèn)題采用經(jīng)典0.618法求解最優(yōu)的kb值。
本文討論的結(jié)構(gòu)隔震層在多遇地震設(shè)計(jì)水平等效剛度為40 800 kN/m,結(jié)合前面的假定,迭代初始區(qū)間[kb1,kb2]取為[0.3,0.5]×106kN/m,收斂容差 ε 取0.01。
經(jīng)迭代計(jì)算,得出在環(huán)境激勵(lì)下隔震層的實(shí)際水平等效剛度kb=444 720 kN/m,其值為多遇地震設(shè)計(jì)時(shí)所取水平等效剛度的10.9倍,另外該值也大于結(jié)構(gòu)第三層和第四層的層間剪切剛度值。
環(huán)境激勵(lì)下及不同隔震支座剪切變形時(shí)基礎(chǔ)隔震結(jié)構(gòu)的動(dòng)力特性對(duì)比見(jiàn)表5。

表5 隔震結(jié)構(gòu)動(dòng)力參數(shù)隨隔震支座不同剪切變形的變化Tab.5 Dynamic parameters of base-isolated structure with different shear deformation of rubber bearings
表5表明,不同振動(dòng)幅值時(shí)隔震層的等效水平剛度和等效黏滯阻尼比相差較大,結(jié)構(gòu)體系的基本周期相應(yīng)地也有較大變化。
值得注意的是該建筑設(shè)計(jì)計(jì)算階段所得的隔震前基本周期為0.460 4 s,大于在環(huán)境激勵(lì)下實(shí)測(cè)的隔震后周期值0.334 4 s,這固然與隔震層在環(huán)境激勵(lì)下剛度較大有關(guān)系,另外理論建模與實(shí)際施工之間的差異以及理論建模是否能考慮影響結(jié)構(gòu)動(dòng)力特性的所有主要因素也是值得進(jìn)一步研究的。
隔震層在微幅振動(dòng)激勵(lì)下的水平等效剛度很大,從結(jié)構(gòu)抗風(fēng)角度來(lái)講是合理的,可以保證隔震建筑在風(fēng)振激勵(lì)下的舒適性能。
5 基于反演隔震層水平剛度的有限元模型修正
將反演所得的隔震層等效水平剛度反饋到初始有限元模型,得到修正后的有限元模型。依據(jù)修正后的有限元模型分析所得的前三階振型的頻率及其與試驗(yàn)識(shí)別結(jié)果及初始有限元分析結(jié)果的對(duì)比如表6所示。修正后的前三階振型如圖7所示。
表6結(jié)果及圖5和圖7的對(duì)比表明,修正后的有限元模型分析所得的頻率與試驗(yàn)識(shí)別得到的頻率吻合較好,兩者的振型形狀也基本相似,前三階的MAC值都在0.88以上,表明計(jì)算振型與實(shí)測(cè)振型之間有較好的相關(guān)性[13]。

表6 修正前后前三階模態(tài)頻率與識(shí)別頻率的對(duì)比及修正后分析模態(tài)與識(shí)別模態(tài)的MACTab.6 Comparison of first 3 frequencies from ambient vibration test,initial model,updated model and MACs between updated modes and identified modes

圖7 修正后有限元模型分析所得的前三階振型Fig.7 First 3 mode shapes from updated finite element model
6 結(jié)論
對(duì)兩棟基礎(chǔ)隔震建筑在環(huán)境激勵(lì)下的動(dòng)力測(cè)試及模態(tài)參數(shù)的識(shí)別結(jié)果表明,環(huán)境激勵(lì)下基礎(chǔ)隔震結(jié)構(gòu)的動(dòng)力性能與設(shè)計(jì)分析階段所考慮的動(dòng)力性能差別很大,結(jié)構(gòu)的基本周期和模態(tài)阻尼比均遠(yuǎn)小于多遇地震和罕遇地震設(shè)計(jì)工況下的相應(yīng)值。因此,為了進(jìn)一步研究基礎(chǔ)隔震結(jié)構(gòu)在環(huán)境激勵(lì)下的動(dòng)力性能,選擇其中一棟為研究對(duì)象,利用多目標(biāo)優(yōu)化的方法反演分析了隔震層在環(huán)境激勵(lì)下的實(shí)際水平等效剛度,反演所得的隔震層水平等效剛度為多遇地震工況下計(jì)算剛度取值的10.9倍。最后基于反演的實(shí)際隔震層水平等效剛度對(duì)結(jié)構(gòu)的初始有限元模型進(jìn)行了修正,修正后模型的數(shù)值分析結(jié)果與實(shí)際測(cè)試結(jié)果的對(duì)比表明,修正后的模型可以更好地反映結(jié)構(gòu)在環(huán)境激勵(lì)下的動(dòng)力特性。
另外,測(cè)試分析結(jié)果也表明,識(shí)別所得的隔震結(jié)構(gòu)前三階振型的阻尼比都相對(duì)較小,基礎(chǔ)隔震結(jié)構(gòu)的等效黏滯阻尼比的大小近乎于未隔震結(jié)構(gòu)的阻尼比,因此,隔震層對(duì)整體結(jié)構(gòu)的阻尼貢獻(xiàn)較小,在環(huán)境激勵(lì)等微幅振動(dòng)影響下,基礎(chǔ)隔震結(jié)構(gòu)可以視為經(jīng)典的比例阻尼系統(tǒng)。
[1]莫 庸,金建民,杜永峰,等.高烈度地震區(qū)建筑結(jié)構(gòu)選型問(wèn)題的初步探討——5.12汶川大地震隴南地區(qū)建筑結(jié)構(gòu)震害考察中結(jié)構(gòu)選型問(wèn)題的思考[J].工程抗震與加固改造,2008,30(4):50-55.
[2]GB50011-2010.建筑抗震設(shè)計(jì)規(guī)范[S].北京:中國(guó)建筑工業(yè)出版社,2010.
[3]Skinner R I,Robinson W H,Mcverry G H.工程隔震概論[M].謝禮立,周雍年,趙興權(quán),譯.北京:地震出版社,1996.
[4] Ventura C E,F(xiàn)inn W D L,Lord J F,et al.Dynamic characteristics of a base isolated building from ambient vibration measurements and low level earthquake shaking[J].Soil Dynamics and Earthquake Engineering,2003,23(4):313-322.
[5]Han J P,Lu X L,Wang F X.Comparison of modal parameter identification algorithms based on shaking table model test data[C]//The International Society for Optical Engineering,2009:73750K-1-7.
[6]Overschee P V,Moor B D.Subspace identification for linear systems: theory, implementation, applications[M].Dordrecht:Kluwer Academic Publishers,1996.
[7] Juang J N.Applied system identification[M].Englewood Cliffs:Prentice-Hall Inc,1994.
[8] Allemang R J,Brown D L.A correlation coefficient for modal vector analysis[C].Proceedings of the First International Modal Analysis Conference (IMAC), Orlando,F(xiàn)lorida;1982.
[9]杜永峰,李 慧,Spencer B F,等.非比例阻尼隔震結(jié)構(gòu)地震響應(yīng)的實(shí)振型分解法[J].工程力學(xué),2003,20(4):24-32.
[10] Pines D,Salvino L.Structural health monitoring using empirical mode decomposition and the Hilbert phase[J].Journal of Sound and Vibration,2006,294(1-2):97-124.
[11] Ceravolo R.Use of instantaneous estimators for the evaluation of structural damping[J].Journal of Sound and Vibration,2004:385-401.
[12]明圖章,胡光偉,黃 衛(wèi).大跨徑鋼橋面鋪裝體系多目標(biāo)優(yōu)化設(shè)計(jì)[J].土木工程學(xué)報(bào),2007,40(2):70-73.
[13]任偉新,彭雪林.青洲斜拉橋的基準(zhǔn)動(dòng)力有限元模型[J].計(jì)算力學(xué)學(xué)報(bào),2007,24(5):609-613.

