地下結構靜－動力分析中的人工邊界轉換方法研究

高 峰，趙馮兵

（重慶交通大學 土木建筑學院，重慶 400074）

人工邊界從廣義上可分為靜力人工邊界和動力人工邊界。靜力人工邊界由來已久，通常有固定邊界、滾軸邊界等。動力人工邊界經過幾十年的發展，已形成全局人工邊界和局部人工邊界兩大類別，并應用于各自適應的工程計算中［1］。此外，王后裕、陳上明等［2］將透射邊界應用于考慮結構與圍巖動力相互作用的地下離壁式框架結構地震分析模型，陳萬祥、郭志昆等［3］將粘彈性支承應用于低速沖擊下的邊界梁反應，均取得了較好的效果。

動力人工邊界發展到現在已有透射邊界、粘性邊界、粘彈性邊界等幾種類型。Deeks［4］提出粘彈性人工邊界。劉晶波等人［5，6］發展了二維的粘彈性人工邊界，以后將其發展為三維時域粘彈性人工邊界。盧華喜等人［7］考慮土的動力非線性性質，基于土體等效線性模型中的動模量變化模式，推導了適用于土－結構動力相互作用的粘彈性人工邊界。劉晶波等人［8，9］將二維粘彈性邊界發展成一致粘彈性人工邊界及其對應的粘彈性邊界單元，后來又推導了三維一致粘彈性人工邊界及等效粘彈性邊界單元。

地下結構動力響應分析中一般需要考慮初始應力場，可稱之為靜－動力分析問題，其一般算法為先對模型進行靜力分析，求出靜應力場，然后以此為初始條件進行動力分析。目前對線彈性小變形范圍內的靜－動力分析問題，普遍做法是采用靜力人工邊界和動力人工邊界分別對靜力和動力問題進行計算，將計算結果進行疊加得到完整的結果［1］。

對于涉及非線性或大變形問題的靜－動力分析，靜力分析轉換到動力分析時人工邊界常用處理方法主要有以下幾種：① 靜力分析中采用滾軸邊界或固定邊界，動力分析采用粘彈性邊界、透射邊界、粘性邊界等人工邊界；② 靜力分析和動力分析都采用靜－動力統一邊界，如粘彈性靜－動力統一人工邊界；③ 靜力分析和動力分析都采用滾軸邊界或固定邊界。

對第③種方法，由于固定邊界使波動全部反射，已有許多文獻證明其具有放大振動效應的作用，目前已經使用得不多。劉晶波等人基于粘彈性動力人工邊界和半無限空間中靜力問題的基本解，建立了對動力問題和靜力問題均適用的三維粘彈性靜－動力統一人工邊界，從而上述第②種方法得以解決［1］。

然而，在使用人工邊界對地下結構進行動力分析時，還存在一些問題。如第（1）種方法，由于對靜－動力分析中的人工邊界轉換原理認識不清，將使計算結果嚴重偏離預期值，失去了施加動力人工邊界的必要性。在第②種方法中，將粘彈性靜－動力統一人工邊界應用于地下結構的靜力分析時，其計算結果誤差較大。本文將就此兩個問題進行論證和分析，并闡述合理的地下結構靜－動力分析人工邊界轉換方法。

1 靜力和動力有限元分析原理

1.1 靜力分析原理

地鐵等地下工程中初始應力場的確定須先計算未開挖狀態下圍巖的自重應力場，進而根據施工步驟，采用釋放荷載法，計算出襯砌結構和圍巖的靜應力場［10］。許多地下結構的自重應力場模型可以假設為半無限空間體，根據經典圍巖壓力理論和彈性力學理論，半無限空間體中距地表面任一深度h處的應力狀態可定義為［11，12］：

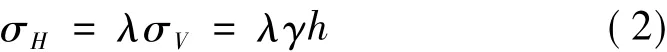
式中，σV為豎向應力，γ為圍巖重度，σH為橫向應力，λ為側壓力系數。對淺層圍巖，可假設其為各向同性介質，側壓力系數可表示如下［11］：

對有限元計算中所取的有限區域，可以據此確定有限域邊界條件。

1.2 靜力分析邊界條件

根據上述靜力分析方法，在靜、動力共同作用問題的計算中，在進行動力分析之前須先確定地下結構模型的靜應力場。地下結構開挖前可將大地假設為半無限空間體，其在重力作用下的靜力計算，根據對稱性，模型中任一處的水平位移uH=0。因此，計算該應力場時，有限區域模型兩側可用水平約束即法向約束，底部可用全約束或僅約束豎直方向，頂面即地面應為自由邊界。

1.3 動力分析原理

在動力荷載作用下，有限元體系在t+Δt時刻的運動平衡方程為：

式中α、β為常數，可按兩種不同的振動頻率下測得的阻尼比ξ加以確定。

1.4 粘彈性人工邊界

粘彈性人工邊界從用途上可分為動力人工邊界和靜－動力統一人工邊界；從具體實現方法上可分為彈簧－阻尼器邊界單元和一致粘彈性邊界單元。

實際應用中模型邊界單元的物理力學參數由其相鄰的圍巖介質材料決定，具體計算公式參考相關文獻［1，5－9］。結合有限元法具體實現時，此處采用一致邊界，即在人工邊界處設置一層與主計算區域單元有著相同形函數的單元，其等效剪切模量、等效彈性模量和等效阻尼系數表達形式如下：

其中等效阻尼系數取的是法向和切向的平均值。式中h為等效邊界單元厚度，為等效泊松比，E、G、μ和ρ分別為介質彈性模量、剪切模量、泊松比和質量密度。R為波源至人工邊界點的距離；cs和cp分別為S波和P波波速；αT與αN分別為切向與法向粘彈性人工邊界參數，具體取值情況見表1。等效泊松比可按如下取值

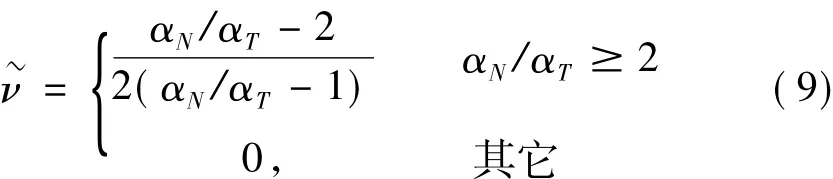
表1 粘彈性動力人工邊界中參數α的取值Tab.1 The values of α in viscous-spring artificial boundary for dynamic analysis

表2 粘彈性靜－動力統一人工邊界中參數α的取值Tab.2 The values of α in unified viscous-spring artificial boundary for static and dynamic analysis

靜－動力統一人工邊界是在上述動力人工邊界的基礎上對人工邊界參數α進行調整，其具體取值見表2。其中參數α*具體計算公式：

式中μ為圍巖泊松比，R為荷載作用點到人工邊界點的距離，d為位置坐標。對于底面人工邊界，式中d取荷載作用點至邊界單元的水平距離；對于側面人工邊界，式中d取荷載作用點至邊界單元的垂直距離。

2 兩種地下結構靜－動力人工邊界轉換方法邊界轉換原理分析

動力計算的初始時刻，未施加動力荷載前，整個模型各點加速度均為零。地下結構靜－動力分析中，要求動力分析以靜力分析結果為初始條件，則模型在動力計算初始時刻處于靜力平衡狀態。因此人工邊界的轉換可從靜力學方面討論。

在引言中已經介紹了地下結構靜－動力分析中人工邊界的常用三種處理方法，下面對第①和第②種方法的人工邊界轉換原理進行分析。

第①種人工邊界轉換方法（方法①）：

該方法靜力分析中采用滾軸邊界或固定邊界（可稱之為傳統靜力邊界條件），動力分析中采用粘彈性動力人工邊界。一般計算過程如表3所示，具體為：先采用靜力計算方法按釋放荷載法計算地下結構的開挖過程得到初始靜應力場等結果；然后以此靜力計算結果為初始條件進行動力計算。

表3 方法①靜動力邊界條件和荷載條件表Tab.3 Boundaries and loads of the static analysis and the dynamic analysis in method①

下面討論動力計算初始條件中所應輸入的靜力計算結果。

靜力計算中總體剛度平衡方程可表為：

式中［K］為剛度矩陣；{F}為等效節點力向量；{FA}為靜力計算中所施加的全部外荷載引起的等效節點力；{FR}為全部約束反力向量，須經此方程引進邊界條件求出{u}后，才能求得。

靜力計算中可同時算得模型靜應力場：

式中［D］、［B］和{u}e分別為彈性矩陣、幾何矩陣和單元節點位移向量。

從此應力場的求解過程可以看出，當以此應力場為初始條件進行新的計算時，對模型施加引起此應力場的荷載和約束是模型保持平衡的必要條件。

由于邊界節點在約束或指定位移方向不會對邊界以內節點產生等效節點力，（11）式可以表示成：

其中：c表示邊界以內自由度，b表示邊界自由度，A表示與施加的外荷載相關，R表示與反力相關。該式經引入邊界條件可得縮減的剛度平衡方程：

由式（14）和式（15）可以解得約束反力引起的節點荷載向量即約束反力向量為：

去掉約束條件后，將式（16）所示的約束反力代入式（14），仍可解得{ub}為零，且{uc}的解也不變。

這說明對模型施加約束條件與在邊界施加相應的約束反力在靜力計算中是等效的，這使得靜－動力分析中以靜力計算結果為初始條件時，可以將約束條件去掉施加以相應的約束反力，而不改變模型的靜力平衡狀態。

綜上可得，在地下結構靜－動力分析中，以靜力分析結果中的應力場為初始條件進行動力分析時，為保證模型在動力計算初始時刻為靜力平衡狀態，可在輸入靜應力場的同時輸入引起此應力場的荷載和約束；轉換邊界時，須去掉約束條件，只要同時施加以相應的約束反力即可。

方法①在應用中經常因為未將動力計算初始條件完整輸入模型而導致不合理的結果，未輸入靜力計算約束反力就是典型的一種。圖1就是在這種計算條件下對某地下結構彈性模型在兩種荷載條件下進行靜－動力分析所得的模型中某一點的動力反應。圖中振動荷載是指如圖8所示的列車振動荷載，零動力荷載是指動力分析中所施加的振動荷載（或動力荷載）為零。

從圖1（a）和圖1（b）可以看出，該點的位移和應力均呈現首先大幅波動，然后逐漸趨于穩定的情形。從圖1（c）和圖1（d）可以看出，該點的位移和應力在沒有任何動力荷載情況下仍出現類似波動情形。

圖1 某地下結構模型動力響應Fig.1 Dynamic response in a underground structure modal

模型在任何動荷載情況下仍產生較大位移和應力，說明模型在零時刻就受到一個或一組不平衡力。由此可知模型靜－動力轉換后未施加靜力分析約束反力將導致不合理的結果，亦可得此方法中完整施加動力計算初始條件的必要性。

表4 方法②靜動力邊界條件和荷載條件表Tab.4 Boundaries and loads of the static analysis and the dynamic analysis in method②

第②種人工邊界轉換方法（方法②）：

該方法在靜力計算與動力計算中均采用粘彈性靜－動力統一人工邊界。計算過程與方法①類似，仍先采用靜力計算方法按釋放荷載法計算隧道的開挖過程得到隧道靜應力場；然后以此靜應力場為初始條件進行動力計算。靜力分析和動力分析中的荷載和邊界條件如表4所示。

由上述對方法①的分析可知，方法②在計算過程中邊界條件并未改變，只須按方法①中輸入初始應力場的方法輸入初始條件即可。

由此可知，方法②的計算過程在理論是合理的，但其人工邊界的在具體工程實例中的靜力計算精度有待檢驗。

3 粘彈性靜－動力統一人工邊界的靜力分析精度

上述第②種方法從靜力分析轉換到動力分析時靜應力場和荷載等的過渡是合理的，下面檢驗其相應人工邊界的靜力計算精度。

由于半無限空間體具有經典彈性力學解，即使在巖土力學中也有理論解，前面已有論述；因此，對半無限空間體的有限元模型進行靜力分析，將結果與理論解進行對比，可以檢驗其計算方法的有效性。該模型的理論解可以通過式（1）、式（2）和式（3）算得。

表5 三種工況靜力計算條件表Tab.5 Static calculation conditions of three conditions

圖2 半無限空間體理論解模型（工況一）Fig.2 Half space modal of the theoretical solution（Condition 1）

圖3 傳統靜力邊界模型（工況二）Fig.3 Static modal of the traditional boundaries（Condition 2）

圖4 粘彈性靜－動力統一人工邊界模型（工況三）Fig.4 Static modal of the unified viscous-spring boundary for static and dynamic analysis（Condition 3）

為了比較，進行了三種工況的計算，具體的計算步驟和計算條件見表 5。其中工況一為理論解，圍巖性質同表6，其計算模型分別如圖2、圖3和圖4所示。工況三人工邊界彈性模量的計算采用了動力荷載施加點處于模型幾何中心點的假設。

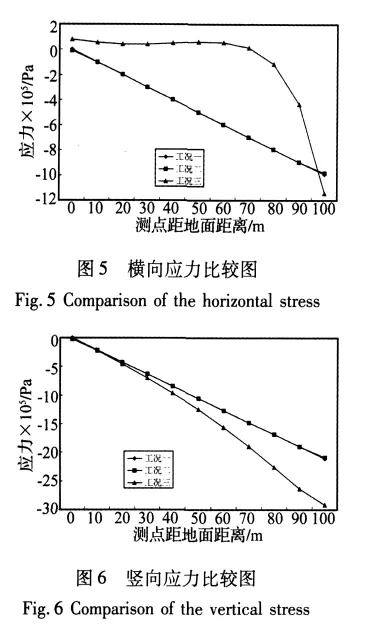
在模型對稱軸上設置觀測點，由地面向下每10m設置一個觀測點，并將三種工況計算結果繪于同一圖中進行比較，比較結果見圖5和圖6。

從圖中可以看出，該有限元模型在施加粘彈性靜－動力統一人工邊界時，其靜力計算結果與理論解相比有較大誤差，特別是橫向應力結果誤差較大；而其施加前面所述傳統靜力邊界條件時，豎向應力和橫向應力結果都幾乎與理論解重合。

這說明粘彈性靜－動力統一人工邊界應用于受重力作用的半無限空間體的有限元模型靜力計算時，其誤差偏大。而傳統的靜力邊界即滾軸邊界或固定邊界應用于該有限元模型時精度較好。

4 推薦的地下結構靜－動力分析人工邊界轉換方法

方法（2）在靜－動力分析時采取了統一的人工邊界，應用比較方便，但其相應人工邊界靜力分析誤差偏大，從而造成動力分析結果不合理。

由上述對方法（1）的分析得出，較為合理的地下結構的靜－動力分析可采用如下計算步驟：

（1）采用靜力約束條件對模型進行靜力分析，計算結果應包括應力場和約束反力。

（2）將靜力模型中的約束條件去掉，施加粘彈性人工邊界。

（3）在原靜力約束被去掉的地方施加約束反力，對模型施加靜力場和靜力荷載（如重力加速度或其他恒力）。

（4）對模型施加動力荷載，進行動力計算。

模型在動力計算初始時刻處于靜力平衡狀態，這是檢驗邊界轉換合理與否的標準。具體實現時可在動力計算中施加零動力荷載，并查看模型應力位移等的時程反應。

表6 圍巖物理力學參數表Tab.6 physical and mechanical parameters of the rock

某雙線鐵路隧道，其凈空跨度 10.2m，為三心圓斷面；襯砌初期支護15cm，二次襯砌30cm；隧道埋深 45m，Ⅳ類圍巖。采用ANSYS大型有限元分析軟件對該隧道進行建模和計算，模型區域豎向取100m，橫向取100m。隧道及圍巖物理力學參數見表6。

圖7 推薦的方法動力分析模型Fig.7 Modal of tunnel for the dynamic analysis in the recommended method

對該隧道進行列車荷載作用下的振動分析。該算例中的動力計算模型可表示為圖7所示模型，其中FR為靜力分析的約束反力，P（t）為動力荷載。

圖8 振動荷載時程曲線Fig.8 Time history curve of the vibration load

計算分為在動力分析中施加振動荷載（圖8所示）和零動力荷載兩種情況。

圖9（a）和圖9（b）是施加振動荷載情況下拱頂的豎向位移和第一主應力時程曲線。圖9（c）和圖9（d）是施加零動力荷載情況下拱頂的豎向位移和第一主應力時程曲線圖。

從圖9（a）和9（b）可以看到，拱頂的豎向位移和第一主應力均呈現初期波動較大，然后逐漸演變為穩態振動；豎向位移最大振幅約0.045mm，第一主應力最大振幅約140Pa。而圖9（c）和圖9（d）顯示在零動力荷載作用下，隧道拱頂發生極小的振動，豎向位移最大振幅約1.4×10－6mm，第一主應力無振動，此可視為數值計算誤差，可以忽略不計。據此可以推斷動力分析初始時刻模型處于很好的平衡狀態，從而說明其人工邊界轉換更為合理。

圖9 拱頂動力響應Fig.9 Calculated dynamic response at the vault crown

5 結論

本文通過將粘彈性人工邊界應用于同時考慮靜力效應和動力效應的地下結構靜－動力分析，推薦了一種較為合理的地下結構靜－動力分析的人工邊界轉換方法，并得到以下結論：

（1）靜－動力分析人工邊界轉換時須保證模型動力分析在零時刻為靜力平衡體；靜－動力人工邊界轉換方法準確性，可以通過在動力分析中施加零動力荷載來進行檢驗。

（2）在分析過程中均采用粘彈性靜－動力統一人工邊界時，該靜－動力分析從靜力狀態到動力分析的過渡是合理的。但該邊界在半無限體有限元模型的靜力計算中誤差較大，因此，該人工邊界在地下結構靜－動力分析中應謹慎使用。

［1］劉晶波，李 彬.三維黏彈性靜－動力統一人工邊界［J］.中國科學（E輯），2005，35（9）：966－980

［2］王后裕，陳上明，言志信，等.考慮動力相互作用的地下平面鋼框架地震反應分析［J］.振動與沖擊，2005，24（1）：99－103.

［3］陳萬祥，郭志昆.粘彈性邊界梁在低速沖擊下的動力響應分析［J］.振動與沖擊，2008，27（12）：69－72，78，108.

［4］ Deeks A J.Randolph M F.Axisymmetric time-domain transmitting boundaries［J］. Journal of Engineering Mechanics，1994，120（1）：25 － 42.

［5］劉晶波，呂彥東.結構－地基動力相互作用問題分析的一種直接方法［J］.土木工程學報，1998，31（3）：55－64.

［6］劉晶波，王振宇，杜修力，等.波動問題中的三維時域粘彈性人工邊界［J］.工程力學，2005，22（6）：46－51.

［7］盧華喜，梁平英，尚守平.地基非線性波動問題中黏－彈性人工邊界研究［J］.巖土力學，2005，29（7）：1911－1916.

［8］劉晶波，谷 音，杜義欣.一致粘彈性人工邊界及粘彈性邊界單元［J］.巖土工程學報，2006，28（9）：1070－1075.

［9］谷 音，劉晶波，杜義欣.三維一致粘彈性人工邊界及等效粘彈性邊界單元［J］.工程力學，2007，24（12）：31－37.

［10］高 峰，關寶樹.深圳地鐵地震反應分析［J］.西南交通大學學報，2001，36（4）：355－359.

［11］關寶樹.隧道力學概論［M］.成都：西南交通大學出版社，1993.

［12］徐芝綸.彈性力學（上冊）［M］.北京：高等教育出版社，2006.

［13］潘昌實.隧道力學數值方法［M］.北京：中國鐵道出版社，1995.