基于工作應變模態損傷識別方法的試驗研究

顧培英，鄧 昌，湯 雷

（1.南京水利科學研究院，南京 210029；2.水利部水科學與水工程重點實驗室，南京 210029）

結構損傷診斷首先需解決損傷標識量的選擇問題，李德葆等［1］研究得到了六種損傷識別指標的靈敏度，應變型指標比位移型指標對損傷具有更好的識別能力。筆者也進行了相關試驗研究和數值仿真分析，得出簡支梁和渡槽結構應變模態損傷規律及其損傷識別優勢［2～5］。但目前所涉及的損傷指標法大多數是基于位移類模態（或參數）。

損傷狀態下的模態數據需通過模態試驗獲得，而傳統的模態試驗需對結構進行人工激勵，但此方法無法實現在線試驗，且許多結構人工激勵又較為困難，所以，人們提出了基于環境激勵的位移模態試驗方法。該方法已在航天、航空、汽車、建筑及橋梁領域成功應用，但本文討論的是基于環境激勵的應變模態問題。這里定義環境激勵下的應變模態為工作應變模態OSMS（Operational strain mode shape）。目前，筆者已建立了基于環境激勵下的工作應變模態識別法［6，7］，并開展了應變模態數值仿真分析［3］、人工激勵下的應變模態模型試驗［2，4］。

現有損傷指標法是結合有限元模型分析，根據實測模態數據，利用結構損傷前后動態參數變化構造合適的損傷指標，判別損傷的存在、位置或程度。常用的損傷識別指標主要有兩類［8～10］：①相關弱化型，以損傷前后相關系數弱化為損傷識別指標；②極差型，以損傷前后模態參數差為損傷識別指標。但在實際結構損傷評估中，要得到損傷前的精確狀態非常困難。為此，筆者近幾年提出了基于損傷應變模態差分（Strain Mode Shape Difference）原理的損傷位置直接指標法ISMSD、基于局域應變模態面積（Local Strain Mode Shape Area）的損傷程度直接指標法ILSMSA，兩指標無需利用損傷前的模態數據［8，11］。

本文在簡要介紹以上方法的基礎上，針對環境激勵下的應變模態進行模型試驗研究，驗證所提出的工作應變模態識別方法；并結合數值仿真分析，驗證并完善了所提出的損傷識別方法。

1 工作應變模態頻域識別方法

文獻［6］中推導得到具有粘性阻尼n自由度系統的應變頻響函數矩陣Hε（ω）為：

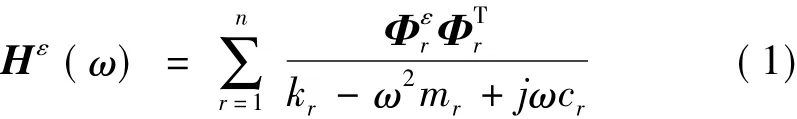
式中：Hε（ω）為應變頻響函數矩陣；Φr為第r階位移模態矢量；為第r階應變模態矢量；kr、mr、cr分別為第r階模態剛度、模態質量、模態粘性比例阻尼系數。

根據式（1）可知，應變頻響函數矩陣任一列包含了應變模態的所有信息，因此環境激勵位移模態試驗頻域法完全可應用到應變模態中來。

2 損傷識別直接指標法

2.1 損傷位置直接指標法

梁式結構研究結果表明，損傷影響區范圍可近似地由損傷點為中心的三段直線組成［11］。j點損傷位置直接指標值可表示為［11］：

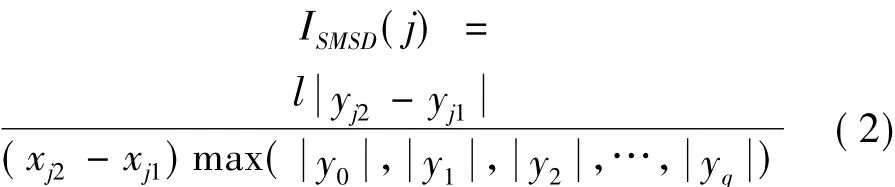
式中：ISMSD（j）為某階應變模態差分曲線第j個有效零值點損傷位置直接指標值；l為梁式結構跨度；xj1、xj2為對應于有效零值點j的有效極值點x值；yj1、yj2為對應于有效零值點j的有效極值；y0、y1…yq為所有有效極值；q為有效極值點個數。

ISMSD（j）值越大，j點處損傷可能性越大。再結合差分曲線變化規律，即可判斷損傷位置。

2.2 損傷程度直接指標法

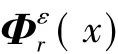
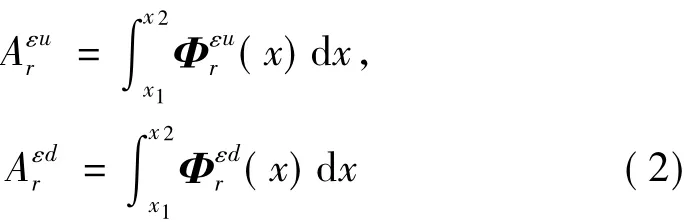
令r階應變模態損傷面積為Δ，則：

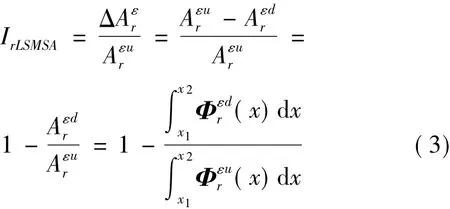
式中：IrLSMSA為第r階局域應變模態面積損傷程度直接指標。

3 模型試驗

模型采用工字鋼懸臂梁，圖1為模型截面圖。該模型梁長3.00 m，分別在距自由端2.60 m和2.90 m處采用螺栓固定。模型劃分成30等份，共31個測點，在各測點（位于上腹板）粘貼電阻應變計。首先對完好懸臂梁進行錘擊激勵下的應變模態、環境激勵下應變模態（即工作應變模態）試驗，再分別在 1.80 m、1.00 m上翼緣處切割1 mm寬的裂縫，裂縫深度為整個翼緣厚度。共開展6組工況的應變模態試驗。

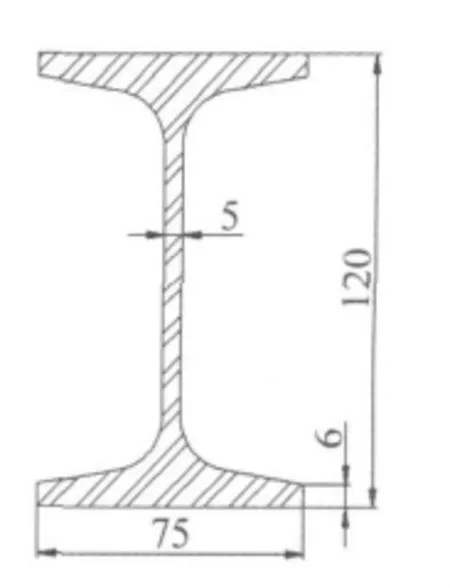
圖1 模型截面圖（單位：mm）Fig.1 Section of model（unit：mm）

3.1 工作應變模態

通過第1節介紹的應變模態識別方法識別出前二階工作應變模態，圖2為工作應變模態與錘擊激勵下的應變模態比較，其中1損傷表示在1.80 m處存在損傷，2損傷表示分別在1.80 m、1.00 m處存在損傷。

根據圖2可知，利用筆者提出的方法識別出的工作應變模態與錘擊激勵下的應變模態形狀相似，除支座和節點附近外，各工況下的振型相對值平均相差6%。所以，該方法可較好地識別工作應變模態。此外，第1階應變模態在1.80 m、1.00 m損傷處變化較為明顯，第2階應變模態在1.00 m損傷處變化較為明顯。

3.2 損傷位置直接指標

圖3為工作應變模態差分曲線，由圖3可知，完好狀態下的工作應變模態差分曲線除固定支座附近外，變化較為平緩。損傷狀態下的工作應變模態差分曲線在損傷處發生劇烈變化，從極大（或極小）值經過損傷點很快達到另一極小（或極大）值。兩極值點之間幾乎呈直線關系，極值點外一定影響范圍內的差分曲線也幾乎呈直線，一定范圍之外，該直線逐漸過渡到另一較為平坦的曲線或直線。兩過渡點間的范圍即為損傷影響區，簡而言之，損傷影響區范圍可近似地以損傷點為中心的三段直線組成，該結構平均損傷影響區范圍為0.49m。對于多損傷結構，只要損傷間距大于影響區范圍，損傷位置即可按單損傷方法判定。

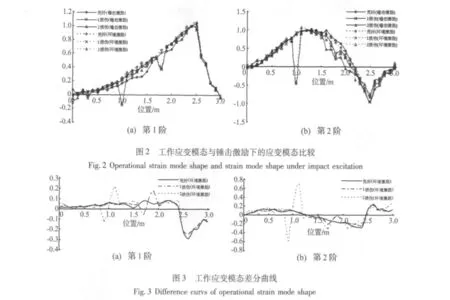
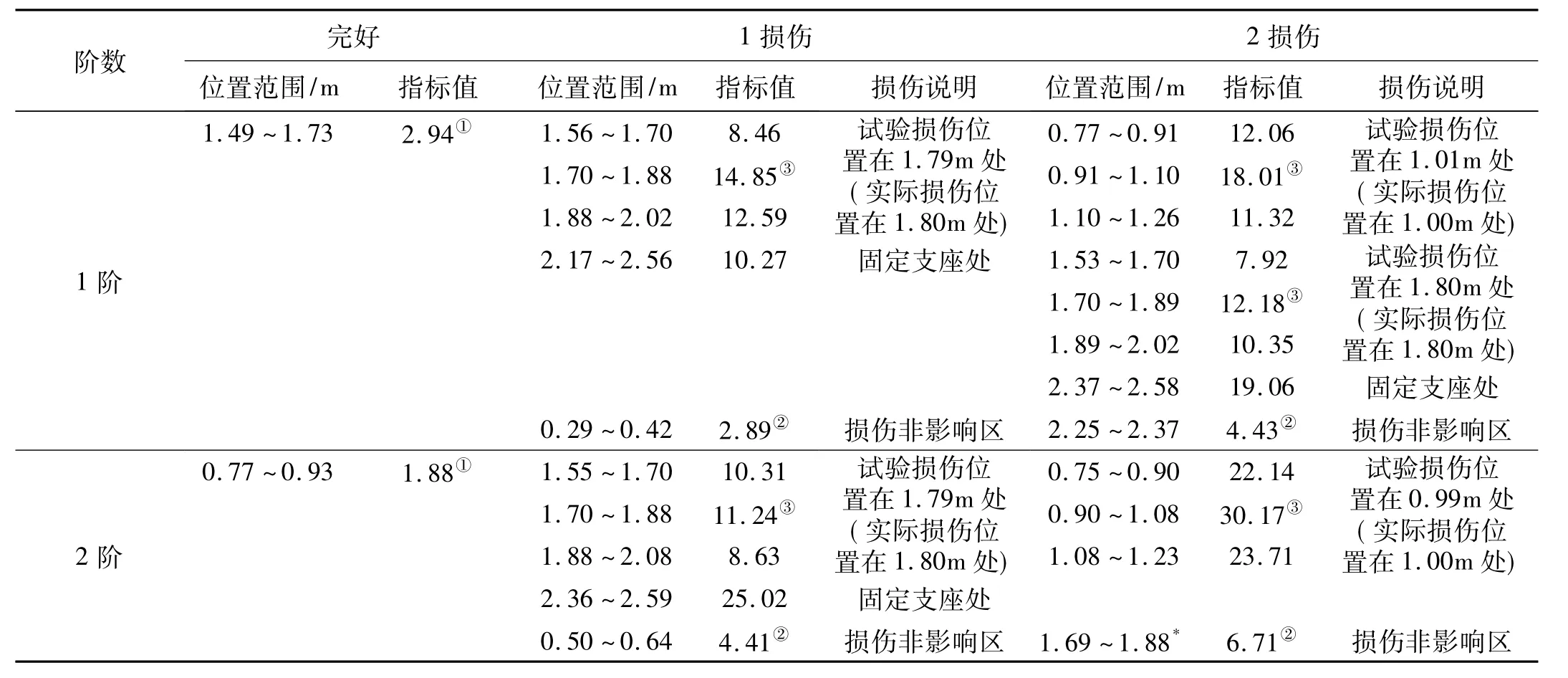
表1 損傷定位指標計算結果Tab.1 Direct index of damage location detection

需要說明的是，根據文獻［8］中簡支梁數值仿真研究結果，將應變模態差分曲線兩極值點間的零點處確定為損傷點。而根據本文懸臂梁損傷狀態下模型試驗結果，選擇兩極值點間的中點所對應的位置為損傷點更為合理。該點與零值點位置略有差異，這是由于試驗測點不可能非常密集，試驗極值點、零值點與理論值會有偏差所致。損傷定位指標計算結果如表1所列。

根據表1可知，除固定支座附近外，完好狀態下前2階最大指標值分別為2.94、1.88；損傷處的指標值在11.24～30.17；損傷非影響區最大指標值在 2.89 ～6.71。損傷處指標值平均是損傷非影響區的4.1倍，遠大于非損傷處指標值，且識別出的損傷位置與實際位置一致。所以，根據指標值及應變模態差分曲線分布規律可進行損傷定位。

3.3 損傷程度直接指標

根據圖2中的工作應變模態可以發現，在損傷處應變模態值變化劇烈，該處應變模態值明顯減小，甚至反向，對損傷狀態下出現反向的工作應變模態，如果仍按2.3節損傷程度直接指標法計算，則損傷程度直接指標值會偏大，為此需對該指標法進行改進。在損傷曲線的損傷處作一條水平線，將影響區擬合曲線、影響區左右邊界與該水平線所圍面積定義為應變模態完好面積；應變模態損傷面積、局域應變模態面積損傷程度指標定義不變。

利用改進后的損傷程度指標法，計算試驗工作應變模態損傷程度指標，為了較為全面分析該指標，還對相應數值仿真損傷應變模態曲線進行了計算分析，其中損傷位置、損傷量與模型試驗相同。損傷程度指標如表2所列。

表2表明，同一損傷量下的損傷程度指標變化不大，與損傷位置、模態階數、是否歸一化無關；多損傷規律與單損傷相似；試驗損傷程度指標值大于數值仿真指標值23%。這主要是由于試驗時，測點不可能非常密集，應變模態曲線的漸變性不可能完全反映出來，試驗曲線的突變性更為明顯，相應的損傷影響區偏小，因而完好面積偏小，損失程度指標也就偏大。

表2 損傷程度指標Tab.2 Direct index of damage degree detection

實際應用時，損傷程度直接指標可根據測點布置的稀疏程度進行折減。對于測點按30等份布置的梁式結構，試驗結果偏大23%。一般情況下測點布置越稀，折減系數越大，具體折減規律還要開展進一步的試驗研究。

4 結論

（1）本文主要介紹了筆者近幾年提出的工作應變模態頻域識別方法、基于損傷應變模態差分原理的損傷位置直接指標法、基于局域應變模態面積的損傷程度直接指標法。應變頻響函數矩陣任一列包含了應變模態的所有信息，環境激勵位移模態試驗頻域法完全可以應用到應變模態中來。

（2）懸臂梁模型試驗及數值仿真計算分析結果表明，利用所提出的方法識別出的工作應變模態與錘擊激勵下的應變模態形狀相似，該方法能較好地識別工作應變模態。

（3）初步驗證并完善了損傷位置直接指標法、損傷程度直接指標法。

（4）懸臂梁損傷處損傷位置直接指標值平均是損傷非影響區的4.1倍，遠大于非損傷處指標值，且識別出的損傷位置與實際損傷位置一致，所以，根據指標值及應變模態差分曲線分布規律可進行損傷定位。同一損傷量下的損傷程度指標變化不大，與損傷位置、模態階數、是否歸一化無關；試驗損傷程度指標值大于數值仿真指標值23%。實際應用時可根據測點布置的稀疏程度進行折減。對于多損傷結構，只要損傷間距大于影響區范圍，損傷位置、損傷程度即可按單損傷方法確定。

需要指出的是，本文重點是從多損傷試驗的角度初步驗證所提方法，某些方面還需進一步完善，今后還要更多地開展不同損傷程度、不同測點間距的損傷直接指標比較研究。

［1］李德葆，陸秋海.實驗模態分析及其應用［M］.北京：科學出版社，2001，318 －322.

［2］顧培英，丁偉農.模態試驗在梁損傷診斷中的應用研究［J］.振動與沖擊，2004，23（3）：60－63.

［3］顧培英，陳厚群，李同春，等.應變模態技術診斷梁結構損傷［J］.地震工程與工程振動，2005，25（4）：50－53.

［4］顧培英，陳厚群，李同春，等.應用應變模態試驗技術診斷模型渡槽結構損傷［J］.河海大學學報，2006，34（4）：422－425.

［5］瞿偉廉，陳超，魏文輝.基于應變模態的鋼結構構件焊縫損傷定位方法的研究［J］.世界地震工程，2002，18（2）：1－8.

［6］顧培英，鄧 昌.基于環境激勵下的工作應變模態頻域識別方法［J］.振動與沖擊，2008，27（8）：68 －70.

［7］顧培英，鄧 昌，湯 雷.工作應變模態時域識別方法研究［J］.水力發電，2009，28（5）：27－29.

［8］顧培英，陳厚群，李同春，等.基于損傷應變模態的結構損傷識別直接指標法［J］.自然科學進展，2007，2：240－247.

［9］董 聰，范立礎，陳肇元.結構智能健康診斷的理論與方法［J］.中國鐵道科學，2002，23（1）：11－24.

［10］劉文峰，柳春圖.利用廣義應變比能進行結構損傷識別的數值研究［J］.機械強度，2003，2：159－162.

［11］顧培英，陳厚群，李同春，等.基于應變模態差分原理的直接定位損傷指標法［J］.振動與沖擊，2006，25（4）：13－17.