密肋復合墻-剪力墻混合結構水平位移計算方法研究
郭 猛,袁 泉,黃 煒,張旭鋒,李鵬飛
(1.北京交通大學 土木建筑工程學院,北京 100044;2.西安建筑科技大學 土木工程學院,西安 710055)
為了進一步提高在基本烈度為7度地震區建造密肋復合墻結構的層數和建筑總高度,解決基本烈度為8度地震區建造超過現有《密肋壁板結構技術規程》[1]中有關密肋結構總層數和總高度的限制問題,課題組近期提出了密肋復合墻-RC剪力墻混合結構[2-5](簡稱復合墻-剪力墻結構),如圖1所示。這種新型混合結構以密肋復合墻為主體,根據計算需要設置一定數量RC剪力墻,通過框架梁、連梁或樓板將密肋復合墻與混凝土墻聯合起來,共同抵御水平荷載作用,其中剪力墻可以是實體墻、帶縫墻、開洞墻等。由于混合結構的大部分抗側力構件為密肋復合墻,因而保持了密肋結構的諸多長處;同時由于加入部分剪力墻,增大了結構極限承載力和抗側剛度,減小了地震作用下樓層層間變形值,從而提高了密肋結構的整體抗震能力。剪力墻與復合墻變形機制的不同使得混合結構呈現雙重延性受力特點,即小震時剪力墻作為第一道防線起主要作用,中震和大震時剪力墻剛度出現退化,地震力由密肋復合墻與剪力墻按有效剛度分擔。作為試點工程,密肋復合墻-剪力墻混合結構體系已在寧夏銀川等地區的部隊營房建筑中得 到應用。
對于水平荷載下密肋復合墻-剪力墻結構位移的研究:文獻[6]建立了考慮復合墻彈性常數取值特點與剪切變形的密肋結構位移方程;文獻[2]從能量原理出發,通過推導結構體系的系統勢能方程和約束方程,構造輔助泛函并依據變分原理,得出混合結構的水平位移計算公式。基于能量的位移計算方法的主要缺點是需要多次試算構造出合理的輔助泛函,不同泛函形式決定了最終位移的不同計算精度。
本文簡要分析了復合墻-剪力墻混合結構的協同工作機制,依據密肋復合墻的彎剪型特點,采用經典的變形連續化協同工作方法,建立結構體系的位移微分方程,推導其水平位移的解析解,并通過算例分析混合結構的變形特點。
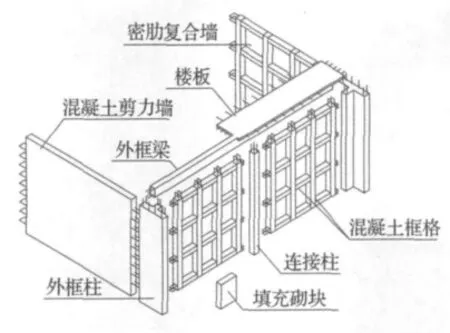
圖1 密肋復合墻-剪力墻混合結構Fig.1 Multi-grid composite wall-shear wall structure
1 復合墻-剪力墻結構協同工作機制
單獨承受水平荷載作用時密肋復合墻與剪力墻的變形特點不同:剪力墻以彎曲變形為主,中高層剪力墻一般忽略其剪切變形,隨著樓層的增加,總側移和層間側移增長較快;密肋復合墻的構造形式決定了墻體的主要彈性常數(Eeq、Geq)是與框格單元截面尺寸、框格布置方式等因素有關的變參數,且Eeq、Geq之間不存在線性的比例關系,變形大致屬于彎剪型,以彎曲變形為主還是以剪切變形為主取決于墻體抗彎剛度和抗剪剛度的相對大小。
復合墻-剪力墻混合結構中,框架梁、連梁或樓板把兩種墻肢聯系在一起,使得二者在各層樓板處協調變形。由于密肋復合墻存在剪切變形,但比框架結構要小得多,因此密肋復合墻-剪力墻結構的層間變形介于框架-剪力墻結構和剪力墻結構之間,小于框剪結構而大于剪力墻結構,與結構的剛度特征值有關。同時,由于復合墻單元的抗側剛度大于框架,以往由剪力墻擔負大部分外荷載的情況,變成由密肋復合墻與剪力墻共同承擔,連梁的協同作用相對于框架-剪力墻結構而言要小的多,這是與框架-剪力墻結構的重要區別之一。
彈性階段,復合墻與剪力墻協同工作時各自承擔水平荷載的大小取決于兩者的側向剛度之比,但不是一個簡單的比例關系,需要首先計算出結構的水平位移,然后根據墻體內力與位移的關系確定復合墻與剪力墻各自分擔的剪力、彎矩。
2 復合墻-剪力墻結構水平位移計算
2.1 計算模型
密肋復合墻-剪力墻混合結構中,不考慮剪力墻的剪切變形,考慮密肋復合墻則的彎曲變形和剪切變形,計算模型如圖2所示。當兩個子結構變形機制不同時,選定不同的子結構為分析對象,得出的位移微分方程在表達形式上有所不同,計算的繁簡程度亦有所區別,應以方便計算為原則選擇合適的分析對象。本文選擇密肋復合墻作為子結構1,以其為隔離體建立位移微分方程及進行水平位移公式的推導。
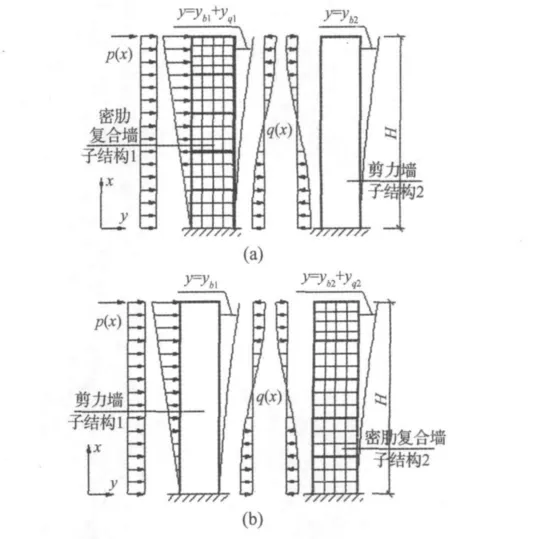
圖2 復合墻-剪力墻結構計算模型Fig.2 Calculating model of the structure
2.2 基本微分方程
如圖2(a)所示,子結構1(密肋復合墻)的變形由彎曲變形yb1和剪切變形yq1兩部分組成,根據Timoshenko剪切梁的彎曲變形、剪切變形與外荷載的基本關系[7]列出方程為:
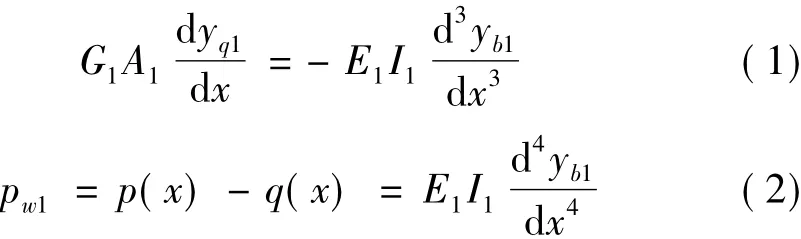
對于子結構2(剪力墻),其荷載與變形的關系為
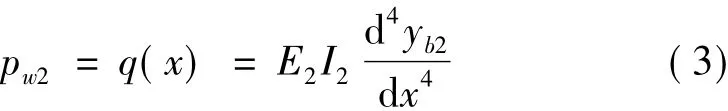
式中,E1I1、G1A1為子結構1的抗彎剛度、抗剪剛度,E2I2為子結構2的抗彎剛度,q(x)為兩個子結構之間的相互作用。
將式(3)代入式(2)得:
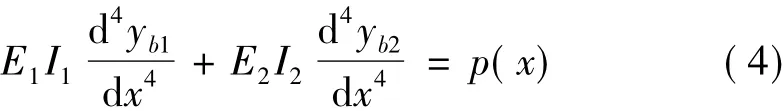
兩個子結構在任意位置的總水平位移相等,即yb2=yb1+yq1,代入上式消去yb2得:
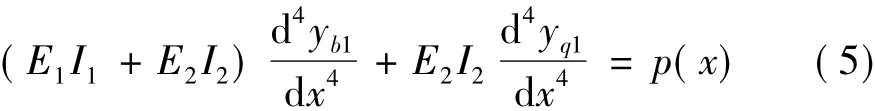
將式(1)兩邊對x微分三次,代入式(5)消去yq1
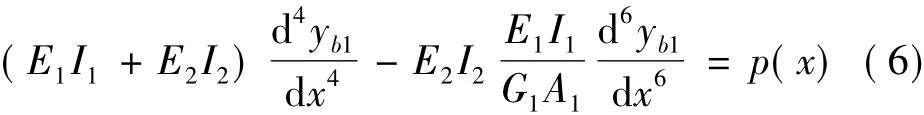

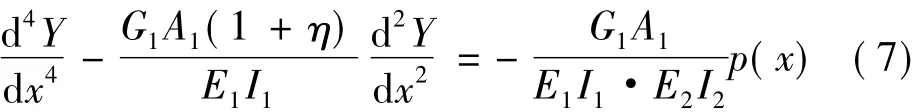
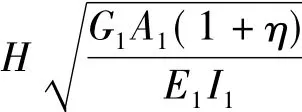
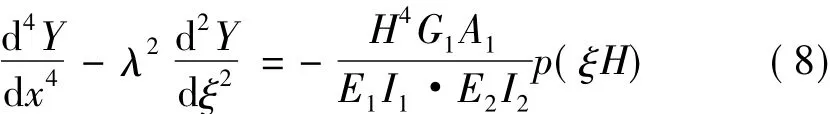
此式即為密肋復合墻-剪力墻混合結構的基本位移微分方程,理論上適用于密肋復合墻的抗彎剛度、抗剪剛度任意變化時其彎曲變形的求解。
如圖2(b)所示,當選擇剪力墻為子結構1,復合墻為子結構2時,得到以剪力墻為隔離體的彎曲變形微分方程見式(9)。比較式(7)與式(9)可知,后者不需要對位移方程使用變量換元法進行中間變量代換,但外荷載項中含有積分常數,需要結合邊界條件求得,求解過程相對復雜。
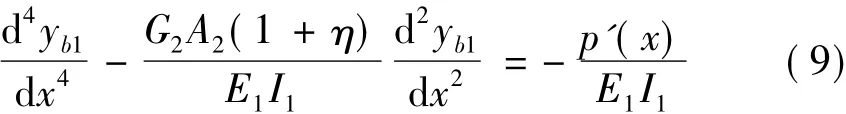
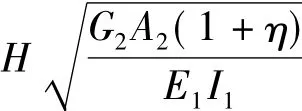
2.3 水平位移的解析解
對于四階常系數線性微分方程式(8),其解的一般形式為:
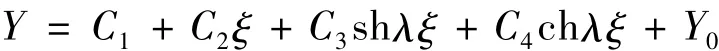
式中,C1、C2、C3、C4是待定常數;Y0為微分方程的特解,與外荷載的具體形式有關。
本文以常見倒三角形荷載為代表,給出水平荷載下密肋復合墻-剪力墻混合結構位移的具體推導過程。設倒三角形荷載為p(x)=qx/H=qξ,則式(7)的特解為:
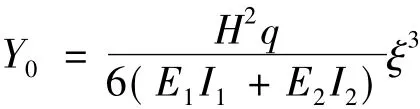
將Y0代入Y得到彎曲變形方程的一般解:
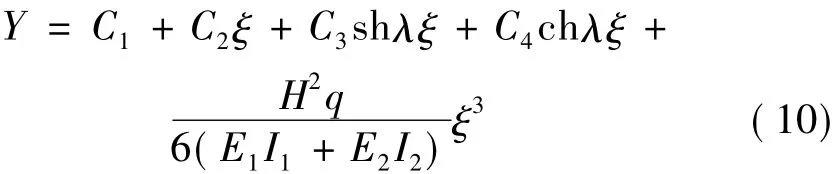
由Y對ξ積分兩次得到復合墻彎曲變形yb1的表達式:
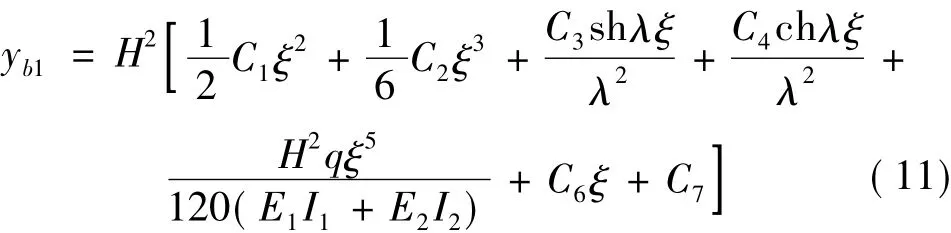
通過子結構1彎曲變形與剪切變形的關系得到其剪切變形yq1,由式(1)、式(11)得:
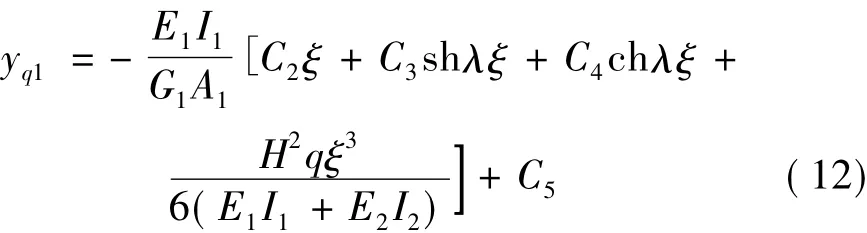
子結構1的彎曲變形與剪切變形之和即為子結構2的變形,同時也為復合墻-剪力墻結構的總水平位移,將yb1、yq1代入yb2=yb1+yq1整理得:
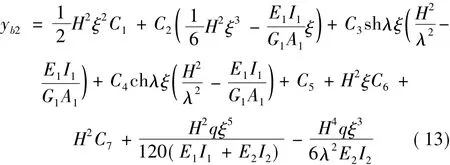
根據圖2(a)確定邊界條件,并將邊界條件寫成矩陣表達形式如下
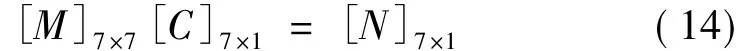
式中:
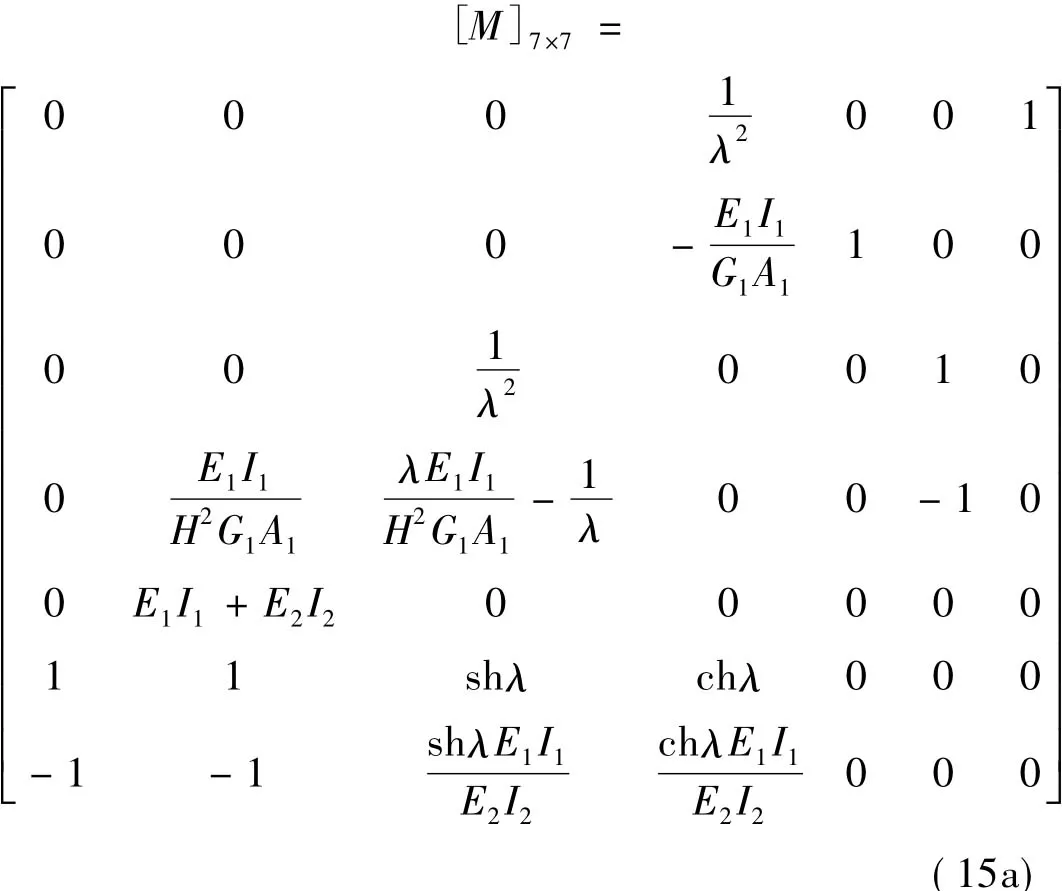
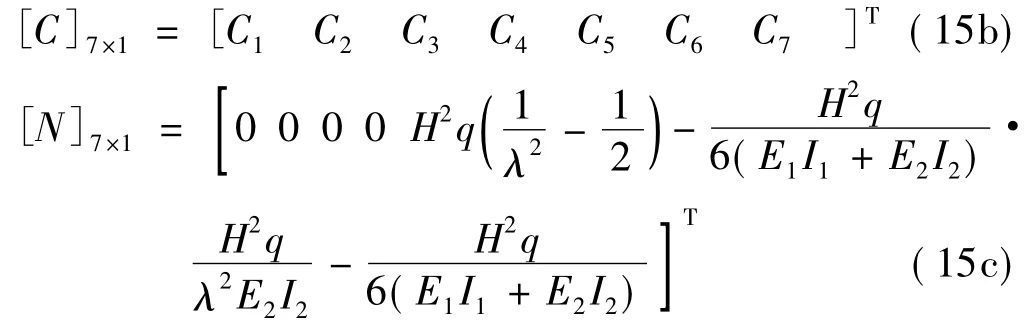
解矩陣方程式(14)得各待定系數為:
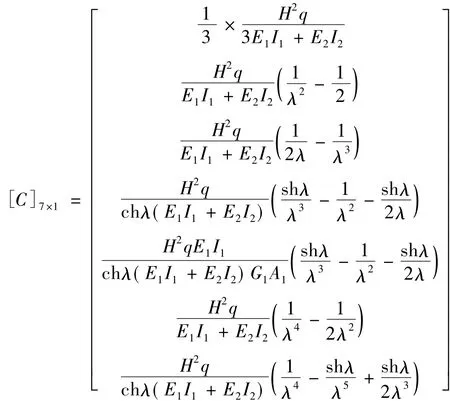
將系數C1~C7回代至式(11)~式(13),化簡得:
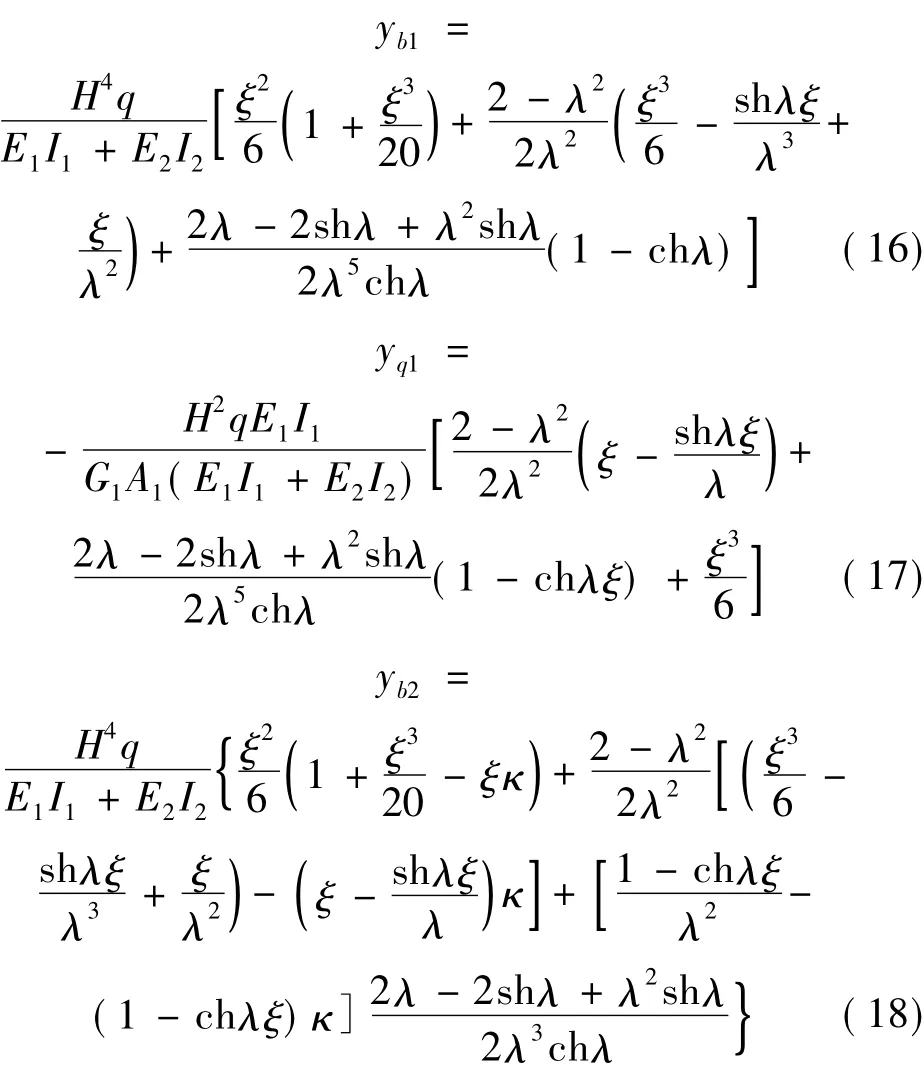
式中,κ=E1I1/H2G1A1。
至此,倒三角形荷載作用下密肋復合墻-剪力墻混合結構中各子結構彎曲變形、剪切變形及結構總水平位移的解析解全部求出。
當混合結構承受均布荷載、頂部集中荷載作用時,位移計算過程與承受倒三角形荷載作用的計算過程基本一致。根據子結構內力與變形關系,可以計算其內力,進而進行墻體截面抗震設計與校核。
3 算例分析
算例1分析復合墻-剪力墻結構與框架-剪力墻結構位移計算公式的相容性。
圖2(a)所示的子結構1,當取框架為密肋復合墻的特例時,混合結構轉變為一般框架-剪力墻結構,忽略框架部分的彎曲變形,假定其抗彎剛度E1I1→∞,則對混合結構特征值λ進行極限運算得:
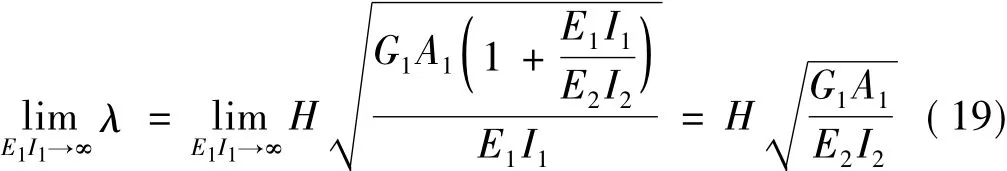
對混合結構中密肋復合墻的彎曲變形、剪切變形解析表達式(16)、式(17)進行E1I1→∞的極限運算,且代入式(19)給出的剛度特征值,整理得:
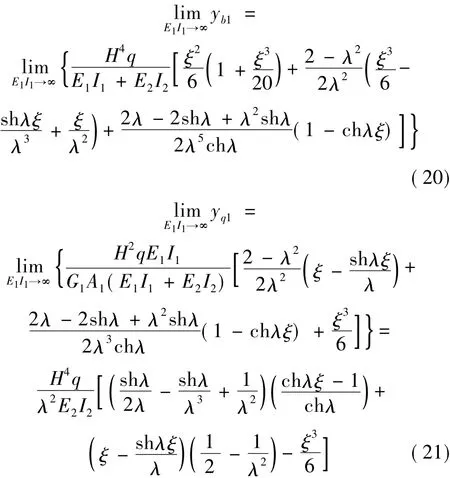
式(19)、式(21)即是人們所熟知的框架-剪力墻結構的剛度特征值和倒三角形荷載下水平位移的計算公式[8]。因此,框架-剪力墻結構可以視為密肋復合墻-剪力墻混合結構在密肋復合墻抗彎剛度取無窮大時的一種特殊表現形式,兩者的剛度特征值、位移計算公式是完全相容的。
算例2某10層復合墻-剪力墻結構,層高3.6 m,密肋復合墻、剪力墻厚均為200 mm。復合墻按工程中常用的密肋復合墻構造形式設計,單片墻體抗彎剛度和抗剪剛度為E1I1=6.2 ×1016N·mm2、G1A1=1.1×109N;單片剪力墻抗彎剛度為E2I2=7.9×1016N· mm2;剛度特征值λ=9.9,承受橫向倒三角形荷載作用,qmax=100 kN/m。
水平位移計算結果見圖3(a),分析可知:結構整體側移曲線呈現以彎曲變形為主的彎剪型特征,但密肋復合墻體的剪切變形在總變形中占有一定比重,不應忽略,本例中,剪切變形在復合墻下部三層占總變形的比重均超過20%,在三層至六層超過10%。與剪力墻的變形特點比較可知,當剪力墻高寬比>4時,可以忽略其剪切變形的影響,誤差不超過10%,而對于復合墻由于其剪切變形較大,高寬比達到6以上時,剪切變形所占比重才減小至20%以下。
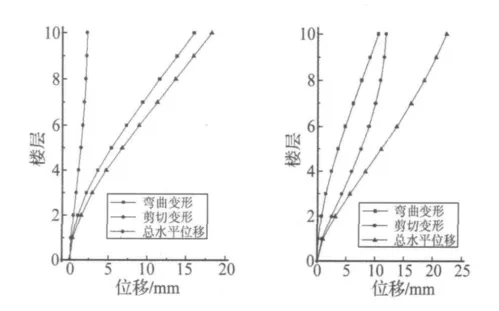
圖3 算例2位移計算結果Fig.3 Displacement calculation results of example 2
根據混合結構剛度特征值λ的定義,通過調整復合墻與剪力墻數量比例,或者調整復合墻抗彎剛度與抗剪剛度比例的方法,均可改變λ大小。現考察第二種方法對結構變形的影響,復合墻抗剪剛度取為原剛度的0.1倍,其它條件不變,計算結果見圖3(b),與圖3(a)比較可知:當復合墻抗剪剛度減小時,復合墻自身的剪切變形增大,本例中,復合墻剪切變形明顯大于彎曲變形,使得結構整體位移曲線趨近于框架-剪力墻結構的彎剪型特征。
4 結論
(1)分析了復合墻-剪力墻結構的協同工作機制,密肋復合墻的構造特點決定了墻體的抗彎剛度、抗剪剛度是與框格單元截面尺寸、框格構造形式等因素有關的變參數,復合墻剪切變形的計入導致復合墻與剪力墻之間的相互作用更為復雜。
(2)采用變形連續化方法建立了結構體系的位移微分方程,以倒三角形荷載為例推導了復合墻彎曲變形、剪切變形及結構總水平位移的解析表達式。密肋復合墻-剪力墻結構與框剪結構的剛度特征值、位移公式是完全相容的,后者可視為前者在復合墻抗彎剛度取無窮大時的一種特殊表現形式。
(3)一般中高層的復合墻-剪力墻結構側移曲線呈現彎曲變形為主的彎剪型特征,但復合墻體的剪切變形在總變形中占有一定比重,不應忽略。
(4)本文以密肋復合墻-剪力墻結構為例分析彎剪型(密肋復合墻)-彎曲型(剪力墻)雙重抗側力結構體系的位移計算方法,其思路同樣適用于其它彎剪型-彎曲型雙重結構體系的位移計算。
[1]河北省建設廳.密肋壁板結構技術規程(DB13(J)64-2006)[S].河北省工程建設標準,2006.
[2]張旭峰.密肋復合墻-剪力墻混合結構協同工作計算分析與實用設計方法研究[D].西安:西安建筑科技大學,2008.
[3] Xia L,Yao Q F,Chang P,et al.Seismic safety evaluation analysis of a new building structure with multi-ribbed composite wall structure[C].Proceedings of International Conference on Earthquake Engineering:The First Anniversary of Wenchuan Earthquake,2009:325-328.
[4]北京交通大學,等.具有多道抗震防線的耗能復合墻結構設計理論與關鍵技術研究[R].北京:北京交通大學,2009.
[5]黃 煒,張程華,姚謙峰,等.密肋壁板結構簡化計算模型對比分析[J].振動與沖擊,2009,28(7):187 -191.
[6]郭 猛,姚謙峰,黃 煒,等.水平荷載作用下密肋復合墻結構的變形計算[J].世界地震工程,2009,25(4):12 -17.
[7] Timoshenko S,Gere J.材料力學[M].北京:科學出版社,1990.
[8]包世華,張銅生.高層建筑結構設計和計算[M].北京:清華大學出版社,2005.

