帶滯變支撐懸臂輸流管的動力響應分析

黃 茜，臧峰剛，張毅雄，葉獻輝，蔡逢春

（核反應堆系統設計技術國家級重點實驗室，成都 610041）

近年來，輸流管內的軸向流引發的流致振動問題得到了廣泛的關注［1］。人們針對輸流管的非線性振動做了不少卓有成效的工作，就細長懸臂輸流管而言，這些工作主要包括：逐步建立并完善了輸流管的非線性運動微分方程［2，3］，研究了定常流與振蕩流作用下輸流管的穩定性分析［4－12］。

滯變支撐（Energy absorber）的恢復力是變形與速度的函數，在加卸載過程中不是沿著同一個路徑變化，而是形成如圖1所示的滯變曲線，這種特性能使滯變支撐在地震等緊急工況下大量耗能以保障結構安全。因此，這種支撐已被用于核工業，土木工程、建筑工程等領域。然而迄今為止，卻鮮有帶滯變支撐輸流管流致振動的研究報道。

本文基于能量法，將滯變支撐所做的虛功引入到管道的能量方程中，結合懸臂管道的不可伸長假設，導出了帶滯變支撐的懸臂輸流管的非線性運動方程。隨后，采用Matlab程序編制了數值計算程序，考察了該系統的動力學響應。

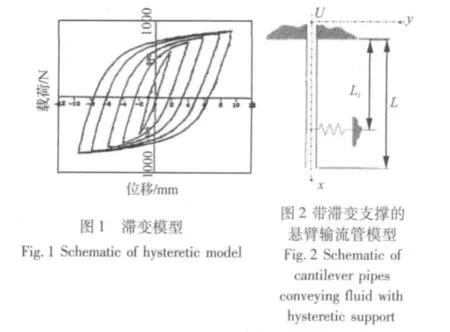
1 帶滯變支撐懸臂輸流管道的理論模型

懸臂管長為L，橫截面積為A，單位長度管道的質量為m，抗彎剛度為EI，流體的軸向流速為U，單位長度流體的質量為M，x表示管道橫截面位置，y表示管道軸線偏離平衡位置的位移，并引入沿管道軸線的曲線坐標s。假設在初始條件下管道沿x軸豎直放置，如圖2所示。

懸臂輸流管的基本假設為：① 流體不可壓縮，管內流速保持不變；② 管徑與管長之比很小，管道為歐拉梁；③ 不計管道的轉動慣量和剪切變形；④ 管道運動為平面運動且中心軸線不可伸長；⑤ 管道可以是大變形但應變很小。

基于Hamilton原理，帶滯變支撐的懸臂輸流管系統的能量方程為：

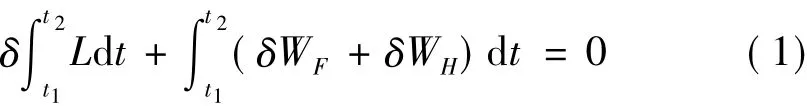
式中L=VP+VF－TP－TF，VP和VF是管道與流體的勢能，TP和TF是管道和流體的動能。第二個括號表示非保守外力虛功，其中，δWF為流體力對系統做功，δWH為滯變支撐對系統做功。

2 滯變支撐對系統做功

若沿輸流管軸線共布置了個P個滯變支撐，其中，第i個支撐距管道固定端的距離為Li，假設輸流管與滯變支撐連接點軸向變形很小，滯變恢復力的軸向分量可忽略不計。借助BOUC-WEN光滑滯變模型［13］，當管道受到外部激勵發生振動時，作用其上橫向滯變力可表示為：

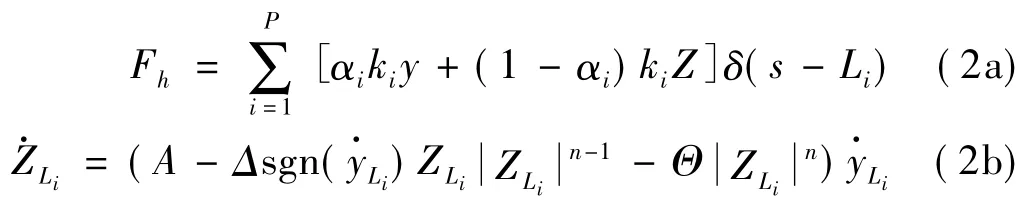
對第i個支撐而言，ki代表其初始剛度，αi為支撐屈服后剛度與屈服前剛度之比，yi為支撐點的橫向變形，Zi稱為滯變位移，A，Δ，Θ和n是控制滯變位移初始剛度、幅值和滯變形狀的滯變特性參數。只需調整這些參數，BOUC－WEN模型便可用來表達各種軟化、硬化滯變曲線，因此該模型又被稱為“萬能模型”。

本文僅考慮含1個滯變支撐的情形，即P=1，同時取滯變特性參數n=1。由虛位移原理可知，在t1～t2時間段內，滯變力Fh在虛位移δy上所做的虛功為：

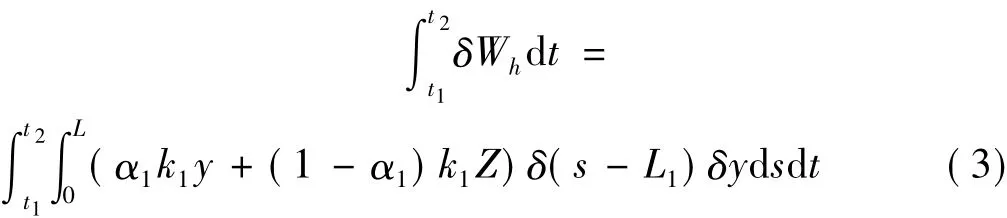
3 帶滯變支撐懸臂輸流管動力學微分方程及其求解

假設管道材料的耗散為粘彈性耗散，滿足Kelvin-Voigt模型，其應力－應變關系表示為：

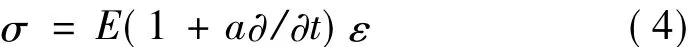
其中，a為粘彈性阻尼系數，對平面問題而言，管道的橫向位移與管長相比為一階小量，即：y=v～O（?），??1，本文方程中的變量精確到4階小量O（?4）。

將式（3）與式（4）代入式（1）結合式（2），通過分部積分、合并同類項等數學變換，可得到受滯變支撐作用的懸臂輸流管的非線性運動方程：

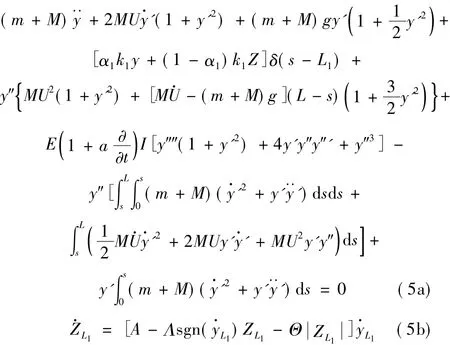
當α1=1時，方程（5a）第一行代表滯變恢復力的非線性項［α1k1y+（1－α1）k1Z］δ（s－L1）與滯變位移ZL1不再相關，簡化為線性項k1yδ（s－L1），此時，模型退化為帶線性彈簧支撐的非線性懸臂輸流管。

為便于計算與分析，引入下列無量綱量：

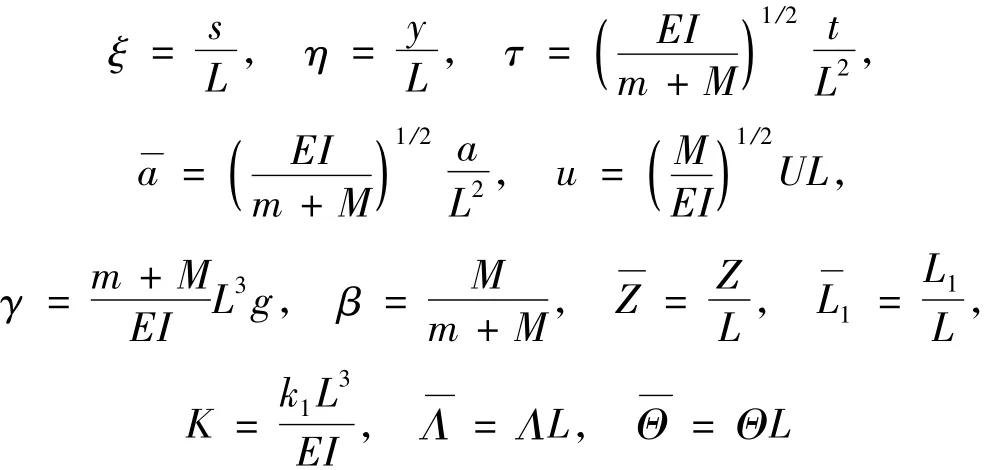
由于非線性運動方程為復雜的偏微分方程，不能直接求解，為此，作2階模態的Galerkin展開式：

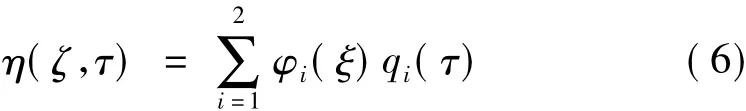
其中，qi為廣義坐標，φi為輸流管的振型函數，代入式（5）并無量綱化后有：

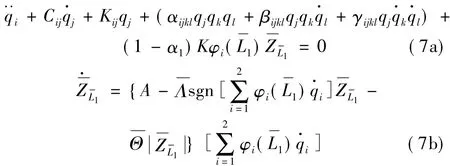
其中：

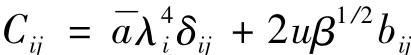
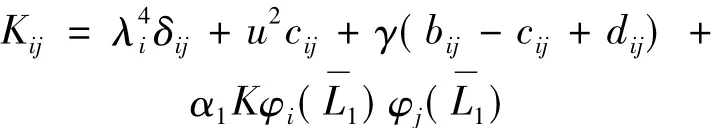
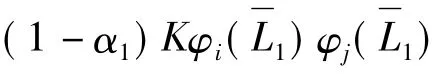
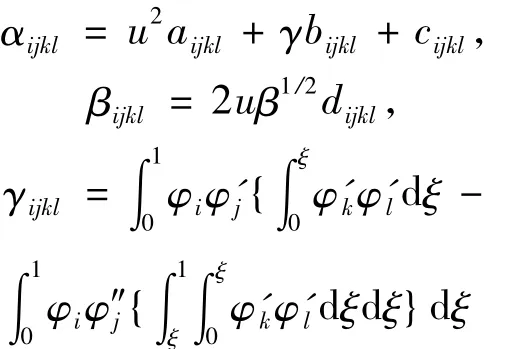
其余非線性項bij，cij，dij，aijkl，bijkl，cijkl及dijkl的詳細表達可參考文獻［14］。

4 算例分析

4.1 計算參數

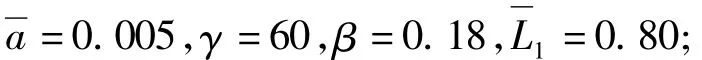
4.2 退化的帶滯變支撐懸臂輸流管模型

根據第3節推論，通過調整參數α1的取值，滯變支撐模型退化為線性支撐模型。為了證實該結論，本文畫出了帶滯變支撐（α1=1，K=100）的懸臂輸流管分叉圖，并與文獻［14］帶線性支撐懸臂輸流管（K=100）的結果進行了比較。分叉圖的橫坐標為輸流管內流速，縱坐標為懸臂管末端的穩態位移響應幅值，由此可觀察系統在不同流速取值點的運動狀態。為保證分叉圖的完整性，本文分別選取正、負位移作為初始條件（條件1∶q1（0）= －0.001；條件2∶q1（0）= －0.001，其余初始條件為零）進行數值計算，其結果呈現在圖3中。

本文計算結果表明，帶滯變支撐懸臂輸流管首次失穩為靜態失穩，失穩臨界流速為u=11.49；隨著流速增加，當u=12.42時，結構發生動態顫振失穩（文獻［14］靜態失穩為u=11.47，動態顫振失穩為u=12.43），結果幾乎完全一致，微小差別是數值計算引起的。同時，由圖3可知在8≤u≤22的整個流速范圍內，懸臂管末端的穩態響應幅值隨流速增加呈逐步增長趨勢兩結果也幾乎完全重合。由此驗證了本文模型的合理性與正確性。

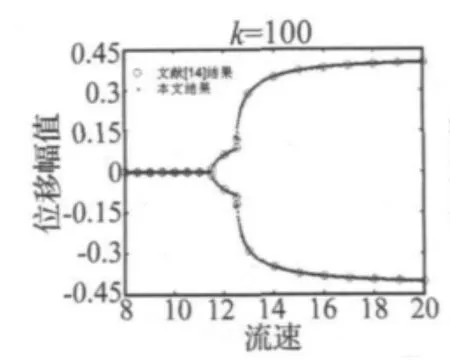
圖3 退化模型合理化驗證Fig.3 Validation of the degenerate model

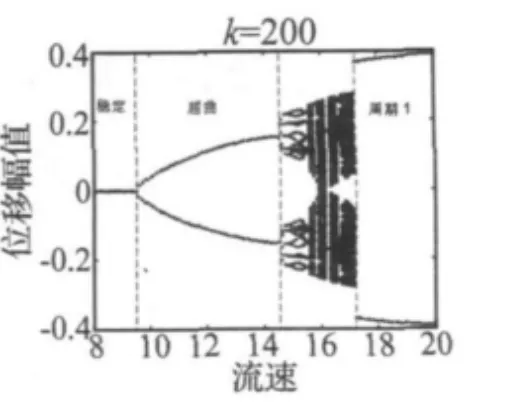
圖4 流速參數區域分叉圖Fig.4 Bifurcation diagram with fluid velocity

4.3 帶滯變支撐懸臂輸流管的響應分析

帶滯變支撐的懸臂輸流管存在極其復雜的動力學行為，圖4為K=200模型的分叉圖，從該圖可以看出：具有滯變特性支撐的懸臂輸流管存在極其復雜的動力學行為，圖4為K=200時系統的分叉圖，從該圖可以看出，隨著流速的增大，系統將由穩定變為不穩定，可能發生屈曲、周期、混沌等復雜響應。其中，u=9.5是系統的Pitchfork分岔點，當流速u＜9.5時，系統的能量耗散大于流體非保守力做功，平衡點為穩定的焦點，任何擾動經過一段時間后將回到平衡點；當9.7≤u≤14.5，系統發生屈曲失穩；管道相圖如圖5（a）所示；u=14.6是系統由靜態屈曲運動過渡到動態極限環運動的分界點，系統發生周期7的極限環振動，如圖5（b）所示；當流速略增長，位于u∈［14.7，14.9）的區間時，系統運動變為對稱的周期5極限環運動，如圖5（c）所示；此后，當14.9≤u＜15.4時，系統發生叉式分岔，兩種初始條件可得到兩種非對稱的周期5極限環，圖5（d）與圖5（e）分別為u=15時兩種不同初始條件下系統的相圖，此時的功率譜圖為圖5（f），不難看出，該流速的功率譜為離散的譜線，可以清晰的辨別出系統的振動頻率；同樣是u=15時刻，圖5（g）與圖5（h）為滯變支撐與管道交匯點對應的相圖與功率譜圖，通過與圖5（d）－圖5（f）的結果對比可發現，同一流速下輸流管各個部位的振動形式有顯著差異，但其振動頻率卻是相同的。在15.5≤u≤17.1的區間范圍內，系統振動將主要表現為混沌運動［圖6（a），6（c）］，其間夾雜著周期振動［圖6（b）6（d）］；由響應分叉圖可以觀察到，系統的振動幅值與主頻在流速點u=17.2處有明顯的跳躍，這種跳躍對應著系統振動性態的突然改變；此后，隨著流速的增大，管道的振動將維持周期1運動［圖6（d）］，而響應的振幅也將隨流速增加而逐漸增大。

4.4 滯變支撐剛度對懸臂輸流管穩定性的影響

支撐的剛度能刻畫運動約束的軟硬程度，這種軟硬程度將會引起系統的動力學行為發生改變。K=100，K=150，K=200，K=250 與K=300 對應的系統響應分叉圖分別如圖7（a），圖7（b），圖4，圖7（c）及圖7（d）所示。

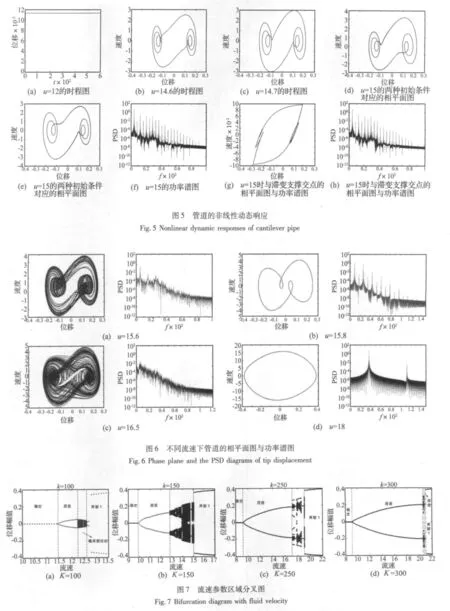
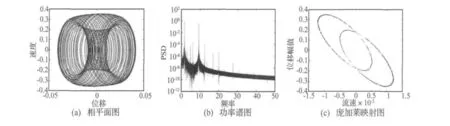
圖8 系統的概周期運動（K=100；u=12.5）Fig.8 The quasiperiodic oscillation for the system with K=100；u=12.5

帶滯變支撐懸臂輸流管除了發生屈曲、周期、混沌運動外，還可能發生概周期運動：若K=100，且流速為12.3≤u≤12.6時，系統的相平面圖顯示為紊亂且不重合的軌跡［圖8（a）］，這種軌跡只可能存在于混沌或概周期運動中，為了鑒別系統真實的運動狀態，需要作出此時系統的功率譜與龐加萊映射圖：功率譜圖［圖8（b）］表明該響應具有顯著的周期運動特性，而其龐加萊映射［圖8（c）］呈現為兩個封閉的橢圓圖案，仿真結果表明，系統響應為概周期運動。

通過對分叉圖的比較可以發現，當K≥100時，隨著無量綱化支撐剛度K的增加，系統發生首次失穩的臨界流速值會逐漸降低，而發生大幅跳躍的流速值會逐漸增加。此外，系統出現復雜響應（多周期、概周期與混沌運動）的參數范圍將逐漸減小，直至系統不再出現復雜響應。

總之，剛度的變化不僅使使得系統的分叉類型、分叉方式與分叉路徑發生了的顯著變化，并使其出現復雜響應的參數范圍發生了改變，也改變了周期運動的周期數。因此，運動約束的軟硬程度對系統的動力學響應有較大影響。

5 結論

利用Hamilton體系的變分原理，導出了帶滯變支撐懸臂輸流管的非線性運動方程，通過數值模擬與算例分析，可得以下幾點結論：

通過滯變支撐退化模型與現有文獻結果比較，證實了本文模型的合理性與有效性。

滯變支撐懸臂輸流管表現出豐富的動力學行為，隨著流速的增大，系統將由穩定變為不穩定，系統的運動形式可能為屈曲失穩、周期、概周期，混沌運動等。

支撐剛度是決定系統穩定性的重要因素之一。隨著支撐剛度的增加，系統發生首次失穩的臨界流速值會逐漸降低，發生跳躍的流速值反而會逐漸增加；此外，系統出現復雜響應的參數范圍將逐漸減小。

［1］任建亭，姜節勝.輸流管道系統振動研究進展［J］.力學進展，2003，33（3）：313－324.

［2］ Lee S I，Chung J.New non-linear modeling for vibration analysis of a straight pipe conveyingfluid［J］.Journal of Sound and Vibration，2002，254（2）：313－325.

［3］ Semler C，Li G X，Paidoussis M P.The nonlinear equations of motion of pipes conveying fluid［J］.Journal of Sound and Vibration，1994，169（5）：577－599.

［4］Wadham-Gagnon M，Paidoussis MP，Semler C.Dynamics of cantilevered pipes conveying fluid.Part1： Nonlinear equations of three-dimensional motion［J］.Journal of Fluids and Structures，2007，23：545－567.

［5］Paidoussis M P，Semler C，Wadham-Gagnon M.Dynamics of cantilevered pipes conveying fluid.Part 2：dynamics of the system with intermediate spring support［J］.Journal of Fluids and Structures，2007，23：569 －587.

［6］ Modarres-Sadeghi Y，Semler C.Dynamics of cantilevered pipes conveying fluid.Part 3：Three-dimensional dynamics in the presence of an end-mass［J］.Journal of Fluids and Structures 2007，23：589－603.

［7］Jin J D，Song Z Y.Parametric resonances of supported pipes conveying pulsating fluid［J］. JournalofFluidsand Structures，2005，20 763 －783.

［8］Wang L.A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid［J］.Journal of Non-Linear Mechanics 2009，44：115－121.

［9］包日東，聞邦椿.分析彈性支承輸流管道的失穩臨界流速［J］.力學與實踐，2007，29（4）.24 －28.

［10］包日東，金志浩，聞邦椿.一般支承條件下輸流管道的非線性動力學特性研究［J］.振動與沖擊，2009，28（7）：153－157，186.

［11］金基鐸，楊曉東，鄒光勝.兩端支承輸流管道的穩定性和臨界流速分析［J］，機械工程學報，2006，42（11）：131 －13.

［12］金基鐸，楊曉東，張宇飛.固定約束松動對輸流管道穩定性和臨界流速的影響［J］.振動與沖擊，2009，28（6）：95－99.

［13］歐進萍，王光遠.結構隨機振動［M］.北京：高等教育出版社，1998.

［14］ Paidoussis M P.Fluid-structure interactions［M］.London：ACADEMIC PRESS，1998.