經驗模態分解法在電動機鐵心故障檢測中的應用

曾方

(成都航空職業技術學院，成都 610100)

0 引言

三相異步電動機的定子鐵心故障是電動機故障中最嚴重的故障之一。如果只是定子鐵心發生了變形、松動或偏心，維護人員是很難發現電動機的異常情況的。但這些異常同樣將導致電動機運行發生嚴重事故。

為了早期發現這些出隱患，考慮到電動機鐵心故障總會導致電動機的振動，提出了一種通過檢測電動機振動信號，用經驗模態分解法分析這一振動信號，使維護人員盡早發現電動機運行故障的振動檢測分析法。通過實驗證明在一定程度上是一種行之有效地方法。

1 EMD和Hilbert變換的信號分析方法

1.1EMD 分解法

經驗模態分解(Empirical Mode Decomposition:EMD)［1］方法的主要思想是把信號分解獲得有限數目的本征模態函數(Intrinsic mode function:IMF)。由于瞬時頻率時間的單值函數，所以在求瞬時頻率時，對應的信號應受到一定的限制，而且由于在任何一個時刻只有一個頻率值，所以此時刻信號應該只有一個分量。用EMD方法一般采用如下三個步驟:

(1)找出原始時間序列，序列x(t)上至少存在有兩個極值點，一個局部極大值和局部極小值，如果利用三次樣條曲線插值的方法這兩個極值點，就可分別得到上下兩個包絡線，即極大值包絡xmax(t)和極小值包絡xmin(t);

(2)由于信號的所有數值都在兩個包絡線之間，因此求取每個時刻的極大值包絡xmax(t)和極小值包絡xmin(t)的平均值，即可獲得瞬時平均值m(t)，用式(1)表達

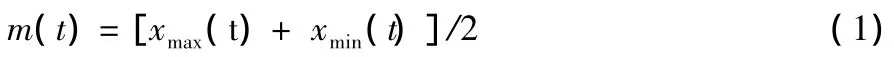
(3)再用原始時間序列x(t)減去瞬時平均值m(t)，就可得到一個去掉低頻的新數列h(t)，用式(2)表達

獲得新數列h(t)后，還要對其進行篩分，以此可消除h(t)中的一些附加波，同時還可以波的輪廓更加對稱。

可以重復篩分多次，如果對稱于局部零均值，并且有相同的極值點與過零點的數列h(t)就是一個滿足固有模態信號的條件的固有模態信號IMF，否則重復(3)式步驟迭代，直到獲得滿足必要條件的數列。

將得到的第一個本征模態函數用IMF表示1并記為imf1(t)。

當式(3)中的分量mk或hk小于預定值時，或當剩余分量hk變成單調函數時，將不能再篩選出基本模式分量，則可停止篩選，將式(2)與式(3)相加，得到原序列如式(4)所示

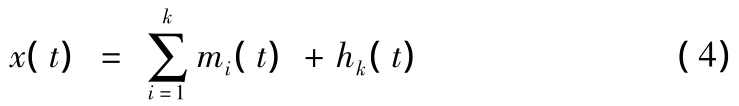
到此已經把原始數據分解成k個模態分量及一個剩余分量mk。

通過EMD分解得到固有模態信號IMF后，對其做希爾伯特變換，計算變換后的瞬時頻率，即可得到Hilbert譜，再對波譜進行分析比對，找出電動機鐵心故障點。

1.2 Hilbert變換和 Hilbert譜

首先對每一個IMF分量進行Hilbert變換，變換方法如式(5)所示

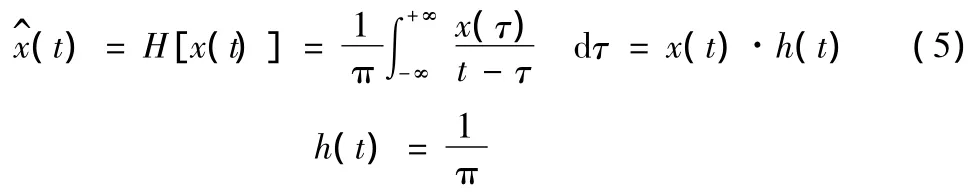
式(5)中x(t)為實信號，如果以它作為實部，x(t)的Hilbert變換(t)作為虛部，就構成了一個復信號z(t)，也就是解析信號或稱之為信號的預包絡線，用式(6)表達

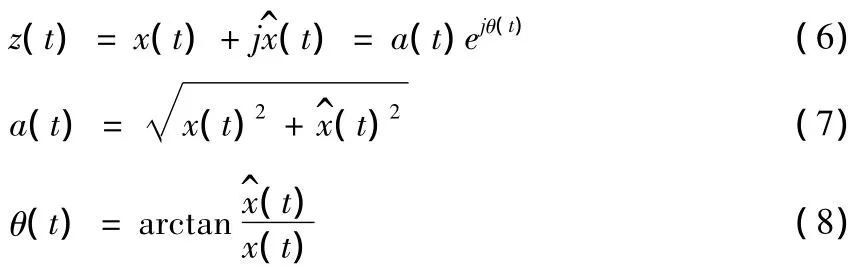
瞬時頻率按下式計算

用上述希爾伯特方法對式(4)中的每一個IMF分量都進行變換之后，就可以把解析信號表示為式(10)所示

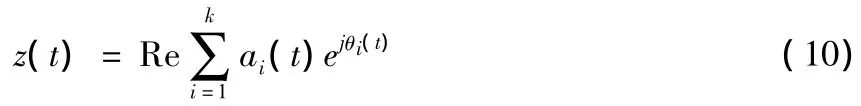
式(10)是一極坐標形式的表達式，明確地表示了信號瞬時振幅和瞬時相位之間的關系。式中省略了殘余函數m(t)。

Re表示取實部得到的幅值函數。由上述變換得到的是振幅和頻率都是時間函數，如果把其中的振幅表轉換到頻率－時間平面上，就可得到Hilbert變換普，用式(11)表示為

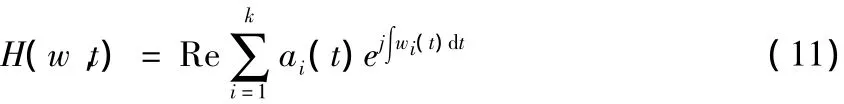
再對H(w，t)對時間時行積分，就是希爾伯特的邊際普，用式(12)表示為

通過希爾伯特邊際普所得到的信號頻率與傅里葉分析中得到的信號頻率，它們的物理意義是完全不同的。希爾伯特變化特別強調局部屬性，從而避免了傅里葉變換中，為了擬合原始數列而產生的許多實際當中并不存在的高低頻成分。

2 電機振動分析方法

大多數的電動機，如果發生故障，都會伴隨著振動和噪音出現，電機振動分析方法就是利用這些振動和噪音，在電動機的體外進行檢測的一種方法。

將一振動傳感器安裝在電動機的機身上，用來監測電動機運行中的各種振動信號，將獲取到的振動信號，進行時域、頻域特性分析，這些信號中包括了繞組和鐵心振動信號的頻譜、功率譜、能量譜等，從而可繪制出不同運行情況下的參數曲線，工作人員可以從不同時刻的參數曲線上獲取繞組或鐵心的運行信息，診斷繞組和鐵心的工作狀態，預測可能發生的故障，從而協助工作人員制定維護方案［2］。

在線測量電動機表面的振動信號，分析振動信號從而監測判斷鐵心、繞組的運行狀況和故障情況，這種常用于變壓器故障檢測的方法用于電動機的檢測，作為一種嘗試。

3 電動機振動信號分析

電動機異常振動的原因主要由于鐵心發生變形、偏心、松動，定子繞組發生斷線、接地擊穿、匝間短路、接線錯誤、三相電流不平衡等造成。通過分析，這些事故隱患均可以通過鐵心振動加速度的變化反映出來。

3.1 電動機振動信號的獲取

為了降低成本，本實驗選用了一臺10 kW的三相籠形異步電動機作為實驗對象。通過傳感器分別測量電動機在正常和非正常(人為松動緊固螺絲等)情況下電動機的鐵心振動加速度信號。電動機振動信號的測量示意線路如圖1所示。

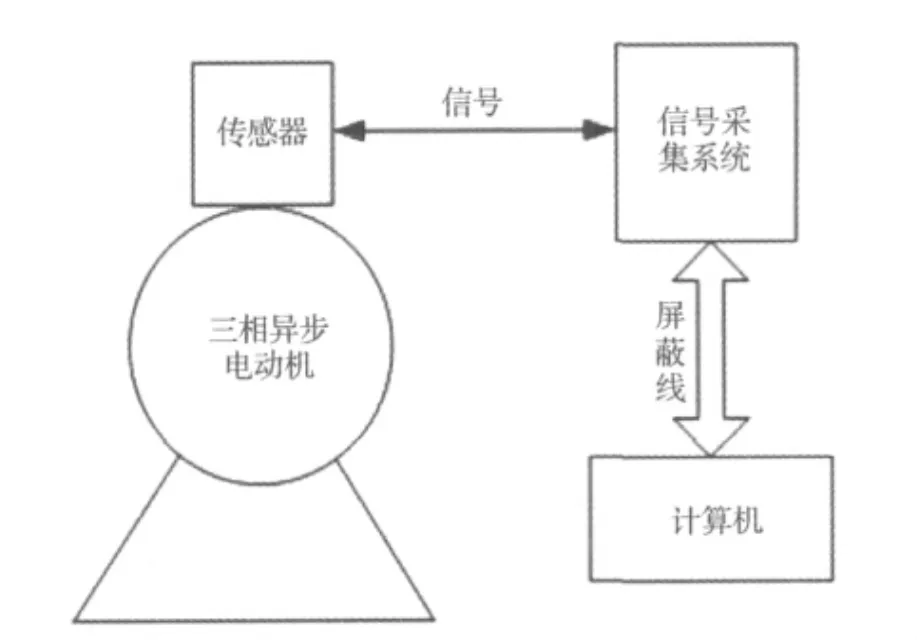
圖1 電動機振動信號測量示意圖

傳感器的安裝位置和安裝牢固程度是能否獲得正確電動機振動信號的關鍵，所以一定要將傳感器用磁體牢固地吸附在電動機機身表面。檢測振動信號時是很容易同時引入干擾信號，因此還要將傳感器的輸出信號線，通過屏蔽線連接到信號放大電路的輸入端。

當電動機運行時，傳感器接受并傳送這一振動信號，將所測得的振動信號送入示波器顯示、存儲，或者直接通過數據采集裝置存儲在計算機中。

3.2 鐵心振動信號及本征模態函數imfs

通過圖1所示的實驗裝置，可以得到電動機鐵心正常和故障時的振動加速度信號。從時域圖中只能看到的故障后振動加速度信號幅值與正常狀態時稍微有些不同，如果只憑這些微弱的區別是無法判斷出電動機是否工作在正常和故障狀態。只有對信號進一步分解處理以提取更詳細的故障特征信息，才能獲得準確的判斷依據。

改進的方法是，先用經驗模態分解的方法分別對電動機正常運行和故障運行狀態下的振動信號進行分解，得到固有模態信號IMF，用此信號構建出希爾伯特譜。再建立“運行狀態—能量特征”的一一對應關系，把變換后的信號幅值顯示在三維空間。這樣就獲得了監測信號的內在本質特征，最終可以獲取能夠監測電動機的運行狀態并能夠用于維護的特征信息。

采用經驗模態分解鐵心正常振動信號和鐵心異常振動信號，得到如圖2、圖3所示。圖中包含6個imfs信號和一個剩余分量imf7。可以看出，隨著EMD分解法的迭代去除包絡均值的低頻成分的進行，分解得到的imfs信號頻率在逐漸減小，其中imf1為高頻信號成分，最重要的是imf2～imf5這一段，它們是包含了鐵心運行狀態信息的低中頻段的信號分量，也就是電動定了繞組內電磁力引起振動信號的基頻分量各高次諧波分量，因此它們正好反應了電動機的振動狀態。imf7為剩余分量。

將振動信號中imf2～imf5的相位和擬合一次獲得一個多項式并繪出其曲線，進一步分析該多項式曲線得出，在磁致伸縮作用下的鐵心振動主要發生在300 Hz～500 Hz頻率段以及高次諧波段，而且信號的本征模態的頻率越高，瞬時頻率波動就越大。這為進一步分析電動機振動信號的三維Hilbert譜提供了依據。

3.3 鐵心振動信號的三維Hilbert譜

由于Hilbert譜能夠非常清晰、直觀地表示出鐵心振動信號的能量在特征頻率、時間上的分布情況，因此對圖2和圖3所示的IMF信號分別進行希爾伯特變換，當振幅取分貝后作為衡量單位，即可得到正常狀態下和故障狀態下振動信號的Hilbert譜，如圖4和圖5所示。

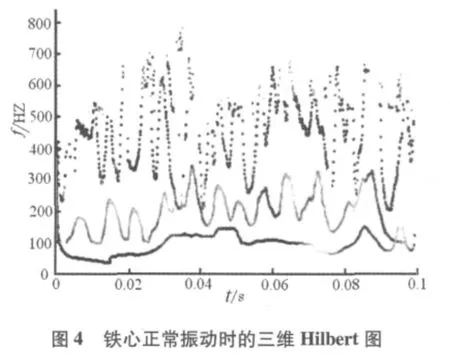
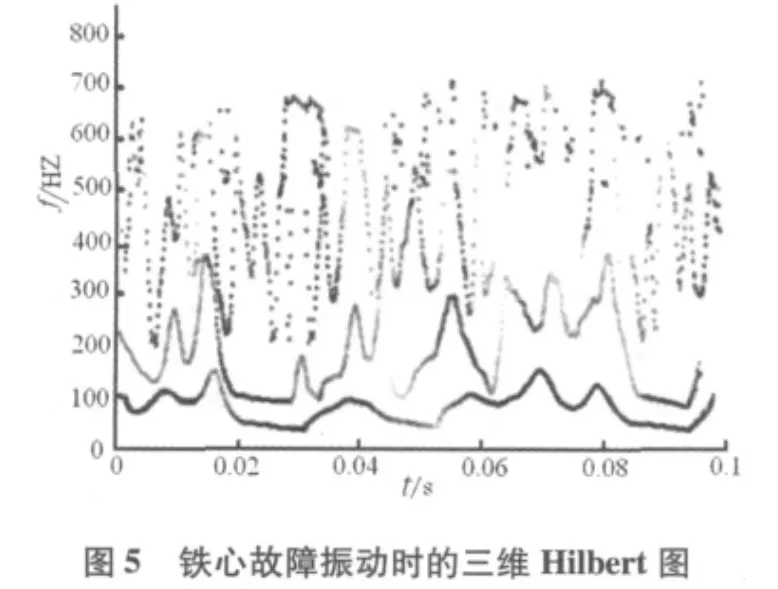
分析比較兩圖可以發現，當鐵心發生故障時，振動基頻通常出現在100Hz左右;振動的2次諧波、4次諧波為高頻段800～9000Hz段。

還可以從能量分布圖可以看出，振動信號的能量分布，隨Hilbert信號頻率的變化而變化，尤其是高頻段最為明顯，接近25dB的能量增加。這說明，當鐵心發生故障后，能量變化回大，振動信號的高次諧波的振動能量分布變得非常豐富，如果這一分布越豐富，說明鐵心故障越嚴重。

還可以看出，鐵心故障的Hilbert譜譜峰主要出現在振動基頻100Hz及其整數倍的頻率處，鐵心振動的能量主要集中在500Hz附近。

通過分析三維Hilbert譜能量分布特征，還可以提取出有效而且簡便的狀態指紋，同樣可以判斷出電動機鐵心是否發生故障以及故障嚴重程度。

4 結論

由實驗數據可以看出，應用EMD方法分解電動機鐵心振動信號，提取電動機運行狀態特征信息，再利用振動信號imfs的能量分布變化，能夠對電動機運行狀態做出診斷，監測電動機運行狀況的變化，進一步為電動機狀態維修提供參數依據。但這種方法會產生邊界誤差，隨著EMD過程的進行將向內污染數據，造成分解結果的誤差，因此最好再采用基于預測模型進行端點延拓可以有效的控制EMD篩選過程的邊界誤差。

［1］ Huang N E，S R Long，et.The empirical mode decomposition and spectrum for nonlinear and non-stationary time series analysis［J］.Proc R Soc London A，1998:454－903.

［2］ 陳奎.變壓器短路試驗方法與發展［J］.變壓器，2000，37(1):49－52.

［3］ Li Hongsheng，Li Zhengqin，et.Implement based on DSP［J］.7th International Conference on:499－502.

［4］ 王江萍.機械設備故障診斷技術及應用［M］.西安:西北工業大學出版社，2001:499－502.

［5］ 洪飛，吳志美.基于小波的Hurst指數自適應估計方法［J］.軟件學報，200516(9):1685－1689.

［6］ 程軍圣，楊宇，于德介.基于MODWPT的Hilbert譜及其在齒輪故障診斷中的應用［J］.振動與沖擊，2007，26(17):42－43.

［7］ 金勇，劉佳宇.電動機振動原因和故障的處理［J］.齊齊哈爾大學學報，2007，12(16):36－37.

［8］ 于明湖，張玉秋.雙定子直線振蕩電機諧振特性分析［J］.電機與控制學報，2010，8(1－6).

［9］ 陳剛，張朝霞，莊良杰.小波域中值濾波器在陀螺尋北儀中的應用［J］.天津大學學報，2006，39(7):797－800.

［10］ 梁武科，趙道利，馬薇，等.基于粗糙集RBF神經網絡的水電機組故障診斷［J］.儀器儀表學報，2007，28(10):1806－1810.