瞬時對稱分量法及其在故障暫態測距中的應用

高作毅 羅顯通 黃翰

(1.重慶市電力公司璧山供電局，璧山 402760;2.四川電力設計咨詢有限責任公司，成都 610016)

0 引言

對于三相系統，由于各相間存在電磁耦合，直接在相域進行故障計算十分困難。為簡化計算，一般需要進行相模變換以實現解耦。常用的相模變換有對稱分量變換、派克變換、克拉克(E.Clarke)變換，卡倫鮑厄(Karrenbauer)變換等［1～4］。其中對稱分量法被廣泛用于繼電保護、故障分析、無功補償、系統建模、系統辨識等電力系統各種領域。

傳統的對稱分量法定義在頻域范圍，處理三相電流、電壓的相量，只適用于電力系統穩態分析。瞬時對稱分量法定義在時域范圍，利用電流、電壓的瞬時值進行對稱變換，因此可分析電力系統的暫態過程。文獻［4］提出一種根據旋轉磁場原理將參考坐標置于電機定子側的瞬時對稱分量變換，然而變換矩陣中仍采用復數相位因子，得出的序分量為復數變量。文獻［5～6］在時域中用120°移相操作代替變換矩陣中的復數相位因子進行變換，其核心是借助鎖相環(EPLL)提取出的基波相位實現移相，但鎖相環的計算會帶來一定的延時，不利于序分量的實時提取。文獻［7］利用電壓或電流瞬時值構造旋轉相量，采用傳統對稱分量變換矩陣與旋轉相量相乘求出以復數形式表示的序分量，最后提取其虛部得瞬時值。

本文提出的瞬時對稱分量變換法，通過三角函數變換分解出旋轉相量的實部和虛部，再利用簡單的移相算法對三相電流、電壓瞬時值進行相應的變換，從而獲取各個序分量的瞬時值。將該法用于電力系統故障分析，能在故障暫態過程中快速計算故障距離，動模試驗及matlab分析驗證了該方法的有效性和實用性。

1 瞬時對稱分量變換的基本原理

1.1 瞬時序分量的表示方法

設三相電流的瞬時值為幅值和相位不隨時間變化的正弦周期信號，其表達式為

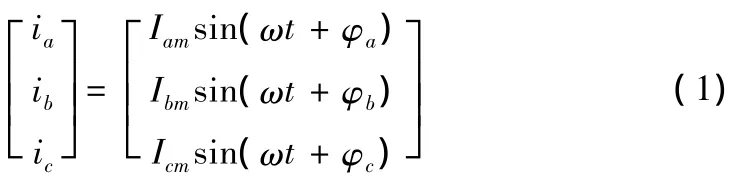
式中 ia、ib、ic分別為三相電流瞬時值;Iam、Ibm、Icm分別為三相電流的幅值;φa、φb、φc分別為三相電流的初相位。

由于對稱分量法運用旋轉相量進行變換，而ia、ib、ic對應的旋轉相量分別為，其表達式為

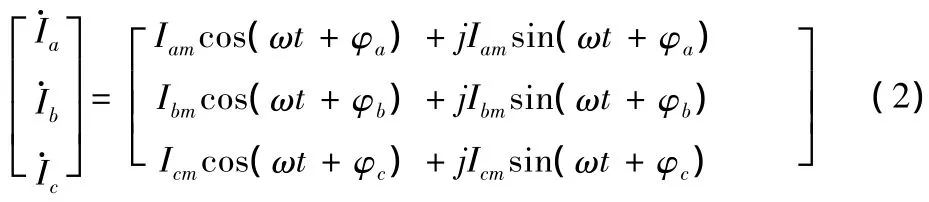
以A相為例，則復平面上所對應的旋轉相量圖如圖1所示。

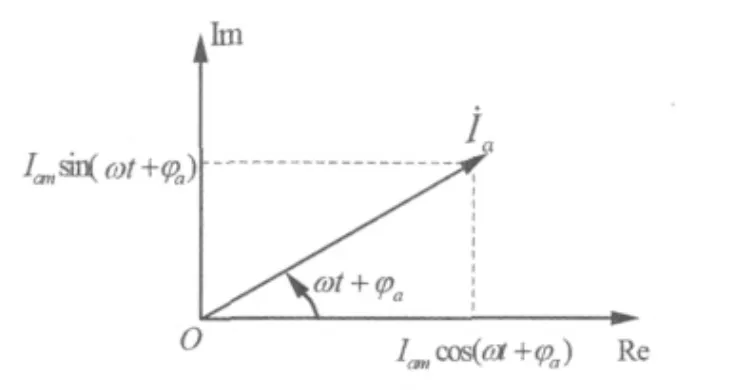
圖1 旋轉相量

由對稱分量法知，三相電流相量與其對稱分量之間的關系為

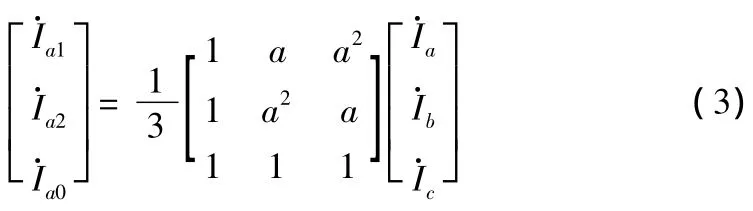
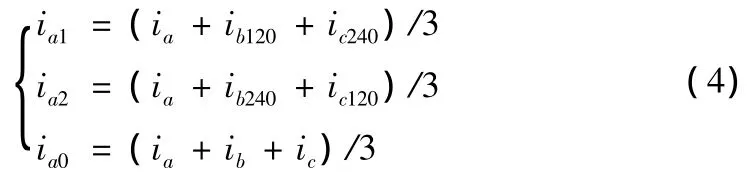
式(4)中ib120、ib240分別表示將B相電流瞬時值的相位向前移動120°和240°;ic120、ic240分別表示將C相電流瞬時值的相位向前移動 120°和 240°。

以B相電流瞬時值為例，運用三角函數分解法，將其相位前移120°可表示為

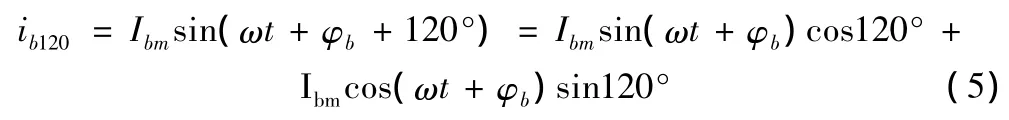
即

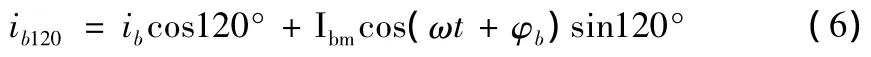
1.2 相量實部的求取

以B相電流為例，其瞬時值可表示為

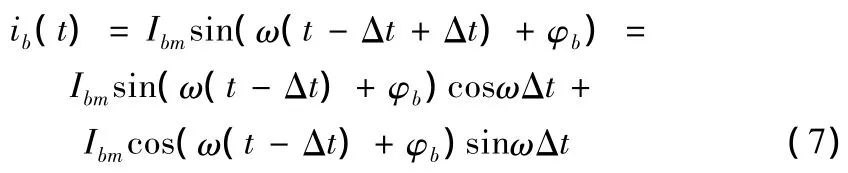
即

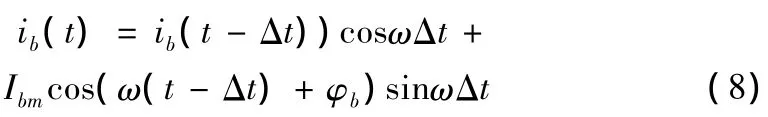
移相變換得

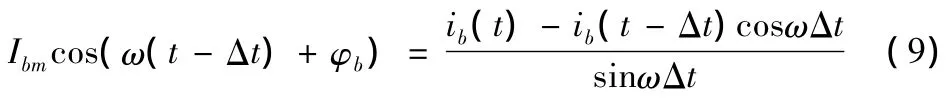
又

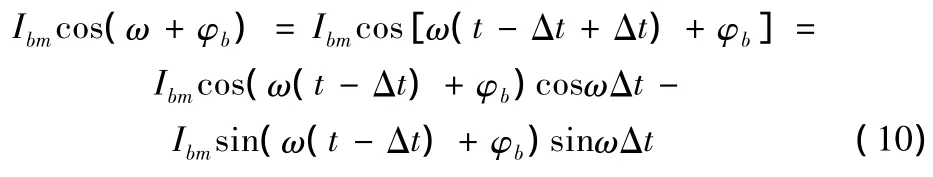
則將式(9)代入式(10)可得

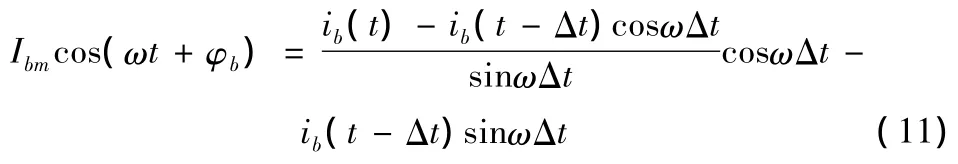
將式(11)代入式(6)可求出ib120。同理可求出ib240、ic120和ii240，最后將所得結果代入式(4)可得瞬時序分量的值。

2 基于瞬時序分量的暫態故障測距方法

2.1 基本思路

在分析三相對稱系統的暫態過程時，通常借助對稱分量變換將三相線路轉換為單相線路求解。當線路上發生短路故障，利用故障點的序分量邊界條件可方便的進行故障分析［8－14］。由于故障時系統電感電流和電容電壓不能突變，將會產生除基波分量以外隨時間衰減的高頻分量和直流分量，傳統的對稱分量變換針對穩定周期信號的相量提取，對于故障暫態信號的提取存在較大的誤差，而瞬時對稱分量法能實時提取序分量瞬時值，有利于實時分析系統故障。本文以線路發生兩相短路故障為例，提出一種利用瞬時序分量進行暫態故障測距的方法，基本思路是通過序分量邊界條件建立故障網絡時域微分方程，利用瞬時對稱分量變換求出方程中的瞬時序分量，最后通過最小二乘法求解故障距離［15］。

2.2 暫態測距原理

圖2為兩相相間短路和兩相短路接地故障。

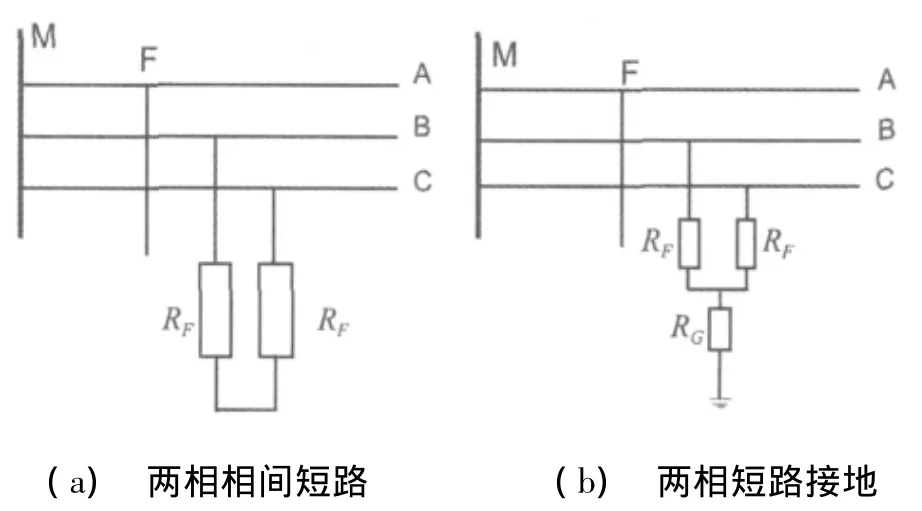
圖2 兩種短路故障模型

若忽略輸電線路分布電容，則對于這兩種故障模型 ，可分別寫出正、負序網絡的微分方程

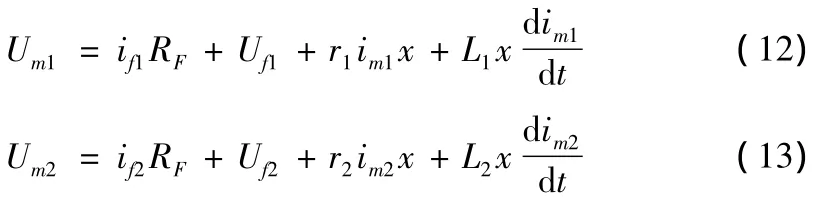
式(12)、(13)中 Um1、Um2、im1、im2分別代表測量端 M 處的正、負序電壓和電流瞬時值;Uf1、Uf2、if1、if2分別代表 F處的正、負序電壓和電流瞬時值;r1、r2、L1、L2分別為線路單位長度的正序、負序電阻和電感;x為測量點與故障點之間的距離。

圖2中，兩相相間短路故障的邊界條件為Uf1－Uf2=0;兩相短路接地故障的邊界條件為Uf1=Uf2=Uf0。因此將式(12)、(13)左右兩邊分別相減，并考慮到正、負序電阻、電感參數分別相等，整理可得

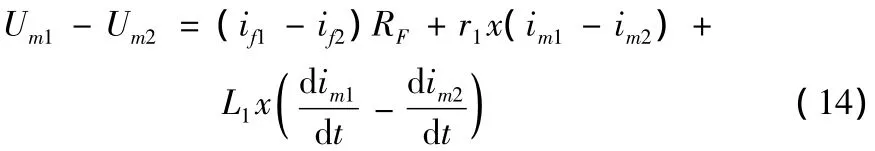
由于故障點的電流不能直接檢測，因此假設故障點各序電流的故障分量和保護安裝處各序電流的故障分量具有相同的相位，即兩者之間存在K倍關系，其中K為實數，其值由故障點兩端的網絡結構參數決定。采用該假設的原因有三點:其一，本文的研究對象為配電網，負荷側的短路電流很小，可近似認為故障點短路電流為送電側電流;其二，由疊加定理知線路上的故障電流為正常分量與故障分量的疊加，而短路點電流僅含故障分量，可近似認為與送電側電流故障分量同相;其三，兩相短路的接地電阻并不影響本文算法，而相間過渡電阻通常較小，對于本文假設所帶來的誤差不大。

根據假設將故障點的正、負序電流故障分量分別用測量點的正、負序電流故障分量表示

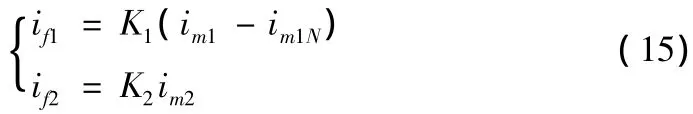
式(15)中im1N為系統正常運行時測量點的正序電流瞬時值;K1、K2為實數，考慮到正、負序網參數相同，因此K1=K2;將式(15)代入式(14)

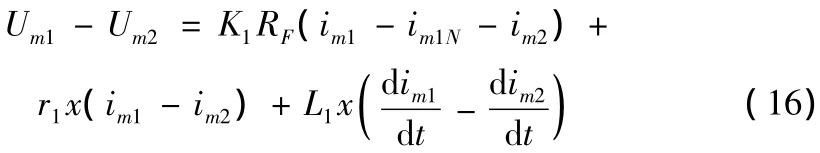
式(16)中將K1RF和x作為未知量，理論上只需故障后的兩個點即可確定故障位置，但考慮到減小偶然誤差對測距精度的影響，應增加點數，運用最小二乘法辨識出故障距離。

3 動模試驗驗證

為了驗證瞬時對稱分量變換及其在故障暫態測距中的正確性和可行性，在輸配電裝備及系統安全與新技術國家重點實驗室中進行了動模試驗，其系統接線如圖3所示。

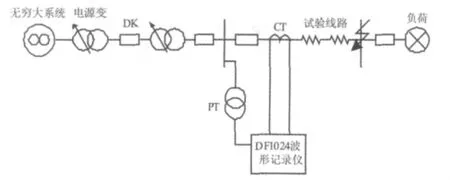
圖3 動模試驗系統

此系統中，試驗線路使用串聯阻抗器代替，所模擬的線路全長為6km，其等效參數如下:r1=0.017Ω/km，X1=0.38Ω/km，r0=0.237Ω/km，X0=1.72Ω/km。電源由 220V 無窮大系統接入，經兩組變壓器將試驗線路母線電壓調整為1000V。利用中國電力科學研究院提供的DF1024便攜式錄波儀測量PT及CT二次側電壓、電流，并將波形數據導入Matlab中進行分析計算。圖4為采樣頻率為5000Hz，線路末端發生BC相間短路時的故障錄波圖。運用本文所提出的瞬時對稱分量法提取出正、負、零序分量，結果如圖5、圖6所示。

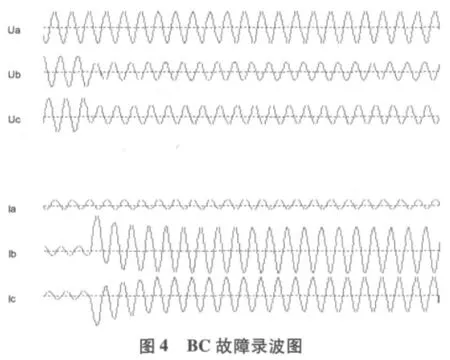
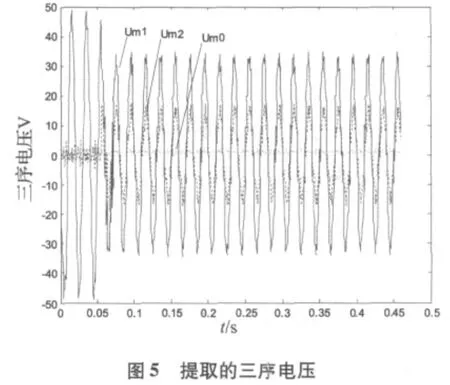
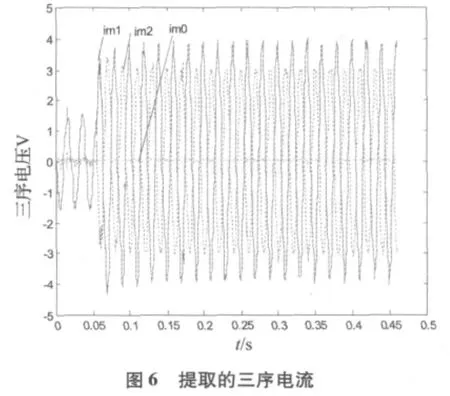
由圖5和圖6可以看出，在故障發生前，三相系統對稱，只有正序分量存在，負序和零序分量基本為零;故障發生后，零序分量仍為零，波形中僅有正序和負序分量，與BC相間短路的邊界條件一致。為進一步驗證瞬時對稱分量法的正確性，利用式(16)計算故障距離。由于故障后的衰減直流分量通常在一到兩個周波后趨于零，這在圖4中也可以看出，因此算法從故障發生一個周波后開始計算。由于方程中僅有兩個未知參數，理論上只需取兩組故障序分量值便可得到故障距離。但考慮到減小隨機誤差的影響，可選取10ms內的幾組數據進行最小二乘優化，得出較為準確的故障距離。表1給出了不同故障距離下的測距結果;表2為不同采樣頻率下試驗線路末端故障時的測距結果。表中測距誤差計算公式為

測距誤差=|測量距離－實際距離|/線路全長×100%

由表1可以看出，利用瞬時對稱分量法提取的序分量能較為準確的測量故障距離，證明了本文所提出的瞬時對稱分量法及故障暫態測距原理的正確性。由表2可以看出，隨著采樣頻率的降低，測距誤差相應增大，這是因為用差分代替求導所帶來的截斷誤差會隨采樣頻率降低而增大。

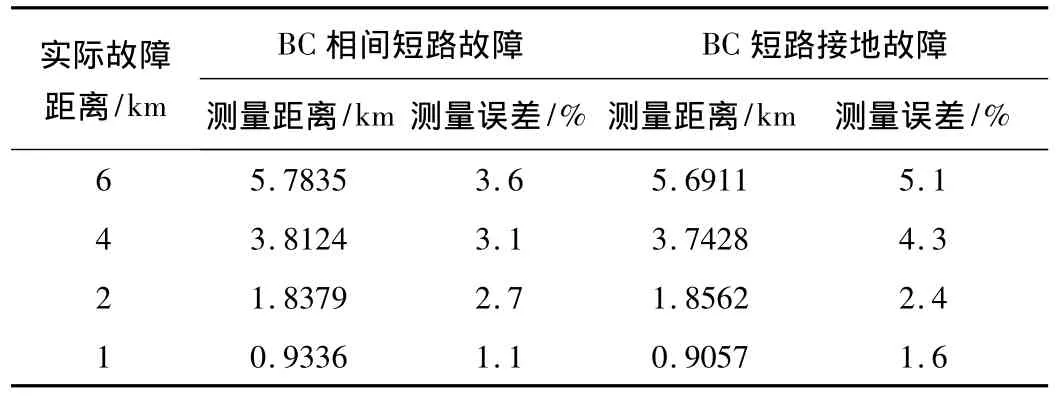
表1 不同故障距離下測距結果

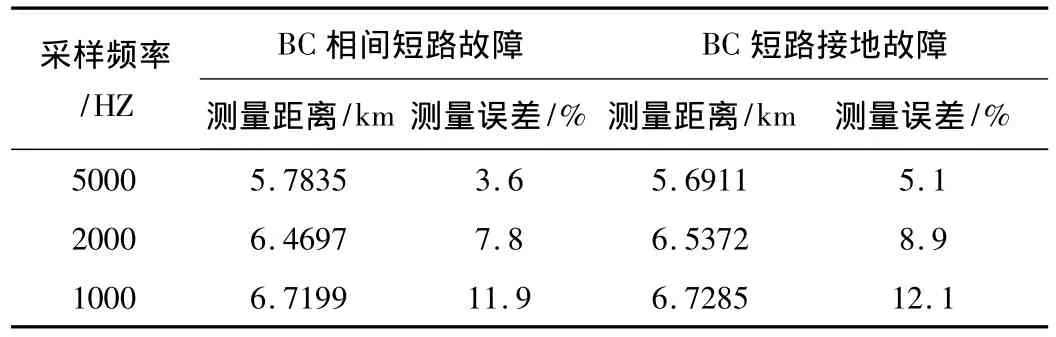
表2 不同采樣頻率測距結果

4 結論

本文提出了一種時域中在線計算序分量的瞬時對稱分量變換法，并將其應用在故障暫態測距分析中，取得了良好的試驗效果。

(1)針對傳統對稱分量變換結果為相量或復數變量，不利于電力系統實時暫態分析的缺陷，提出了基于移相操作和三角函數變換的瞬時對稱分量法，所求出的瞬時序分量不僅能夠應用于穩態分析，也能用于暫態分析。

(2)基于該理論，提出一種新型的暫態故障測距方法，思路是通過邊界條件建立故障網絡時域微分方程，將檢測點的三相電壓、電流轉換為瞬時序分量后運用最小二乘法辨識出故障距離。

(3)通過動模試驗波形分析及matlab數據計算，驗證了所提方法的正確性。隨著設備采樣頻率的提高，測距精度將得到改善。

［1］ Gerardus C.Paap.Symmetrical components in the time domain and their application to power network calculations［J］.IEEE Transactions on Power Systems，2000，15(2):522－528.

［2］ TAVARES M C，PISSOLATO J，et al.Mode Domain Multiphase Transmission Line Model-Use in Transient Studies［J］.IEEE Transactions on Power Delivery，1999，14(4):1533－1537.

［3］ 施圍，郭潔.電力系統過電壓計算［M］.北京:高等教育出版社，2006.

［4］ 諸駿偉.電力系統分析［M］.北京:水利電力出版社，1995.

［5］ Iravani MR，Karimi-Ghartemani M.Online estimation of steady state and instantaneous symmetrical components［J］.IEE Proc-Gener.Transm.Distrib，2003，150(5):616－622.

［6］ Masoud Karimi-Ghartemani，Houshang Karimi.Analysis of symmetrical components in time-domain［C］.The 48th Midwest Symposium on Circuits and Systems，Covington，Kentucky，USA，2005.

［7］ 袁旭峰，程時杰，文勁宇.改進瞬時對稱分量法及其在正負序電量檢測中的應用［J］.中國電機工程學報，2008，28(1):52－58.

［8］ 葛耀中.新型繼電保護與故障測距原理與技術［M］.西安:西安交通大學出版社，1996.

［9］ 索南加樂，齊軍，陳福鋒，等.基于R-L模型參數辨識的輸電線路準確故障測距算法［J］.中國電機工程學報，2004，24(12):119－125.

［10］ 梁振鋒，康小寧，姚李孝，等.關于故障分量概念的討論［J］.繼電器，2007，35(1):37－46.

［11］ 吳萍，張堯.基于單端電氣量的故障測距算法［J］.電力系統及其自動化學報，2003，15(4):5－7.

［12］ 束洪春，司大軍，葛耀中，等.高壓輸電線路電弧故障單端定位時域法新解［J］.中國電機工程學報，2000，20(11):25－29.

［13］ 索南加樂，劉文濤，陳勇，等.基于R-L模型誤差的自適應距離保護［J］.電力系統自動化，2006，30(22):66－72.

［14］ 王賓，董新洲，薄志謙，等.特高壓長線路單端阻抗法單相接地故障測距［J］.電力系統自動化，2008，32(14):25－29.

［15］ 方崇智，蕭德云.過程辨識［M］.北京:清華大學出版社，1998.