從高校自主招生試題看數列極限

●徐國君 (杭州外國語學校 浙江杭州 310023)

從高校自主招生試題看數列極限

●徐國君 (杭州外國語學校 浙江杭州 310023)

數列問題融計算、推理于一體，綜合性與靈活性都很強．數列問題的基礎是等差數列、等比數列，熱點是遞推(遞歸)數列(等差數列、等比數列也是一類簡單的遞推數列)．問題的形式有求值、求通項、求和以及討論數列的單調性、周期性、有界性、整除性等．而數列極限問題往往是數列綜合問題，并且是和高等數學聯系最為緊密的知識模塊之一，因而成為高校自主招生考試的重點內容之一．本文將結合高校的自主招生試題談談數列極限方面的一些淺顯見解，供同行參考．

1 高校自主招生試題中出現的數列極限的內容要點

1．1 3個最基本的極限

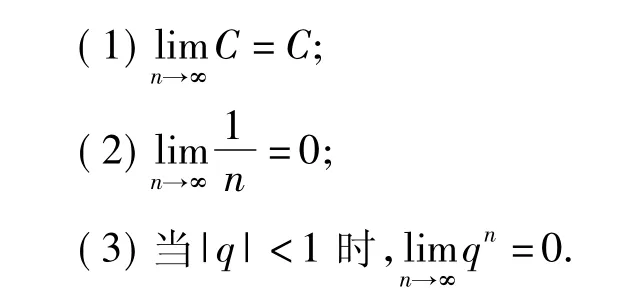
1．2 數列極限的四則運算

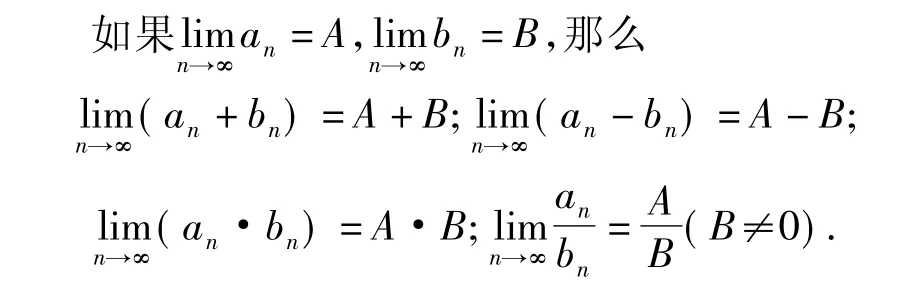
推廣上面法則可以推廣到有限多個數列的情況．例如，若{an}，{bn}，{cn}有極限，則

1．3 無窮數列各項的和

(1)無窮遞縮等比數列各項的和．

當公比|q|＜1時，無窮等比數列{an}稱為無窮遞縮等比數列．

1．4 求數列極限的方法與基本類型

(1)求數列極限的基本思路．

求和—變形—求解，而在求解前應先化為3個基本的極限形式．

(2)常見的幾類數列極限的類型和方法．

2 高校自主招生真題鏈接

分析利用n的任意性，設法消去b，先找出an－1，an與 an+1間的遞推關系式．

解(1)由條件得

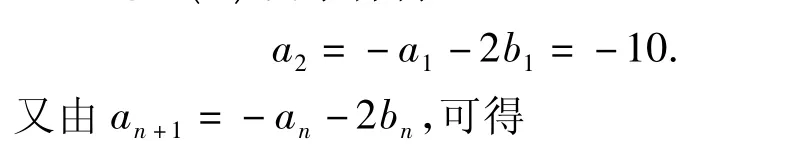
評注本題求解的關鍵是利用特征方程求數列通項的思想方法．

3 反思與認識

隨著高校自主招生的日益普及，其自主性也大大增加，近幾年還出現了高校聯盟招生，其規模日益擴大，參與的學生人數也日益增加，有著“小高考”之稱．隨著競爭的加劇，學生在準備自主招生中投入的精力也在增加．如何幫助優秀學生在準備高考之余能夠比較自如地參與高校自主招生考試，提高其成功率，是當今社會賦予我們一線教師的一項新的歷史使命．只有多鉆研、多思考、多總結才能把握高校自主招生的命題特點，有針對性地給學生進行相應的輔導和指導，才能取得事半功倍的效果．譬如數列極限內容，雖然高考基本不做要求，但是在當今自主招生中卻屢屢出現，因此，在平時教學中有必要適當滲透極限思想，并在課余時間對優秀學生適時加以指導．