對偶原理下的Menelaus定理與Ceva定理的統一

●趙臨龍 (安康學院數學系 陜西安康 725000)

對偶原理下的Menelaus定理與Ceva定理的統一

●趙臨龍 (安康學院數學系 陜西安康 725000)

在歐氏幾何中，主要研究“三點共線”與“三線共點”問題的2個重要定理:梅內勞斯(Menelaus)定理和塞瓦(Ceva)定理．而在射影幾何中，可利用對偶原理將梅內勞斯定理和塞瓦定理統一起來，充分揭示兩者的本質聯系．

1 Menelaus定理與Ceva定理

1．1 Menelaus定理

梅內勞斯作為一名古希臘的天文學家和數學家，關于圓中的弦撰寫了6本論著．這些著作和梅內勞斯的許多其他著作都失傳了．幸運的是梅內勞斯的3卷《球面幾何》以阿拉伯文保存了下來，這部著作在希臘三角學的發展中起著重要的作用．第3卷展示了當時的球面三角學，著名的梅內勞斯定理作為本書的重要基礎［1］．

命題 1(Menelaus定理)［1］一直線與△ABC的3條邊BC，CA，AB或延長線分別相交于點X，Y，Z，則

1．2 Ceva定理

塞瓦是意大利著名的經濟學家、水利專家和幾何學家，曾在重心計算法的研究上獨樹一幟，并取得了卓越的成就．他在研究各種圖形的重心性質時，同時得到了直線性質，塞瓦定理正是在他本人所著的《直線論》一書中首先發表的［1］．

命題2(Ceva定理)［1］在△ABC內任取一點O，直線 AO，BO，CO 分別交對邊于點 X，Y，Z，則

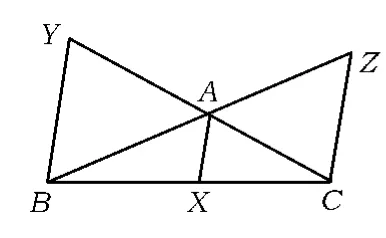
圖1

圖2

2 Menelaus定理與Ceva定理的統一

在射影幾何中，規定:平行線相交于無窮遠(如通常的太陽“平行光”就是相交于無窮遠點的“太陽”)［2］．

在射影幾何中，將一個命題的“點”換成“直線”，同時將“直線”換成“點”，并保持原有結構關系不變，所得到的新命題與原命題是“互為對偶命題”，并且2個互為對偶命題有“同真假”性質的對偶原理［2］．

這樣一來，可給出梅內勞斯定理和塞瓦定理相統一的結論——互為對偶命題．

命題3△ABC的3個頂點A，B，C與該三角形相對應的3條邊BC，CA，AB所在直線各依次有點 X，Y，Z，則點 X，Y，Z 共線的充要條件是:

命題4△ABC的3條邊BC，CA，AB所在直線與該三角形相對應的3個頂點A，B，C各依次有直線 AX，BY，CZ，則直線 AX，BY，CZ 共點的充要條件是:

3 Menelaus定理與Ceva定理的推廣

在射影幾何中，還有另外2個研究“三點共線”與“三線共點”的定理互為對偶定理．

命題5(巴斯卡(Pascal)定理［3］)一六角形ABCDEF內接于一條二次曲線Γ的充要條件是:這六邊形3雙對邊AB與DE，BC與EF，CD與FA的交點共線．

命題 6(布列安雙(Brianchon)定理［3］)一六邊形ABCDEF外切于一條二次曲線Γ的充要條件是:這六邊形3雙對角線AD，BE，CF共點．

特例(1)(命題5的退化形式)三邊形內接一條二次曲線，則其3條邊與對頂的切線的3個交點共線．

(2)(命題6的退化形式)三邊形外切一條二次曲線，則其3個頂點與對邊上的切點的3條連線共點．

3．1 定理的推廣

命題7△ABC的一條外接二次曲線Γ在三頂點 A，B，C 的切線依次是 AX，BY，CZ，則該三角形的3條邊BC，CA，AB與對頂切線3個交點X，Y，Z共線的充要條件是:

(梅內勞斯定理的推廣)

命題8△ABC的一條二次曲線Γ在3條邊BC，CA，AB 所在直線的切點依次是 X，Y，Z，則該三角形3個頂點A，B，C與對邊切點3條連線 AX，BY，CZ共點的充要條件是:

(塞瓦定理的推廣)

2個命題只需要證明其中一個即可．如圖2，對于命題8，由特例(2)，得3條連線 AX，BY，CZ共點．又由塞瓦定理，得3條連線AX，BY，CZ共點的充要條件是:

3．2 定理的變形

(1)在命題7中，當二次曲線Γ退化為圓時，是一道1989年新加坡數學競賽題;在命題8中，當二次曲線Γ為橢圓時，是《數學學習》的“數學問題與解答”欄目中的問題 799［4］．

(2)在命題7中，當二次曲線Γ退化為不在△ABC邊上的一點時，就是塞瓦定理;在命題8中，當二次曲線Γ退化為不在△ABC頂點的一直線時，就是梅內勞斯定理．

結論(2)正好反映了梅內勞斯定理和塞瓦定理的內在聯系，推廣的梅內勞斯定理的退化是塞瓦定理;推廣的塞瓦定理的退化是梅內勞斯定理．

(此文為陜西普通本科高等學校教學改革研究項目(09BY70);安康學院重點扶持學科《基礎數學》建設項目(AZXZ0107)．)

［1］ 張紅．數學簡史［M］．北京:科學出版社，2007．

［2］ 朱德祥．高等幾何［M］．北京:高等教育出版社，1983．

［3］ 趙臨龍，張小文．射影幾何中的共點線(共線點)定理的關系［J］．鞍山師范學院學報，2003(3):44-46．

［4］ 劉才華．數學問題與解答［J］．數學學習，2009(12):46-47．