借助四面體巧解異面直線所成的角

●方志平 (惠州市第一中學 廣東惠州 516007)

借助四面體巧解異面直線所成的角

●方志平 (惠州市第一中學 廣東惠州 516007)

用幾何的方法求異面直線所成的角，往往是先通過平移異面直線到相交位置，再找出異面直線所成的角，然后由三角知識求出異面直線所成角的函數值或求出角的大小．由于四面體的任何一組對棱都是異面直線，因此以四面體為載體，把異面直線放在四面體的對棱所在的位置，利用四面體對棱的夾角公式可巧解異面直線所成的角．現闡述如下:

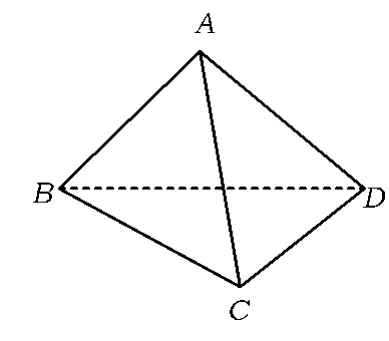
圖1

1 四面體對棱的夾角公式

如圖1，在四面體A-BCD中，若AC與BD所成的角為90°，則

2 夾角公式的應用

例1在正四面體的側面三角形的高線中，其“垂足”不在同一側面上的任意2條所成角的余弦值是 ( )

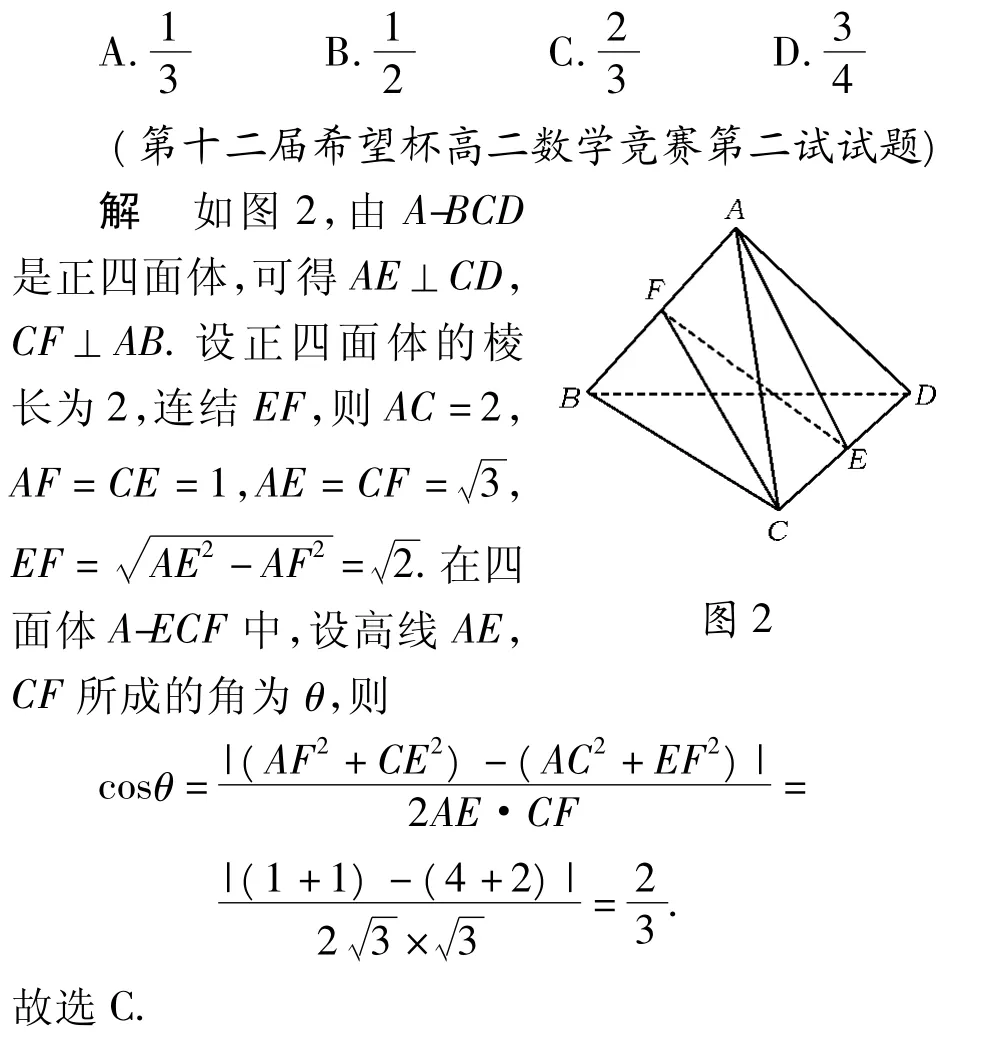
評注本題求解的關鍵是要把AE，CF放在一個棱長都易求的四面體的一組對棱上，不難發現連結EF，得AECF正是我們尋找的一個四面體．

評注雖然圖3中的CA1與C1B是正三棱柱2個側面的對角線，但連結A1B后，CA1和C1B卻是四面體A1BC1C的一組對棱，且四面體A1BC1C所有棱長均可求，故用四面體對棱的夾角公式可求異面直線CA1與C1B所成角的大小．

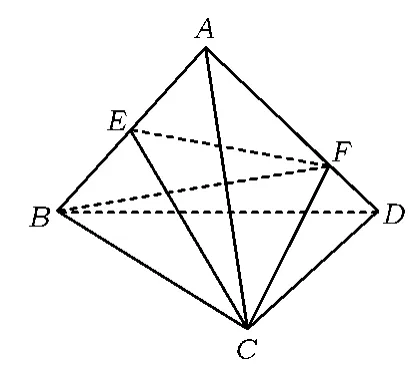
圖4

(2008年福建省福州市第30屆高中數學競賽試題)

解如圖4，連結 EF，CF．設正四面體 ABCD棱長為6，在△AEF中，

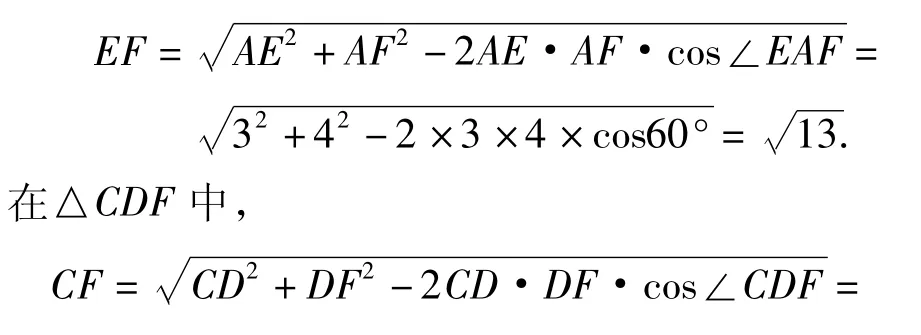
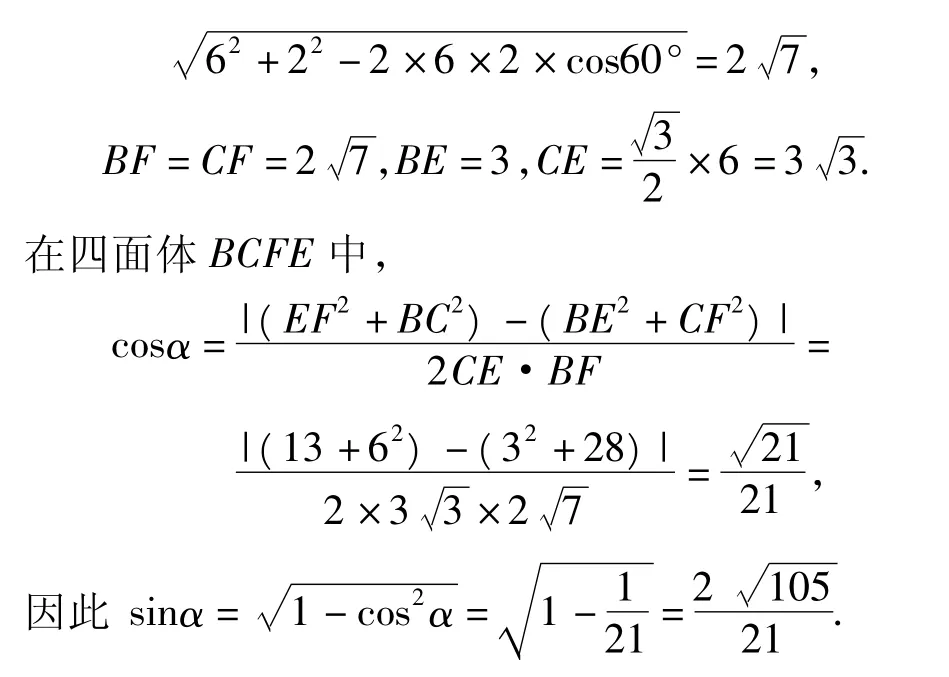
評注本題求解的關鍵是要構造一個使得CE與BF成為四面體的一組對棱，且該四面體所有棱均可求．顯然連結EF，CF可得一個四面體BCFE符合要求，然后借助四面體對棱的夾角公式可求異面直線CE與BF所成角的余弦值，進而求出該角的正弦值．

綜上所述，對于任何一對異面直線，以四面體為載體，只要能恰當地把這對異面直線放在一個四面體的一組對棱的位置，且該四面體所有棱長均可求，這樣就能巧解這對異面直線所成角的問題．