2011年中考模擬測試題(2)

445500 黃梅縣晉梅中學 洪建明

2011年中考模擬測試題(2)

445500 黃梅縣晉梅中學 洪建明

一、填空題(3分×10=30分)

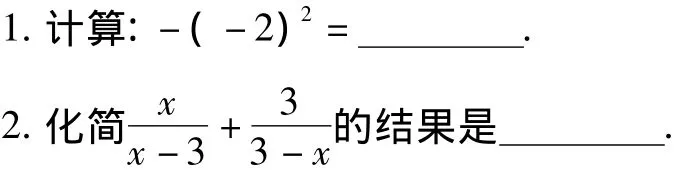
3.“太陽能”是一種既無污染又節省地下能源的能量，據相關資料介紹，平均每平方千米的地面一年從太陽中獲得的能量，相當于燃燒130000000千克的煤所產生的能量，用科學記數法表示這個數是＿＿千克.

4.已知點 A(m －1，3)與點 B(2，n+1)關于 x軸對稱，則點 P(m，n)的坐標為＿＿.

7.⊙O1與⊙O2的圓心距為5，⊙O1的半徑為 3，若兩圓相切，則⊙O2的半徑為＿＿或＿＿.

8.把一個半徑為8cm的圓片，剪掉一個圓心角為90°的扇形后，用剩下的部分做成一個圓錐的側面，則這個圓錐的高為＿＿cm.

9.如圖是長方形時鐘鐘面示意圖，長方形上下的寬為40厘米，時鐘的中心在長方形對角線的交點上，數字2在長方形的頂點上，數字3，6，9，12標在所在邊的中點上，則長方形左右的長應為＿＿厘米.

10.將半徑為4cm的半圓圍成一個圓錐，在圓錐內接一個圓柱(如圖示)，當圓柱的側面的面積最大時，圓柱的底面半徑是＿＿cm.

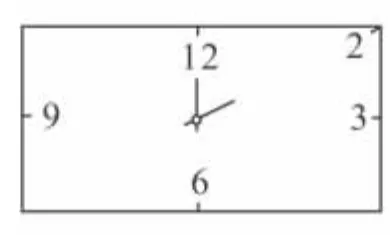
第9題圖

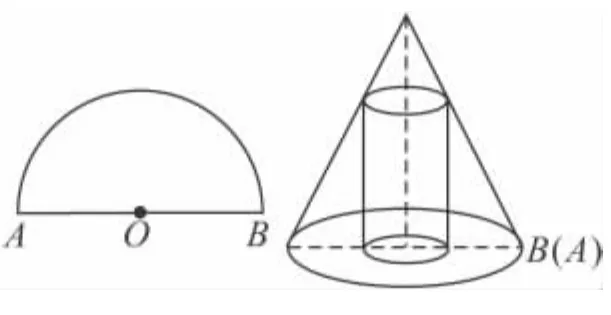
第10題圖

二、選擇題(6×3分=18分)

11.8的立方根為

A.2 B.±2

C.4 D.±4

12.下列運算正確的是

A.2a+3b=5ab B.a6÷a2=a3

C.(a+b)2=a2+b2D.a3·a2=a5

A.圖象必經過點(1，2)B.y隨x的增大而減少

C.圖象在第一、三象限內D.若 x＞1，則 y＜2;

14.如圖是一個無蓋正方體盒子的表面展開圖，A，B，C為圖上三點，則在正方體盒子中，∠ABC的度數為

A.150° B.120°C.90°D.60°

15.如圖，過邊長為1的等邊△ABC的邊AB上一點P，作PE⊥AC于E，Q為BC延長線上一點，當PA=CQ時，連PQ交AC邊于D，則DE的長為

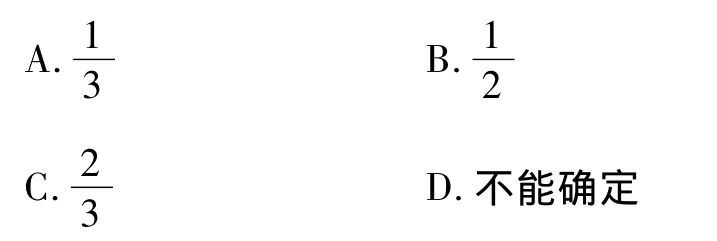
第14題圖

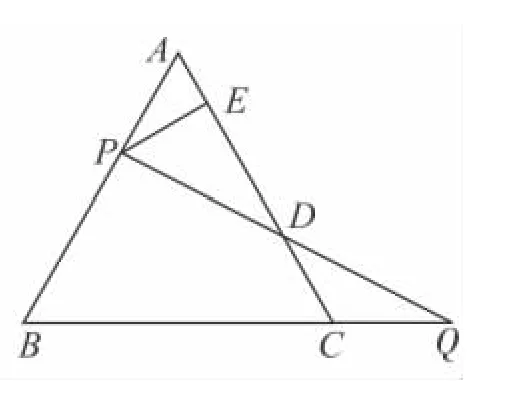
第15題圖

16.如圖，在直角梯形 ABCD中，AD∥BC，∠B=90°，E 為 AB 上一點，且ED平分∠ADC，EC平分∠BCD，

則下列結論中不正確的是

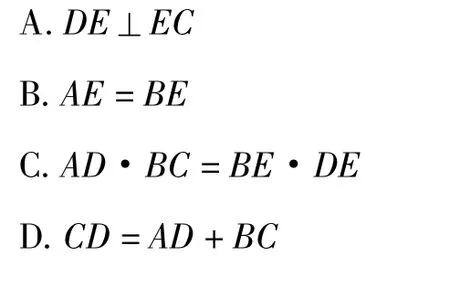
三、解答題(共9道大題，共72分)

18.(6分)如圖，已知，在?ABCD中，AE=CF，M，N 分別是 DE，BF的中點.

求證:四邊形MFNE是平行四邊形.

19.(6分)如圖是我市某校八年級學生為玉樹災區捐款情況抽樣調查的條形圖和扇形統計圖.

(1)求該樣本的容量;

(2)在扇形統計圖中，求該樣本中捐款15元的人數所占的圓心角度數;

(3)若該校八年級學生有800人，據此樣本求八年級

捐款總數.

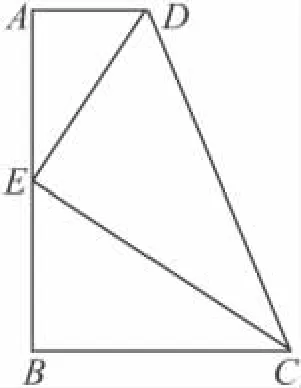
20.(4分 ×2=8分)如圖，已知⊙O的弦AB垂直于直徑CD，垂足為 F，點 E在 AB上，且 EA=EC.

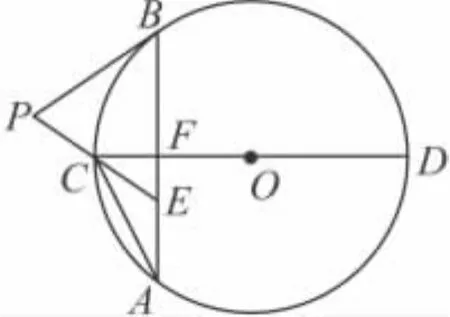
(1)求證:AC2=AE·AB;

(2)延長EC到點P，連結PB，若PB=PE，試判斷PB與⊙O的位置關系，并說明理由.

21.(8分)如圖，某天然氣公司的主輸氣管道從A市的東偏北30°方向直線延伸，測繪員在A處測得要安裝天然氣的M小區在A市東偏北60°方向，測繪員沿主輸氣管道步行2000米到達C處，測得小區M位于C的北偏西60°方向，請你在主輸氣管道上尋找支管道連接點N，使到該小區鋪設的管道最短，并求AN的長.

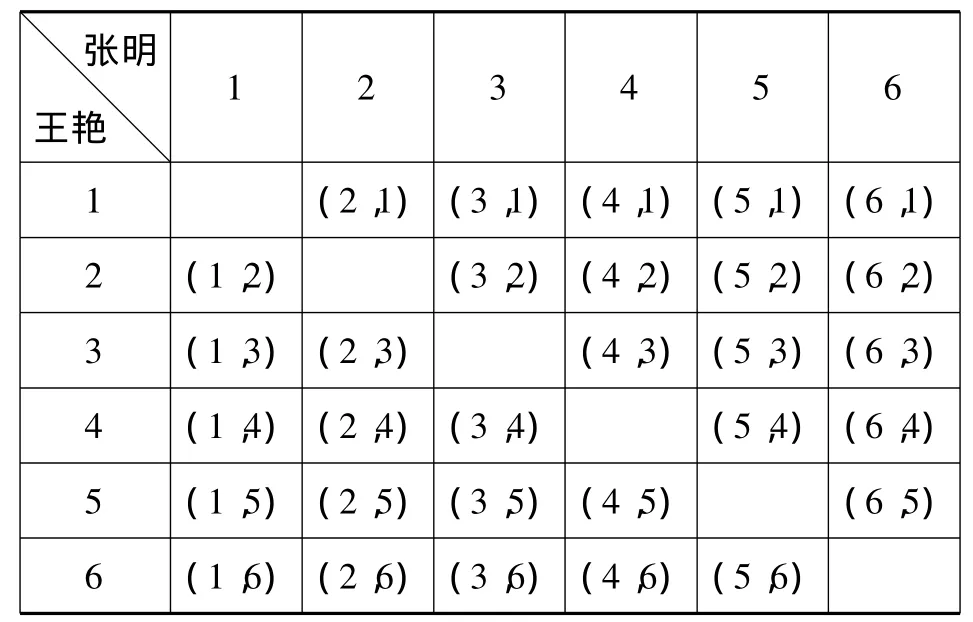
22.(6分)暑假快到了，老家在十堰的大學生張明與王艷打算留在上海，為世博會做義工.學校爭取到6個義工名額，分別安排在中國館園區3個名額，世博軸園區2個名額，演義中心園區1個名額.學校把分別標號為 1，2，3，4，5，6 的六個質地大小均相同的小球，放在不透明的袋子里，并規定標號1，2，3的到中國館，標號4，5到世博軸，標號6的到演藝中心，讓張明、王艷各摸1個.

(1)求張明到中國館做義工的概率;

(2)求張明、王艷各自在世博軸、演藝中心做義工的概率.

23.(8分)某學校組織八年級學生參加社會實踐活動，若單獨租用35座客車若干輛，則剛好坐滿;若單獨租用55座客車，則可以少租一輛，且余45個空座位.(1)求該校八年級學生參加社會實踐活動的人數;(2)已知35座客車的租金為每輛320元，55座客車的租金為每輛400元.根據租車資金不超過1500元的預算，學校決定同時租用這兩種客車共4輛(可以坐不滿).請你計算本次社會實踐活動所需車輛的租金.

24.(12分)我市高新技術開發區的某公司，用480萬元購得某種產品的生產技術后，并進一步投入資金1520萬元購買生產設備，進行該產品的生產加工，已知生產這種產品每件還需成本費40元.經過市場調研發現:該產品的銷售單價，需定在100元到300元之間較為合理.當銷售單價定為100元時，年銷售量為20萬件;當銷售單價超過100元，但不超過200元時，每件新產品的銷售價格每增加10元，年銷售量將減少0.8萬件;當銷售單價超過200元，但不超過300元時，每件產品的銷售價格每增加10元，年銷售量將減少1萬件.設銷售單價為x(元)，年銷售量為y(萬件)，年獲利為w(萬元).(年獲利=年銷售額－生產成本－投資成本)

(1)求y與x之間的函數關系式;

(2)求第一年的年獲利w與x間的函數關系式，并說明投資的第一年，該公司是盈利還是虧損?若盈利，最大利潤是多少?若虧損，最少虧損是多少?

(3)若該公司希望到第二年底，除去第一年的最大盈利(或最小虧損)后，兩年的總盈利不低于1842萬元，請你確定此時銷售單價的范圍.在此情況下，要使產品銷售量最大，銷售單價應定為多少元?

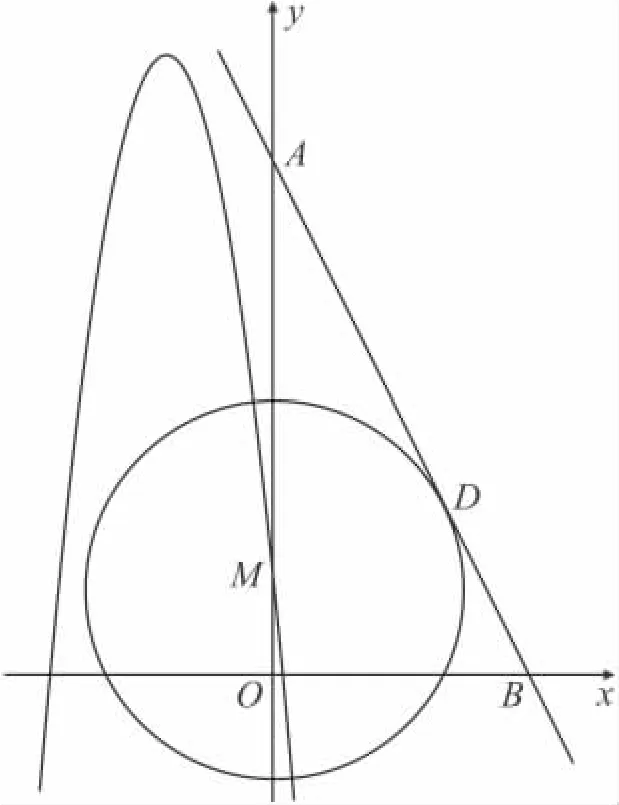
25.(12分)如圖，已知直線y=－2x+12分別與y軸，x軸交于A，B兩點，點M在y軸上，以點M為圓心的⊙M與直線AB相切于點D，連接MD.(12分)

(1)求證:△ADM∽△AOB;

(3)在(2)的條件下，試問此拋物線上是否存在點P，使得以P，A，M為頂點的三角形與△AOB相似?如果存在，請求出所有符合條件的點P的坐標;如果不存在，請說明理由.

參考答案

一、填空題

1.－4 2.1 3.1.3 ×1084.(3，－4)

5.x≤0.5 且 x≠ －3

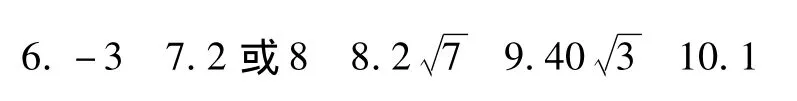
二、選擇題

11.A 12.D 13.B 14.D 15.B 16.C

三、解答題

17.由①得 x≤2，由②得 x＞1.5，∴ 1.5 ＜ x≤2.

18.提示:先證明 BE∥DF，得?BEDF，得 DE∥BF，再證明ME∥FN，得?MFNE.

19.(1)15÷30%=50(人).

(2)20% ×360°=72°.

(3)(5×15+10×25+15×10)÷50×800=7600元.

20.提示:(1)連接BC，證明△ACE∽△ABC即可得到;

(2)連接OB，證明OB⊥PB即可.

21.過 M 作 MN⊥AC，可求出∠MAN=30°，∠ANM=90°，∠ACM=60°，

此時MN最小，AN=1500米.

張明王艷1 2 3 4 5 6 1(2，1)(3，1)(4，1)(5，1)(6，1)2 (1，2) (3，2)(4，2)(5，2)(6，2)3 (1，3)(2，3) (4，3)(5，3)(6，3)4 (1，4)(2，4)(3，4) (5，4)(6，4)5 (1，5)(2，5)(3，5)(4，5) (6，5)6 (1，6)(2，6)(3，6)(4，6)(5，6)

23.(1)設單獨租用35座客車需x輛，由題意得

35x=55(x－1)－45，解得 x=5.

∴ 35x=35×5=175(人).

答:該校八年級參加社會實踐活動的人數為175人.

(2)設租35座客車y輛，則租55座客車(4－y)輛，

由題意得

∵y取正整數，∴y=2.

∴ 4－y=4－2=2.

∴ 320×2+400×2=1440(元).

所以本次社會實踐活動所需車輛的租金為1440元.

24.(1)①當100≤x≤200時，

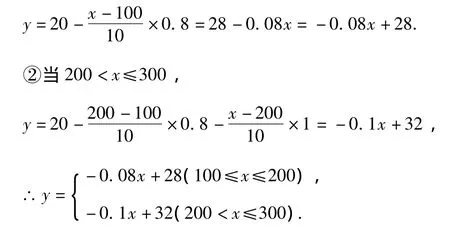
(2)投資總成本為480+1520=2000萬元，而w=(x－40)y－2000，

①當100≤x≤200 時，y= －0.08x+28，

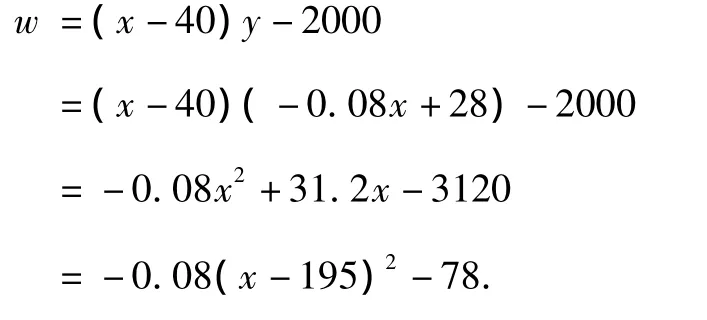
可見第一年在100≤x≤200注定虧損，

當x=195時虧損最少，為w最大值=－78萬元.

②當200＜x≤300時，y= －0.1x+32，

可見第一年在200＜x≤300注定虧損，x＞200時虧損最少，w最大值＜ －80萬元.

綜上可見，x=195時虧損最少，為虧損78萬元.

(3)兩年的總盈利不低于1842元，可見第二年至少要盈利1842+78=1920萬元，既然兩年一塊算，第二年我們就不用算投資成本那2000萬元了.

第二年:

解不等式得到:190≤x≤200.

解不等式得160≤x≤200，聯合200≤x≤300，也就只有x=200.

綜上有190≤x≤200為解.

這時候再看 y= －0.08x+28，可見 x=190時，y最大，為 12.8，

所以定價190元時候，銷售量最大.

25.(1)連接 OD，證明略;

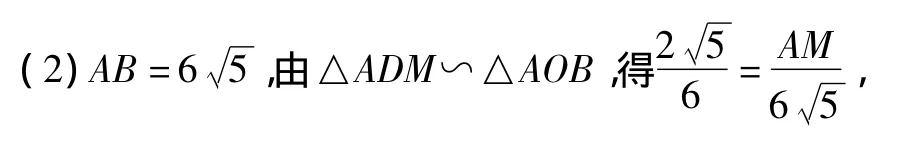
解得AM=10得OM=2，

∴ M(0，2).

設 y=a(x+2.5)2+14.5，把 M(0，2)代入得 a= －2，∴ y= －2(x－2.5)2+14.5= －2x2－10x+2.

(3)①若△AMP∽△ADM，則得∠AMP=90°，則PM∥x軸，故 －2x2－10x+2=2得 x1=0(舍)，x2= －5，

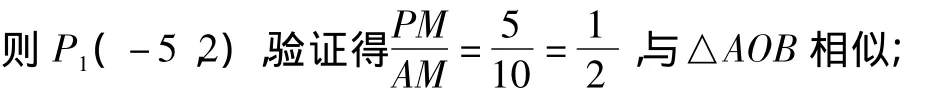
②若AM為斜邊，若△PAM與△AOB相似，而△AOB與△AMD相似，故△ADM≌△APM，

先求得xD=4，∴xP2=－4，代入得yP2

=10，

即 P2(－4，10)，

20110524)