地板磚引發的勾股定理萬能證明
430079 武漢華中師范大學國家數字化學習工程技術研究中心 彭翕成 張景中
地板磚引發的勾股定理萬能證明
430079 武漢華中師范大學國家數字化學習工程技術研究中心 彭翕成 張景中
筆者曾經撰文介紹如何用兩個三角形拼擺,得出了勾股定理的多種證法.當然,我們也可以利用計算機,給出勾股定理的多種證法.這種設計來自畢達哥拉斯的啟發.
在西方,勾股定理又被稱為畢達哥拉斯定理.相傳,古希臘數學家畢達哥拉斯是在觀察地板圖案時發現了勾股定理.由于地板圖案都是一樣大小的正方形,所以畢達哥拉斯最先發現的是勾股定理對于等腰直角三角形成立(圖1).
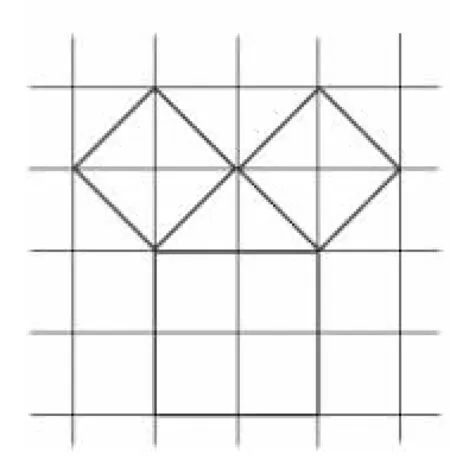
圖1
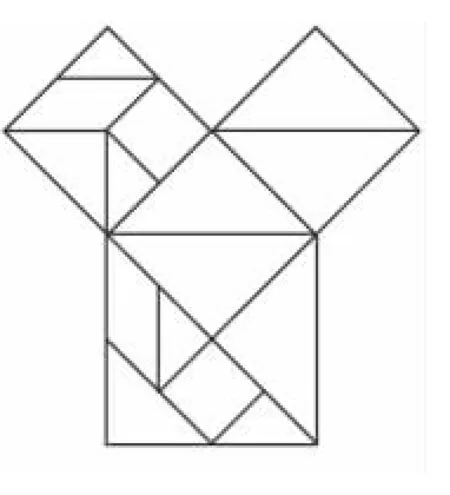
圖2
十分巧合的是,我國古代也有類似的圖形(圖2).不過這個圖形不是從地板圖案而來,而是將一個正方形紙板分成7份,然后重新進行組合.這算是益智游戲七巧板的一個應用吧.
設計一種地板圖案如圖3所示,您能從中發現勾股定理么?您若一眼就能看出該圖蘊含了勾股定理的三種證法,那就恭喜您有不錯的幾何直覺!
其實,圖中的奧妙遠不局限于此.假如設計一種由一大一小正方形鋪成的地板,然后我們拿一個正方形紙板(其邊長的平方等于原來兩個正方形的邊長平方和)隨手往上一扔,一扔就得到一種證法.扔到特殊位置,面積分割起來就比較簡單一點;而扔到一般位置,面積分割起來就需要多一些功夫.
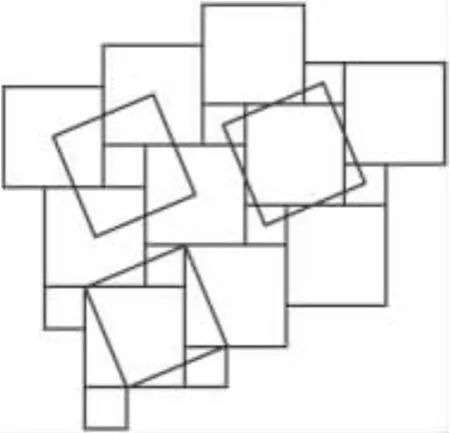
圖3
為了更清楚地說明,我們用動態幾何軟件——超級畫板制作了一個課件《勾股定理的萬能證明.zjz》.此課件使用很簡單,只要拖動屏幕上兩個點,就能批量產生勾股定理面積分割證明.大家有興趣的話,可以到網上去下載,只需在百度上搜索“勾股定理的萬能證明”即可.該課件用超級畫板打開.
打開課件后,出現界面如圖4所示,這本身就是一種證明.為了讓演示有序進行,我們先保持紅點不變,拖動黃色點,使之從左上方頂點開始,逆時針繞一圈(圖5~圖16).
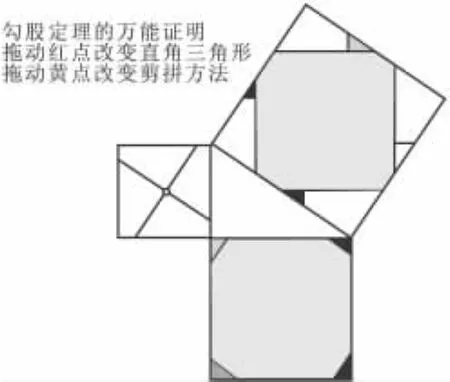
圖4
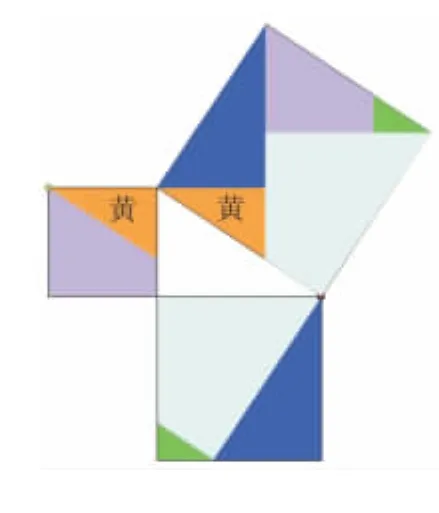
圖5(5塊)
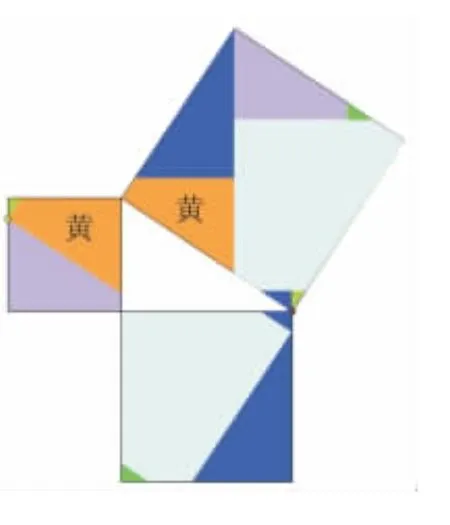
圖6(7塊)
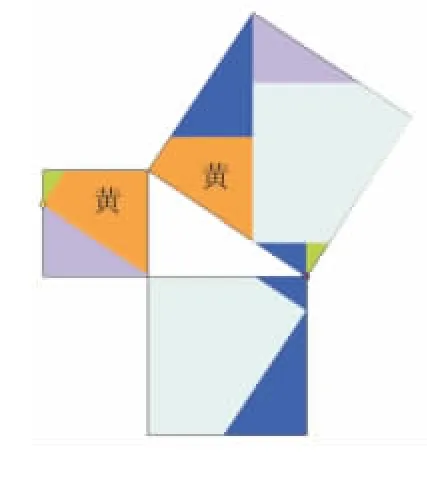
圖7(6塊)

圖8(5塊)

圖9(7塊)
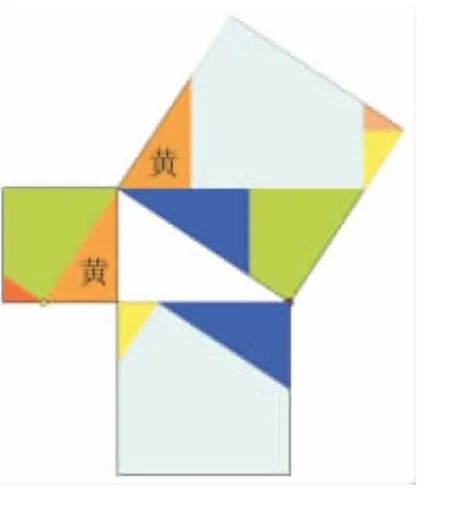
圖10(6塊)

圖11(5塊)
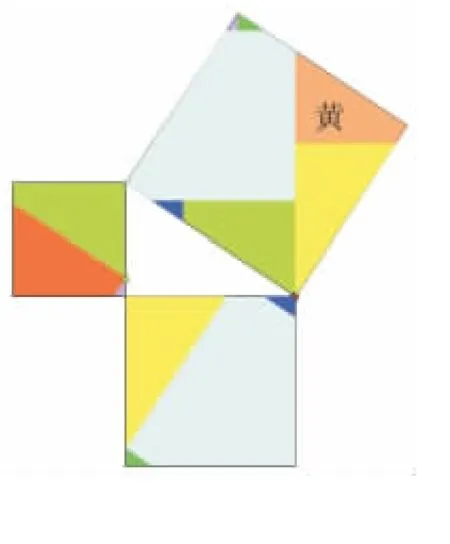
圖12(7塊)
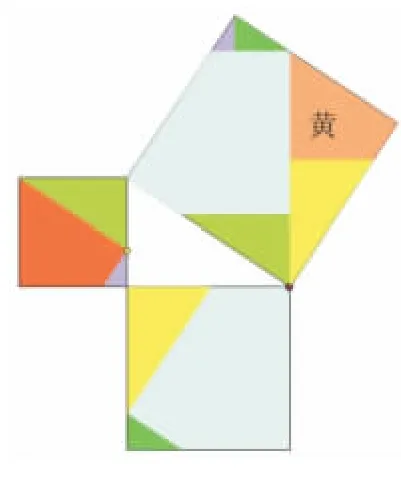
圖13(6塊)
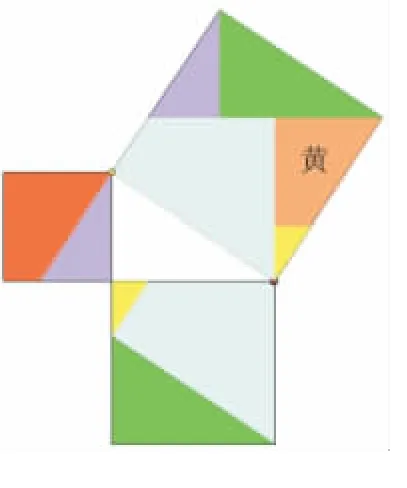
圖14(5塊)
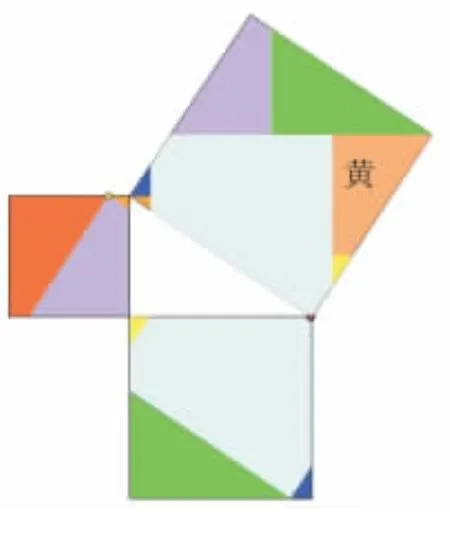
圖15(7塊)

圖16(6塊)
黃色點在周界上繞完一周后.我們拖動它從左上頂點出發,在內部緩慢移動(圖17~圖18).
拖動黃色點調整三角形形狀,此時黃色點在直角邊上較大正方形內.我們仍然從左上方頂點開始拖動黃色點(圖19~圖21).
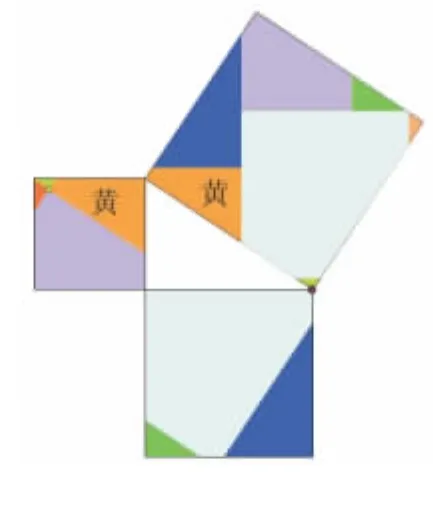
圖17(7塊)
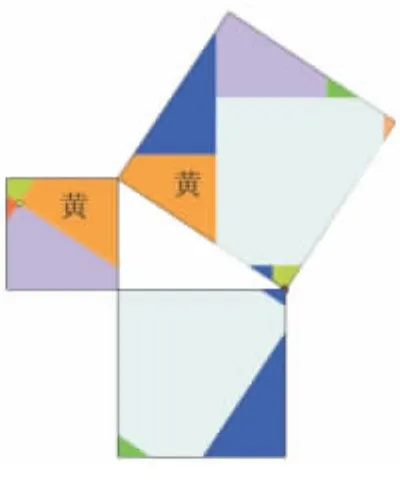
圖18(8塊)
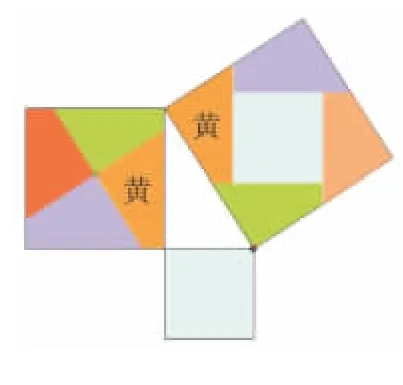
圖19(5塊)
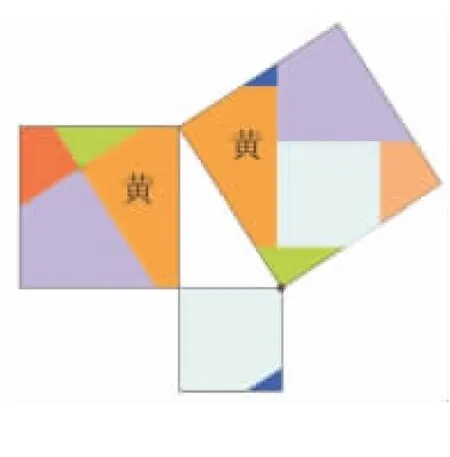
圖20(6塊)

圖21(6塊)
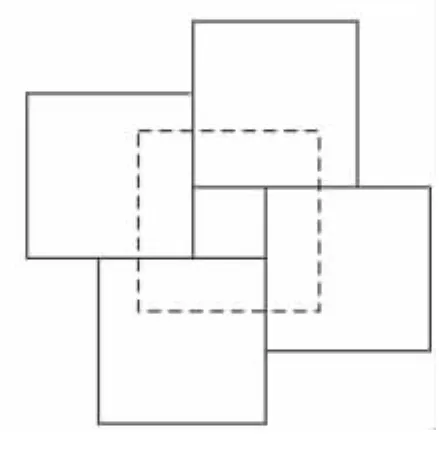
圖22(6塊)
以上只是截取的部分圖片,只要有時間,可以得到更多的證明.稱之為萬能證明,一點都不為過.
以上的變化,都是斜邊上的正方形平移作分割.如果考慮旋轉則復雜很多,譬如圖22的情形可不大容易看出來,還得進一步分割.
勾股定理的證明已經足夠多了.多幾種、少幾種,影響并不大.但利用計算機軟件批量生成證明,則是一件很有趣的事情,這也是過去難以想象的.采用先進的技術手段,用探索發現的心態去研究數學,能夠看到更多的精彩.
另外,我們也不能忘記是古老的傳說故事給予我們的啟發,踩在腳下的地板磚看似地位卑微,但卻充滿智慧.它能給我們靈感,解答我們心中的疑惑.譬如拿破侖定理,從任意三角形三邊出發向外作三個等邊三角形,而這三個等邊三角形的中心構成一個新的等邊三角形.這是難倒很多數學愛好者的經典問題.讓地板磚來告訴我們怎么做吧.
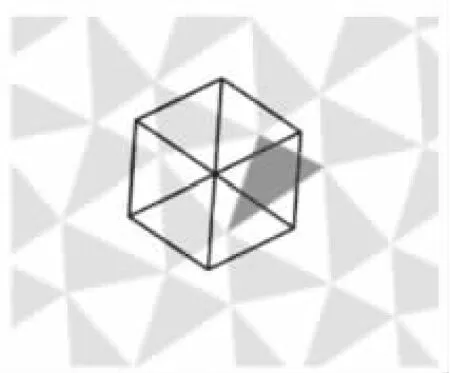
圖23
如圖23,假定黑色三角形是最初的任意三角形,以其中一邊向外作好等邊三角形,再以該等邊三角形的中心為旋轉中心,將原三角形分別旋轉120°和240°,然后以三個非等邊三角形向外作等邊三角形.這樣的操作是可以持續做下去的,直到鋪滿整個平面.而若我們連接其中的幾個中心,就能構造出一個正六邊形.這也就得到了拿破侖定理的一個無字證明.
這又給我們啟發,單獨看某個事物,可能難以看出什么門道.而若將其放之特定環境,從整體來看,很可能就能發現內藏的規律.
20110601)

