遷移解法再探究 拓廣演變提能力

221700 江蘇省豐縣黃樓初級中學 王慶志

遷移解法再探究 拓廣演變提能力

221700 江蘇省豐縣黃樓初級中學 王慶志

以課本中的典型習題為素材由淺入深，由此及彼地努力探索問題的衍生點，通過變換命題的條件與結論，或通過創(chuàng)設新的問題情境進行“深加工”，類比遷移、延伸拓展，進行創(chuàng)造性的改編可以演變出許多的新問題，通過解題與聯(lián)想把蘊涵其中的數(shù)學思想方法揭示出來，挖掘出隱含的問題的本質(zhì)屬性，對于提高同學們探索創(chuàng)新能力、解題的思維技能有著重要的作用.本文以九年級《數(shù)學》(義務教育課程標準實驗教科書(江蘇科學技術出版社)上冊第137頁第13題)習題為例闡釋如下.

1 原題及解法

題目 如圖1，在 Rt△ABC中，∠C=90°，它的內(nèi)切⊙O 分別與邊AB，BC，CA相切于點D，E，F(xiàn)，且 BD=6，AD=4，求⊙O的半徑r.

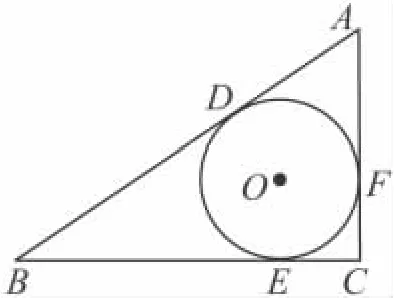
圖1

解法1 根據(jù)直角三角形的勾股定理構造關于內(nèi)切圓半徑的一元二次方程求解.

連接OE，OF，根據(jù)“切線垂直于過切點的半徑”可知 OE⊥BC，OF⊥AC，

又∠ACB=90°，所以四邊形OECF是矩形，又OE=OF，所以四邊形OECF是正方形，

設⊙O的半徑為r，則CE=CF=r，

根據(jù)“從圓外一點引圓的兩條切線，它們的切線長相等”，

所以 AF=AD=4，BE=BD=6，

在Rt△ABC中由勾股定理得AC2+BC2=AB2，

即(4+r)2+(6+r)2=(4+6)2，

解之得r=2，r=－12(不合題意，舍去)

所以⊙O的半徑為2.

解法2 根據(jù)直角三角形的面積構造關于內(nèi)切圓半徑的一元二次方程求解.

連接OA，OB，OC將Rt△ABC分成3個三角形，分別為△OAB，△OBC，△OCA它們的高都是內(nèi)切圓的半徑，根據(jù)整體等于部分之和(設r為內(nèi)切圓的半徑)可得

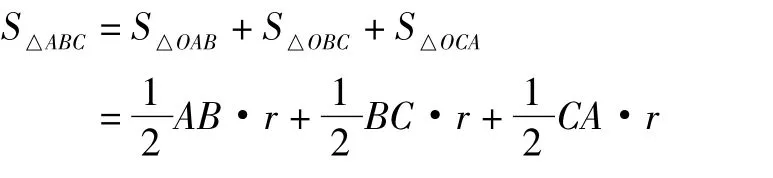
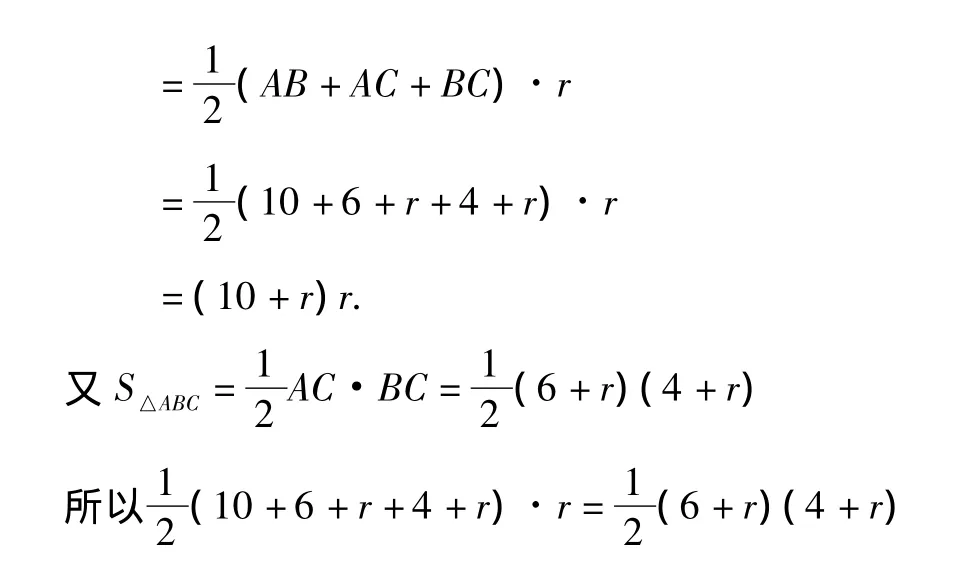
解之，得r=2，r=－12(不合題意，舍去)

所以⊙O的半徑為2.

2 反思解題過程，探究拓展問題

初中學生的年齡特征及數(shù)學認知結構水平，決定了他(她)們往往只熱衷于做習題，卻不對解題思路進行反思、總結，這樣的解題只停留在經(jīng)驗水平上，往往事倍功半.在學生解決每一個數(shù)學問題之后，引導學生對解題過程進行自我反思總結，可以觸及學生元認知思維水平的需要，提升從感性認識到理性認識的飛躍.學之道在于“悟”，只有通過反思，學生的思維才能真正啟動，思想才能得到升華.

從解法2的探究過程中，可以發(fā)現(xiàn)其中隱含了一種重要的數(shù)學解題思維方法——有些圖形的面積可以通過適當?shù)姆指睿谜w等于各個部分面積之和(“同一個圖形分割后整體的面積等于各個部分之和”)來獲得一種行之有效的解決問題的策略.

拓展1 直角三角形是特殊的三角形，又是多邊形中最簡單的一種圖形，任意的三角形都存在唯一的內(nèi)切圓，但四邊形不一定存在內(nèi)切圓，假若四邊形存在一個內(nèi)切圓上述結論成立嗎?對于任意的n邊形呢?

例1 閱讀材料:如圖2，△ABC的周長為 l，內(nèi)切圓O的半徑為 r，連接 OA，OB，OC，△ABC被劃分為三個小三角形，用 S△ABC表示△ABC 的面積.

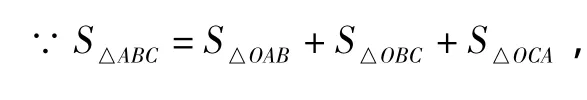
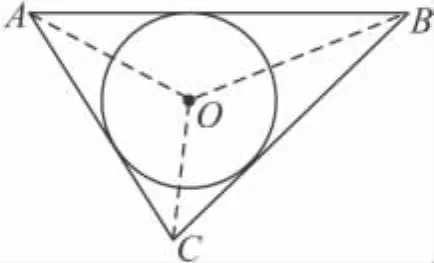
圖2

(1)理解與應用:利用公式計算邊長分別為5，12，13的三角形內(nèi)切圓半徑;

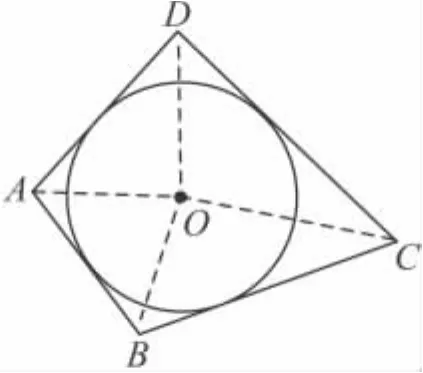
圖3

(2)類比與推理:若四邊形ABCD存在內(nèi)切圓(與各邊都相切的圓)如圖3，且面積為 S，各邊長分別為 a，b，c，d，試推導四邊形的內(nèi)切圓半徑公式;

(3)拓展與延伸:若一個n邊形(n為不小于3的整數(shù))存在內(nèi)切圓，且面積為S，各邊長分別為 a1，a2，a3，…，an，合理猜想其內(nèi)切圓半徑公式(不需說明理由).

解析 本題創(chuàng)設了一個以“閱讀材料—三角形的面積與內(nèi)切圓半徑及周長之間關系”的問題背景，其中的巧妙之處在于分割后3個三角形的高均為內(nèi)切圓的半徑，因而三角形的面積等于三角形的周長之半與內(nèi)切圓半徑之積.

(1)首先根據(jù)三邊之間關系判定是直角三角形，即52+122=132由勾股定理的逆定理可知:邊長分別為5，12，13 的三角形，所以 S=×5×12=30，設內(nèi)切圓

△ABC半徑為r，則有30=(5+12+13)·r，所以 r=2.

(2)設四邊形內(nèi)切圓的圓心為點O，分別連接OA，OB，OC，OD，將四邊形ABCD分割為4個三角形△AOB，△BOC，△COD，△DOA，它們的高視為四邊形 ABCD的內(nèi)切圓半徑，則有S=(a+b+c+d)·r，所以 r=

(3)根據(jù)閱讀材料及問題(2)的解答過程，進行類比推理，不難猜想:面積為 S，各邊長分別為 a1，a2，a3，…，an的n邊形(n為不小于3的整數(shù))內(nèi)切圓半徑公式

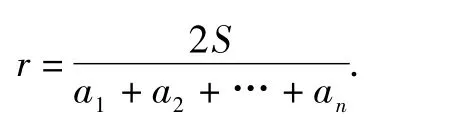
點評 本題提供的是“一個多邊形如果存在內(nèi)切圓，那么這個多邊形的面積如何用多邊形的周長及內(nèi)切圓的半徑來表示”的研究課題，試題首先從最簡單三角形的內(nèi)切圓入手讓學生通過閱讀獲得問題的解題方法，經(jīng)歷解決問題的過程并掌握得到問題的結論，然后讓學生用類比遷移問題的處理方法，去解決四邊形內(nèi)切圓問題，然后從特殊到一般讓學生猜想對任意的n邊形的內(nèi)切圓的半徑與n邊形的面積與各邊長之間的關系.通過本題的解答讀者應該掌握“學會從‘特殊情況、簡單情況’入手，觀察分析推理，得出規(guī)律后再向‘一般情況’推廣的研究問題”的數(shù)學方法.

拓展2 例2 已知Rt△ABC 中，∠ACB=90°，AC=6，BC=8.

(1)如圖4，若半徑為r1的⊙O是 Rt△ABC的內(nèi)切圓，求r1;

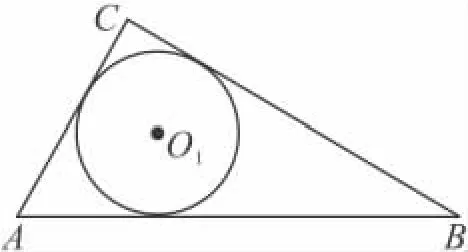
圖4

(2)如圖5，若半徑為 r2的兩個等圓⊙O1，⊙O2外切，且⊙O1與 AC，AB 相切，⊙O2與 BC，AB 相切，求 r2;

(3)如圖6，當n是大于2的正整數(shù)時，若半徑為rn的n個等圓⊙O1，⊙O2，…，⊙On依次外切，且⊙O1與AC，AB 相切，⊙On與 BC，AB 相切，⊙O2，⊙O3，…，⊙On－1均與AB邊相切，求rn.

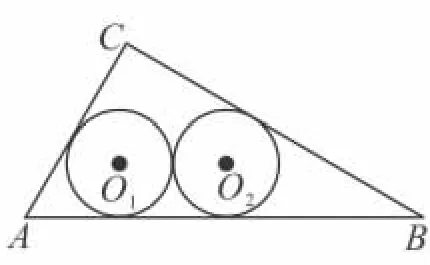
圖5

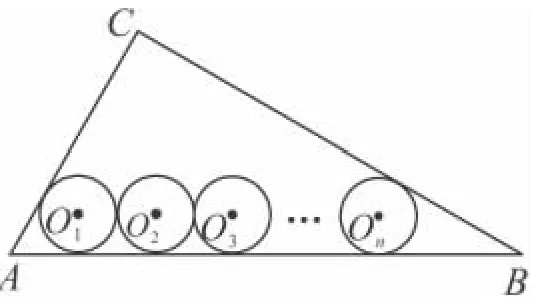
圖6

解 (1)∵ 在 Rt△ABC 中，∠ACB=90°，AC=6，BC=8.∴ AB==10.

如 圖 7，設 ⊙O1與Rt△ABC的邊 AB，BC，CA 分別切于點 D，E，F(xiàn)，連接 O1D，O1E，O1F，AO1，BO1，CO1.于是，O1D⊥AB，O1E⊥BC，O1F⊥AC，

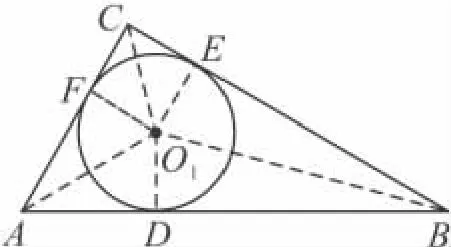
圖7

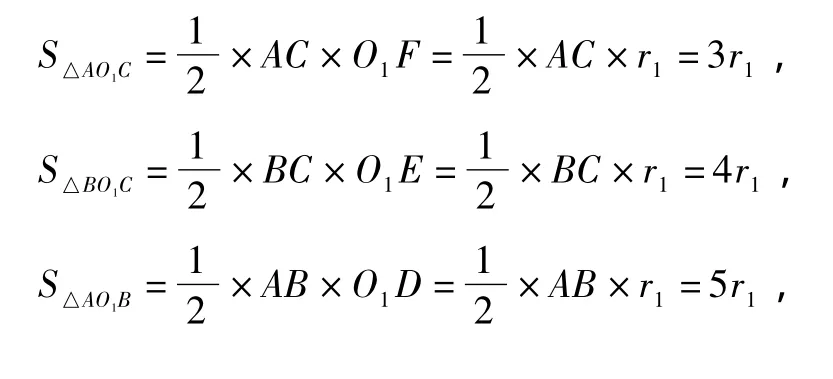
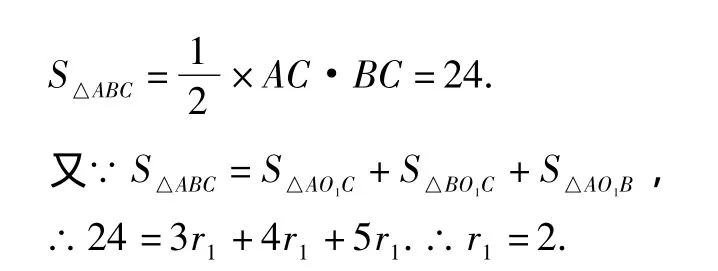
(2)如圖8連接AO1，BO2，CO1，CO2，O1O2，則

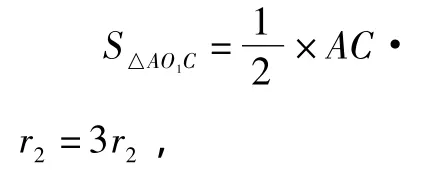
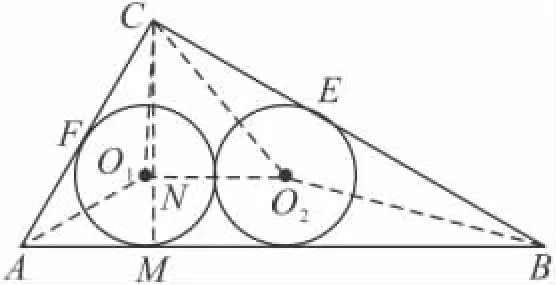
圖8

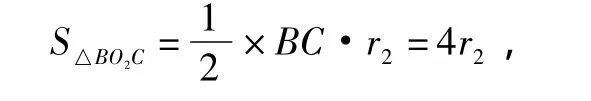
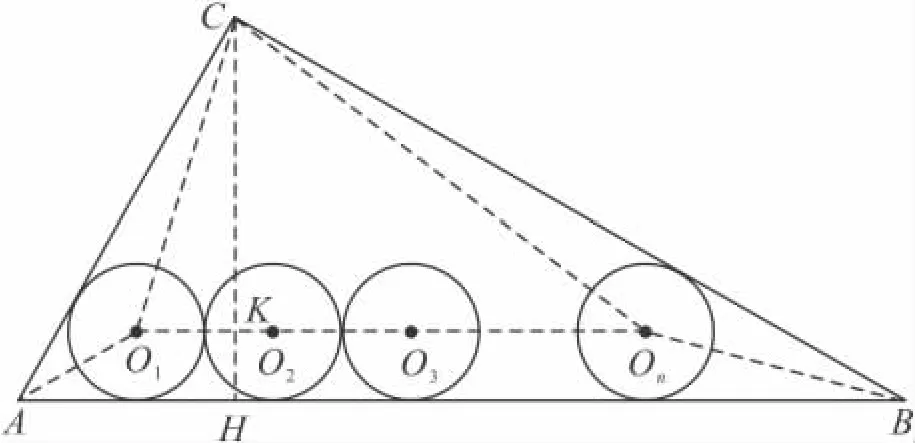
圖9

(3)如圖 9，連接 AO1，BOn，CO1，COn，O1On，

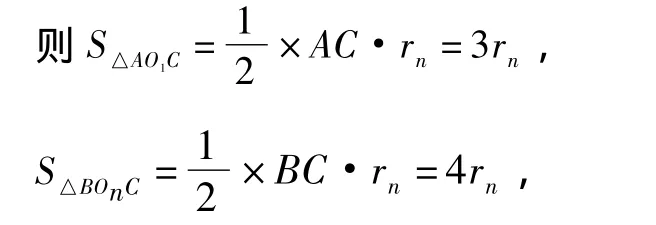
∵ 等圓⊙O1，⊙O2，…，⊙On依次外切，且均與 AB邊相切，

∴ ⊙O1，⊙O2，…，⊙On均在直線 O1On上，

且 O1On∥AB.

∴ O1On=(n－2)2rn+2rn=2(n－1)rn，

點評 本題是探索相切圓的半徑規(guī)律型問題，要求同學們善于觀察圖形，能從最簡單情況探究問題的解法中得到啟示，從而根據(jù)已有的知識經(jīng)驗對復雜圖形進行分解計算與探究，找出其中的隱含變化規(guī)律，從而遷移問題的解法推廣得一般的結論.

拓展3 將直角三角形改換成等腰三角形，并變換問題的情境——放置到平面直角坐標系中研究內(nèi)切圓圓心的坐標，進而拓廣探究其旁切圓圓心坐標

例3 (2009年莆田)(1)如圖10，已知，△ABC的周長為 l，面積為 S，其內(nèi)切圓的圓心為 Q，半徑為 r，求證:r=

(2)如圖11，△ABC中，A，B，C三點的坐標分別為A(－3，0)，B(3，0)，C(0，4)，若△ABC 的內(nèi)心為 D，求內(nèi)心點D的坐標;

(3)與三角形的一邊和其他兩邊的延長線相切的圓，叫旁切圓，圓心叫旁心.請求出條件(2)中的△ABC位于第一象限的旁心的坐標.

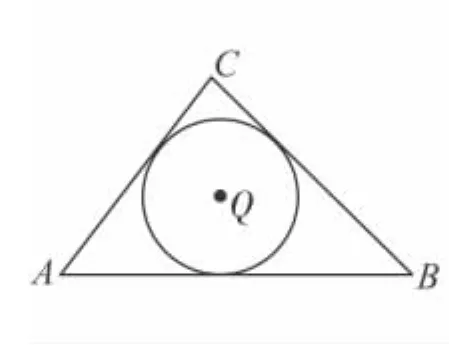
圖10

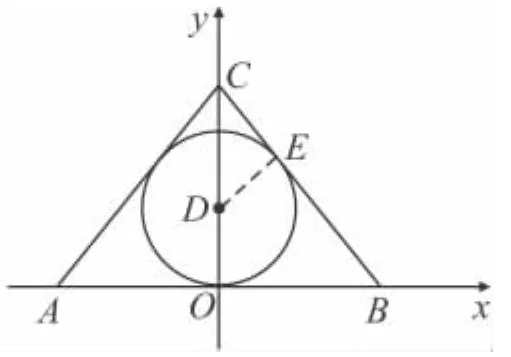
圖11

解析 (1)見拓展1閱讀材料.

(2)解法1 由于點D在y軸上，且⊙D與x軸相切，故點D坐標為(0，r)，因而只需求出⊙D的半徑r即可，受(1)的啟發(fā)可以利用面積作為相等關系列出關于r的方程.

由已知得AB=6，AC=5，所以，

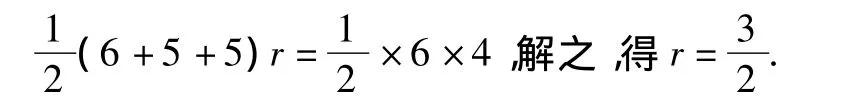
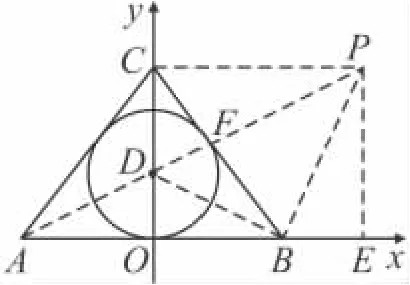
圖12

(3)根據(jù)旁切圓的定義，分別作∠BAC的平分線及∠BCA的外角的平分線，設它們相交于點P，則點P就是第一象限內(nèi)旁切圓的圓心.過點P作 PE⊥x軸于點 E，連接BD，BP，設點 P(a，b).

解法1 利用相似三角形性質(zhì)列出關于a，b的方程組求解即可.

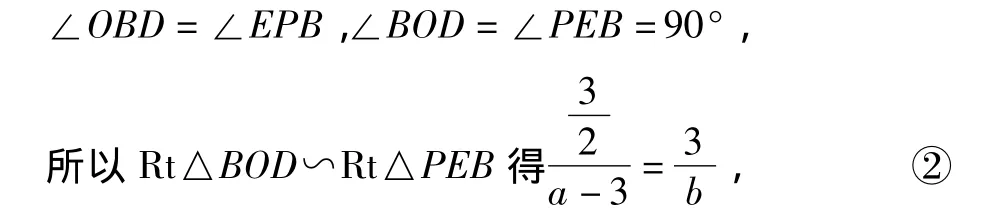
由BD平分∠ABC，BP平分∠ABC的外角，

所以∠PBD=90°.

根據(jù)等角的余角相等可知

聯(lián)立①②解方程組得b=4，a=5故點P的坐標為(5，4).

解法2 可以證明等腰△CAB頂角∠ACB的外角平分線與底邊AB平行，即PC∥AB，又點P在射線AD上，所以P可以看作是直線CP與射線AD的交點.由待定系數(shù)法可以求得直線AD的解析式為y=x，顯然直線CP的解析式為y=4，聯(lián)立方程組解之，P(5，4).得所以點 的坐標為

點評 本題又見于人教版數(shù)學九年級上冊第106頁練習題2，將△ABC特殊化成為等腰三角形，并將其放置于平面直角坐標系中，換一個視角探究內(nèi)切圓的圓心的坐標，進而拓展進一步探究旁切圓的圓心坐標，意在考查學生靈活遷移知識解決問題的能力.解決問題的思路入手較寬，關注了不同層次學生的數(shù)學學習水平，為張揚學生的個性創(chuàng)設了一個比較人性化的數(shù)學環(huán)境，整個試題的設計由簡單到復雜，梯度合理，在學生思維的最近發(fā)展區(qū)設計問題，拓展適度，符合學生的認知規(guī)律.體現(xiàn)了“承認差異，尊重個性，不同的人在數(shù)學上有不同的發(fā)展”數(shù)學理念.

3 習題資源開發(fā)引發(fā)思考

3.1 應突出數(shù)學思想方法對解題教學的導航

數(shù)學思想方法是數(shù)學知識在更高層次上的抽象和概括，它蘊含在數(shù)學知識的發(fā)生、發(fā)展和應用的過程中，有待我們從問題的探究和解決過程中去發(fā)現(xiàn)和挖掘，進而讓學生銘記在心，只有理解上述解法探究中運用了方程(引例解法1、2)、轉化(將圖形的面積進行分割轉化)、類比、特殊到一般等數(shù)學思想方法.數(shù)學思想方法，才能在解決類似的數(shù)學問題時自覺地去應用.

3.2 習題拓展應設計遞進型問題，以提升學生探究能力

問題是數(shù)學的心臟，問題的解決是數(shù)學思維的核心，教學中有意識地將原問題拓展延伸，可以有效地培養(yǎng)學生的問題意識與探究能力.在平時習題的教學過程中應當以學生原有的知識經(jīng)驗作為新知識的生長點，引導學生從原有的知識經(jīng)驗中，生長新的知識經(jīng)驗，使設計的問題永遠處于“學生最近發(fā)展區(qū)”.改編課本習題應當注意與習題體現(xiàn)的數(shù)學知識、方法、思維規(guī)律的關聯(lián)性，讓解題思路這一不變的“暗線”貫穿始終，當一個問題涉及到相當多的乃至無窮多的情形時，可從問題的簡單情形或特殊情況入手，通過簡單的情形或特殊情形的觀察與探索，從中發(fā)現(xiàn)一般規(guī)律，或作出某種猜想，從而找到解決問題的途徑或方法.這樣從最簡單的問題入手通過對數(shù)學問題多角度、多層次、多方位的討論和思考，層層推進，不斷揭示問題的本質(zhì)，引導學生從“變”的現(xiàn)象中發(fā)現(xiàn)“不變”的本質(zhì)，從“不變”的本質(zhì)中探索出“變”的規(guī)律，從而提升學生獨立思考和解決問題的能力，激發(fā)學生大膽參與，勇于探索的精神.

20110328)