與圓錐曲線切線有關的幾個定值問題

●(元濟高級中學 浙江海鹽 314300)

唯物辨證法告訴我們:運動是絕對的,靜止是相對的;世上萬物都是動中蘊靜，動靜相依的.經過研究，筆者發現這一規律在圓錐曲線的切線中也有所體現:盡管有時圓錐曲線的切線與圓錐曲線有著相對任意的動態位置，但仍會有一些視為靜態的結論,譬如結果為“定值”或“過定點”等等.限于篇幅,這里僅舉幾個關于“定值”的例子,以饗讀者.

例1過橢圓的2個焦點引橢圓任一切線的2條垂線，則這2條垂線長的積為定值.

又設2個焦點的坐標為(c,0)，(-c,0),則焦點到切線的垂線長的積為

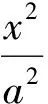
圖1

證明由于橢圓過直徑端點的切線平行于它的共軛直徑,因此過2條共軛直徑的端點引橢圓的切線所圍成的平行四邊形相鄰的2條邊長分別為共軛直徑長.

設2條直徑的交角為φ=β-α,則

sinφ=sinβcosα-cosβsinα=

故該平行四邊形面積為

例3過橢圓上任意一點M所作的切線，與過這橢圓長軸端點A,A′的2條切線分別交于點N,N′，則AN·A′N′為定值.

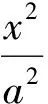
過橢圓長軸端點A，A′的2條切線方程為

式(1)，式(2)消去x,得

(3)

而長軸端點處的2條切線x2-a2=0都與x軸垂直,因此AN,A′N′的積即為方程(3)的2個根之積,于是

圖2

例4過雙曲線上任意一點P的切線與2條漸近線交于點A,B，則雙曲線中心O與A,B所成三角形的面積為定值.

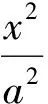
解得

S△OAB=S△AOM+S△OBM=

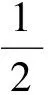
例5過拋物線y=x2上的任意一點P(原點除外)引切線l和x軸,y軸分別交于點Q,R，則|PR|∶|PQ|是定值.

圖3

圖4

整理得

故點M(0，pt)到圓的切線長的平方為

即切線長|MT|為定值.