TD-LTE系統中基于奇異值分解的高效波束賦形方法*

(上海貝爾股份有限公司，上海 200070)

1 引 言

作為由我國自主提出的第三代移動通信(3G)標準TD-SCDMA的演進標準， TD-LTE的標準化和面向未來商用的系統試驗工作，近年來在無線通信領域內受到了極大的關注[1-2]。目前，TD-LTE系統外場大規模組網試驗即將展開。出于TD-LTE系統與TD-SCDMA系統共天線共站址以盡可能降低網絡演進成本的考慮，下行鏈路8發2收的TD-LTE系統已被確定為是一種主流的用于室外覆蓋的TD-LTE系統形式[2]。

TD-LTE系統和TD-SCDMA系統同屬時分雙工(TDD)系統范疇，相對頻分雙工(FDD)系統具有天然的上下行信道互易性的特點，更便于采用“波束賦形”(或“智能天線”)技術[3-4]，用以提高系統下行的傳輸性能。作為TD-SCDMA系統中的一項特色技術，波束賦形技術能否在TD-LTE系統中進一步地成功演進，并用于實際的網絡部署中，提高TD-LTE系統下行傳輸的系統性能，是TD-LTE系統建設中一項極受關注的熱點課題[2]。

在TD-LTE系統中，基站(eNodeB)基于終端(UE)上行兩根天線交替發送探測參考信號(SRS)所獲得的矩陣信道進行下行波束賦形，相對于基于UE上行固定一根天線發送SRS所獲得的向量信道進行下行波束賦形，能獲得更好的下行傳輸性能。在工程上，基于矩陣信道的波束賦形通常采用對信道相關矩陣進行迭代處理的方法獲得波束賦形天線加權向量，用于下行波束賦形[5]。但是，為了獲得逼近精確的加權向量，需進行多次迭代，復雜度較大且存在由于初始迭代向量選取不當導致迭代不能收斂的風險。

為了克服傳統方法復雜度較大且可能不收斂的問題，本文提出一種TD-LTE系統中基于奇異值分解(SVD)的高效波束賦形方法。該方法利用系統終端側僅有兩根天線的系統特性，有針對性地采用下行矩陣信道SVD獲得波束賦形天線加權向量，不僅能夠直接獲得精確的天線加權向量，而且，相對傳統的迭代方法可以大幅降低復雜度。

2 TD-LTE系統

2.1 天線配置

TD-LTE系統天線配置如圖1所示。在該系統中，基站側配置N根天線，具有同一時刻N發或N收的能力；終端側配置2根天線，具有同一時刻1發或2收的能力[1]。與之對應，在一個TD-LTE的上行發送間隔，上行鏈路(從終端到基站的方向)為1發N收；在一個TD-LTE的下行發送間隔，下行鏈路(從基站到終端的方向)為N發2收。

考慮到目前下行鏈路8發2收的TD-LTE系統已被確定為是一種主流的用于室外覆蓋的TD-LTE系統，本文重點關注基站側配置N=8根天線的TD-LTE系統，進行與之對應的波束賦形方法性能和復雜度分析。盡管如此，本文所提的波束賦形方法以及復雜度分析可以直接推廣到基站側配置任意N≥2根天線的系統，并在N較大時獲得類似結論。

2.2 幀結構

TD-LTE系統的上下行鏈路使用相同頻率，基于所配置的幀結構采用時分雙工(TDD)的方式進行復用[1]。一個TD-LTE幀結構配置例如圖2所示，其中，上下行配置號為1，對應一個無線幀中的子幀類型為“DSUUDDSUUD”; 特殊子幀配置號為7，對應特殊子幀中DwPTS、GP和UpPTS 3個域的長度比例為10∶2∶2。

圖2 一個TD-LTE幀結構配置例：上下行配置1+特殊子幀配置7

3 基于上下行信道互易性的波束賦形

TD-LTE系統屬于TDD系統范疇，上下行鏈路使用相同頻率，相對FDD系統具有天然的上下行信道互易性的特點，更便于利用上行信道的估計結果進行下行波束賦形。

特別地，在TD-LTE系統中，在上行子幀的最后一個符號或UpPTS的最后兩個符號里，終端可被配置按照一定的模板發送上行SRS[1]，基站可以基于終端發送的SRS估計出上行信道，并利用上下行信道的互易性，基于上行信道的估計結果計算出下行波束賦形的天線加權向量，用于波束賦形。

SRS的發送可被配置為通過終端上行固定一根天線發送(如通過終端發送天線0發送)或者終端上行兩根天線交替發送(如通過終端發送天線0和1交替發送)。對于終端上行固定一根天線的SRS發送，基站基于發送的SRS可以估計出頻域每個無線塊(Radio Block, RB)(包含12個連續子載波，為終端進行與下行波束賦形相對應的信道估計的最小單位)上從終端SRS發送天線(如前文所提的天線0)到基站天線間的向量信道：

h0=[h0,0,h0,1,h0,2,…,h0,N-1]

(1)

式中，h0,n(n=0,1,2,…,N-1)為某RB上終端SRS發送天線與基站天線n間的信道。

基于上下行信道互易性，假設上下行信道相同，為了達到最大的相對終端SRS發送天線的波束賦形增益(即對應下行采用終端SRS發送天線進行接收時獲得最大的下行發送信號接收能量的情形)，對應下行波束賦形天線加權向量w(1-Ant)為

(2)

由式(2)可見，對于終端上行固定一根天線發送SRS的情形，可以容易地獲得對應的下行波束賦形天線加權向量。對于一個N維的向量信道h0，計算對應的下行波束賦形天線加權向量的復雜度(表示用所需的復乘次數)僅為

O(1-Ant)=2N+1

(3)

但是，由于下行波束賦形天線加權向量僅基于部分下行信道計算得到，不能保證實際終端在下行通過兩天線進行分集接收時能獲得最大的波束賦形增益(或信號接收能量)。

如果終端被配置為通過上行兩根天線交替地進行SRS發送，基站基于發送的SRS可以估計出頻域每個RB上從終端所有兩根天線(如前文所提的天線0和1)到基站天線間的完整的矩陣信道：

(4)

式中，hm,n(m=0,1；n=0,1,2，…,N-1)為某RB上終端天線m與基站天線n間的信道。基于上下行信道互易性，假設上下行信道相同，為了達到最大的終端進行兩天線分集接收時的波束賦形增益(或信號接收能量)，對應下行波束賦形天線加權向量w(2-Ant)應滿足：

(5)

由式(5)可見，對于UE上行兩根天線交替發送SRS的情形，對應的下行波束賦形天線加權向量為所獲得的N×N維信道相關矩陣R=HHH的主特征向量(即對矩陣進行特征值分解后，與矩陣最大特征值相對應的特征向量，或有多個相等的最大特征值時對應特征向量的線性組合)，或者等效地，為所獲得的矩陣信道H的主右奇異向量(對矩陣進行奇異值分解后，與矩陣最大奇異值相對應的右奇異向量)。

4 傳統的基于矩陣信道的波束賦形方法及其分析

傳統地，在工程上常采用如下的迭代方法獲得對應矩陣信道H的波束賦形天線加權向量w(2-Ant)，即式(5)的解。

輸入：

M×N維矩陣信道H

輸出：

對應H的N維波束賦形天線加權向量W(2-Ant)

過程：

(1)計算N×N維信道相關矩陣R

R=HHH

(6)

(2)迭代獲取C的主特征向量W(2-Ant)

1)初始化

N維初始迭代向量e0=einit

(7)

2)迭代：i=1,2,3,…,Nitr

ei=Rei-1

(8)

3)輸出

W(2-Ant)=eNitr/‖eNitr‖

(9)

上述迭代方法是一種通用方法，可應用于任意M×N維矩陣信道H，未針對終端僅配置2根天線的TD-LTE系統情形(即2×N維矩陣信道H)進行特別的優化。

對TD-LTE系統中基于矩陣信道的波束賦形，基站可獲得的矩陣信道H為2×N維，如式(4)所示。對應地，如采用上述迭代方法獲得波束賦形天線加權向量，可將式(6)的信道相關矩陣R表示為如下的特征值分解后的形式：

(10)

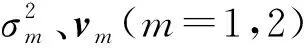
(11)

式中，主特征向量v1方向上的能量和次特征向量v2方向上的能量之比為

(12)

(2)當einit選取得當時，為了獲得逼近期望的加權向量，也常需要進行多次迭代，復雜度較大。

對所關注的2×N維矩陣信道H情形，式(6)、式(8)和式(9)的復雜度(表示用所需的復乘次數)分別為N2+N、N2和2N+1，如進行Nitr次迭代，總共所需的復雜度為

(13)

對于8發2收TD-LTE系統中基于矩陣信道的波束賦形，如迭代次數Nitr=20，復雜度為1 369次復乘。

5 新的基于奇異值分解的高效波束賦形方法

針對傳統的基于矩陣信道的迭代波束賦形方法復雜度較大且可能不收斂的問題，本節提出一種基于奇異值分解的高效波束賦形方法。該方法利用系統終端側僅有2根天線的系統特性，采用有針對性的基于2×2矩陣特征值分解公式的矩陣信道奇異值分解，能夠直接獲得精確的波束賦形天線加權向量，而且，相對于傳統的迭代方法可大幅降低復雜度。

如前所述，基于矩陣信道H的波束賦形天線加權向量w(2-Ant)，即式(5)的解，等效地也為矩陣信道H的主右奇異向量；因此，2×N維矩陣信道H的奇異值分解可表示為

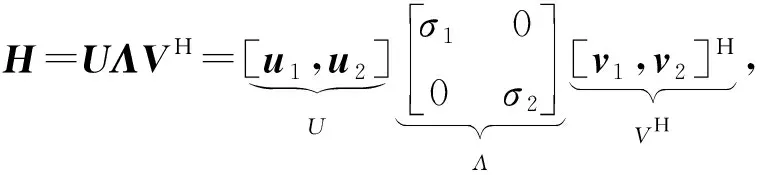
(14)

式中，U和V分別為2×2和N×N的酉陣，Λ為2×2的對角陣，v1為期望得到的對應最大奇異值σ1的右奇異向量。

考慮到TD-LTE系統終端端側僅有2根天線，以至于H其中一維(即H的行)的維度僅為2，且2×2矩陣的特征值分解存在高效的計算公式，為了獲得H的主右奇異向量v1(即對應波束賦形天線加權向量w(2-Ant))，所提方法的基本思想為：

首先，利用2×2矩陣的特征值分解公式，計算C=HHH的特征值分解輸出中“必要”的部分(以便用于后續主右奇異向量v1的計算)。

2×2矩陣C的特征值分解公式如下：

C=UΣUH

(15)

其中：

(16)

需通過2×2矩陣的特征值分解公式計算得到u1和δ1。

在本文中，利用高效的2×2矩陣ansatz特征值分解公式[6]計算特征值分解的必要輸出。實際上，2×2矩陣特征值分解公式并非是唯一的。在工程實現中，也可根據特定硬件實現的方便，選擇其它的2×2矩陣特征值分解公式進行計算，如Takagi 因式分解公式，本文就不再贅述。

然后，基于通過特征值分解獲得的u1、δ1，以及原始的H計算得到v1。

特別地，據式(14)和式(16)，可直接得到：

(17)

詳細的方法計算流程如下所示，其中，sign(·)為取符號操作。

輸入：

2×N維矩陣信道H

輸出：

對應H的N維波束賦形天線加權向量w(2-Ant)

過程：

(1)計算2×2維信道相關矩陣C

(19)

(2)利用高效的2×2矩陣ansatz特征值分解公式計算特征值分解的必要輸出u1和δ1

(20)

(21)

(22)

γ1=c1,1+β,γ2=c2,2-β

(23)

如果γ1≥γ2,

u1=[s,t2s]T,δ1=γ1

(24)

否則，

u1=[-t1s,s]T,δ1=γ2

(25)

(3)基于u1、δ1，以及H計算得到H的主右奇異向量v1(即對應波束賦形天線加權向量w(2-Ant))

(26)

可見，式(19)～(24)或式(25)，以及式(26)的復雜度(表示用所需的復乘次數)分別為3N、5、1、3、0、1以及2N+3，方法總共所需的復雜度為

(18)

對于8發2收TD-LTE系統中基于矩陣信道的波束賦形，復雜度為53次復乘，大大低于傳統迭代方法。

6 仿真結果及分析

考慮圖1所示的TD-LTE系統，基站側配置N=8根天線，終端側配置2根天線；幀結構配置如圖2所示；信道采用3GPP定義的SCM信道模型建模[7]，信道場景為城市宏小區(Urban Macro)。

圖3對本文涉及的幾種波束賦形方法進行了仿真性能比較。從圖中可以看到，基于矩陣信道的波束賦形相對基于向量信道的波束賦形在誤塊率(BLER)等于0.1處具有1.5 dB的信噪比(SNR)增益。其原因在于，前者使用了完整的矩陣信道信息計算下行波束賦形天線加權向量，使得終端在兩天線分集接收時，獲得了最大的波束賦形增益。

從圖中還可以看到，對基于矩陣信道的波束賦形，所提方法與進行了多次迭代(以使性能收斂)的傳統方法相比，性能非常接近。其原因在于，所提方法通過奇異值分解可以獲得精確的波束賦形天線加權向量，具有最優的性能。但是，由于所提方法是直接計算得到期望的加權向量，無需進行多次迭代，并且在計算過程中充分利用了TD-LTE系統終端側僅有2根天線的系統特性對奇異值分解算法進行了優化，相對傳統方法復雜度大幅降低。特別地，如前文分析，傳統方法計算一次波束賦形加權向量需1 369次復乘；新的方法僅需53次復乘。仿真結果和復雜度分析驗證了所提方法的有效性。

圖3 波束賦形方法性能比較

7 結 論

針對TD-LTE系統中基于矩陣信道的波束賦形問題，本文提出了一種基于奇異值分解的波束賦形方法。該方法利用系統終端側僅有2根天線的系統特性，采用基于2×2矩陣特征值分解公式的矩陣信道奇異值分解獲得波束賦形天線加權向量，用于下行波束賦形。理論分析和仿真結果表明，所提方法不僅可以獲得精確的波束賦形天線加權向量，具有最優的性能，而且，相對傳統基于迭代波束賦形方法在相當程度上降低了復雜度，是一種在工程上既有效又實用的波束賦形方法。

參考文獻：

[1] 3GPP.TS 36.211 V8.9.0,Physical Channels and Modulation[S].

[2] 2010ZX03002-002，TD-LTE面向商用基站研發[S].

2010ZX03002-002，TD-LTE commercial eNodeB R&D [S].(in Chinese)

[3] Thomas T A, Mondai B, Vook F W. Methods for Switching Between Long Term and Short Term Transmit Beamforming in OFDM[C]//Proceedings of VTC′2007-Spring.Dublin,Ireland:IEEE,2007:574-578.

[4] 李亞麟，樊迅，胡波，等.天線校準誤差建模即對開環波束賦形技術的影響[J].電訊技術，2010,50(3)：45-48.

LI Ya-lin,FAN Xun, HU Bo, et al. Modeling of Antenna Calibration Error and its Impact on Open-Loop Beam forming [J]. Telecommunication Engineering, 2010,50 (3):45-48.(in Chinese)

[5] Todd K M, Wynn C S. Mathematical Methods and Algorithms for Signal Processing [M].London:Prentice Hall,1999.

[6] Thomas H. Routines for the diagonalization of complex matrices [M].Germany:[s.n.],2006.

[7] 3GPP.TR 25.996 V9.0.0，Spacial Channel Model for Multiple Input Multiple Output (MIMO) Simulations [S].