CAPM模型中β系數的非參數估計

○花俊洲 （上海金融學院 上海 201209）

CAPM模型中β系數的非參數估計

○花俊洲 （上海金融學院 上海 201209）

在資產定價模型的實證檢驗中，由于證券期望收益與系數β值之間未必存在嚴格的線性關系，因此使用一般線性回歸方法對β進行估計必然會導致模型的不準確。作為對這種估計方法的修正，本文提出了可變系數回歸模型，利用局部加權最小二乘估計方法對模型中的系數β進行估計，并研究了模型中局部權系統的決定問題，該模型是一般線性回歸模型的推廣。由于系數的可變性，使得估計結果更適應實際數據的變化規律，從而估計結果更為精確，該方法也為風險管理和監督提供了較為有用的數理工具。

CAPM β系數 可變系數回歸模型 局部加權最小二乘估計

一、理論綜述

資產定價問題是近幾十年來西方金融理論中發展最快的一個領域。投資組合理論由亨利·馬柯維茨（H.M.Markovitz）于1952年創立，形成了現代資產定價理論。它把投資者的投資選擇問題系統闡述為不確定性條件下投資者效用最大化問題，這標志著現代證券理論研究進入了定量分析階段。馬柯維茨的研究在理論上解決了證券組合的選擇問題，但因其需要巨大的計算量而難以得到廣泛應用。1963年，威廉·夏普（Sharpe）提出了簡化形式的計算方法，即單指數模型。1965年前后，Sharp等人提出著名的資本資產定價模型（CAPM），使投資組合理論應用于整個經濟學領域。這一模型在現實的投資組合績效、證券估價、確定資本預算及管理公共事業股票中得到了普遍應用。

在一組嚴格的假定下，CAPM模型可簡單地表達為：

ri=αi+βirM+εi

其中ri表示證券或組合i的期望收益率，αi表示獨立于市場部分的收益率，rM表示市場組合期望收益率，βi為證券或組合的系統風險系數，εi為隨機誤差。

然而，大量的實證研究又發現一些CAPM無法解釋的異常現象，諸如公司的規模、贏利—價格比、現金流量—價格比、歷史銷售增長率、歷史收益率表現等因素都會對股票的期望收益率產生一定的影響。針對證券收益受多種因素的影響，馬歇爾（Marshell）和布努姆（Blume）等人又提出了多因素模型。

多因素模型（MPM）由于具有較強的解釋性而成為目前投資實踐中的主導模型。從統計的觀點看，多因素模型通過許多因子來確定證券的價格，所考慮因素的范圍較廣。與CAPM模型僅從證券市場本身的歷史來研究股價不同，多因素模型把證券的價格與通貨膨脹率、失業率、工業生產總值、利率水平、匯率水平等經濟因素聯系起來，從而使模型能更好地反應現實情況。

多因素模型的簡潔表達如下：

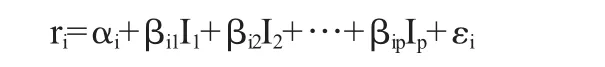
其中：Ij（j=1，2，…，p）表示影響收益率的第j個因素，βij表示證券或組合i對因素Ij的敏感度，其他符號表示同上。可以看出，多因素模型認為股票的超額收益由兩部分組成，即由各因素作用影響的收益部分和無法由各因素解釋的收益部分。

1976年，羅斯（Ross）通過放松有效市場的假設，提出了套利定價理論（APT），對CAPM模型作了進一步修訂，其重要特性是合理且簡單易懂。在均衡狀態下，所有被選擇的證券組合來自被考察的資產集并滿足無風險就無收益的條件，而且對其風險性資產的定價不依賴于有效市場證券組合的選擇。它假設任一證券的收益率是由k個因素的線性函數決定的，其方程為：

其中：Eri是第i種資產的期望收益率，Fj（j=1，2，…，k）表示第j種因素指數的收益，βij是第i種資產的收益對第j個因素的靈敏度，εi是第i種資產均值為零的特殊收益。

盡管上述三大資產定價理論在經濟解釋和應用上有很大區別，但在數學處理上卻有共同之處，即假定證券期望收益與系數β值之間存在嚴格的線性關系，并使用一般線性回歸方法對其系數進行估計。然而，實證檢驗表明，證券期望收益與β值之間是否存在嚴格的線性關系仍然值得懷疑。Black等以及Fama和MecBeth對美國證券市場的實證研究發現，證券的期望收益與β之間確實存在一種正的線性關系，然而在1992年Fama和French采用與以前不同的樣本數據研究發現，證券的期望收益與他們所設計的β之間幾乎不存在相關性。陳浪南和屈文洲針對上海證券市場的實證研究表明，β對股票期望收益的解釋能力并不是很強。

很顯然，假如實際中證券期望收益與β值之間不存在嚴格的線性關系時，使用上面的一般線性回歸方法來估計系數β，必然會導致結果的不正確。本文針對這種不足，提出了一個可變系數的回歸模型，并使用局部加權最小二乘估計法來估計系數β，使得估計結果更為準確，能夠更加適應數據自身的變化規律，也更貼近于數據的實際要求。

二、可變系數回歸模型的提出

首先來回顧一般采用的線性回歸方法。為了便于數學表達，可以把上述三大定價定理抽象為統一的數學模型。

定義1（一般線性回歸模型）：假定對某種證券或組合有n組歷史觀測數據（Yi，xi），其中Yi表示收益率，xi=（xi1，xi2，…，xip）T表示影響該證券或組合收益率的因素，對于隨機變量Y1，Y2，…，Yn一般的線性回歸模型如下：

（Ⅰ） Y1，Y2，…，Yn相互獨立，并且Yi～N（μi，σ2），i=1，2，…，n

其中xi0=1；μi=E（Yi），i=1，2，…，n。

通常情況下，可以用最小二乘方法來對該模型進行估計。

定義2（可變系數回歸模型）：假定對某種證券或組合在不同的觀測“位置”Vi，有n組歷史觀測數據（Yi，xi），i=1，2，…，n，對于隨機變量Y1，Y2，…，Yn在“位置”V點的可變系數回歸模型定義如下：

（Ⅰ） Y1，Y2，…，Yn相互獨立，并且Yi～N（μi，σ2），i=1，2，…，n

其中V∈D，D是一個帶有距離函數d（·，·）的m維度量空間，V可以解釋為觀測數據x所對應的“位置”，比如：當V=t為一維時間標量時，就表示按時間順序觀測到的數據x，當V=（x，y，z）為三維向量時，就可以表示為在空間地理位置（x，y，z）上觀測到數據x，當V=（x，y，z，t）為四維空間時，則表示t時刻在空間地理位置（x，y，z）上觀測到數據x，如此等等。D中的距離d（·，·）可以根據問題的實際背景具體化，除了通常使用的歐氏距離之外，它還可以取作兩觀測點之間的社會環境、經濟環境、自然環境的相似性度量等等。在此基礎上，我們的模型可看成是隨觀測數據x的“位置”V變化而變化模型系數的變系數回歸模型。β0（·），β1（·），…，βp（·）是p+1個定義在空間D的某一子集上的函數。

盡管可變系數線性模型形式上看起來很具體，但它實際包含了許多熟知的線性回歸模型作為其特例，如：

（Ⅰ）如果βj（V）=βj，j＝0，1，…，p是p+1個未知常數，那么模型（1）便是一般線性回歸模型。

（Ⅱ）取D?RP，V=x且β1（x）=…=βp（x）=0，則模型（1）便為μ=β0（x）；由于β0（x）是任意函數，所以這正是非參數回歸模型。

（III）如果取D=[0，+∞)，V=t是第t個觀測值在被獲得的時間點，那么模型（1）便為：μt=β0（t）+β1（t）xt1+…+βp（t）xtp，t=t1，t2，…，tn。這個模型便是熟知的動態線性回歸模型。

因此，可變系數回歸模型，是原來的一般線性回歸模型的推廣。對于模型（1），可以通過下面的局部加權最小二乘方法來估計系數。

南通歷史上有許多英雄人物，深受儒家經內圣外王思想的影響，努力在各方面完善自我提升自身的修養能力，在此基礎上，憑借著“己欲立而立人，己欲達而達人”的理念，將自身理想信念外擴，從而造福桑梓服務社會。

三、可變系數回歸模型的估計

利用非參數回歸中局部擬合的思想，通過對對數似然函數施加適當的局部權，再利用極大似然原理得到所關心的局部估計量，適合非參數回歸擬合問題。這種思想自提出以后，目前已得到廣泛的研究，本文正是利用這種思想來進行局部加權估計的。

一般地，給定任何一點V∈D，這里xT=（x1，x2，…，xp）∈M，對所有的觀測點（Yi；xi1，xi2，…xin）i=1，2，…，n，它們均提供了μ=EY在給定點V的信息，這些信息可用以估計系數β0（V），β1（V），…，βp（V），然而不同的觀測值對在給定點處V的系數估計有不同的重要性，這種重要程度可以通過一組權來對相應似然函數中的各項作調整。

設在給定點V處的一組權為：w1（V），w2（V），…，wn（V），其中第i個權wi（V），相對應于第i個觀測數據（Yi；xi1，xi2，…，xip）。

對于模型（1），不難求得（yi，y2，…，yn）的對數似然函數：

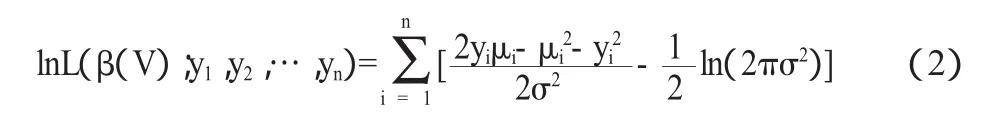
按照局部似然方法，在給定點處V相應于權wi（V），i=1，2，…，n的局部加權似然函數（為方便計，仍記為lnL（β（V）；y1，y2，…，yn））為：

定義2對給定的點V∈D，使（3）式達到最大值的β（V）的值，記為：β^（V）=（β^0（V），β^1（V），…β^p（V））T，稱為β（V）在給定點處V的局部加權最大似然估計量。

由于變系數回歸模型的局部加權最大似然估計量的推導類似于一般線性回歸模型的推導，因此可以不加證明地給出如下結論。

定理1對于變系數回歸模型（1），β（V）在給定點V處的局部加權最大似然估計量由如下方程組來決定：

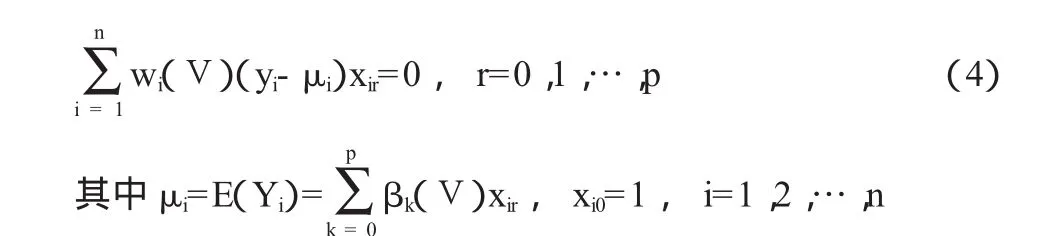
定理2對于變系數回歸模型（1），假定對于任意點V∈D，矩陣XTW1（V）X的逆矩陣均存在，那么β（V）在給定點V處的局部加權最大似然估計量為：

并且，W1（V）=diag（W1（V），W2（V），…Wn（V））為n階對角權矩陣。

證明過程如下：

由定理1，可知似然方程為：

上式可表示為矩陣形式：

其中，β（V）=（β0（V），β1（V），…βp（V）），其他表示同上。

假定對于任意點V∈D，矩陣XTW1（V）X的逆矩陣均存在，則在給定點V處的參數估計值可表示為：β^（V）={XTW1（V）X}-1XTW1（V）Y。

特別地，若對一切的1≤i≤n及任意點V∈D，設定W1（V）=1，那么（6）式就變為：XTY=XTXβ。

此即我們熟知的一般線性回歸模型的正則方程。

四、局部權系統的決定

1、Gauss局部權系統

如前所述，對任意給定點V∈D，第i個權值W1（V）；（i=1，2，…，n）反映了第i組觀測xi=（xi1，xi2，…，xip）T及Yi對估計點V處的參數βk（V）；（k=0，1，…，p）的重要性。一般來說，距給定點V∈D較近的觀測數據對V點處的參數估計影響應該較大，而相距較遠的觀測數據對給定點V處的參數估計影響應該較小，甚至為零。而在變系數廣義線性模型中，觀測值xi=（xi1，xi2，…，xip）T以及x=（x1，x2，…，xp）T所對應的D中的點Vi和V之間的距離以d（Vi，V）來度量。因此，對于較小的d（Vi，V）所對應的觀測點，我們賦予較大的權值，反之，對于較大的d（Vi，V）所對應的觀測點，則賦予較小的權值。

下面采用Gauss局部權系統：

在給定點V∈D處，以d（Vi，V）的Gauss函數為該點的權，即：

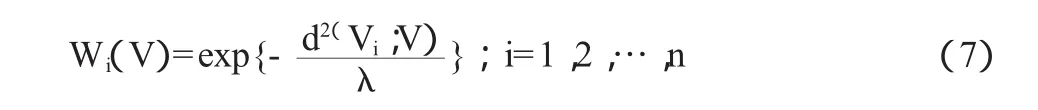
其中λ＞0稱為光滑參數。當λ→0時，只有在觀測點V∈D處，觀測值xi權才為1，其他各觀測點的權值均趨于零。當λ→∞，對于一切i=1，2，…，n均有Wi（V）→1，這時，參數β（V）的局部加權最大似然估計即是通常的最大似然估計。

2、局部權系統中光滑參數的確定

光滑參數的確定問題是非參數回歸中所研究的一個重要課題，針對不同的光滑方法，已經有各種各樣的光滑參數確定方法。在此，我們將利用交叉證實方法（cross-validation）來確定前面所給的局部權系統中的光滑參數λ的值。

由前面可知，在每一給定點V處有觀測值Yi

五、結語

本文主要解決了如下問題。

第一，實證表明，資產定價模型中，證券期望收益與系數β值之間未必存在嚴格的線性關系，針對這種情形，提出了可變系數回歸模型替代原先的一般線性回歸模型來估計系數β，該模型放松了線性的假定，使模型更適應實際數據的變化規律。

第二，利用局部加權最小二乘估計方法對可變系數回歸模型中的系數進行估計。

第三，研究了模型中的局部權系統以及其中光滑參數的決定問題。

從理論角度考慮，該模型由于系數的可變性，使得估計結果更加適應實際數據變化規律，從而估計結果更為精確，該方法也為資產定價研究、風險管理和監督提供了較為有用的數理工具。但由于我國的實際情況，對于復雜數理模型的應用尚缺乏一定的條件，主要是缺乏好的金融數據，大部分金融機構都沒有能夠保留良好的橫截面數據和時間序列數據，這給實證也帶來了不小的麻煩。后續的研究中，我們將克服這些困難，著重于該模型在實際中的檢驗。

（注：本文受上海市教育委員會科研創新項目（09YZ409）、上海教育委員會重點學科建設項目（J51601）資助。）

[1]Angelini，E.，Tollo，G.D.，Roli，A.：A neural network approach for credit risk evaluation[J].The Quarterly Review of Economics and Finance，2008，48（4）.

[2]Black，F.，M.C.Jensen and M.Scholes：The Capital asset pricing model：Some empirical tests，In：M.C.Jensen，ed.，Studies in the theory of capital markets[M].Praeger，New York 1972.

[3]Cox.D.R.：Regression models and life-tables（with discussion）[J].J.R.Statist.Soc.B.，1972（34）.

[4]Fama，E.F.and J.D.Macbeth：Risk，return and Equilibrium：Empirical tests[J].Journal of Political Economy，1973（81）.

[5]Fama，E.F.and French，K.R.：The cross section of expected stock returns[J].The journal of Finance，1992，June（2）.

[6]Fan.J.and Gijbels，I.:Data-driven bandwidth selection in local ploynomial fitting：variale bandwidth and spatial adaptation[J].J. R.Statist.Soc.B.，1995（57）.

[7]Jorgensen，B.：Maximum likelihood estimation and largesample inference for generalized linear and nonlinear models[J]. Biometrika，1983（70）.

[8]Ong，C.-S.，Huang，J.-J.，Tzeng，G.-H.：Building credit scoring modelsusing genetic programming [J].ExpertSystemswith Applications，2005（29）.

[9]West.M.，Harrison.P.J.，Bayesian forcasting and dynamic models [M].Springer，New York，1989.

[10]Tibshirani.R.and Hastie.T.：Local likelihood estimation[J].J. Am.Statist.Ass.，1987（82）.

[11]陳浪南、屈文洲：資本資產定價模型的實證研究[J].經濟研究，2000（4）.

[12]花俊洲、梅長林、吳沖鋒：變系數廣義線性模型及其估計[J].系統科學與數學，2004，24（1）.

（責任編輯：李文斐）

book=1,ebook=67