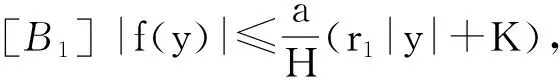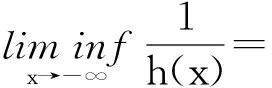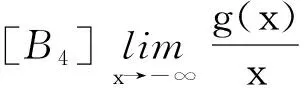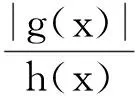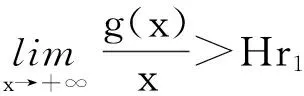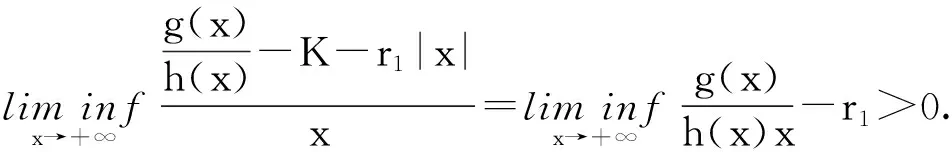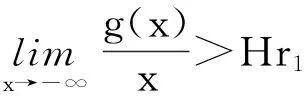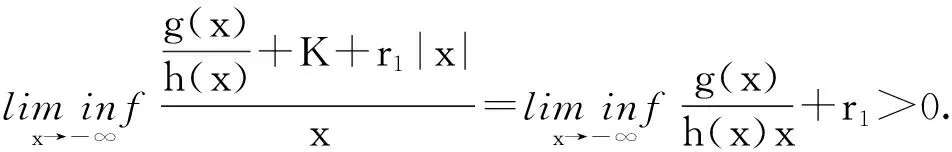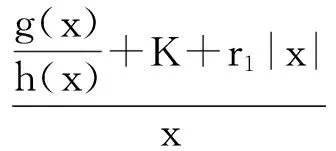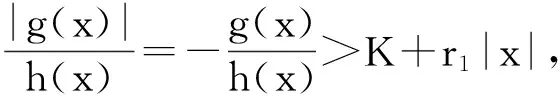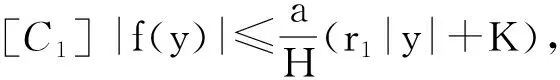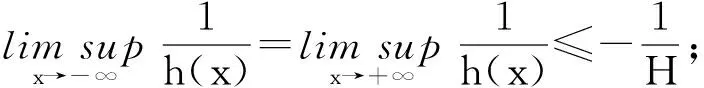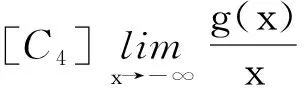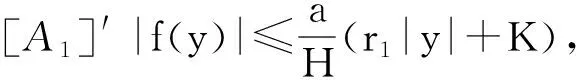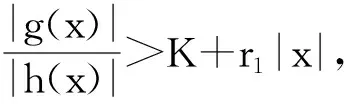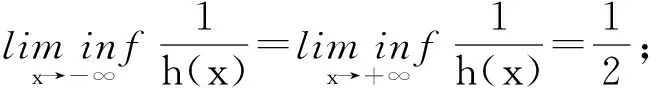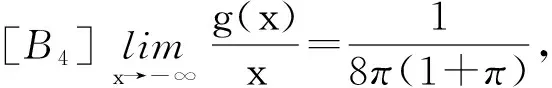具偏差變元泛函微分方程周期解的存在定理
陳新一
(西北民族大學 中國民族信息技術研究院, 甘肅 蘭州 730030)
1 問題的提出
x″(t)+h(x(t))f(x′(t))+g(x(t-τ(t)))=p(t)
(1)
2 主要結果
定理1 如果存在常數r1≥0,r2≥0,a>0,H>0,K>0和D>0,使得
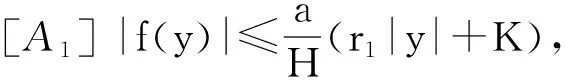
[A2] 0 則當4π[Hr1+(2π+1)r2]<1時,方程(1)至少存在一個2π周期解. 證明 考察下列方程 x″(t)+λh(x(t))f(x′(t))+λg(x(t- (2) 再由積分中值定理知,存在ξ∈[0,2π],使得 h(x(ξ))f(x′(ξ))+g(x(ξ-τ(ξ)))=0. (3) 下面證明存在t*∈[0,2π],使得 (4) |x(ξ-τ(ξ))|≤D. (5) (6) 由(5)和(6)式易見,無論是r1=0還是r1>0,均有 (7) 由于ξ-τ(ξ)∈R,因而一定存在整數k和t*∈[0,2π],使得ξ-τ(ξ)=2kπ+t*,故由(7)式得 于是(4)式成立. 由此得 (8) 令F(z)=4π[Hr1+(2π+1)(r2+z)],z∈[0,+∞). 由題設條件4π[Hr1+(2π+1)r2]<1知F(0)<1. 又F(z)在[0,+∞)上連續,因而存在常數δ0>0,使得 F(z)=4π[Hr1+(2π+1)(r2+z)]<1,z∈(0,δ0]. (9) 4π[Hr1+(2π+1)(r2+ε)]<1. (10) 對上述ε>0,由題設[A4]知,一定存在與λ和x無關的常數ρ>D,使得 (11) 設E1={t:t∈[0,2π],x(t-τ(t))>ρ},E2={t:t∈[0,2π],x(t-τ(t))<-ρ},E3={t:t∈[0,2π],|x(t-τ(t))|≤ρ}. 由(3)式,得到 即 由于 故由上式得 (12) 由E3,E2的定義和(11)式知 (13) 和 (14) 顯然KerL=R. 定義投影算子P和Q分別為 方程(2)即為算子方程Lx=λNx. 根據對(2)周期解界的估計及已知條件,可知對?x∈domL∩?Ω和λ∈(0,1)有Lx≠λNx,對任意x∈KerL∩?Ω,則x=M(>D)或者x=-M,因此有 (15) 作變換H(x,s)=sx+(1-s)g(x),0≤s≤1. 因為對任意x∈?Ω∩KerL及s∈[0,1],我們有xH(x,s)=sx2+(1-s)g(x)x>0,可知H(x,s)是同倫變換,因此 deg{QNx,Ω∩KerL,0}=deg{-g(x),Ω∩KerL,0}= 根據重合度理論可知,方程(1)至少存在一個2π周期解. 注 當h(x(t))≡1時,本文的定理1即是文獻[9]中的定理1. 因此本文的定理1推廣了文獻[9]的結果. 推論1 假設存在常數r1≥0,r2>0,a>0,H>0,K>0和D1>0,使得 [B3]xg(x)>0, 當|x|>D1時; 則當4π[Hr1+(2π+1)r2]<1時,方程(1)至少存在一個2π周期解. 證明 與定理1的條件比較可知,我們只須證明存在常數D>0,使得 (16) 由此存在常數D2>D1,使得 (17) 由此存在常數D3>D1,使得 即 (18) 取D=max{D2,D3},則由(17)和(18)式得(16)式成立. 根據定理1,類似推論1的證明,立即可得如下推論. 推論2 假設存在常數r1≥0,r2>0,a>0,H>0,K>0和D1>0,使得 [C3]xg(x)>0, 當|x|>D1時; 則當4π[Hr1+(2π+1)r2]<1時,方程(1)至少存在一個2π周期解. 類似定理1的證明,可得如下定理. 定理2 如果存在常數r1≥0,r2≥0,a>0,H>0,K>0和D>0,使得 [A2]′ 0 則當4π[Hr1+(2π+1)r2]<1時,方程(1)至少存在一個2π周期解. 由此定理,我們還可得到類似推論1和推論2的結論,這里不再贅述. 例:考慮下列方程 (19) 其中 p(t)=cost. 因而,我們可選取 使得條件 [B3]xg(x)>0, 當|x|>D1時;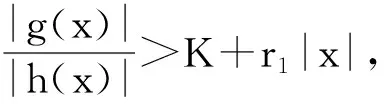
τ(t)))=λp(t),λ∈(0,1).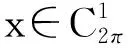
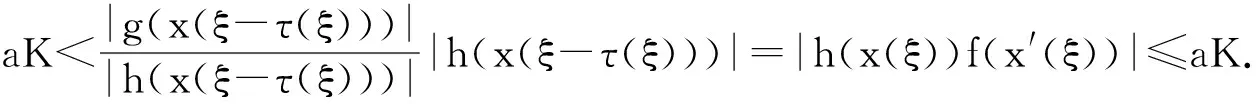
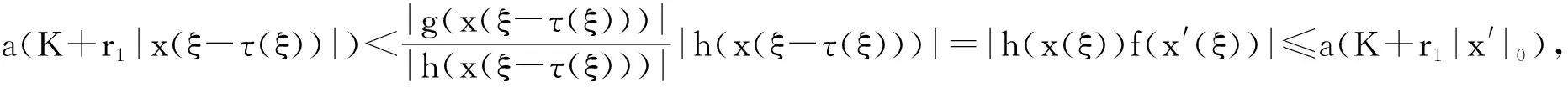
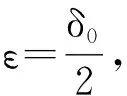
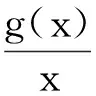
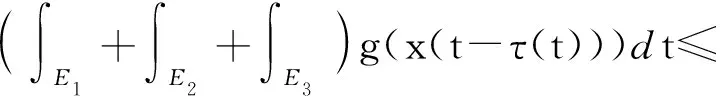
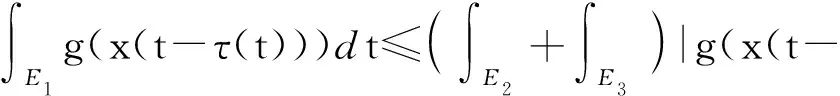
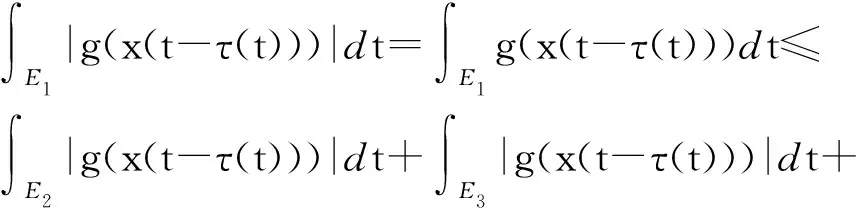
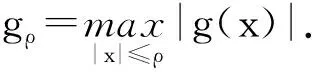
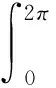
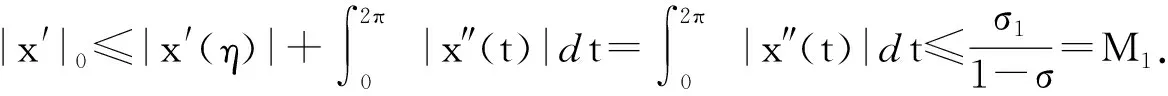
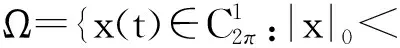
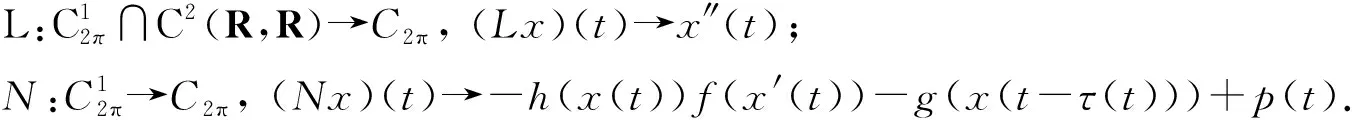

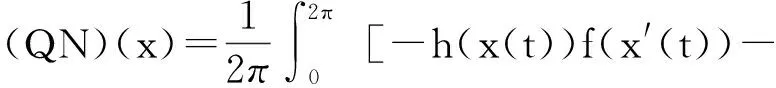
deg{-x,Ω∩KerL,0}=deg{-x,Ω∩R,0}≠0.