正午太陽高度角計算的教學技巧

復旦大學附屬中學（200433） 徐 豐

正午太陽高度角計算的教學技巧

復旦大學附屬中學（200433） 徐 豐

一、把握實質，化繁為簡進行記憶。

在地球公轉一節中，太陽高度角的分析計算為教學的難點、要點，為了解決此問題，有的輔導書上提供了一些計算方法，比如：

1．正午太陽高度角計算公式，既H=90o-|當地緯度±直射點緯度|，H代表當地正午太陽高度，當地緯度指所要求某地的緯度，直射點緯度是指此時直射點所在的緯度，如果當地緯度與直射點緯度在同一半球用減號，若在不同半球用加號，然后取絕對值。

2．正午太陽高度的大小：H=90°-｜φ-δ｜。式中H為正午太陽高度；φ為當地緯度，取正值；δ為太陽直射點的緯度，當地夏半年取正值，冬半年取負值。

應該說這些公式的實質是一樣的，采用套入這些公式進行解題的方法也是比較規范和方便的。然而在實際教學過程中，不少學生使用這些公式時會出現記憶上的前背后忘，要不就是在應對變幻題型時發生公式套入用反了的狀況。這些情況的產生主要源于學生對問題的本質缺乏理解記憶而采用了死記硬背的方式機械地進行記憶。如果在課堂教學過程中能夠結合圖示采用數理幾何方法進行分析論證，使學生理解從計算到結果的整個過程，就能使學生一勞永逸地牢固掌握正午太陽高度角計算的技巧，從容應對變幻的題型。

為了便于學生記憶，首先可以把解題方法簡單地歸納為“90°減夾角”。

接下來下可以利用幾何方法證明某一時期某地的正午太陽高度角為90°減去太陽直射點所在緯度與所求地點的緯度之夾角度數，簡單記為 “90°減夾角”。以下分兩種情況具體分析：

1．當太陽直射點緯度與所求地緯度在同一半球或其中一點在赤道上時。

如圖1所示，當A點為太陽直射點所在，B為所求緯度此時的正午太陽照射點；則∠j為A、B兩點夾角（銳角）。過點B做切線，則角a即為所求的緯度的正午太陽高度角。

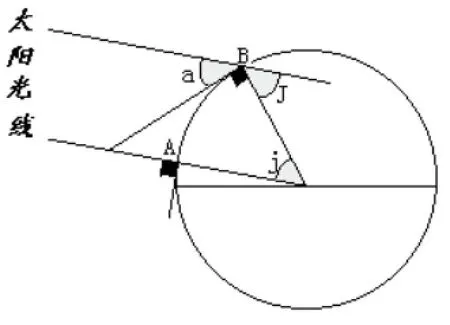
圖1

由幾何方法可推導：由于太陽光線對于地球而言可近似看作平行光，根據兩直線平行內錯角相等的原理，∠J=∠j ，則∠a =（90°—∠J）=（90°—∠j）。也就證明了角a等于90°減去A、B兩點之緯度夾角度數，即“90°減夾角”。

2．當太陽直射點所在緯度與所求地點的緯度在不同半球時。如圖2所示，同理可用來證明：當A點為太陽直射點、B為所求緯度正午太陽照射點時，∠j為A、B兩點夾角，∠a為所求的緯度的正午太陽高度角。因為∠a=∠D，則∠a =∠D=（90°—∠j）也就是角a等于90°減去A、B兩點緯度的夾角，同樣可簡單歸結為“90°減夾角”。需要特別注意的是，當∠j大于90°時，說明此時B點處于極夜，這在后面的應用中將會具體提到。

綜上所述，都證明了除極夜區外，某一天某一地點的正午太陽高度角為90°減去該天太陽直射點所在緯度與所求地點的緯度之夾角度數。這些結果都可以簡單記憶為“九十度減夾角”，不易忘記。而且學生一旦掌握了整個推導的來龍去脈，就不需要只是死記公式，也不會再在夾角大小計算的符號“+”與“-”之間不斷糾結。不管題型變化，都能靈活應對。

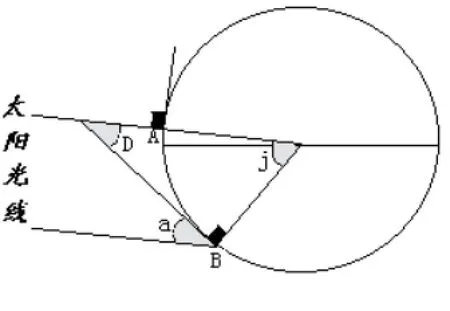
圖2

二、典型題例引發思考，加深理解。

在講課時，為了加深學生的理解，可以用典型問題引發學生的思考。比如讓學生思考理論上北半球夏至日時北極圈和南回歸線兩地正午時分哪一處單位面積上獲得的熱量較多。如果只憑感性，同時由于圖上兩地的正午太陽高度角的確相差較小的緣故，許多學生會匆忙地給出南回歸線上獲得熱量較多的錯誤結論。此時可以讓學生應用正午太陽高度角的計算來具體分析理論上所獲得熱量的大小比較。

北半球夏至日時北極圈66°34°N和直射點23°26°N之間夾角度數為43°08°（66°34°-23°26°），由“九十度減夾角”可得出北極圈此時正午太陽高度角為46°52°；而此時南回歸線23°26°S和直射點23°26°N之間夾角度數為46°52°（23°26°+ 23°26°）；由“九十度減夾角”可得其正午太陽高度角為43°08°。從定量的數值可準確無誤地看出，該日北極圈正午時分單位面積上獲得的熱量相對較多。結合四季變化的內容可以引導學生思考：“北極圈以北地區屬于自然帶五帶中的北寒帶，而南北回歸線間的地區屬于熱帶，而夏至日時北極圈和南回歸線兩地正午時分相比，前者的單位面積上獲得的熱量較多，這說明了什么問題？”通過該問題的分析，四季的形成和正午太陽高度角的計算這兩部分內容都可以得到更為深入的理解。

三、變幻題型、不斷加深，靈活應用。

通過典型題例的分析，學生會對正午太陽高度角計算的實際使用更感興趣了，此時可以趁熱打鐵使用變幻題型進行聯系，從淺到深不斷引導，最終使學生能夠做到舉一反三，靈活應用。具體的導入方式為：

1．先舉直射點與所求點兩點在同一半球的例題讓學生進行計算。比如（10°N，30°N）、（5°N，27°N），學生能很快用“九十度減夾角”得出70°、68°的答案。

2．讓學生解答直射點與所求點兩點在不同半球的例題。比如（10°S，30°N）、（7°S，27°N），也可以用“九十度減夾角”很快得出50°、56°的答案。

3．前兩項混合，使兩點所在半球為隨機出現的例題。

4．分析（20°N，80°S）、（30°N，45°S）等特殊情況。可引導學生發現前者夾角大于90°，出現了極夜現象；后者則出現了直射點所在緯度度數大于了23°26°的錯誤而無法解題。

5．探討已知某一點的正午太陽高度角，求另一點的正午太陽高度角的題目。比如40°N的正午太陽高度角為70°，求45°S的正午太陽高度角。同樣用“九十度減夾角”可以推出直射點與40°N的緯度夾角為20°，則直射點應該在60°N或20°N，舍去虛假的60°N取20°N，就能計算出45°S的正午太陽高度角為25°。

以上例題的數據可以根據課堂具體情況隨時更換，但萬變不離其中，目標在于深入淺出地引導學生掌握正午太陽高度角計算的實質，從而使學生解題時能靈活地加以應用。

綜上所述可以看到，在教學中利用論證求解，并輔以典型和特色題例復習鞏固，能夠較好地引導學生弄清問題的來龍去脈，全面地掌握所學知識。這也有助于培養學生注重思維過程的習慣。有了這一基礎，學生就不再容易受題型變幻的影響，只要把握問題的本質，解決問題起來自然能夠游刃有余。