運動員技能診斷與規劃的灰色理論與方法研究——以高水平田徑運動員專項技能培養為例

孫桂云，王雁玲，劉嘉津，楊森

(寧波大學，浙江 寧波 315211)

目前灰色理論方法在體育領域的應用主要集中在競技體育領域，但多為某些獨立問題的個別研究。從研究整體狀況看，研究缺乏深度，理論不夠系統。因而大大降低了灰色理論方法在體育領域的應用效率，使原本最適合競技體育動態分析和個體化研究的獨特性質沒有得到充分發揮。這里所做的研究就是將灰色理論與田徑專項技能訓練緊密結合起來，運用灰色方法實現田徑專項技能系統的優化，使田徑訓練更具科學性和可控性。

1 研究對象與方法

1.1 研究對象

高水平田徑運動員個體專項技能培養過程中，實施動態量化模型調控的灰色理論與操作方法。

1.2 研究方法

灰色關聯分析、GM(1，1)模型、GM(1，1)殘差模型、GM(2，1)模型、GM(1，2)模型以及灰色系統預測模型方法。

2 結果與分析

2.1 優化方法的整體構造

對于田徑運動員專項技能的系統優化，我們可以從以下幾個方面逐步展開。首先，要了解運動員專項技能可能達到的理想水平，或希望達到的理想水平，即:專項技能發展趨勢預測。這一工作主要目的是大體把握運動員發展潛能和近期目標。然后，對運動員專項技能所涉及的相關指標進行篩選，找出與運動員專項技能密切相關的重點指標，為建立運動員專項技能系統模型做準備。接下來，要對運動員建立包含運動員專項技能重點相關指標的多因素灰色模型，即:建立運動員專項技能及其相關因素指標的模型控制系統。最終，采用指標模型與多因素整體模型相結合的方式，逐一對運動員專項技能指標進行預測，以此對運動員專項技能訓練進行具體的量化指標定位。

2.2 系統優化控制的具體方法

2.2.1 專項技能發展趨勢的預測專項技能發展趨勢可分為兩種，一是從運動員自身發展趨勢出發，預測未來可能的發展潛能;二是從運動員培養任務出發，預測當今運動員所處的環境，以未來整體發展趨勢水平為參照，為運動員設定近期發展目標。由于體育事件包括田徑運動專項技能的發展存在著較強的階段性特征，如運動員運動水平有“起萌”、“上升”、“維持”、“下滑”之分;運動項目的發展可以有“初創”、“發展”、“成熟”，有時還會出現“低谷”等。從預測角度上講，采用不同發展階段的數據，對體育事件的發展趨勢做出預測必然會存在巨大的差異，因而了解體育事件目前所處的發展階段對預測的準確與否至關重要。解決這一問題，從簡便操作方法出發，主要可以采用GM(1，1)模型、GM(1，1)殘差模型和GM(2，1)模型3種方法實現。最基本的方法是GM(1，1)模型方法，但當原始數值擺動偏大時，可以采用GM(1，1)殘差模型加以修正，而當存在明顯轉折事件出現時，則采用GM(2，1)模型方法。我們采集了第14～28屆奧運會女子鉛球的冠軍成績，對其中第14～27屆成績進行分段建模比較分析，并保證所有模型預測值都有實際成績進行驗證。分段的方法是選擇“轉折期”、“轉折前期”和“轉折后期”三段進行 GM(1，1)與GM(2，1)建模對比，具體情況見圖1。

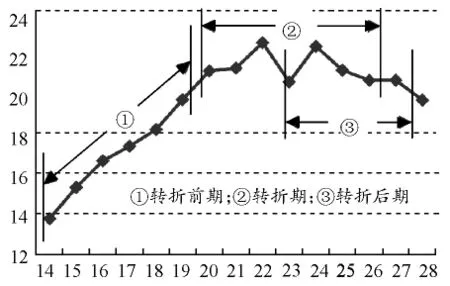
圖1 第14～28屆奧運女子鉛球冠軍成績及分段建模示圖

經計算，得到各段模型見表1。

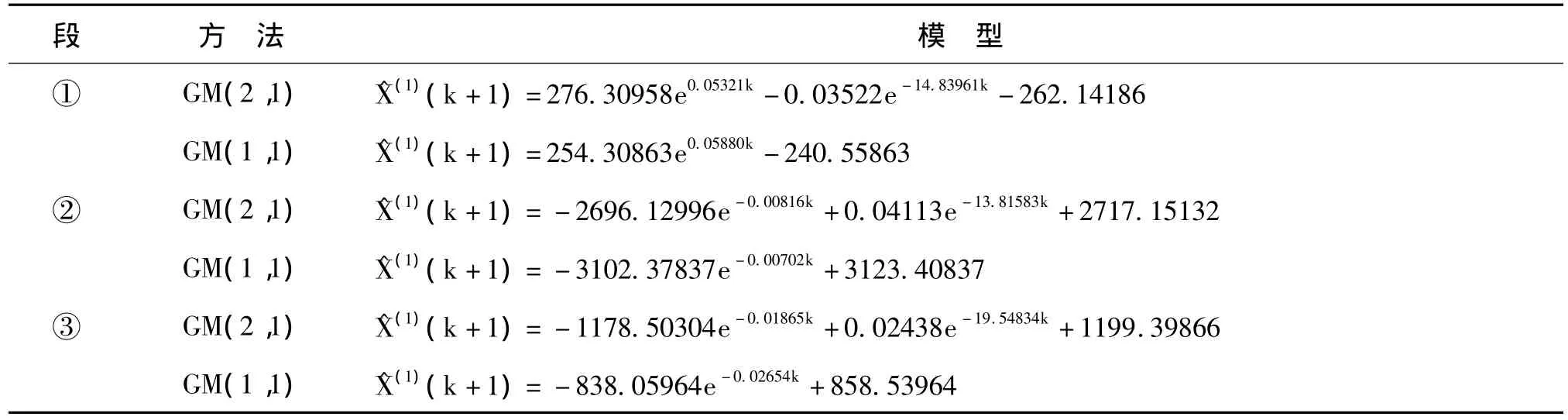
表1 “轉折前期”、“轉折期”和“轉折后期”的GM(2，1)與GM(1，1)模型

對以上模型進行檢驗和與實際值對比分析表明(見表2):

在對相對平滑的數據列進行建模預測時(即:轉折前期)，兩種模型都為一級，但GM(1，1)模型精度更高(C=0.0912明顯小于GM(2，1)的 C=0.1247)，誤差對比也表明，GM(1，1)預測值的誤差為1.76%，而GM(2，1)預測值的誤差要大出3.59倍。因而此時應采用GM(1，1)方法建模預測。

在對具有輕微擺動數據列進行建模預測時(即:轉折后期)，一般情況下，GM(2，1)建模方法不亞于GM(1，1)建模方法。具體問題應視擺動幅度而定，幅度越大越適合采用GM(2，1)方法。

在對有明顯的擺動數據列進行建模預測時(即:轉折期)，GM(1，1)模型的檢驗精度為四級，已無法作為正常的預測模型，只能用GM(2，1)來解決建模問題。此處誤差對比也看出，GM(2，1)的預測結果還是十分理想的。

另外，多年預測實踐經驗提示我們，如果原始數據量較大，采用GM(1，1)還是 GM(2，1)建模預測，可能還不僅僅要考慮數據擺動幅度的大小問題，與轉折期所處的位置也可能有關。一般說，轉折期處在被預測原始數據的前段，往往用GM(1，1)模型可以預測;如果處在被預測原始數據的中段，將不能預測或只能用GM(2，1)模型預測;如果處在被預測原始數據的后段，則多采用GM(1，1)殘差模型預測。

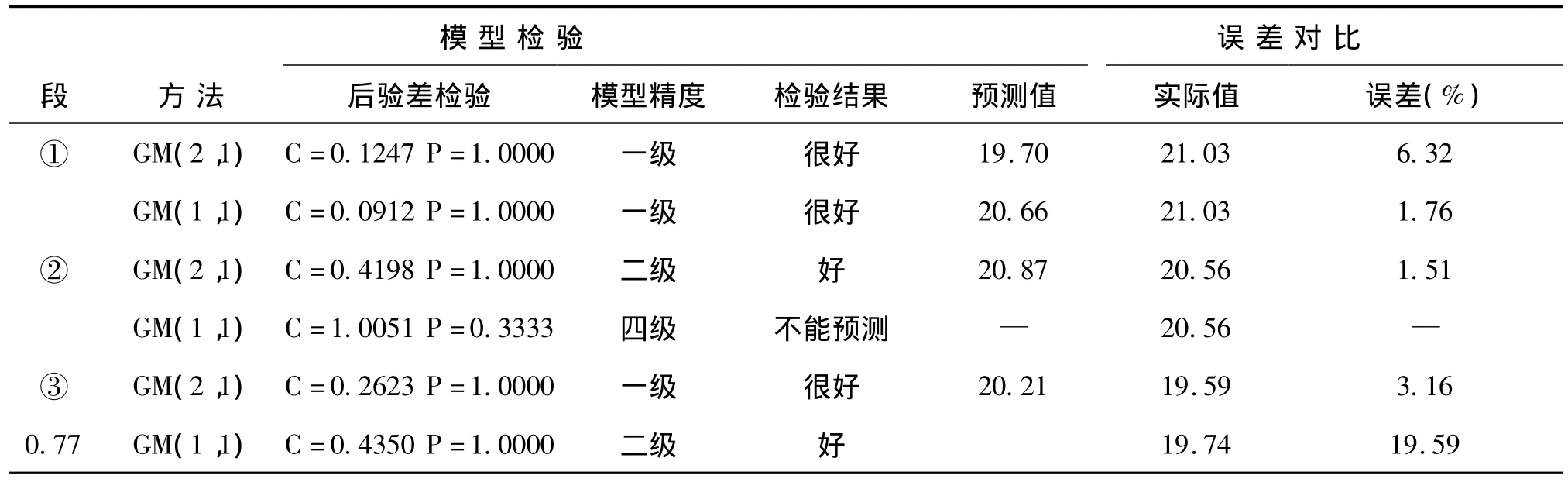
表2 GM(2，1)與GM(1，1)在不同分段情況下的模型精度比較

2.2.2 專項技能重點指標的篩選運動員的專項技能特征主要體現在運動員的各項運動指標上，選擇出合適的運動指標，對運動員進行有針對性的訓練，是當今運動訓練領域實施科學訓練的關鍵。

運用灰色關聯方法對田徑運動員專項運動技能指標進行篩選的最大優勢，就是可以運用運動員技能指標的連續性特征來彌補運動員個體分析數據量少的缺陷，使我們的分析完全適合于運動員的個體特性，而不是眾多運動員的共同特征。

灰色關聯分析的具體方法:［2］(1)建立指標特征值矩陣。(2)對指標進行無量綱化處理。(3)確立指標權重。(4)進行灰色關聯度計算。

以女子鏈球運動員顧原為例(表3)，運動灰色關聯分析方法，篩選其專項技能的重要相關因素指標。

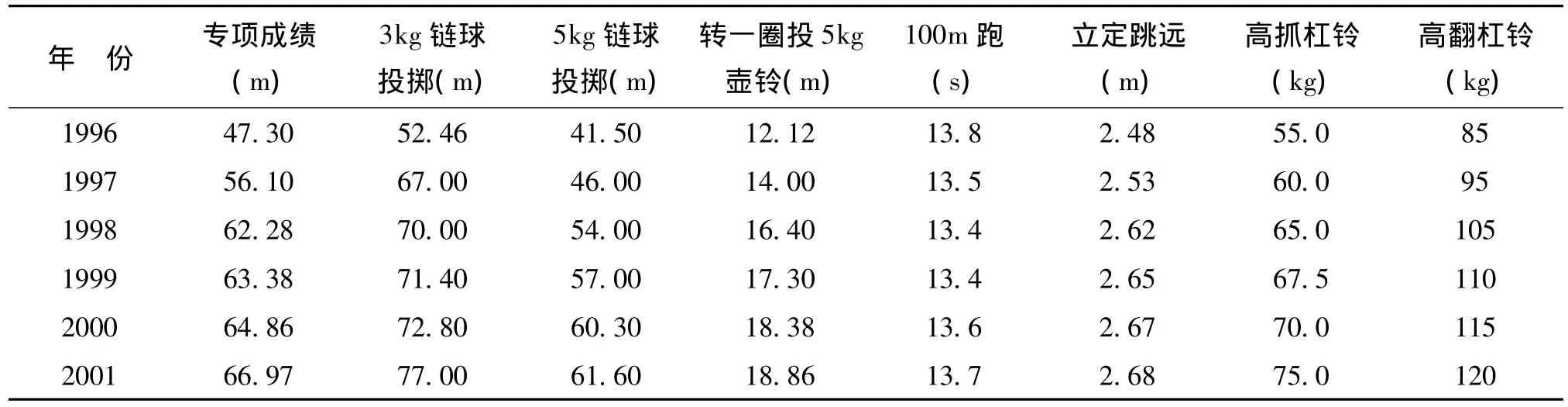
表3 顧原的專項成績與各素質指標關系一覽表［4，5］

由表4我們可以看出顧原專項能力最重要的素質指標為:3kg鏈球投擲、5kg鏈球投擲和高翻杠鈴。

表4 顧原專項成績與各素質指標間的灰色關聯度一覽表

2.2.3 專項技能系統模型的構建專項技能的模型構建主要是建立運動員專項技能的整體系統模型，是用灰色數學方法來反映運動員專項技能的整體構造。

灰色系統預測的具體方法［1－6］:

第一步，確定系統的主導因素和關聯因素，并對各因素間的關系進行定性分析。這一步至關重要，是完成系統預測的基礎。

第二步，建立GM模型群。對系統中的主導因素建立GM(1，1)模型，對關聯因素建立GM(1，h)模型。

第三步，列出系統狀態方程矩陣。

第四步，用龍格—庫塔(Runge2Kntta)法，求解狀態方程。

第五步，對方程解作累減還原，求得系統中各因素的預測值。

以世界紀錄保持者賽布勒十項全能項目為例(表5)。

為減化運算過程，我們又將十項全能各項目分為:速度類、跳躍類、投擲類和耐力類四種素質因素［8］。由于這四種素質因素的發展都具有相對的獨立性，因而我們視其為主導因素，分別建立GM(1，1)模型。而十項全能總分是由以上四種素質因素構成的，我們視其為關聯因素，將建立總分與四種素質因素的 GM(1，h)模型［9］。

我們再將以上所得的模型群轉化為系統狀態矩陣，則有:

首先我們以2003年各因素實際值為參照對模型精度進行驗證(見表6):

表6 塞布勒2003年十項全能水平的系統預測模型值與實際值對比

2.2.4 專項技能訓練指標的定位對田徑運動員專項技能指標建模預測的目的歸結起來，就是要對運動員專項技能指標進行科學定位。也只有實現科學位，才能將灰色理論方法真正運用到運動訓練實踐之中。

實現對運動員專項技能訓練指標的科學定位，需要采用兩種灰色模型，即:GM(n，1)模型和GM(n，h)模型。

GM(n，1)模型為單變量模型，主要特征就是可預測性，即對所研究的變量可以進行超前規劃。但系統中各因素不是孤立的，而單變量模型卻將各因素間的關系隔離開，失去了系統的整體性。要研究系統多因素的整體規劃問題就必須使用多變量模型，即GM(n，h)模型。然而，多變量模型不能直接進行預測研究，要實現系統的超前規劃，就必須將兩種模型結合起來共同完成［10］。

以我國優秀女子跳遠名將關英楠的數據資料為例(表7)，建立GM(n，h)系統狀態基礎模型。

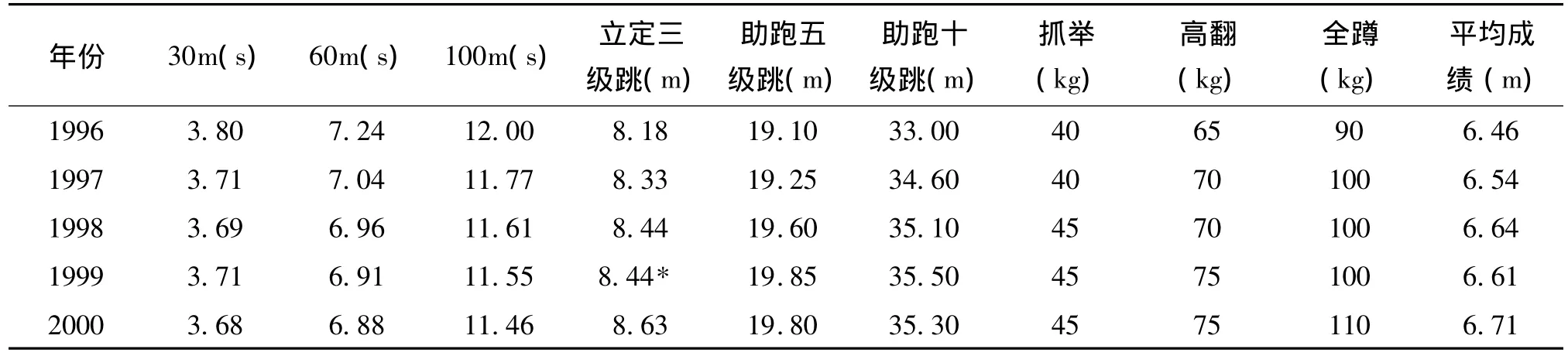
表7 1996～2000年關英楠各項指標成比賽成績

這里我們采用最常用的一次累加方法，即:n=1。再將變量數設定為2，即:h=2。當然我們也可以選擇更多的變量數，但如果我們選擇更多變量參與到模型中來，為使方程有解就必須成倍地增加相應的輔助模型，從而會導致運算量成幾何基數增長。

經計算得出:

檢驗結果:(表8)

表8 9個GM(1，2)模型的關聯度檢驗結果

我們由關英楠近幾年成績可以發現，其年最佳成績間的差距在20cm左右，如果想知道關英楠跳遠超過7.00m時各指標應處的相應水平，就應該首先找出年平均成績超過6.80m的年份。經GM(1，1)預測模型計算，2003年關英楠跳遠的年平均成績將可能達到6.84m，此時的模型維度為8，我們將成績與維度值代入GM(1，2)系統狀態基礎模型中，結果(表9):

表9 關英楠跳遠年平均成績達到6.84m時的各指標相應水平

這樣我們就完成了對運動員專項技能訓練指標的初步定位。

由于灰色模型具備較好的動態規劃特征，我們還可以對運動員專項技能指標做進一步分析和定位。即將各因素指標模型預測值與指標模型規劃值進行進一步對比(見表10):

表10 指標模型規劃值與預測模型值間的對比

由表10發現，按現這樣的發展速度各指標達到相應的目標水平，30m需要14年;60m要3年;100m要3年;立定三級跳要2年;助跑五級跳要3年;助跑十級跳要4年;抓舉、高翻已基本達到該水平;全蹲已超過這一水平。

可見，關英楠的跳遠成績要達到7.00m(年平均成績達到6.80m)，最關鍵的問題是如何提高其助跑的短距離加速能力，按現行的訓練方式很明顯無法達到這一指標，必須在訓練方法、訓練安排上加以改換和側重。

3 結論

灰色系統理論與方法以其貧信息動態性特征，從根本上解決了田徑運動員專項技能系統研究數據量嚴重不足的障礙，真正實現了完全依照運動員個體特征進行專項技能的優化分析和訓練指標的科學規劃。具體可從四個方面逐步展開。

(1)按照當前所處發展階段的不同，選擇GM(1，1)模型方法、GM(2，1)模型方法或 GM(1，1)殘差模型方法建模，實現運動員專項技能趨勢預測和培養目標的科學定位。

(2)采用帶有時間發展特征的灰色關聯分析方法，篩選出運動員專項技能的重點指標。

(3)建立專項技能灰色系統模型，確定運動員個體專項技能的整體狀態。

(4)通過GM(n，1)模型和GM(n，h)模型對比，最終從模型仿真角度計算出訓練實踐所需達到的具體指標數值。

［1］劉思峰，郭天榜，黨耀國，等.灰色系統理論及其應用［M］.北京:科學出版社，1999.

［2］傅立.灰色系統理論及其應用［M］.北京:科學技術出版社，1992.

［3］劉嘉津.解決轉折期體育事件預測問題的GM(2，1)建模方法應用研究［J］.天津體育學院學報，2006，21(3):252－254.

［4］張正紅.我國女子鏈球運動員顧原各項素質和專項成績的關系［J］.湖北體育科技，2001，20(3):27－28.

［5］楊利勇.運用GM(1，N)模型對鏈球運動員顧原訓練狀態的分析研究［J］.山東體育學院學報，2004，20(2):62－64.

［6］肖新平.灰色系統模型方法的研究［D］.武漢:華中理工大學，2002.

［7］http://www.iaaf.2006－03－21/2006－04－27.

［8］盧剛，徐細根.中國與世界十項全能紀錄保持者成績特征對比分析［J］.首都體育學院學報，2005，17(5):76－77.

［9］劉嘉津.體育復雜系統的灰色預測方法探析［J］.中國體育科技，2007，43(1):113－115.

［10］劉嘉津，孫桂云.GM(1，h)系統狀態模型在田徑訓練中的應用［J］.上海體育學院學報，2003，27(1):78－81.

［11］張玉美.關英楠的身體訓練［J］.田徑，2001，(4):12－13.