基于MATLAB仿真的多普勒中心估計算法改進研究

1 引 言

SAR作為現代雷達的一種，已經廣泛應用于軍事及國民經濟等許多領域，如軍事偵察、國土資源管理、環境監測等。多普勒中心頻率fdc的估值是SAR信號處理中的關鍵步驟之一。在SAR成像處理中，fdc估值精確與否直接影響到SAR圖像聚焦和運動補償的精度。有很多學者就fdc估值問題提出了不同的算法[1-3]，頻譜能量均衡法[4]是JOHN等人提出的一種fdc估計算法，也是應用較為廣泛的一種，傳統的能量均衡法在地面場景比較均勻的情況下能得到較好的估值精度，但當地面為非均勻場景時，尤其是場景中有非常強的點目標時，其估值性能急劇下降[5]，這種不足往往因多個距離門作平均處理而表現不明顯，被忽略掉了；能量均衡法的另一個不足是其處理過程中含有迭代運算，很不適合DSP實時處理。文獻[5-6]分別從不同的角度對頻譜能量均衡法作了部分改進，文獻[6]提到通過能量中心均衡逼近以及距離加權擬合來改進傳統的能量均衡法；文獻[5]則更多地考慮算法結果的精確性。本文從如何提高實時處理效率角度出發，通過更為簡潔的算法避免了迭代運算，而且當回波中有強點目標時，通過刪除異值的方法使估值結果更為準確，文章最后應用MATLAB語言進行了多普勒中心估計新算法的仿真，并給出了實際的成像應用成果。

2 SAR工作原理

SAR 的方位向和距離向的高分辨率都是通過對Chirp信號的壓縮得到的，但是Chirp信號產生方式不同。雷達系統發射Chirp信號代替單頻的雷達脈沖，并對接收到的回波信號進行脈沖壓縮可以得到距離向的高分辨率。而在方位向上則利用了回波的方位相位調制，這種調制是由于在雷達運動過程中目標與雷達之間的距離隨時間變化引起的。回波信號因多普勒效應而產生了近似于線性調頻脈沖的信號，處理機將這一調制信號進行壓縮，從而在寬波束天線上得到與窄波束天線相同的分辨率。為此，必須積累連續位置上的雷達回波才能進行SAR信號處理，這是其區別于其他成像雷達的主要特征，也是SAR技術的關鍵所在。

圖1是載機和地面目標之間的基本幾何關系。P為處于雷達波束照射下的點目標，圖中參數φ為載機在O點(t=0)時向量OP與速度向量之間的夾角；h為載機飛行高度；v為載機速度；r為點目標P和載機的距離；rc為點目標P和載機的最短距離；R為載機在O點(t=0)時同點目標P之間的距離。

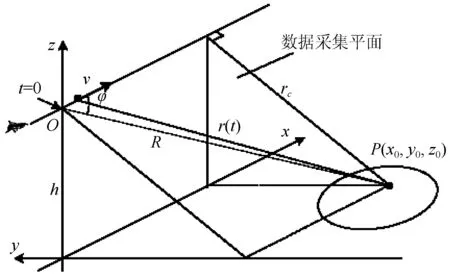
圖1 載機與地面目標幾何關系

根據圖標的幾何關系，雷達和點目標的距離函數為：

(1)

假設脈沖寬度為Tp，調頻率為kr，雷達發射的脈沖線性調頻信號的形式為：

(2)

則經過雷達波束照射區域內點目標P反射并去載頻后，雷達接收到的回波信號為：

·

(3)

式中，Ta為合成孔徑積累時間，c為光速，λ為工作波長。

對式(3)所示的回波信號的方位相位φ(t)=-4πr(t)/λ求導可以得到方位向瞬時頻率：

fa(t)=fdc+frt|t|≤Ta/2

(4)

通常把它稱為點目標回波的多普勒頻率歷史，簡稱多普勒歷史。由其表達式可以看出，多普勒歷史是一個按照負斜率變化的線性調頻信號，其調頻斜率(即方位向調頻率)fr為：

(5)

多普勒中心頻率為：

(6)

在SAR成像處理中，fdc估值的準確度非常重要，估值不準確將導致信噪比降低，方位模糊度增加，輸出圖像會發生位置偏移，影響SAR圖像定位[7]。

3 頻譜能量均衡法

由于點目標的SAR回波信號在方位向是線性調頻信號，其瞬時頻率和孔徑時間存在線性關系。因此，在理想飛行情況下，方位向回波某個頻率上的能量必然來自于雷達照射區域中某個特定方向上的目標。在假定照射區域為均勻場景(各點目標具有相同的散射特性和散射截面積)情況下，回波的方位向功率譜密度顯然與雷達天線方向圖有著相同的形狀。通常情況下，天線方向圖都是相對于波束中心對稱的，因此，回波方位向功率譜密度也是對稱的，其中心對稱點即為多普勒中心。

由于點目標的方位譜是以多普勒中心頻率fdc為中心對稱，因而為方位譜的能量中心代替多普勒中心帶來可能，這就是頻譜能量均衡法。圖2為該方法的流程圖。

以下是傳統的頻譜能量均衡法具體操作步驟說明：

1) 根據SAR系統參數和慣導數據，得到多普勒中心頻率的初值fDC;

2) 經過距離脈沖壓縮處理，將回波信號轉換到距離—多普勒域，產生方位譜信號；

3) 根據fDC將頻譜搬移至零中頻；

4) 計算零中頻兩側方位譜的能量E1和E2；

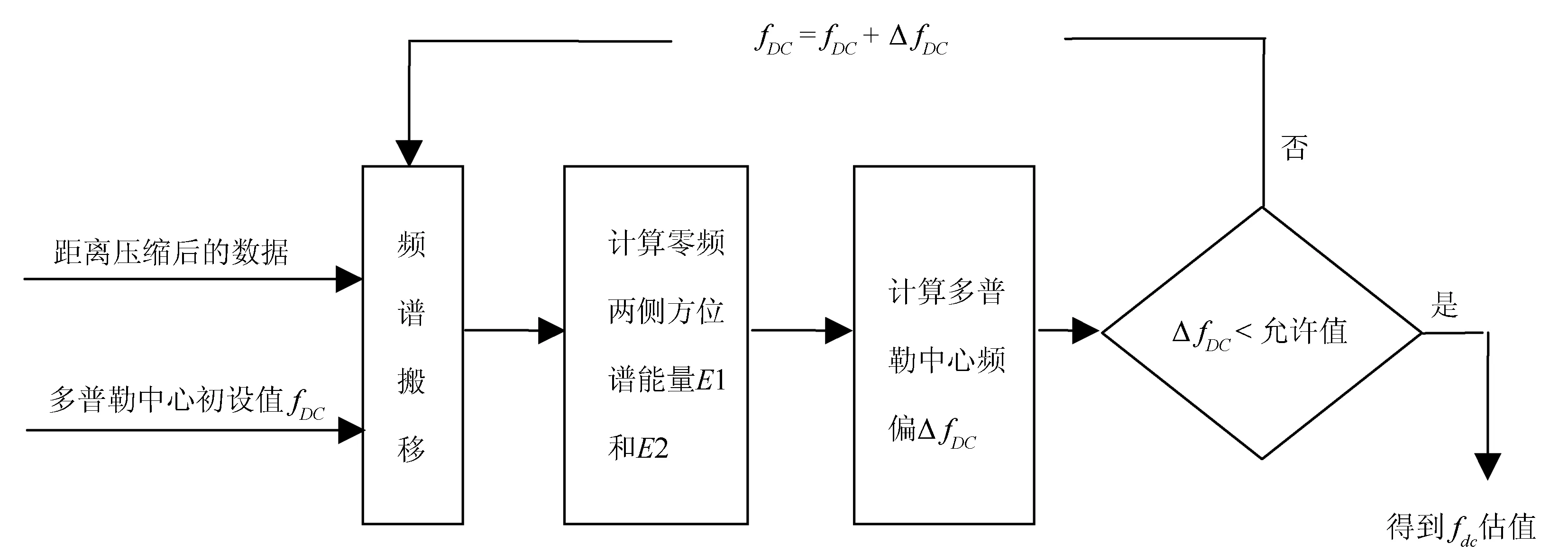
圖2 頻譜能量均衡法流程圖

5) 計算此時的能量中心的估計值偏差ΔE=E1-E2;

6) 判斷ΔE是否在允許的誤差范圍內，以便決定是否迭代，如果在允許誤差范圍內，則得到了fdc估值，否則fDC=fDC+ΔfDC并從步驟3)開始重復。

該方法由于存在迭代運算，因此不適合DSP實時處理，算法效率不高。

在實際應用中，當地面散射特性比較均勻時，回波譜對稱性好，多普勒中心頻率估計比較準確，但當場景不均勻時，尤其是存在強點目標時，該方法估值精度會下降很多。如圖3所示，該圖表現的是一段含有強點目標的方位向頻譜，真實的多普勒中心應該在A點，但由于譜峰值B點處能量很強，如果用能量均衡法，則會將多普勒中心誤判為B點或B點附近，使多普勒中心估計不準確，該點也就是我們所謂的頻譜能量均衡法中需要注意的奇異點。若將頻譜中該奇異點刪除(如圖4所示為將B點幅度賦零后的頻譜圖)，再通過能量均衡法估算fdc，就比較準確了。

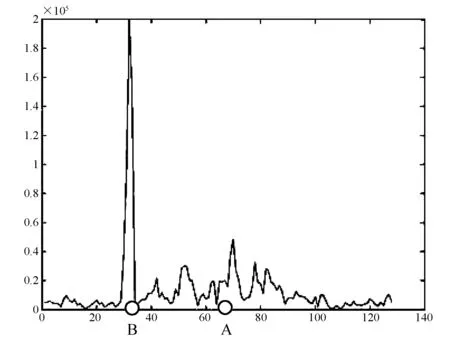
圖3 去異值前的頻譜

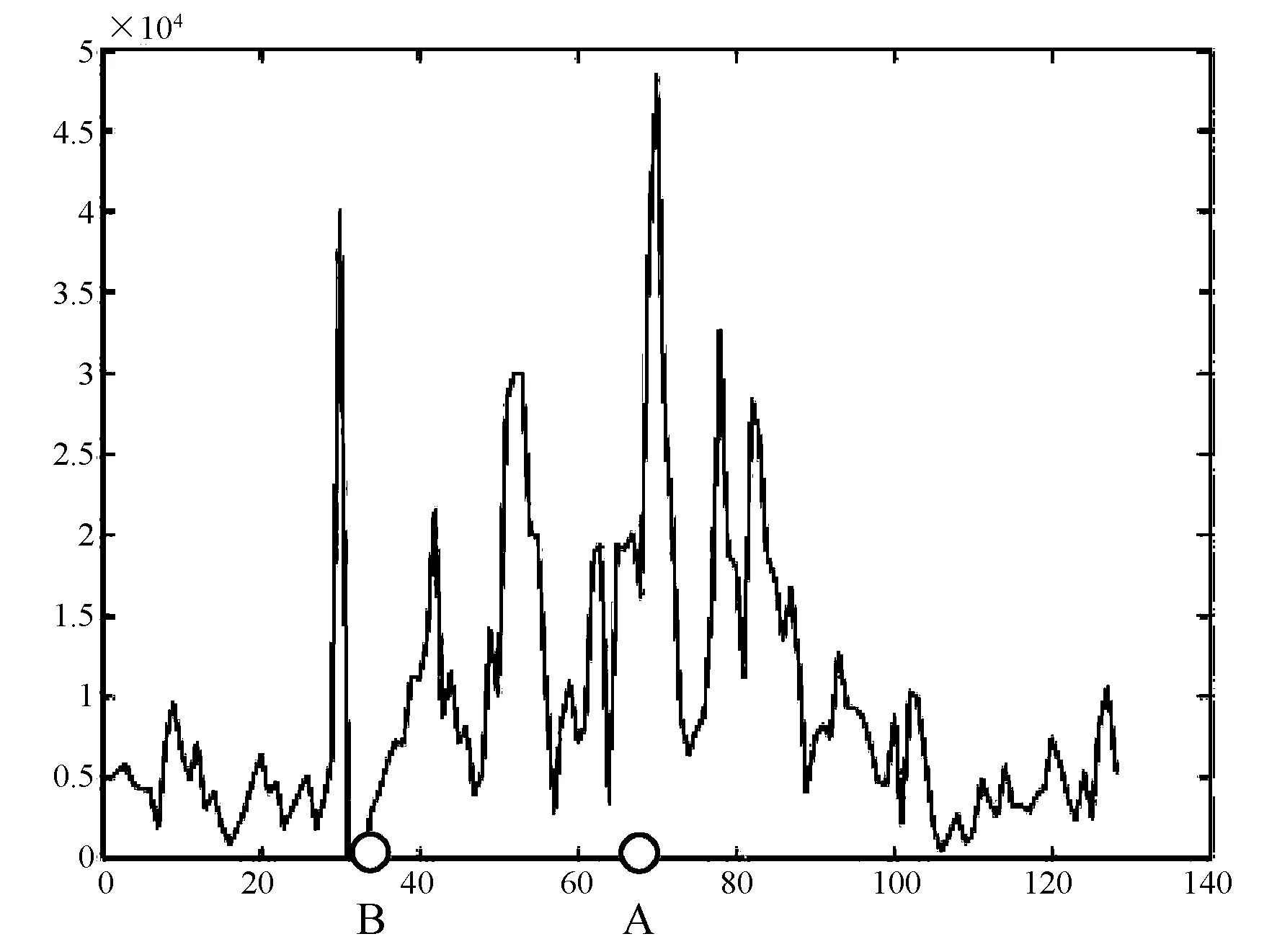
圖4 去異值后的頻譜

4 能量均衡法的改進

上一節已經提到傳統能量均衡法的一些不足，即存在迭代運算和在含強目標場景下估值不準的問題，新的方法主要在這兩點上進行了改進。在頻域上，對于強點目標回波，其幅度一定遠遠高于頻譜能量均值，因此可以設定一個門限，將這些奇異值刪去，即做賦零處理。

而對于迭代運算的簡化處理，我們可這樣考慮，在刪除異值后，方位譜的包絡大致近似于雷達天線方向圖，能量中心點C′大約在頻譜峰值點附近。我們可先找到峰值點，再通過加權處理的方式求得加權能量中心點C′的偏移量，這樣就可得到加權能量中心點C′，當然這個C′并不等同于絕對的能量中心點C，但它是能量中心點C的一個估計值，而且估計誤差較小，完全在容忍誤差范圍之內。在第5節中將列出由SAR原始數據處理得到的結果及其分析。

算法框圖如下：

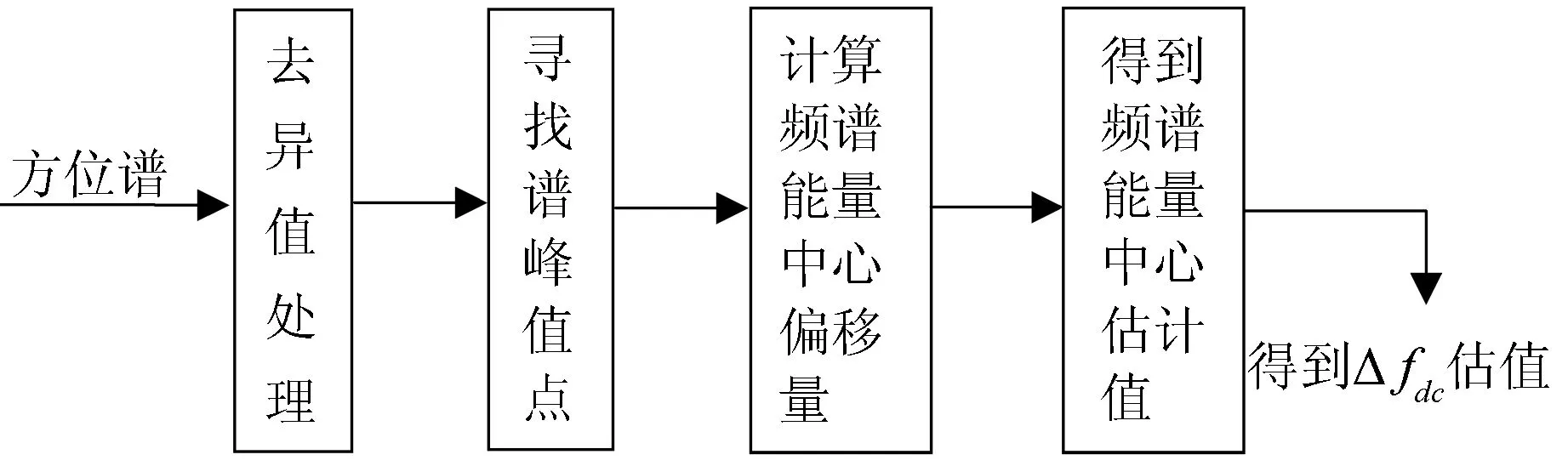
圖5 改進的頻譜能量均衡法流程圖

以下是該算法具體操作步驟：

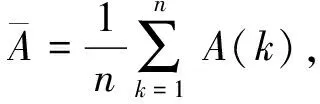
2) 尋找頻譜峰值點p點，該頻點幅度為A(p)；

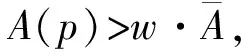
4) 令第k頻點加權值為g(k):

(7)

5) 求出加權頻譜能量中心偏移量:

(8)

6) 求出頻譜能量中心估計值C=p+Δf，該能量中心C所對應的頻點值即為fdc估計值。

舉例說明：當方位譜為128點傅立葉譜，首先刪除掉異值點，得到刪除了異值點后的譜，并找到這個新的譜的峰值點p點，假設p=110，即110頻點。由公式(7)得到110頻點加權值為0，109和111頻點加權值分別對應-1、+1，依此類推，每個頻點都對應著一個加權值g(k)(g(k)∈=[-63,64])，根據公式(8)得到加權頻譜能量中心偏移量Δf，能量譜中心估計值為C=p+Δf，即fdc的估計值。

5 仿真實驗及實測結果分析

5.1 仿真實驗及結果分析

筆者通過MATLAB語言對該算法進行了仿真。首先構建了一個環境模型，環境參數如表1所示。

表1 仿真實驗環境參數

雷達天線工作在掃描模式，因此不同的天線角度指向對應著不同的多普勒質心頻率fdc，這種工作模式也非常適合分析驗證fdc估值算法。

由參數可知，天線從72°～108°為半周掃描，共耗時2 s，即4 000個重頻。我們對數據進行如下處理：首先在距離向做脈沖壓縮處理；繼而將方位向數據按128個重頻劃分作為一個相干處理單元CPI，則半周掃描(72°～108°)可劃分為31.25個CPI，為方便計算，取32個CPI的數據處理，每一個CPI的數據在方位向做FFT相干積累后，用改進的能量均衡法估算fdc值(距離向每128個距離門做均值處理)。

圖6(a)反映的是用新算法求解的連續32個解模糊之前的值，圖6(b)反映的是解模糊之后的fdc值，圖6(c)是環境模型中輸入的天線掃描情況。通過比較圖6(b)和圖6(c)可看出天線來回掃描，從正速度到零速，再到負速度，32個fdc值求解得比較精確。

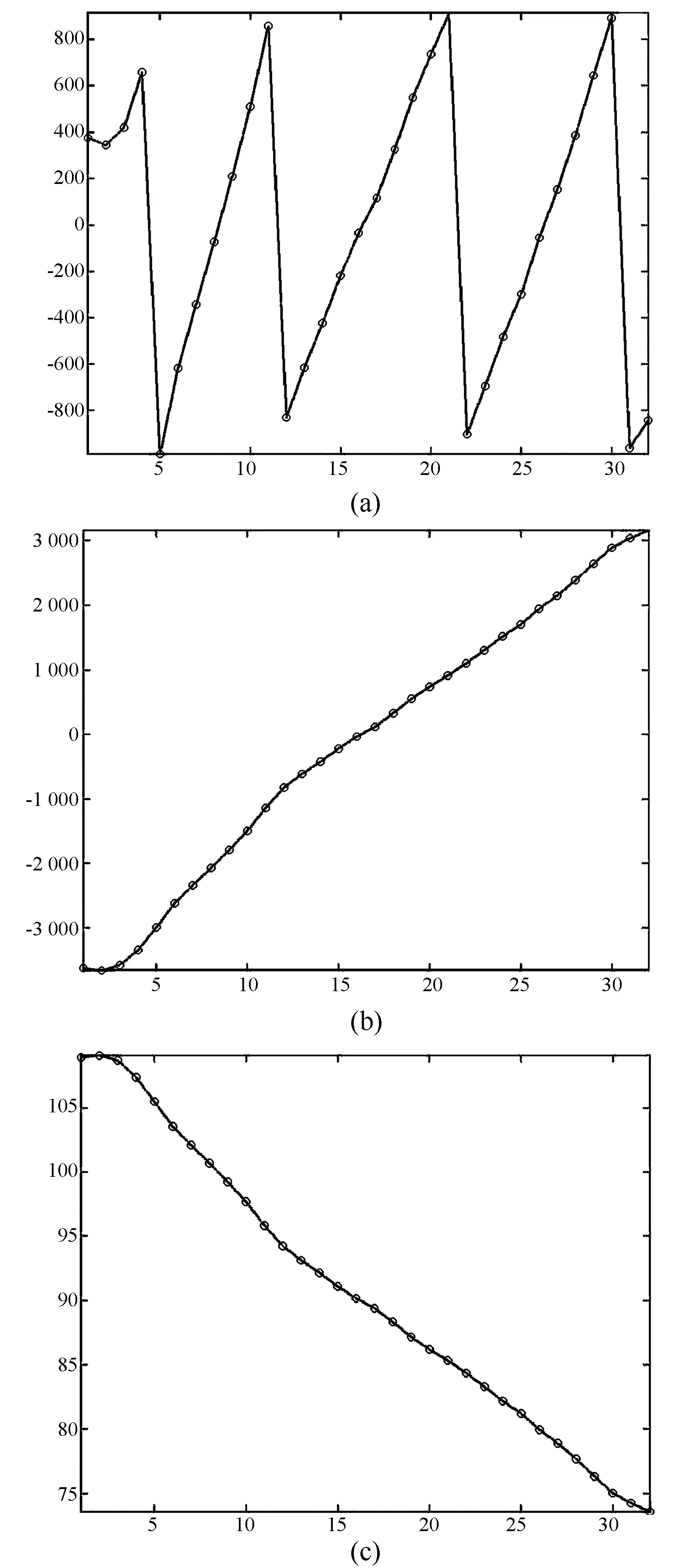
圖6 天線掃描波束指向及對應的多普勒頻率圖

5.2 實測結果分析

我們選取某型雷達所測的一段實測數據，并選取均勻場景，一般非均勻場景2種類型數據，每一種場景數據考察3例，通過時域相關法、頻譜能量均衡法和改進的頻譜能量均衡法得到如表2、表3的對比結果(表2，表3中方法1表示時域相關法，方法2表示頻譜能量均衡法，方法3表示改進的頻譜能量均衡法)。

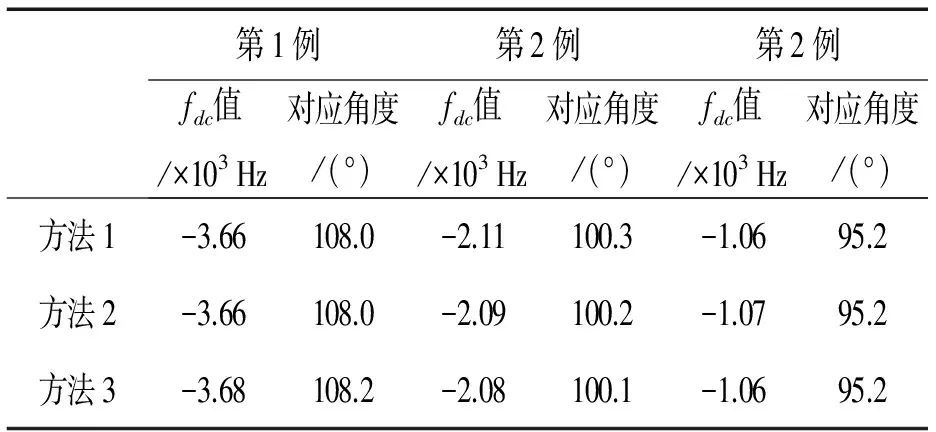
表2 均勻場景下各種fdc估值方法結果比較

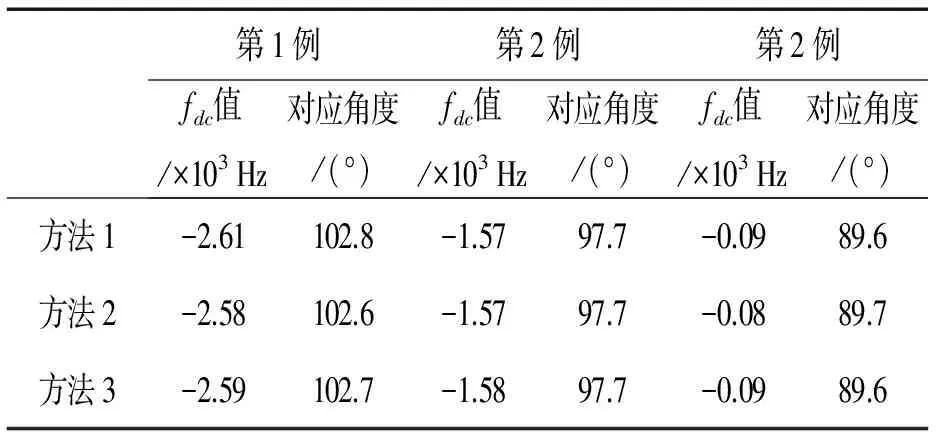
表3 非均勻場景下各種fdc估值方法結果比較

由處理結果可看出，改進的能量均衡法與傳統的能量均衡法和時域相關法等方法相比，多普勒中心估值結果相差不大。但由于新方法避免了迭代運算，計算速度提高了。

6 結 論

多普勒質心估計一直是SAR信號處理中的關鍵步驟之一，傳統的頻譜能量均衡法是一種較為經典的多普勒質心估算方法，但當場景中存在強點目標時，利用該方法得出的估算值不夠準確，而且由于該算法存在迭代運算，也不利于DSP實時處理。改進的能量均衡法較好地解決了這個問題，文章最后給出了MATLAB仿真和實測數據得到的結果，并給出了比較分析結論。

[1] LI F K. Doppler parameter estimation for spaceborne synthetic-apertrue radars[J]. IEEE Trans. GRS, 1985,23(1): 47-55.

[2] JIN M Y, et al.Optional Doppler centroid estimation for SAR data from a quasi-homogeneous source[J]. IEEE Trans. GRS,1986,24(6): 1022-1027.

[3] MADSEN S N, et al.Estimating the Doppler centroid of SAR data[J]. IEEE Trans. AES,1989,25(2): 134-140.

[4] JOHN C C, et al.Synthetic aperture radar system and signal processing[M]. John Wiley & Sons, INC., 1991.

[5] 孫泓波，顧紅，等.機載雷達成像中的兩種改進多普勒質心估計算法[J].兵工學報，2002，23(1)：49-53.

[6] 劉國慶，黃順吉.星載SAR多普勒質心估計的改進方法[J].信號處理，1994，10(3)：156-160.

[7] 魏鐘銓.合成孔徑雷達衛星[M].北京：科學出版社, 2001．