結合均值導納法的聲吶腔自噪聲統計能量分析

1 引 言

統計能量分析方法(SEA)的核心是統計能量分析參數(模態密度、耦合損耗因子以及內損耗因子)的確定。一直以來，耦合損耗因子的計算都是依賴于以保守弱耦合為基礎的經驗公式。在復雜結構聲和振動響應預測中的應用受到限制。利用均值導納法預測結構間的振動響應可以克服經典統計能量分析關于模態密度和弱耦合假設引起的缺陷，從而擴大統計能量分析法的應用范圍，提高統計能量分析的預測精度。

孫進才[1-3]等人在這方面做了大量的工作，利用均值導納法推導了點連接結構、線連接結構耦合損耗因子的計算公式。本文在此基礎上，利用均值導納法推導湍流邊界層激勵下復雜結構—聲耦合系統——板—柱殼—板—聲吶腔的耦合損耗因子，預測聲吶腔的自噪聲。

2 聲吶罩統計能量分析模型

俞孟薩[4，5]等人對均勻湍流邊界層激勵聲吶罩模型進行了分析。本文采用的聲吶罩模型為兩端封閉的圓柱殼模型。圓柱殼半徑為R，長為L，厚度為hs，兩端圓形封板半徑為R，厚度為hp，兩者密度均為ρ。相應的統計能量分析模型如圖1所示。此模型的能量平衡方程為：

(1)

式中，ηit=ηi1+ηi2+ηi3(i=1,2,3)。

確定了所有的參數后，根據式(1)求出E2，再根據下式即可計算得到聲吶腔的自噪聲：

(2)

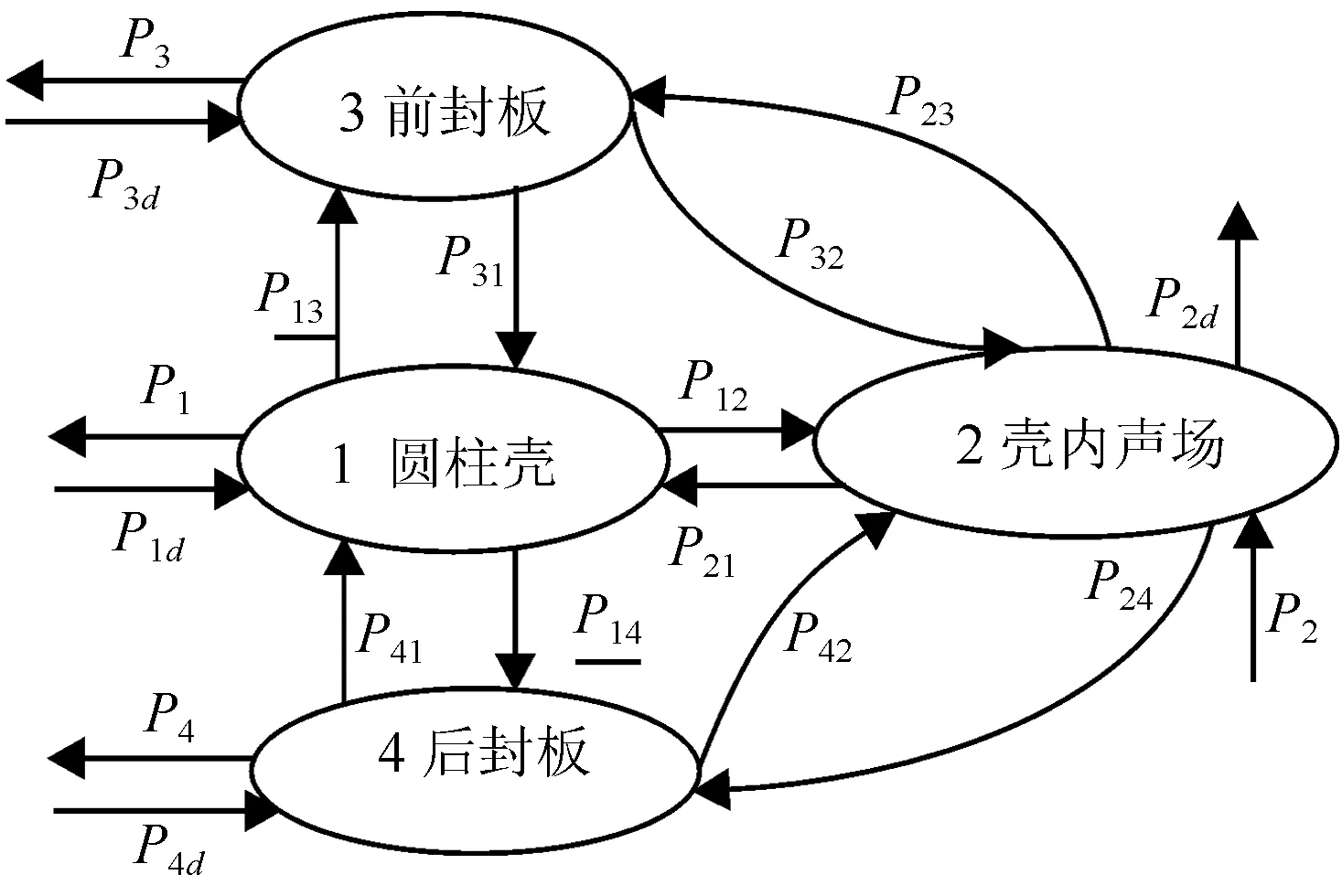
圖1 聲吶罩統計能量分析模型

式中，pi、ρ0、C0、Vi分別為聲子系統均方根聲壓、介質密度、聲速、體積。

3 統計能量分析參數的確定

1) 模態密度

柱殼的環頻率為：

fr=Cl/(2πR)

(3)

式中，Cl為柱殼材料中的縱波速。

柱殼的模態密度為[5]：

(4)

式中，A為圓柱殼表面積。

殼內聲場的模態密度[5]近似計算公式為：

(5)

式中，V0為聲場的體積；Aa為聲場的表面積。

圓板的彎曲模態密度為：

n4(ω)=0.5Ap(m/D)0.5=n3(ω)

(6)

式中，Ap=πR2為板的面積；m=ρhp為板面密度；D為板彎曲剛度。彈性殼體在受流體負載作用后，其模態頻率會向低頻移動，相應的模態密度也會產生變化。Blake給出了有流體負載的平板的模態密度，其表達式為：

n4(ω)=0.5A3(mL/D)0.5/a

(7)

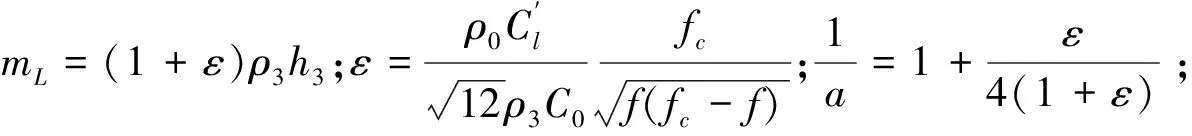
2) 內損耗因子

根據文獻[6]，組合結構中1個結構子系統的內損耗因子是由3個部分組成的：結構損耗因子、連接邊界損耗因子、聲輻射損耗因子。在給定頻率，結構損耗因子僅與材料有關。結構損耗因子的數量級為10-3～10-4。連接邊界損耗因子則與連接的形式有關。連接形式的不同而導致的聲壓級的差異通常在0～3 dB。因此，此處不具體計算連接邊界損耗因子，而是在最終的聲壓級計算結果上加上修正值。結構的聲輻射為雙面聲輻射。因此有：

η1=η1s+η1r,η3=η3s+η3r,η4=η4s+η4r

(8)

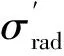
聲場的內損耗因子可從聲場的混響時間T60得到[6]：

(9)

式中α,Af分別為非透聲界面的吸聲系數、非透聲界面的面積。

3) 耦合損耗因子

本文利用均值導納法計算圓板—柱—圓板耦合損耗因子。其計算矩陣如下：

(10)

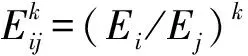
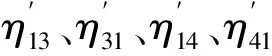
(11)

式中，Y1、Y4、Y3分別為子系統1、3、4的平均輸入導納，y1、y3分別為子系統1、3的平均傳遞導納。且據文獻[7]有：

(12)

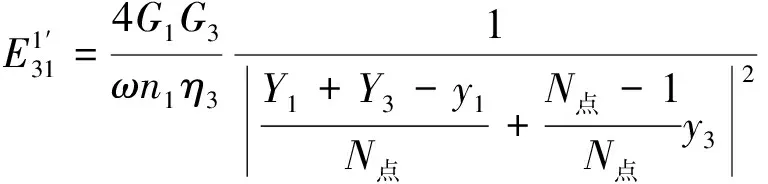
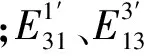
利用式(12)求得經典耦合損耗因子，然后代入式(11)求得振動能量比，將所得各數值代入式(10)中，即可得結構子系統間的直接耦合損耗因子和間接耦合損耗因子。

4) 輸入功率

聲吶罩一般為水翼截面的柱殼，本文為便于討論采用圓截面柱殼。僅圓柱殼均受到湍流邊界層脈動壓力激勵。湍流邊界層脈動壓力為空間分布的隨機力。如圖2所示，平行于組合結構對稱軸的無窮遠處均勻來流流經結構表面，在結構表面形成湍流邊界層。

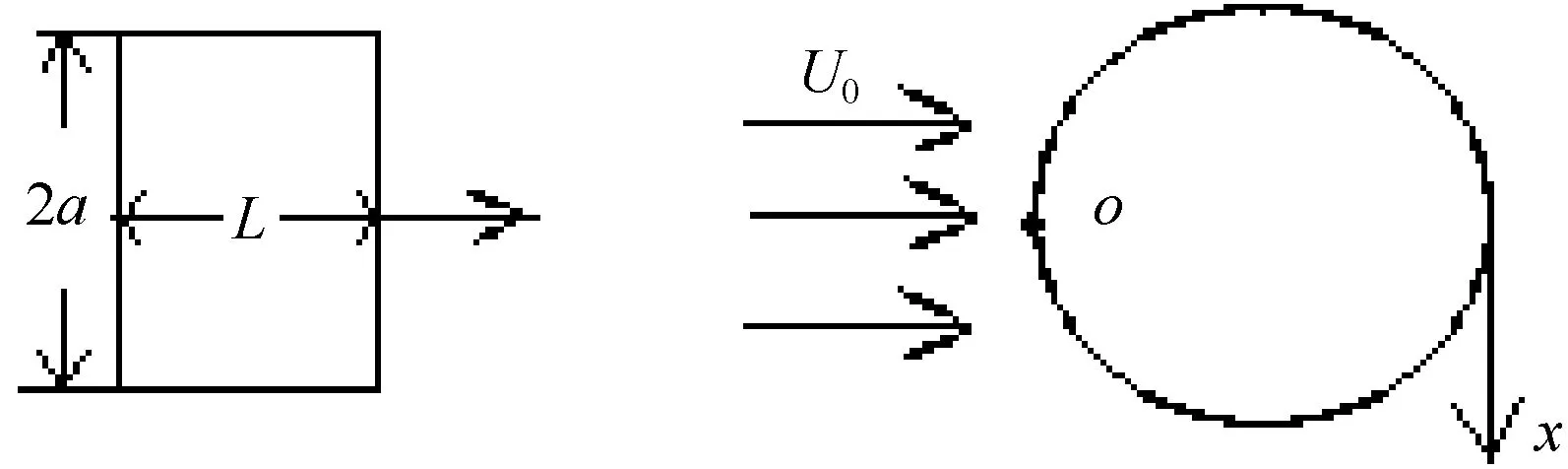
圖2 聲吶罩物理模型

柱殼表面兩點X(x1,θ1)、X′(x2,θ2)。利用導納法計算輸入功率。Han研究了導納與輸入功率的關系。稍做推導，得出均布隨機脈動壓力對柱殼的輸入功率的計算公式：

ds

(13)

式中，Sxx′(ω)為柱殼表面壓力互譜密度函數；Mpxx′*(ω)為柱殼的傳遞導納函數Mpxx′(ω)的共軛；s1為柱殼的面積。

SXX′=φpp(ω)e-γ1|ωα1/Uc|e-γ2|ωα2/Uc|e-jωα1/Uc

f0=U0/(3.68δ),δ=0.37L(U0L/ν)-0.2

(14)

式中，φpp(ω)為脈動壓力的自功率譜密度，γ1、γ2為周向和軸向的衰減因子；α1、α2為X、X′兩點周向和軸向的距離；Uc為外部流體的對流速度；L為所考慮位置至回轉體頂端距離。對于未分離的湍流邊界層，這些參數的取值如下：

Uc=0.65U0,γ1=0.32,γ2=0.7

文獻[8]中推導了圓柱殼的傳遞導納函數：

MpXX′(ω)=M10(ω)(Π(Kr)+Π(Kr′))

(15)

式中，M10(ω)為柱殼的輸入點導納，文獻[8]中也給出了計算公式；Π(Kr)為柱殼傳播函數，Π(Kr′)為繞柱殼一周后到達被激勵點的響應。它們為第二類零階Hankel函數之差：

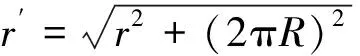
圓板和內部聲場由于沒有外部激勵，因此：

P2=P3=P4=0

4 計算分析

根據前面建立的計算模型計算給定參數下的聲吶腔自噪聲。本文柱殼、圓板都選用不銹鋼材料。相關幾何參數以及外部流場參數見表1。

表1 計算參數

圖3為用波動法、均值導納法計算得到柱殼到圓板的直接耦合損耗因子的比較。均值導納法比波動法的計算簡便。柱殼到圓板的直接耦合損耗因子的波動法的計算值根據文獻[9]中給出的公式進行計算。從圖中可以看出，波動法、均值導納法兩者能給出基本一致的結果。這與文獻[9]中的結論一致。圖4為湍流邊界層柱殼的輸入功率的圖譜。圖5為聲吶腔的自噪聲聲壓級圖譜。

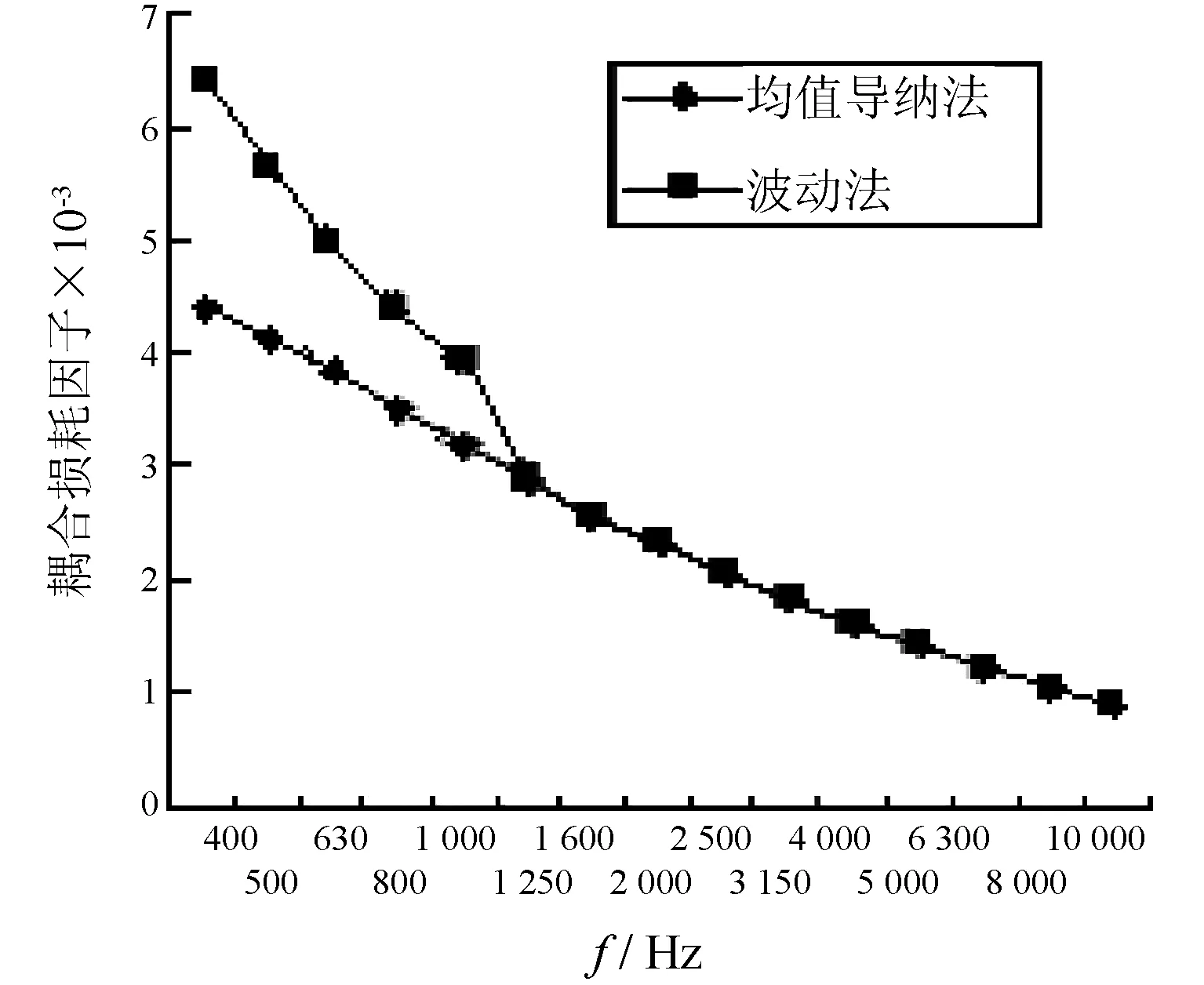
圖3 模型一柱殼到圓板的CLF的比較

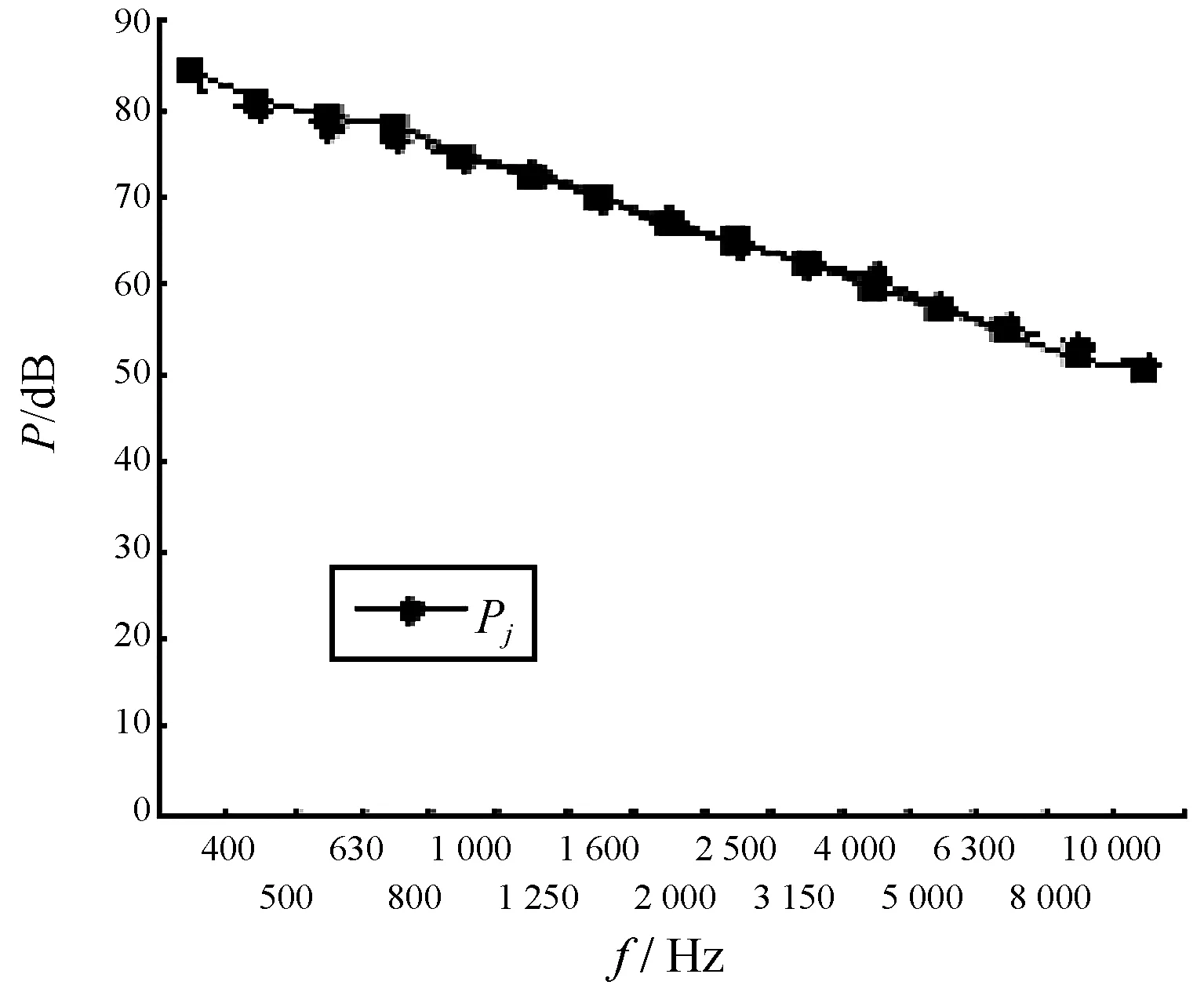
圖4 湍流邊界層對柱殼的輸入功率級

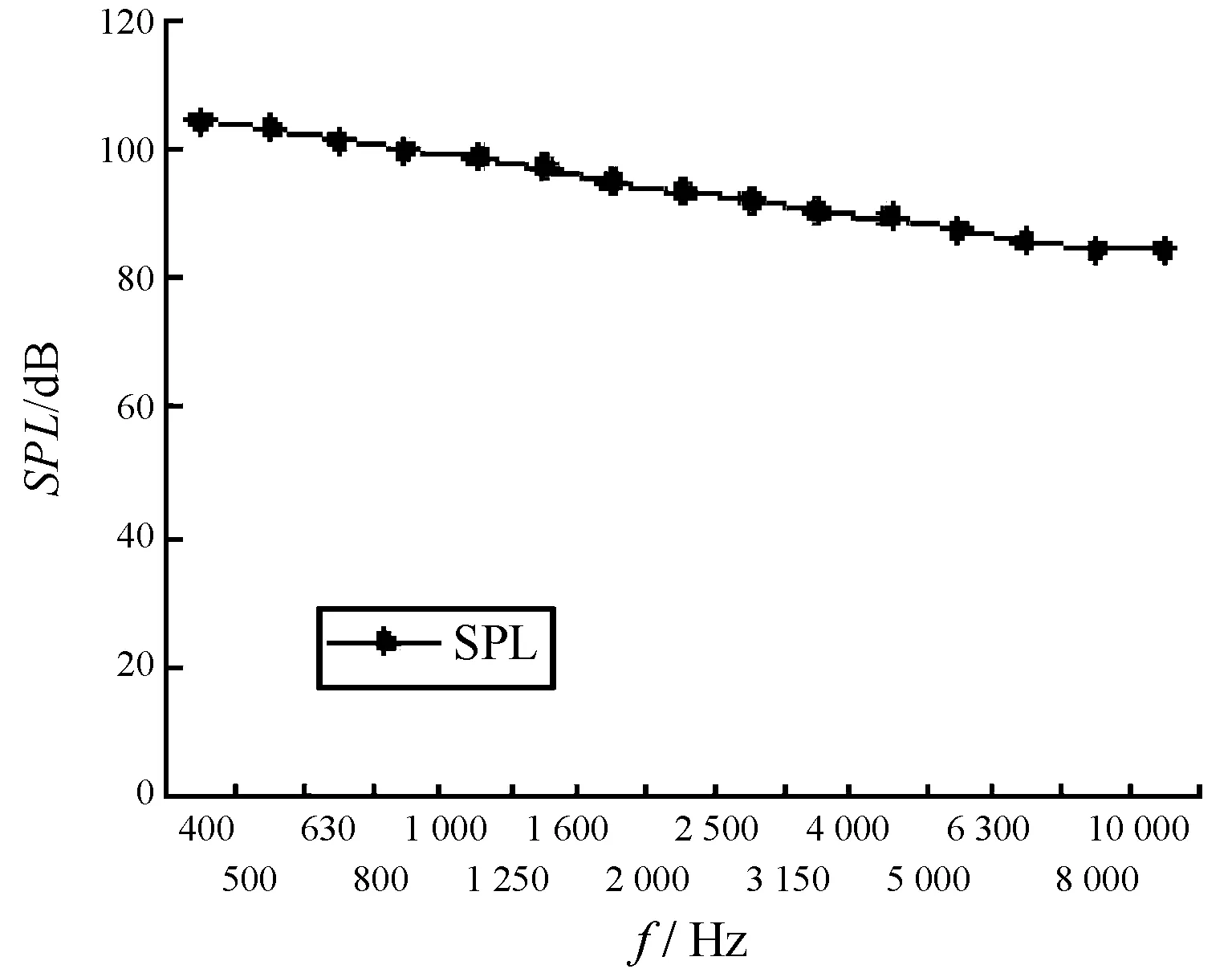
圖5 聲吶腔自噪聲聲壓級

圖3～圖6中橫坐標的頻率為1/3倍頻程中心頻率，圖4中縱坐標為功率級，基準值Po=10-12W，圖5中聲壓級的基準值為10-6Pa。

為了更好地比較波動法與均值導納法計算耦合損耗因子的結果，此處再給出一個算例。參數如下：半徑R=1 m，L1=2 m，外部流場參數與上相同。柱殼到圓板的直接耦合損耗因子計算結果比較如圖6。圖6的結果比較更進一步地說明了波動法與均值導納法在計算耦合損耗因子上的一致性。

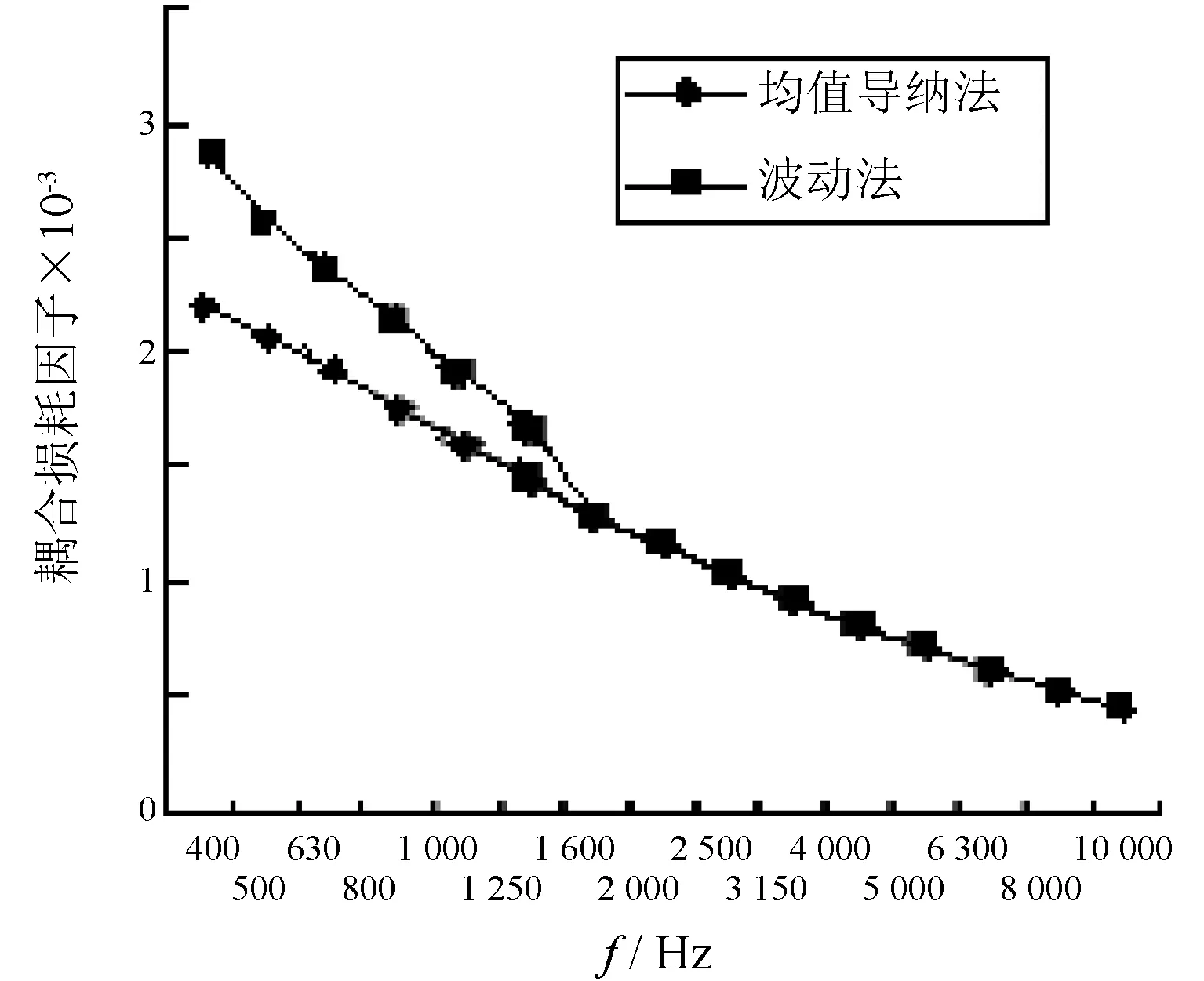
圖6 模型二柱殼到圓板的CLF的比較

5 結 語

本文著重介紹了利用均值導納法計算耦合損耗因子，計算過程中利用到了經典統計能量分析參數，并與利用波動法得到的耦合損耗因子的值進行了比較，兩者基本相同。另外，計算了復雜結構湍流邊界層的輸入功率，推導出了沿柱殼對稱軸方向均勻來流對柱殼的輸入功率的表達式。給出了一具體的算例，計算結果與有關文獻結果相符。實際的聲吶罩罩壁多為正交異性材料玻璃鋼，對于正交異性材料殼的SEA參數的計算還在研究當中，也是以后統計能量分析研究的重點。

[1] 盛美萍，孫進才，王敏慶，等.直接和間接耦合損耗因子的計算方法[J].噪聲與振動控制，1997(6)：1-6.

[2] 盛美萍，王敏慶，孫進才.多點連接結構振動響應的均值導納法預測[J].西北工業大學學報，1999，17(2)：171-175.

[3] 張娟，李天勻，劉敬喜，等.空間不均勻湍流邊界層激勵下聲吶腔自噪聲統計能量分析[J].中國艦船研究，2007，2(6)：24-29.

[4] 俞孟薩，葉劍平，等.船舶聲吶部位自噪聲的預報及其控制技術[J].船舶力學，2002，6(5)：80-94.

[5] 俞孟薩，李東升.統計能量法計算聲吶自噪聲的水動力噪聲分量[J].船舶力學，2004，8(1)：99-105.

[6] 姚德源，王其政.統計能量分析原理及其應用[M].北京：北京理工大學出版社，1995.

[7] 錢斌，楊世興，盛美萍，孫進才.封閉圓柱殼的振動響應特性研究[J].機械科學與技術，2002，21(1)：122-126.

[8] 錢斌，汪源源，盛美萍,等.距離對板殼結構傳遞點導納得影響[J].西北工業大學學報，2005，23(2)：156-160.

[9] 楊曉華，姚德源.有限長圓筒殼與圓板連接的耦合損耗因子研究[J].戰術導彈技術，2002，3(2)：34-37.