典型艦船艙室大氣環境仿真
1 引 言
目前在艦船艙室大氣環境設計中,安裝有大功率發熱設備和動力設備的重要艙室由于設備布置密集,在通風調節的過程中,極可能形成局部區域溫度、壓力梯度較大等設計不足,從而造成局部通風效果較差,不能達到所要求的艙內大氣環境。為解決以上設計中出現的問題,傳統的射流理論可以簡單、快捷地預測機械通風室內沿射流方向各個位置的速度或溫度分布,從而了解室內空氣分布情況。但是用射流公式預測室內空氣分布有很大的局限性,依賴于確定射流公式的經驗參數。另外,射流公式揭示的多為射流主體段的流動特性,對于送風口相對空間尺寸較大、送風射流不能充分發展的情形,如果仍采用射流理論分析,勢必帶來較大的誤差,使射流公式預測的結果可信度偏低。并且,射流理論分析方法只能給出室內的一些集總參數(即平均參數)性的信息,不能給出流場分布所需的詳細資料。隨著數值計算技術的發展,利用計算流體力學(CFD)技術對各種流場進行仿真是近年來普遍采用的一種新的方法,該方法在船舶工程領域也得到越來越多的應用。借助CFD數值模擬,設計人員可以對氣流流場進行形象化圖形演示,顯示出溫度場、壓力場、速度場等詳細的分布,可以形象直觀地為設計人員提供理論依據,幫助工程設計人員進行優化設計,提高工程設計質量,節省實驗所需的人力、物力和時間。針對典型艦船艙室大氣環境系統的優化,本文考慮用CFX軟件對典型艦船艙室大氣環境進行仿真,將數字仿真技術與艦船艙室大氣環境系統相結合,初步探索一種提高艙室大氣環境系統設計的方法。
2 典型艦船艙室大氣環境仿真及對比
2.1 數學模型
2.1.1模擬過程中的假設
1) 典型艦船艙室內氣流流動為紊態流動;
2) 艙室氣體是低速不可壓縮牛頓流體,作定常流動;
3) 忽略能量方程中由于粘性作用所引起的能量耗散;
4) 艙室內熱源均勻,表面溫度為定值。
2.1.2 RNGk-ε模型
本文仿真的典型艙室屬于高Re數的湍流流動,所以選擇RNGk-ε模型,它是由YAKHOT及ORZAG[1]提出的,該模型中的RNG是英文“Renormalization group”的縮寫,譯為“重正化群”。在RNGk-ε模型中,通過在大尺度運動和修正后的粘度項體現小尺度的影響,而使這些小尺度運動有系統地從控制方程中去除[2]。該仿真包含的控制方程如下:
連續性方程:
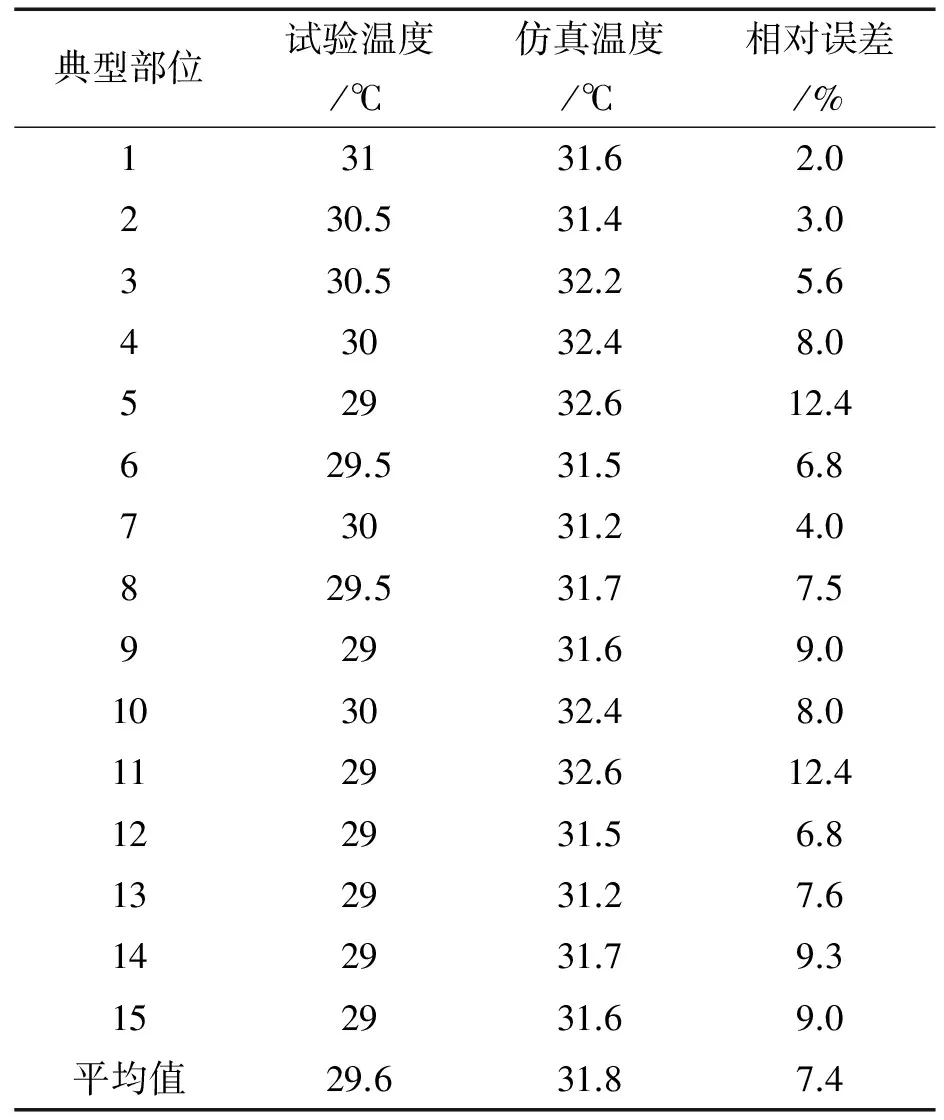
(1)
動量方程:
(2)
(3)
(4)
能量方程:
(5)
湍動能k方程:
+Gk-ρε
(6)
湍動耗散率ε方程:
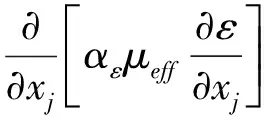
(7)
2.2 物理模型簡化
典型艦船艙室大氣環境仿真選擇的對象是動力機艙。下面是對模型進行簡化處理的介紹:
1) 壁面的肋骨、加強結構等不進行建模處理,并將艙壁處理成光滑的壁面結構。
2) 復雜的曲面船體采用近似的圓弧型壁面代替,減少建模的難度。
3) 對艙室內的小構件、小發熱體等不作建模處理,突出仿真建模的主要方面,忽略次要方面。
4) 動力機艙較大,且艙內設備布置基本對稱,為便于仿真建模及計算,只對動力機艙的一半(即右舷部分)進行建模仿真計算。
5) 艙內設備用近似的長方體或圓柱等來代替其外形輪廓,為利于網格的劃分,將代表大設備的長方體邊緣進行倒圓角處理。
6) 動力機艙的進/回風管路、進風口等也較多較復雜,為了仿真計算的準確性,將風管及風口也在模型中建立起來。
建模后的物理模型及進出風口如圖1所示。
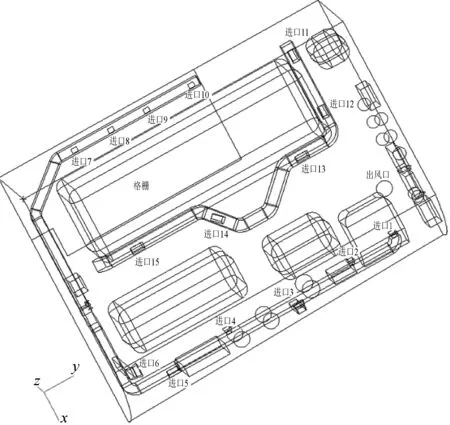
圖1 動力機艙物理模型及進出風口圖
2.3 進出口模型
2.3.1動量方法
1991年,陳清焰提出了用動量方法描述風口入流邊界條件[3]。動量方法用一個與原風口或散流器外形相同的矩形開口代替該風口或散流器,而將入口動量置為實際的空氣入口動量Jm,定義如下:
(8)
式中,vr為實際入流速度,L為實際入流風量,Ae為風口有效面積,A為風口外形總面積,f為風口有效面積和外形總面積之比,稱為有效面積系數,反映了風口或散流器有質量流入的面積(開口面積)占其外形總面積的比例,它可作為表征風口或散流器的面積出流特征的一個參數。藉此,動量方法可理解為“基本模型[4]”的極端:即用無數個“小的”矩形開口來代替實際的風口或散流器。
2.3.2仿真中絲網風口的處理
所建模型中的進、出風口由間距為10 mm×10 mm,直徑為1 mm的金屬絲網構成。進出風口絲網有效面積計算如圖2所示。
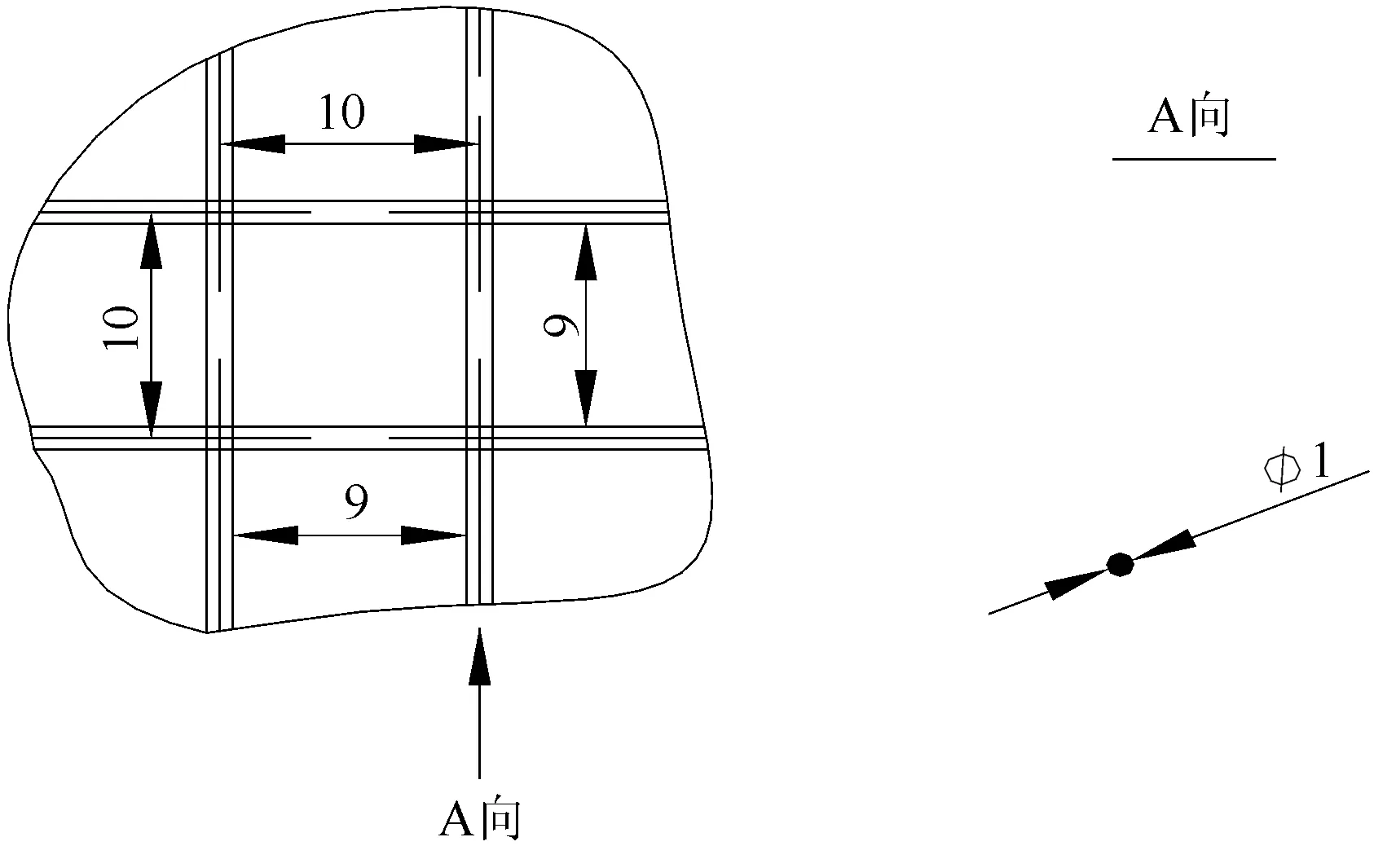
圖2 金屬絲網有效面積計算示意圖
有效面積系數f計算式:
(9)
按照風口的動量模型方法,各風口的風口面積、有效面積和風口速度見表1。
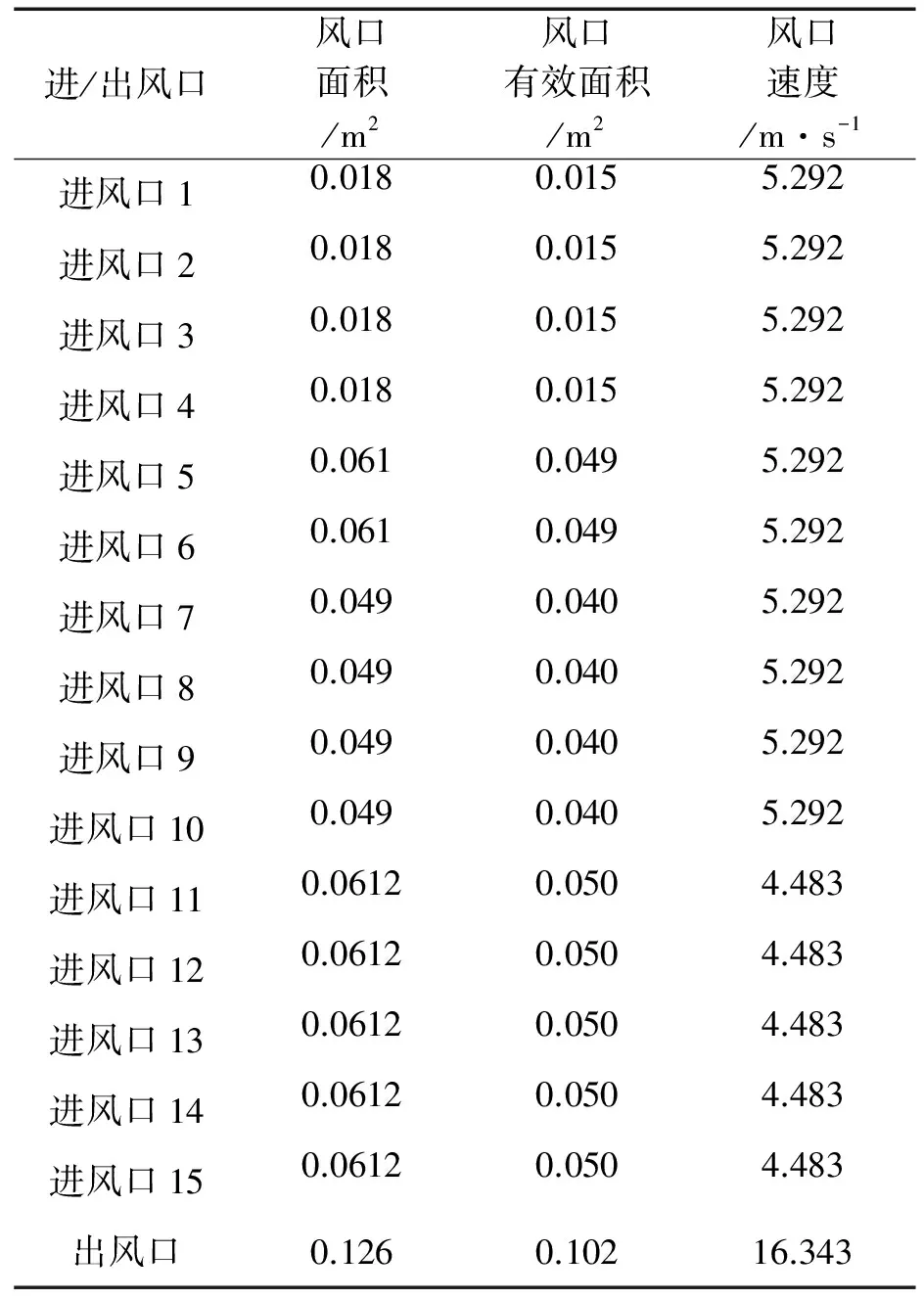
表1 各風口面積、有效面積及理論風速
2.4 物理邊界條件設置
2.4.1壁面函數
壁面函數法實際是一組半經驗公式,它將壁面上的物理量與湍流核心區內待求的未知量直接聯系起來,與高Re數k-ε模型配合使用能達到較理想的效果。
當y+<5時,所對應的區域是粘性底層,這時速度沿壁面法線方向呈線性分布,即:
u+=y+
(10)
當60 (11) 式中,κ為Karman常數;B和E是與表面粗糙度有關的常數,對于光滑壁面有κ=0.4,B=5.5,E=9.8。文獻[5]推薦將y+=11.63作為粘性底層與對數律層的分界點。 2.4.2進、出風口邊界 進風口邊界按表1所列的進風速度取值作為輸入邊界條件。 κ值按文獻[5]取來流進口的0.5%~1.5%計算,入口截面上的ε則可按下式計算: ε=Cμρk2/μt (12) 式中, 常數Cμ=0.09。 入口處μt按下式估算: ρuL/μt=100~1 000 (13) 出口處的邊界取為出口流量L=1.975 kg/s。 2.4.3固體壁面 仿真后的結果經過可視化處理,取Z=0.5 m處的平面溫度等值線、面圖如圖3所示。艦船試驗時,動力機艙典型部位測量點如圖4所示。 圖3 Z=0.5 m處平面溫度等值線、面分布圖 圖4 典型部位溫度測點位置示意圖 在正常工況下,外界環境溫度為31 ℃,濕度為83%時,動力機艙大氣環境系統運行1小時,艙室環境達到穩定后,試驗測點溫度值與仿真測點溫度值如表2所示。其中,試驗測點溫度值來自試驗記錄表,仿真測點溫度值來自圖3中相應典型部位的等值線、面的溫度值。 表2 試驗測點溫度與仿真測點溫度對比表 為便于分析比較,將表2轉化成圖5典型部位測點溫度對比圖的形式。 圖5 試驗測點溫度與仿真測點溫度對比圖 圖5中各測點處的仿真溫度值均大于試驗溫度值,原因在于:仿真中,艙內設備外表面均設為不工作時的初始環境溫度t=31 ℃,在仿真的過程中,該固定表面溫度成為熱源不斷地向艙室散發熱量,導致仿真測點處溫度普遍升高。從圖5溫度對比中可以看出,仿真的溫度場值大致反映了典型艙室大氣環境的運動趨勢,其中,大部分的溫度誤差在10%左右。由此推之,在對仿真對象進行細致的建模,并對其網格進行細化之后,仿真的結果可以達到工程實際應用所需的要求。 在仿真結果處理時,利用流線處理進風口1的出風路線時發現:靠近出風口處的進風口1出現了空氣短路現象。原因在于:出風口處的風量較大,出風速度很大,由伯努利原理可知該處壓力較低,進風口1距離出風口近,導致進風后直接流向出風口。該現象不利于能量的充分利用,并造成空氣組織不合理分布,在設計中應盡量避免。圖6顯示了進風口1的流向出風口的出風路線圖。 圖6 進風口1的短路現象 本文對典型艦船艙室大氣環境的溫度場進行了仿真,并提取了該艙室典型部位的仿真溫度場數據,將其與試驗數據進行了對比分析,分析結果表明:仿真的結果與試驗的結果之間的相對誤差≤12.4%,仿真結果和實驗結果比較吻合。同時,通過仿真的流線顯示了離出風口較近的風口送風短路的現象。因此,由以上結論可知,典型艦船艙室大氣環境仿真驗證了艙室大氣環境流動趨勢的正確性和參與工程實際設計的可行性,從而為設計和校驗艦船艙室大氣環境系統找到了一條可行的數值化途徑。 [1] YAKHOT V,ORZAG S A.Renormalization group analysis of turbulence:basic theory[J].J Scient Comput,1986,1:3-11. [2] 王福軍.計算流體動力學分析—CFD軟件原理與應用[M].北京:清華大學出版社,2004. [3] CHEN Q,MOSER A. Simulation of a multiple-nozzle difuser. Proceedings of the 12th AfVC Conference on Air Movement and Ventilation Control Within Buildings, Vol. 2[C].The IEAAir Infiltration and Ventilation Center, Ottawa, Canada, Semptember,1991. [4] 章梓雄,董曾南.粘性流體力學[M].北京:清華大學出版社,1998. [5] 陶文銓.數值傳熱學(第二版)[M].西安:西安交通大學出版社,2001.
3 結果對比分析與討論
3.1 仿真溫度圖數據處理
3.2 典型溫度對比
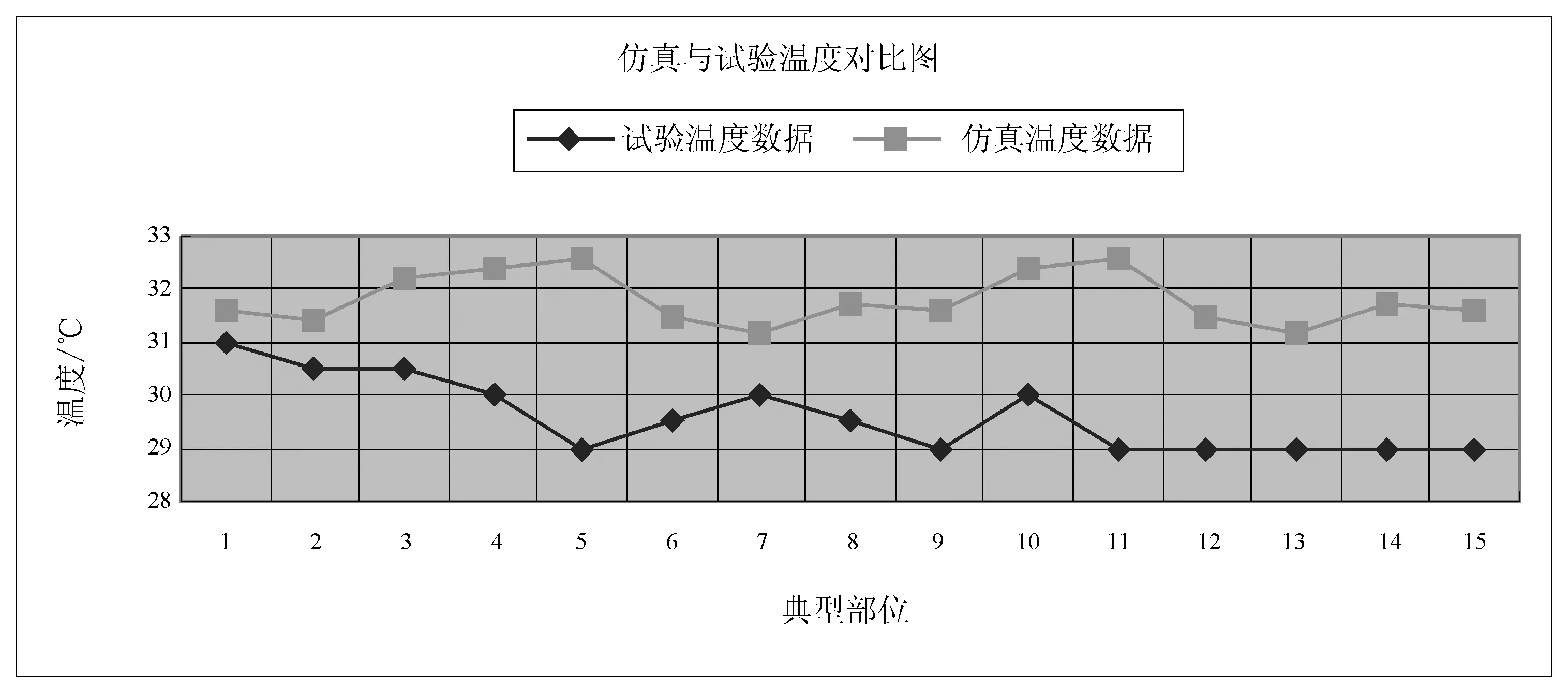
3.3 氣流短路現象分析
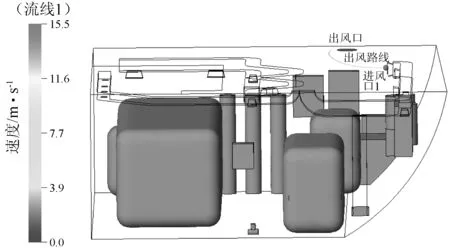
4 結 論

