改進遺傳算法在計算機數學建模中的應用

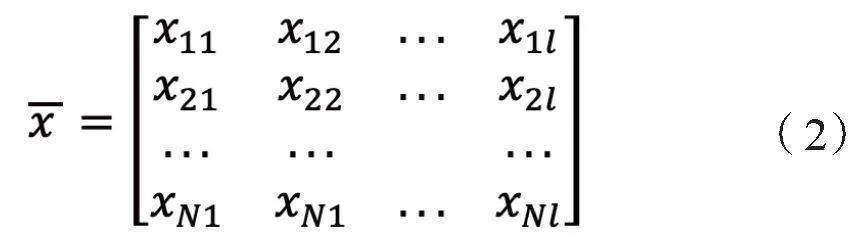
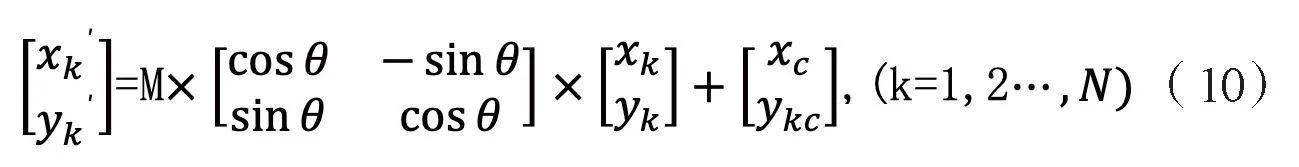
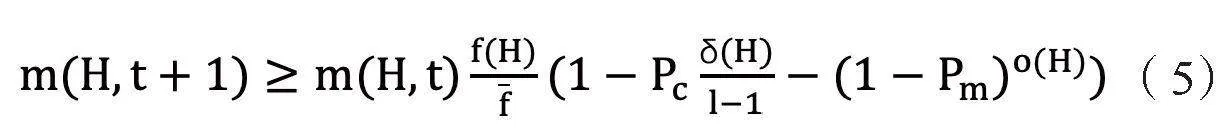
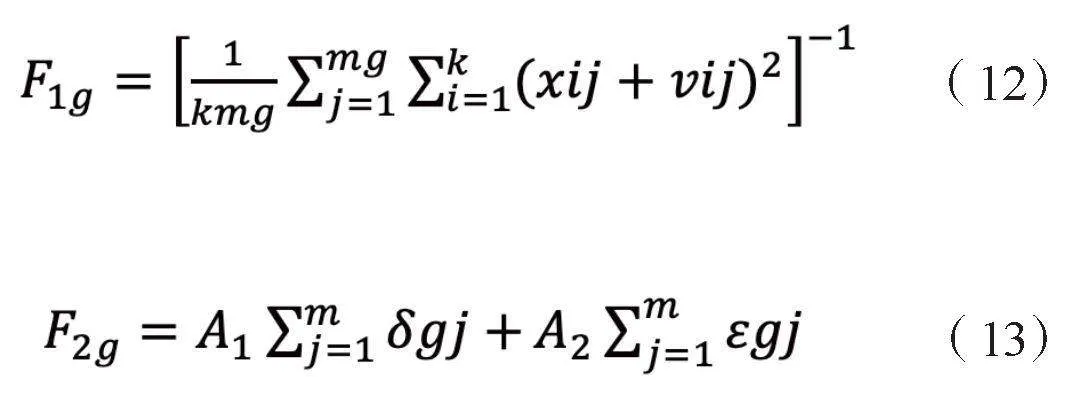
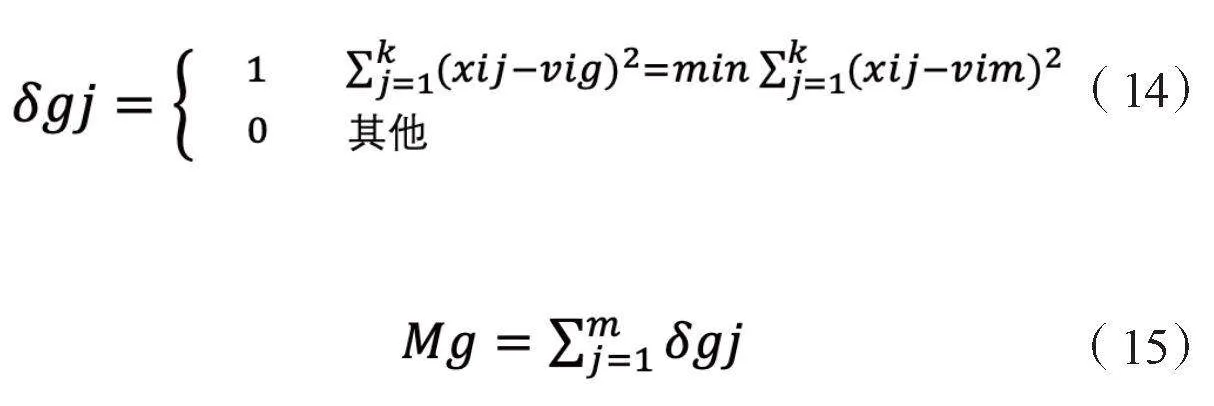
摘要：通過對遺傳算法的基本原理和流程進行分析，提出了一種基于多樣性維護和自適應機制的改進方案，并針對遺傳算法在計算機數學建模中的應用進行了改進與研究。方案在遺傳算法的選擇、交叉和變異操作中引入了多樣性維護策略，以增強算法的搜索能力和全局收斂性。實驗結果表明，所提出的改進算法在解決各種復雜數學建模問題時，具有更高的求解精度和收斂速度，驗證了其在實際應用中的有效性和優越性。

關鍵詞：改進遺傳算法；計算機；數學建模

一、前言

遺傳算法作為一種模擬自然界中生物進化的計算模型，已經在許多領域中得到了廣泛的應用，特別是在計算機數學建模中。遺傳算法通過模擬生物進化的過程，采用遺傳操作，如選擇、交叉和變異，來生成解決方案的種群，并通過適應度函數來評估和選擇優秀的解。為了改進遺傳算法在計算機數學建模中的應用，研究者們提出了一些改進策略。通過自適應調整交叉和變異率，以適應不同階段的搜索過程。對相關理論和實踐案例的分析，探討不同的改進策略，并評估它們在計算機數學建模中的效果，以提高遺傳算法在計算機數學建模中的應用性能和準確性。

二、標準遺傳算法與多種群遺傳算法

（一）基本算法簡介

1.遺傳算法

遺傳算法的思想是：首先將算法所研究的問題個體匯總，形成種群，然后用適應度函數計算各個體的自適應能力，將自適應能力較強的個體用交叉、變異算子等方式創造新的種群。

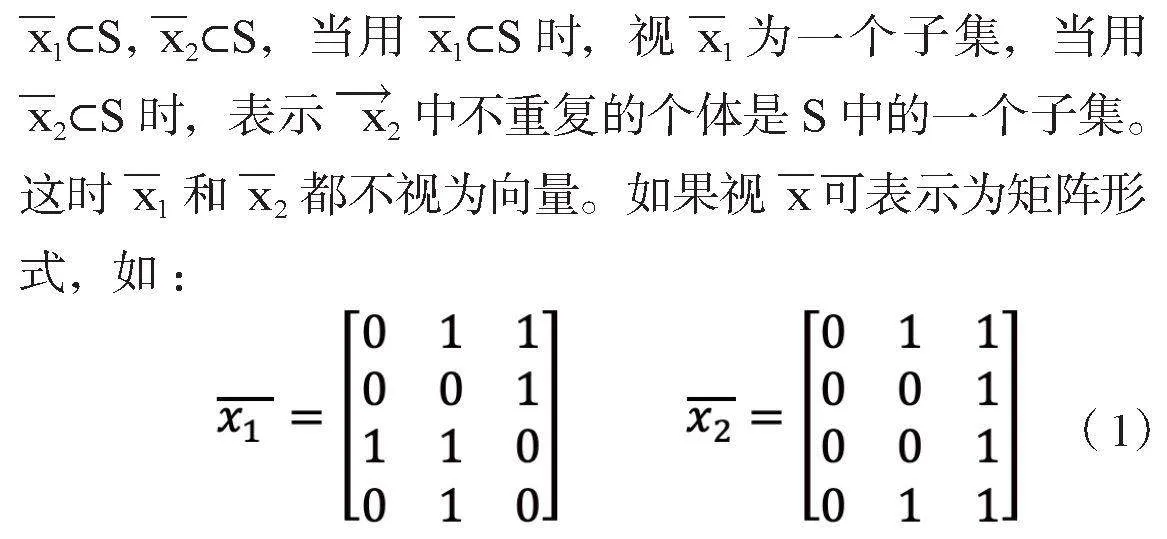
對于一個種群，由于是由個體構成的，因此它是個體空間的一部分，即是個體空間的一個子集。可以記為

對于鏈長為l種群規模為N的種群可以表示為N×l階矩陣。

選擇算子：選擇算子即是在一個種群中選擇一個個體，它是隨機映射：

特別地，按照概率規則 ：

遺傳算法通過反復進行選擇、交叉和變異操作，逐代優化種群中的個體，直到滿足停止條件為止。停止條件可以是達到最大迭代次數、適應度達到閾值或者種群收斂等[1]。

2.多種群遺傳算法

標準遺傳算法經常面臨多樣性問題，阻礙了它們的快速收斂，使算法結果陷入局部最優。多種群遺傳算法根據下度量方法來增加種群的多樣性：

（1）根據種群適應度標準差來增加種群多樣性。

（2）根據種群中熵值的不同變化增加種群多樣性。

（3）基于種群中各個個體不同的基因型來增加種群多樣性。

（二）傳統遺傳算法的優缺點

遺傳算法無需關注傳遞目標函數的微分值的過程，而是值通過函數值的適應度來判斷個體的表現。遺傳算法具有群體搜索的特點。它的研究過程從一個初始種群P（0）開始，這個種群有幾個個體，可以有效地避免尋找不需要的搜索點。使其研究過程更加簡便，參數對搜索結果的影響微乎其微。遺傳算法的包容性很強，可以和很多技術相結合解決問題[2]。

（三）多種群遺傳算法基本原理

多種群遺傳算法（Multi-Population Genetic Algorithm，MPGA）是遺傳算法的一種擴展，旨在通過同時演化多個種群來加速搜索過程，并提高全局搜索能力。將初始種群劃分為多個子種群，每個子種群獨立演化。通過實驗和分析調整多種群遺傳算法的參數，以優化算法性能[3]。模式定理從模式角度論證了N個初始種群在經過選擇、交叉、變異算子后模式H的變化：

其中，m（H，t+1）表示第t+1代種群H中模式所能匹配的樣本的數量，f（H）、f分別表示第t+1代所有模式H的平均適應度與種群平均適應度，l表示串的長度，Pc、Pm分別表示交叉概率與變異概率。

（四）多種群遺傳算法步驟流程

多種群遺傳算法（Multi-Population Genetic Algorithm， MPGA）是遺傳算法的一種變體，通過同時維護和演化多個種群來加速搜索過程，增加了種群間的交流和信息共享，從而提高了全局搜索能力。首先，初始化多個種群，每個種群包含一定數量的個體，這些個體是問題的潛在解的表示。可以采用隨機初始化或者基于啟發式方法的初始化來生成初始種群。對于每個種群中的個體，使用適應度函數評估其適應度，以確定其在解空間中的質量。通過實驗和分析，調整多種群遺傳算法的參數，以優化算法性能。

三、程序的實現

（一）仿真測試

1.測試的復雜二元函數介紹

函數1：

其中x的取值為（-3.0，12.1），y的取值為（4.1，5.8）。

函數2：

這兩個函數都屬于非線性函數，再給定的范圍之內分布著大量局部極大值，通常的搜索算法很容易在各自的局部極值中振蕩而無法跳出局部最優，比較適用于驗證多種群遺傳算法的優化性能。

2.測試的結果和分析

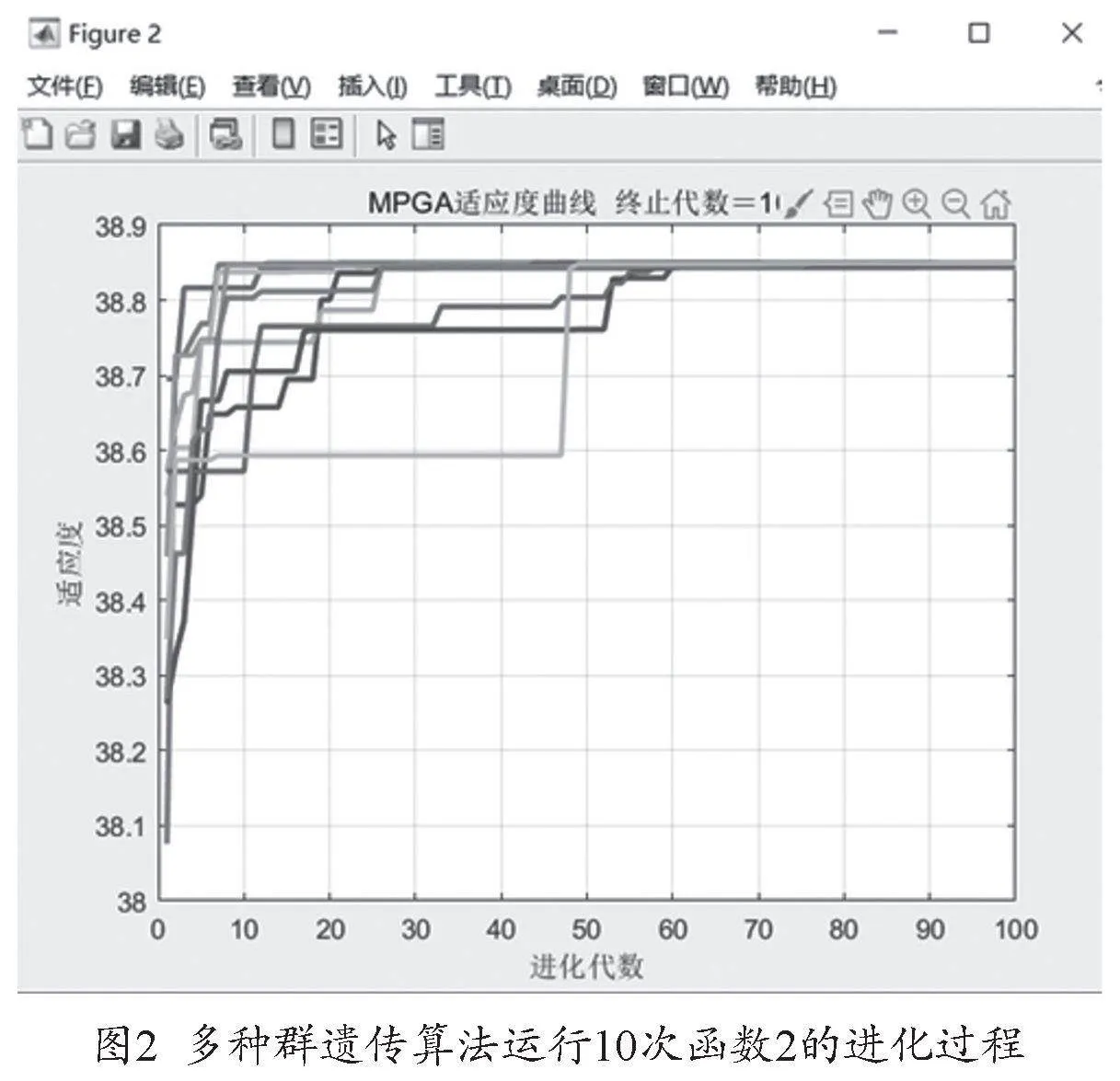
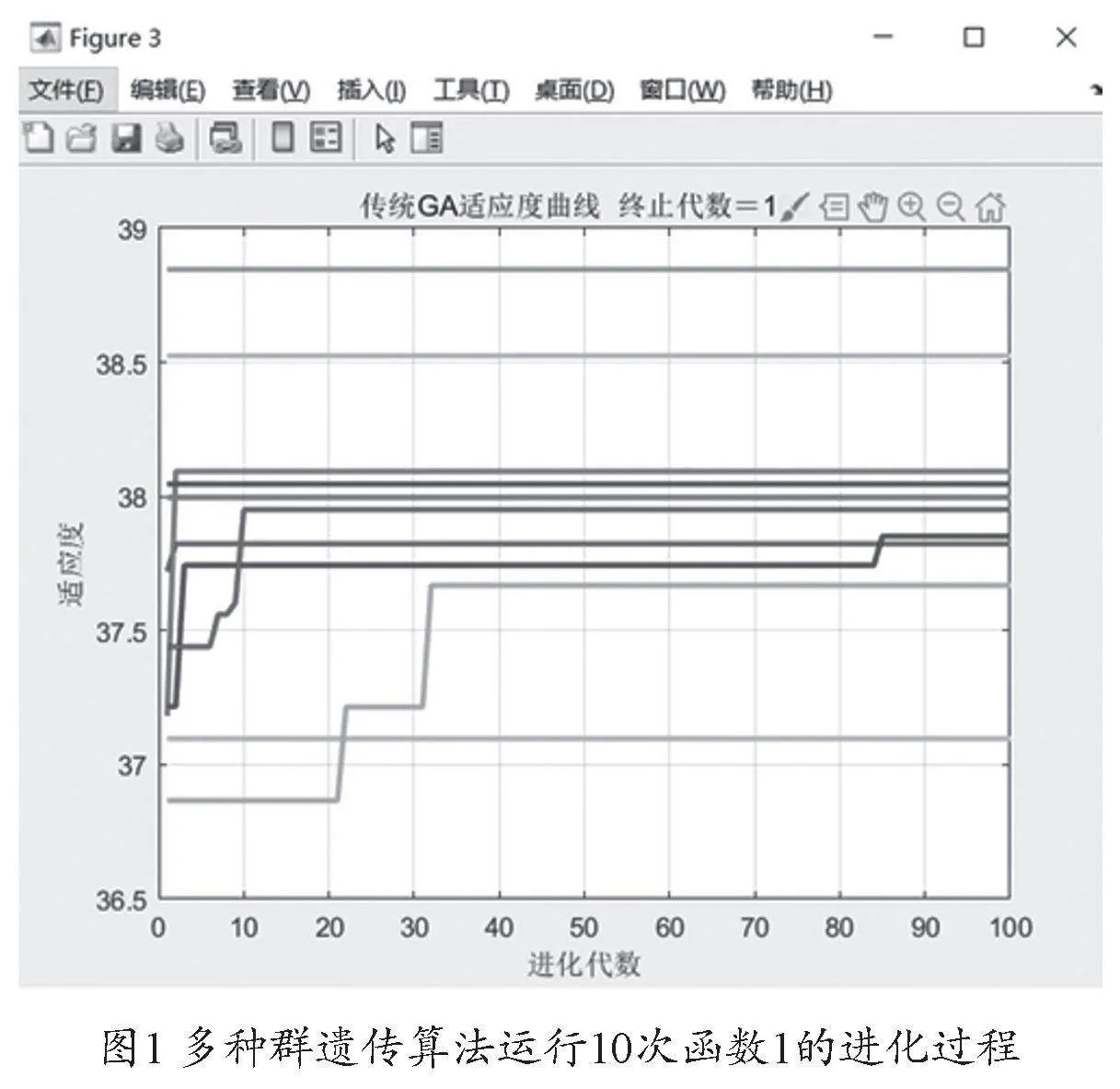
如圖1，10次得到的優化結果有很大差異，只有一到兩次的迭代，最終陷入局部最優，無法跳出，進化 100代得到的結果還是十分不穩定，函數的最終解還有很大的上升幅度，對于這種復雜的二元函數尋優，從結果表明傳統遺傳算法很難找尋最優解[4]。

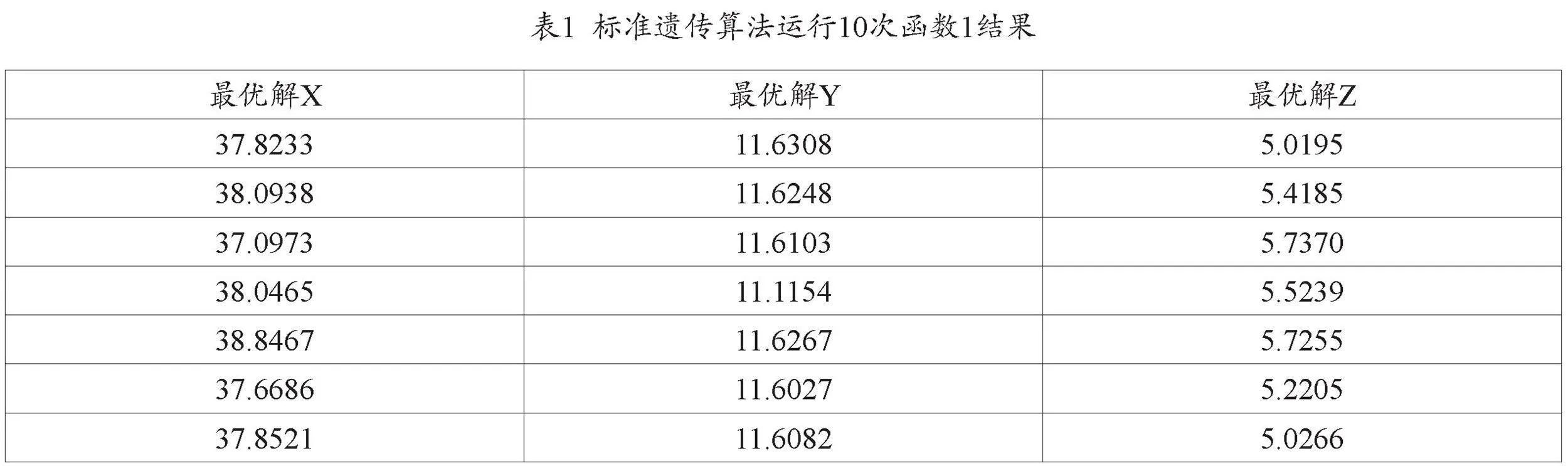
（二）數據分析

如表1，在使用多種群遺傳算法求得函數1通過近20次迭代，得到最優解是38.8503，對應的自變量：x=11.6255，y=5.7261，算法迅速跳出局部最優，得到最終結果。

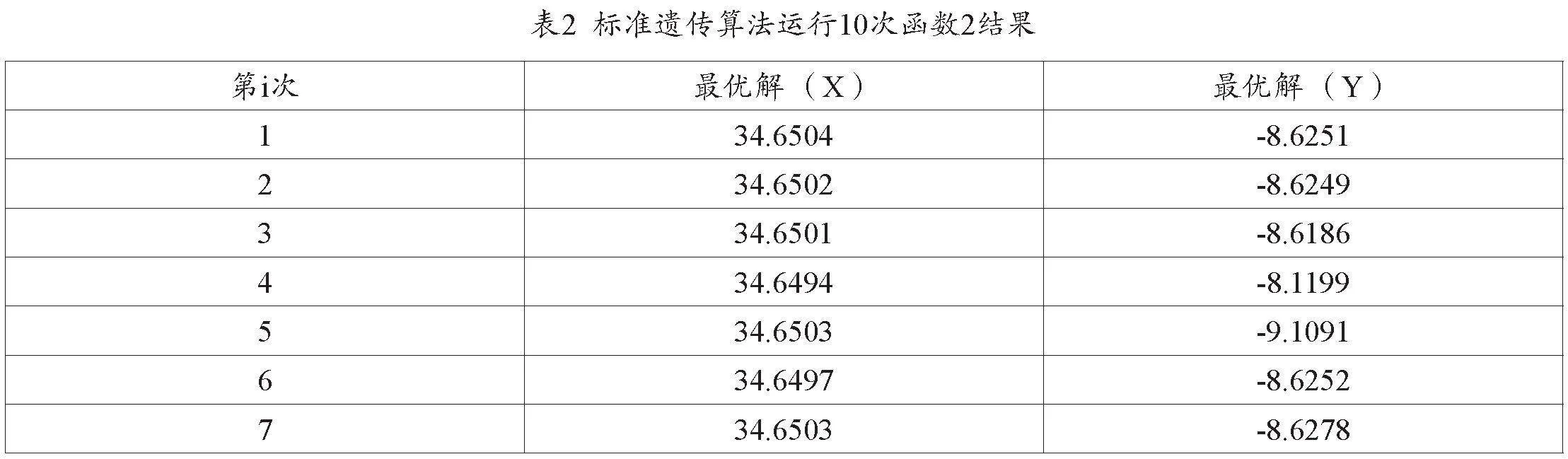
從表2中可以看出，使用標準遺傳算法運行函數2， 10次得到的最優解（X）和最優解（Y）存在一定的差異。其中，最優解（Y）的取值范圍在-8.6251到-8.1199之間。通過比較這10次運行的結果，可以觀察到算法在尋找最優解方面的穩定性。然而，這些最優解的具體數值和函數2的特性有關，需要進一步分析函數的圖像和特點才能給出更詳細的解釋。

四、改進遺傳算法在計算機數學建模中的應用

（一）無人機航跡規劃問題

無人機在飛行過程中需要避開障礙物，如建筑物、山脈、樹木等。改進的遺傳算法可以在航跡規劃中考慮避障問題，通過優化路徑來避免碰撞和危險情況的發生。在無人機航跡規劃中，通常存在多個沖突的目標，如最短路徑、最小能量消耗、最小風險等。改進的遺傳算法可以應用多目標優化技術，通過適當的權衡和調整，找到一組平衡的解來解決這些沖突目標。改進的遺傳算法可以應用于協同航跡規劃，通過優化多個無人機的航跡，實現協同飛行，提高任務效率和覆蓋范圍。

（二）圖像處理問題

待識別模式描述：

（x1，y1）為相對于模式原點的坐標，p1為相應的灰度值，將模式放大M倍，旋轉θ，并將模式原點平移至（x2，y2），點列變為p'：

其中

對于二值圖像（背景色為白色，前景色為黑色）而言，我們可以定義待識別模式與圖形庫中相似圖形的匹配率R作為識別性能的評價指標，0≤R≤1。

式中Nb為點序列p'中滿足p（xk'，yk'）=p（xk，yk）（k=1，2，…，N）的p=（xk'，yk'）=p（xk，yk）（k=1，2…，N）點個數。

在區分復雜的圖像方面，信息的流動經常被適當的分割，因此需要很大程度解決優化問題。多種群遺傳算法的應用不僅可以迅速選擇出最優化的方案，而且大大縮短了計算所消耗的時間。并使用適應性基因參數在兩個層次上進行培訓大大提高了圖像處理的時效性和準確性。

（三）數據挖掘問題

由于一個N×N的數字圖像可以分成若干個n×n的圖像塊，每一個塊成為一個K維矢量K=n×n，這樣一個圖像可以分成（Ⅳ／n），Vg（vig）那么目標函數可表示成：

在一系列侯選電報密碼中，Vc（Vi，i=l，2…，m）Vg代碼字為：

第二階段可以改進VQ碼中的馬塞克結果。

Xj（xij）∈Rg，Vg（vig）∈Vc，Rg中i行j列圖像塊和i維Vg代碼的差小于ε時，Nij=1，δgj是那些圖像塊總數和電報密碼Vg。改進個體的編碼方案，使其更符合問題的結構特征，從而減少搜索空間。優化選擇策略，使得適應度高的個體更有可能被選擇，并保留多樣性以防止早熟。常見的選擇策略包括輪盤賭選擇、錦標賽選擇、精英保留等。引入自適應機制來動態調整遺傳算法的參數，以適應不同問題和不同階段的搜索需求[5]。

五、結論

本文針對遺傳算法在計算機數學建模中的應用進行了研究，改進了遺傳算法，并通過實例驗證了改進算法的有效性和優越性。改進算法在解決計算機數學建模問題時，能夠更好地保持種群的多樣性，提高全局搜索能力，避免早熟收斂，從而提高求解質量和效率。通過對改進遺傳算法的深入研究，本文提出了相應的參數設置策略和求解方法，為遺傳算法在計算機數學建模領域的應用提供了有益的理論和實踐指導。

參考文獻

[1]孫慶鋒，方來祥，戴柯寒.改進遺傳算法及最小二乘法在計算機數學建模中的應用[J].電子技術與軟件工程，2016（03）：175.

[2]秦文科.改進遺傳算法在結構損傷診斷中的應用研究[J].工程技術研究，2022，7（14）：13-15.

[3]劉曄.計算機軟件在數學建模中的應用優勢與實踐研究[J].信息系統工程，2023（09）：71-74.

[4]郭曉玲.計算機技術在數學建模領域的應用研究[J].信息記錄材料，2019，20（10）：130-131.

[5]楊博，劉樹東，魯維佳，等.改進遺傳算法在機器人路徑規劃中的應用[J].現代制造工程，2022（06）：9-16.