基于二次指數平滑和多元線性回歸的寧波市港口物流需求預測分析

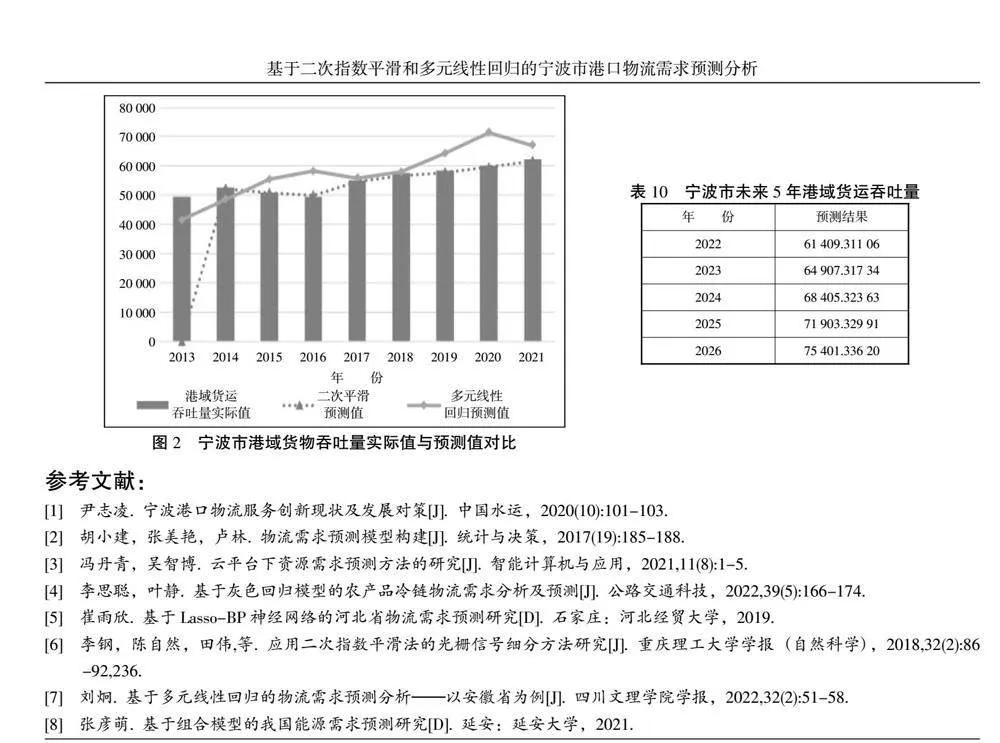
摘" 要：隨著經濟全球化的發展，港口作為物流發展的重要環節，港口物流需求已經成為港口資源配置規劃和進出口貿易的重要依據。為對寧波市港口物流需求進行科學合理的預測，文章借助SPSS等數據分析軟件，使用二次指數平滑和多元線性回歸分別對其物流需求進行預測，通過對比兩種預測方法的精度，最后發現，二次指數平滑法的預測精確度要優于多元線性回歸法，并通過二次指數平滑法預測寧波市未來五年的港口物流需求量。

關鍵詞：二次指數平滑；多元線性回歸；港口物流需求預測

中圖分類號：F550" " 文獻標志碼：A" " DOI：10.13714/j.cnki.1002-3100.2024.17.020

Abstract： With the development of economic globalization， as an important part of logistics development， port logistics demand has become an important basis for port resource allocation planning and import and export trade. In order to make a scientific and reasonable forecast of Ningbo Port logistics demand. With the help of data analysis software such as SPSS， this paper uses quadratic exponential smoothing and multiple linear regression to forecast its logistics demand respectively. By comparing the accuracy of the two forecasting methods， it is finally found that the forecasting accuracy of quadratic exponential smoothing is better than that of multiple linear regression， and the port logistics demand of Ningbo in the next five years is predicted by quadratic exponential smoothing.

Key words： second exponential smoothing method; multiple linear regression; port logistics demand forecast

0" 引" 言

港口是國際貿易物流鏈中的重要節點，發揮著綜合交通運輸樞紐的角色，是國家經濟社會發展的重要戰略資源和支撐[1]。寧波作為世界型港口城市，物流業一直在經濟發展中占據重要地位。作為“第三方利潤源”，隨著經濟發展的深入，市場競爭方式逐漸從單一的價格戰轉變為技術、服務、管理的多元化競爭。根據《寧波市國民經濟和社會發展第十四個五年規劃和二O三五年遠景目標綱要》可知，寧波充分利用其所擁有的地理優勢，積極構建以港口物流為主的現代物流產業體系，目前已基本完成“十三五”物流發展規劃目標任務，繼續為實現“十四五”時期物流高質量發展而努力。因此，物流業對寧波的經濟發展有重要影響，對寧波市進行物流需求預測可以有助于該市合理運用有效資源和制定相關經濟政策。……