巧用圓的參數方程求最值

【摘要】與圓有關的最值問題是近年來高考數學（非解答題）的熱點之一.用參數方程解答相關題目往往較用別的方法更便捷，比如利用圓的參數方程x=a+rcosθy=b+rsinθ（θ為參數）可以簡化探究距離、長度、定值或取值范圍等問題的運算，大大提高解題效率.本文通過析題對比不同解法加以說明.

【關鍵詞】高中數學；圓；參數方程

1巧解數量積的取值范圍問題

1.1題目呈現

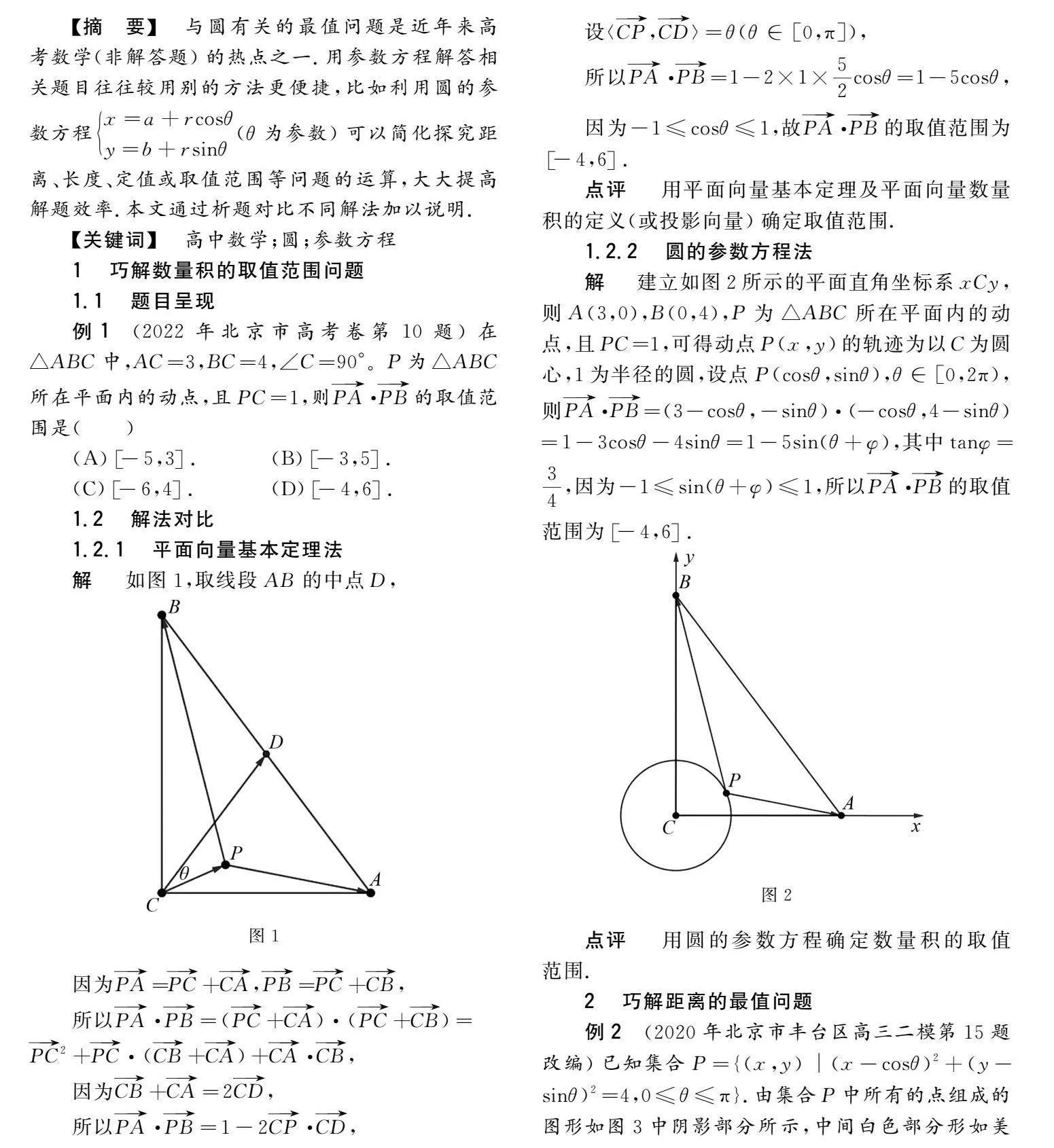
例1（2022年北京市高考卷第10題）在△ABC中，AC=3，BC=4，∠C=90°。P為△ABC所在平面內的動點，且PC=1，則PA·PB的取值范圍是（）

（A）－5，3.（B）－3，5.

（C）－6，4.（D）－4，6.

1.2解法對比

1.2.1平面向量基本定理法

解如圖1，取線段AB的中點D，

因為PA=PC+CA，PB=PC+CB，

所以PA·PB=（PC+CA）·（PC+CB）=PC2+PC·（CB+CA）+CA·CB，

因為CB+CA=2CD，

所以PA·PB=1－2CP·CD，

設〈CP，CD〉=θ（θ∈［0，π］），

所以PA·PB=1－2×1×52cosθ=1－5cosθ，

因為－1≤cosθ≤1，故PA·PB的取值范圍為－4，6.

點評用平面向量基本定理及平面向量數量積的定義（或投影向量）確定取值范圍.

1.2.2圓的參數方程法

解建立如圖2所示的平面直角坐標系xCy，則A（3，0），B（0，4），P為△ABC所在平面內的動點，且PC=1，可得動點P（x，y）的軌跡為以C為圓心，1為半徑的圓，設點P（cosθ，sinθ），θ∈［0，2π），則PA·PB=（3－cosθ，－sinθ）·（－cosθ，4－sinθ）=1－3cosθ－4sinθ=1－5sin（θ+φ），其中tanφ=34，因為－1≤sin（θ+φ）≤1，所以PA·PB的取值范圍為－4，6.

點評用圓的參數方程確定數量積的取值范圍.

2巧解距離的最值問題

例2（2020年北京市豐臺區高三二模第15題改編）已知集合P={（x，y）∣（x－cosθ）2+（y－sinθ）2=4，0≤θ≤π}.由集合P中所有的點組成的圖形如圖3中陰影部分所示，中間白色部分形如美麗的“水滴”. 則在集合P中任取一點M，則M到原點的距離的最大值為.

解設點M（cosθ+2cosα，sinθ+2sinα），α∈［0，2π），

則MO=|MO|

=（cosθ+2cosα）2+（sinθ+2sinα）2

=5+4cos（θ－α），

因為－1≤cos（θ－α）≤1，所以M到原點的距離的最大值為3.

例3（2019年清華大學領軍計劃第3題）已知P為單位圓上一動點，且A（0，2），B（0，－1），求|AP||BP|2的最大值.

解設點P（cosθ，sinθ），θ∈［0，2π），

則|AP|=|AP|=5－4sinθ，

|BP|2=BP2=2+2sinθ，

所以|AP||BP|2=5－4sinθ（2+2sinθ）=（5－4sinθ）（2+2sinθ）2，

當θ≠3π2時，則5－4sinθ>0，2+2sinθ>0，

所以，|AP||BP|2≥

（5－4sinθ）+（2+2sinθ）+（2+2sinθ）33

=33，

當5－4sinθ=2+2sinθ，即sinθ=12時取等號；

當θ=3π2時，則P（0，－1），所以|AP||BP|2=0，

綜上，|AP||BP|2的最大值為33.

3巧求參數的取值范圍問題

例4過點A（m，2）作直線l與圓C：x2+y2=1交于M，N兩點，若M點恰好是線段AN的中點，則實數m的取值范圍是.

解設M（cosθ，sinθ），θ∈［0，2π），則N（2cosθ－m，2sinθ－2），代入圓方程得，4cos2θ－4mcosθ+m2+4sin2θ－8sinθ+4=1，化簡得4mcosθ+8sinθ=m2+7，在θ∈［0，2π）上有解，因為4mcosθ+8sinθ=16m2+64sin（θ+φ），其中，tanφ=m2，所以m2+7≤16m2+64，解得m∈［－5，5］.

例5已知圓的方程為x2+y2=1，點P（x，y）是圓上的任一點，則不等式x+y+xy≥t2+2t－4恒成立，則實數t的取值范圍為.

解設P（cosθ，sinθ），θ∈［0，2π），則x+y+xy=cosθ+sinθ+cosθsinθ，

因為cosθsinθ=（cosθ+sinθ）2－12，

所以，x+y+xy=cosθ+sinθ+（cosθ+sinθ）2－12=12（cosθ+sinθ+1）2－1，

因為cosθ+sinθ=2sin（θ+π4）∈［－2，2］，

所以，x+y+xy∈［－1，1+222］，因為不等式x+y+xy≥t2+2t－4恒成立，

所以，－1≥t2+2t－4，即t2+2t－3≤0，所以實數t的取值范圍為［－3，1］.

4結語

例1中的兩種方法將與圓相關的最值問題，轉化為由輔助角公式得到的三角函數值域問題，通過代數運算輕松解決了復雜的幾何問題.例3中，同樣的是利用三角函數及基本不等式將兩條變化的距離問題進行了代數坐標化，從而實現了通過代數運算降低幾何抽象帶來的思維困難.例4及例5通過參數方程得到的三角函數的有界性，由此確定函數最值，解得不等式得到參數的范圍.因此，我們不難發現利用圓的參數方程解決最值問題，實質上就是用三角代換表示圓上的動點坐標，通過將幾何問題代數坐標化，轉化為三角函數的值域問題，這種處理問題的方式明顯達到了事半功倍的效果.

參考文獻：

[1]張樹鵬.破解向量最值問題的三種有效途徑[J].數學學習與研究，2017（11）：126.

[2]蔣偉.化繁為簡巧用圓的參數方程解題[J].理科考試研究，2015，22（03）：7.