基于貝葉斯優化隨機森林輸電線路故障識別方法

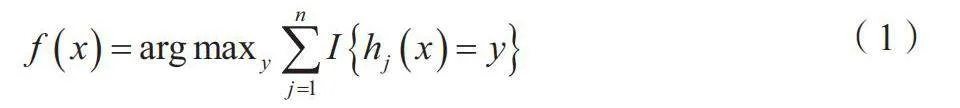
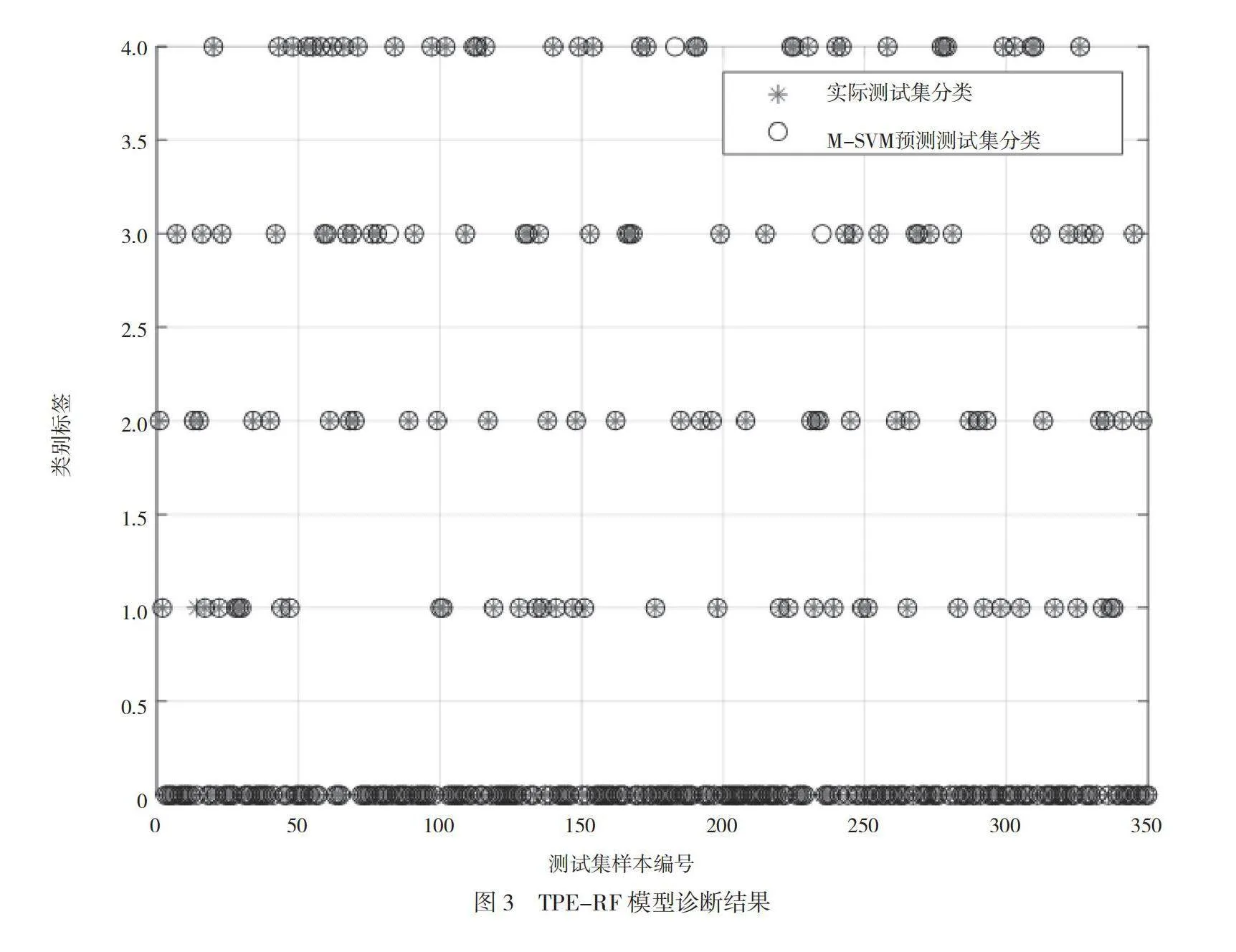
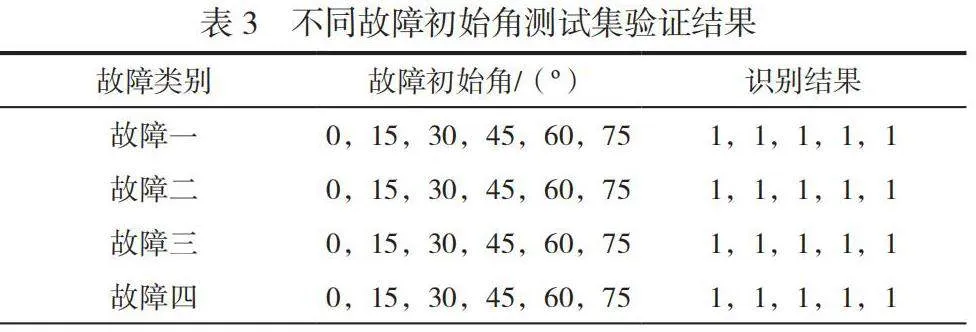
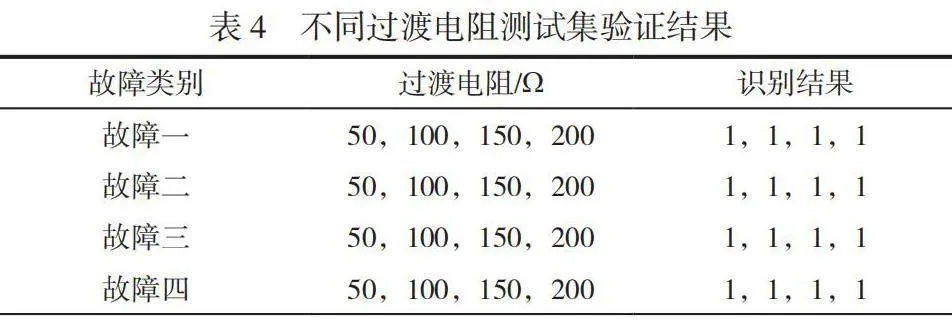
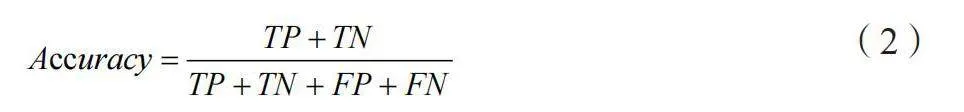
摘 要：針對輸電線路線路故障精度低的問題，本文提出一種貝葉斯優化隨機森林（Random Forest，RF）的輸電線路故障識別方法。通過經驗模態分解提取故障特征，構成特征集，采用貝葉斯優化RF來挖掘特征集與短路故障類型之間的關系。結果表明，TPE-RF能快速優化超參數，提高診斷精度，避免過渡電阻、故障初始角的影響。

關鍵詞：輸電線路；故障識別；經驗模態分解；貝葉斯優化；RF算法

中圖分類號：TM 75" " " " " " " 文獻標志碼：A

高壓輸電線路發生短路故障會對經濟、工業生產和消費用電等造成重大影響。因此，快速、準確地辨識短路故障類型和發生故障的位置能夠加快故障線路檢修速度，減少故障帶來的經濟損失[1-2]。

本文提出了一種基于貝葉斯優化隨機森林的輸電線路故障識別方法（Tree-structured Parzen Estimator-Random Forest，

TPE-RF）。通過經驗模態分解（Empirical Mode Decomposition，EMD）提取數據，得到固有模態函數（Intrinsic Mode Function， IMF），提取樣本熵，構成特征集。結合改進的RF算法訓練并測試特征樣本集，識別輸電線路短路故障具體類型。仿真結果表明，該方法可以高效識別輸電線路的短路故障類型。

1 特征提取

1.1 EMD

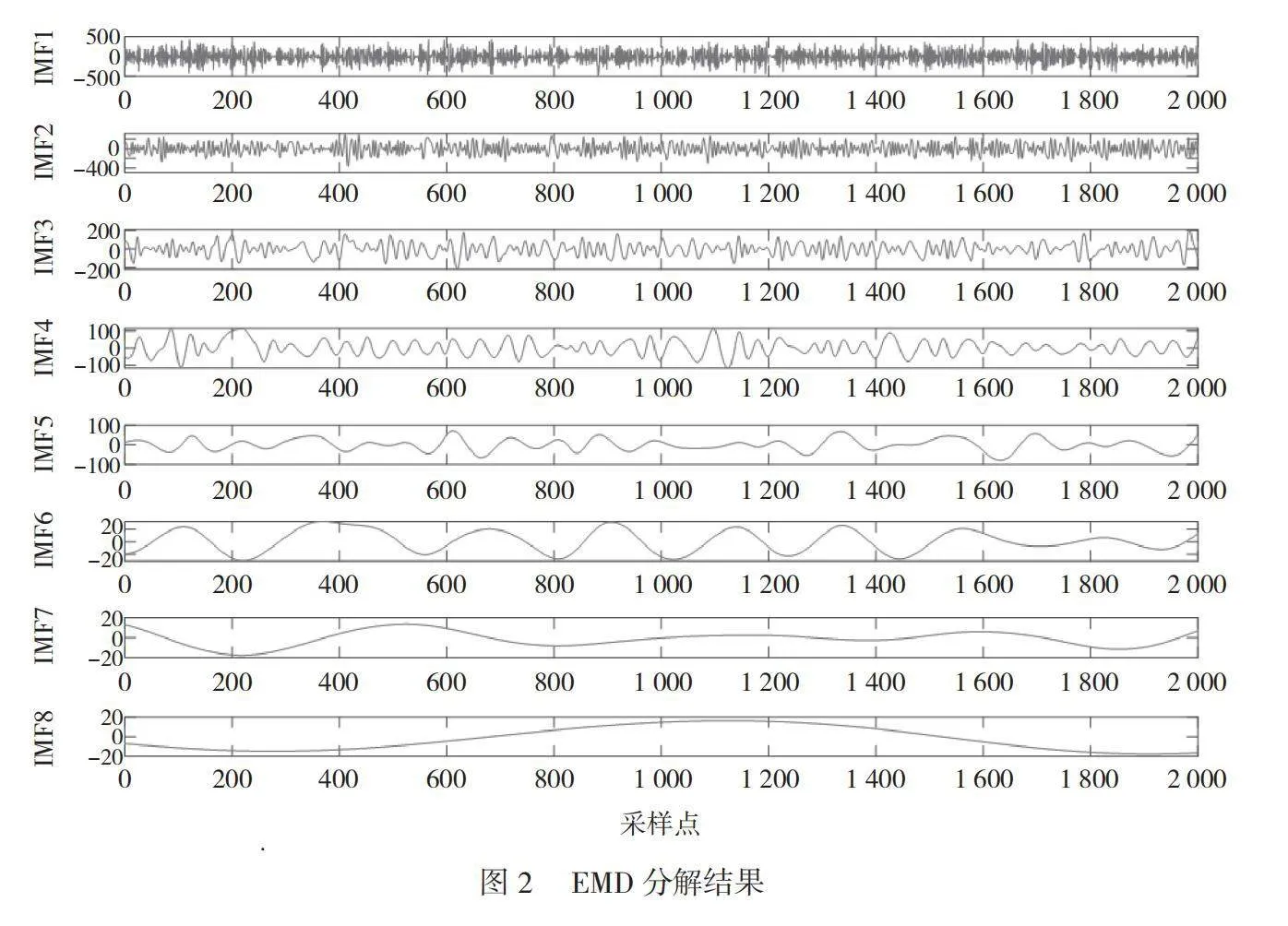
EMD是一種自適應的信號處理方法，特別適合處理非平穩和非線性的信號數據。通過EMD，可以將復雜的信號分解為1組IMF分量[3]。這些IMF分量能說明信號的內在結構和動態特性，并分析非線性、非穩定的信號。當處理復雜信號時，這種分解方法優勢突出，效果明顯，因此在許多領域都應用廣泛。

1.2 樣本熵

樣本熵是一種度量信號復雜性的工具，能夠說明信號序列的結構[4]。使用樣本熵能夠更精確、高效地提取故障信號的特征信息，為后續的診斷和分析提供有力支持。

2 貝葉斯優化的隨機森林模型

機器學習能夠充分挖掘非線性、混疊嚴重的故障信號的敏感特征，并剔除虛假特征，因此在國內外輸電線路故障診斷領域逐漸成為研究熱點。

2.1 隨機森林

隨機森林是一種基于決策樹的集成學習算法，通過構建多個決策樹并綜合它們的分類結果來分類[5]。與單一決策樹相比，隨機森林具有分類精度更高、穩定性更好和抗噪聲能力更強等優點。在訓練過程中，隨機森林中的每個決策樹都是獨立構建的，以增加模型的多樣性，降低過擬合風險。綜合多個決策樹的分類結果，利用隨機森林進一步提高分類精度。隨機森林還保留了多值分類的特性，因此特別適合解決多值分類問題。在隨機森林中的每個決策樹不是利用弱學習器來逐步提高模型的性能的，而是獨立構建的，因此，與其他方法（例如 Boosting）相比，當面對數據噪聲時，隨機森林的穩定性更好，其可以通過引入隨機性來避免過擬合問題，并提高模型的泛化能力。綜上所述，隨機森林是一種強大而有效的分類器，適合處理多值分類問題。

設原始訓練集X={（x1，y1），（x2，y2），（xN，yN）}，xm=[xm1，xm2，xmn]為第m個訓練樣本，n為xm中特征值個數，xm為訓練樣本，ym為類別標簽。利用Bootstrap方法從原始訓練樣本集Xj（j=1，2，…n，）中隨機抽取多個訓練樣本子集，構建決策樹模型hj（x），獲得1組決策樹組成的分類器{h1（x），h2（x），h3（x），hj（x）}（j=1，2，…n）。當測試樣本輸入訓練好后的分類器時，這組決策樹對樣本類別進行投票，以確定其最終分類。通過這種方式，隨機森林整合多個決策樹的優勢，提高了分類的準確性和穩定性。其分類決策如公式（1）所示。

（1）

式中：hj（x）為第j棵決策樹；I{·}為示性函數，當括號中的表達式滿足條件時，其值為1，否則為0；y為樣本的類別標簽；f（x）為第j棵決策樹的分類結果；n為決策輸個數。

2.2 貝葉斯優化的隨機森林

在機器學習過程中，由于模型參數直接影響訓練效果，因此參數設置十分重要，須在訓練前設置RF的參數，例如樹的最大深度、每個決策樹的最大葉子數量和學習率等。如果參數復雜，就會導致其可能的組合更多，人工調參更費時、費力且不一定能夠挖掘合適的組合，貝葉斯算法調參迭代次數少，速度快，能快速找到模型最佳參數組合。為了提高模型性能，本文采用貝葉斯算法。貝葉斯[6]算法流程執行步驟如下。步驟一：設置待優化參數范圍并初始化。為了保證算法穩健、準確，需要對RF的各參數設定一個合理的取值范圍。步驟二：估計概率密度，計算增益期望（Excepted Improvement，EI）。確定參數范圍后，估計概率密度。該步驟

的核心是通過采集函數來計算EI，EI反映參數組合的性能。步驟三：利用最佳參數組合訓練預測模型。將EI值最大的參數組合輸入RF預測模型中進行訓練。步驟四：精度驗證與算法迭代。步驟五：評估預測結果的精度是否滿足預期。如果滿足，算法就可以終止；如果不滿足，就需要返回步驟二重新開始，直至找到滿足精度要求的最佳參數組合為止。

2.3 評價指標

為了準確評估模型的分類性能，本文采用準確率（Accuracy）作為評價指標，計算過程如公式（2）所示。

（2）

式中：TP（真正）為將正類樣本預測為正類的數量；TN（真負）為將負類樣本預測為負類的數量；FP（假正）為將負類樣本預測為正類的數量；FN（假負）為將正類樣本預測為負類的數量。

公式（2）結果越接近1，模型的準確度越高。

2.4 短路故障類型識別算法流程

TPE-RF故障類型識別方法包括以下4個執行步驟。步驟一：收集原始數據，為了方便計算，符合數據輸入的要求，預先對數據進行歸一化處理。步驟二：通過經驗模態分解，提取已歸一化數據，計算樣本熵，構成特征集，并按照一定比例分成訓練集與測試集。步驟三：將訓練集數據作為輸入，訓練TPE-RF模型，使其能夠學習并識別數據中的模式和特征。步驟四：將測試集數據輸入已經訓練好的TPE-RF模型中，得到模型的識別結果。這個結果可以用于評估模型的性能和準確度，進一步優化模型參數或結構。

3 仿真分析

3.1 輸電線路案例

基于Simulink環境搭建輸電線路仿真模型，輸電線路結構如圖1所示。正序參數：電阻為1.648×10-2 Ω/km，電抗為1.348 mH/km，電容為8.68×10-3 μF/km。零序參數：電阻為0.3 Ω/km，電感為3.639 mH/km，電容為6.166×10-3 μF/km。

本文從輸電線路仿真中選取過渡電阻、故障位置、故障類型和故障角度進行故障仿真。故障參數設置見表1。

短路故障類型為單相接地短路故障、相間短路故障、兩相接地短路故障和三相接地短路故障，用標簽識別不同類別的短路故障，類別標簽見表2。

3.2 特征提取

在電力系統中，當線路發生故障導致跳閘時，會產生一系列電弧和各次諧波。本文采用EMD方法，深入分析線路兩端的電流波形。EMD能夠將復雜的電流波形分解為多個IMF分量，這有助于更細致地研究電流波形的特點，準確識別故障。在仿真試驗部分，利用Simulink模型模擬瞬時性故障和永久性故障。為了保證研究的準確性，選取從故障發生至合閘前的故障相電流作為分析的電流信號。在MATLAB軟件中，利用EMD分解這些信號，得到多個IMF分量。

以故障相角差為15°的金屬性接地故障為例，當故障點位于距離首段50%的位置時，利用EMD深入分解瞬時性故障和永久性故障的電流信號，結果如圖2所示。前7個IMF分量已經包括原始數據的大部分信息。因此，以這7個IMF分量作為原始信號的代表，計算樣本熵，構建特征集。采用該方法不僅提高了故障識別的準確性，還為電力系統中的故障診斷提供一種有效的分析手段。

3.3 故障類型識別結果

本文提出TPE-RF模型，診斷結果如圖3所示。橫軸為測試樣本編號，縱軸為故障對應編號，模型準確率高達98.85%。

3.4 TPE-RF模型驗證分析

為了驗證TPE-RF故障識別模型的穩定性，本節驗證了4種類型的短路故障在不同過渡電阻和不同故障初始角狀態中的情況，驗證結果見表3。

3.4.1 不同故障初始角驗證分析

從表3可以看出，TPE-RF模型在各故障相角范圍內均能準確識別短路故障類型，這說明TPE-RF模型的魯棒性較強，能夠適應不同的故障相角條件并識別故障類型。這個結果表明，當處理輸電線路故障時，TPE-RF模型能夠有效地克服故障相角的影響。

3.4.2 不同過渡電阻驗證分析

不同過渡電阻測試集驗證結果見表4，從表4可以看出，TPE-RF模型在各過渡電阻范圍內均能準確準確識別短路故障類型。這表明TPE-RF模型具有較強的魯棒性，能夠適應不同的過渡電阻條件并識別故障類型。這個結果表明，TPE-RF模型在處理輸電線路故障的過程中，能夠最大程度地減少過渡電阻的影響。

4 結論

本文提出了一種基于TPE-RF的輸電線路故障識別方法。該方法準確率更高，達到98.85%。研究表明，基于TPE-RF的輸電線路故障識別模型對短路故障識別中的過渡電阻、初始故障角都有顯著影響，它適應性良好，能夠準確識別輸電線路短路故障的類型。

參考文獻

[1]宋國兵，陳哲鴻，侯俊杰，等.基于電荷量變化特征的高壓直流線路縱聯保護[J].電力系統及其自動化學報，2020，32（10）：9-16.

[2]費春國，霍洪雙.基于電流振幅與SVM的輸電線路故障分類[J].電力系統及其自動化學報，2019，31（4）：139-144.

[3]王仲平，何黎黎，丁更乾.基于EMD-LSTM-ARMA模型短期發電量組合預測[J].現代電子技術，2023，46（3）：151-155.

[4]蘇文勝，王奉濤，朱泓，等.基于小波包樣本熵的滾動軸承故障特征提取[J].振動測試與診斷，2011，31（2）：5.

[5]楊杰，吳浩，董星星，等.基于電流故障分量特征和隨機森林的輸電線路故障類型識別[J].電力系統保護與控制，2021，49（13）：53-63.

[6]杜茂康，張雪，肖玲，等.基于多目標和貝葉斯優化的短期負荷區間預測[J].國外電子測量技術，2023，42（1）：49-57.