應用型本科院校專業需求與《高等數學》課程教學研究

摘 要：應用型本科院校以培養應用型本科人才為目標，其中“高等數學”課程教學必須結合學生所學的專業，將高等數學的知識服務于學生的專業課程，提升學生解決問題的能力。由于專業方向的差異性，應用型本科院校“高等數學”課程宜于采用基礎模塊與拓展模塊相結合的模塊方式組織教學內容。作者從“高等數學課程”教學現狀出發，分析目前應用型本科院校高等數學課程問題，提出教學內容模塊化、建立專業案例庫、加強教師對所教專業知識的學習、增加數學實驗內容、融入數學建模思想、實現案例教學等措施和方法，以此來滿足學生所學專業對高等數學知識的需求。

關鍵詞：應用型本科院校;高等數學;專業需求

中圖分類號：G642.0 " " " " " " " " " " " " " " " " " " " " " " " " " 文獻標識碼：A 文章編號：1009-3583（2024）-0128-04

Research on the Professional Requirements of Applied

Undergraduate Colleges and the Teaching of Higher

Mathematics Course

LU Mei-hua， ZHANG Yun-xia

（Jiangxi University of Technology， Nanchang 30096， China）

Abstract： Applied undergraduate colleges aim to cultivate applied undergraduate talents， and the teaching of “Higher Mathematics” courses must be combined with students’ majors， serving students’ professional courses with knowledge of higher mathematics and enhancing their problem-solving abilities. Due to the differences in professional directions， the “Higher Mathematics” course in applied undergraduate colleges is suitable for organizing teaching content using a modular approach that combines basic and extended modules. This article starts from the current teaching situation of “Higher Mathematics” courses and analyzes the problems of higher mathematics courses in applied undergraduate colleges. It proposes measures and methods such as modularizing teaching content， establishing a professional case library， strengthening teachers’ learning of the professional knowledge taught， increasing mathematical experimental content， integrating mathematical modeling ideas， and implementing case teaching to meet students’ professional needs for higher mathematics knowledge.

Keywords： applied undergraduate colleges; higher mathematics; professional requirements

歐美大學的課程一般是按知識自身的體系設 置，即使是應用性的課程設置，歐美大學也更多地以 問題為導向而較少陷入教學行政性管理形成的桎 梏。特別是在以數理理論為基本支撐的工科應用型 專業中，以專業發展需求為依據的數學課程內容選 擇更是基于專業知識底層體系而優化裁剪的。另 外，即使在知識屬性上確實存在著自然科學和社會科學的分野，但這些學科知識中內嵌的科學精神本 質上是一致的。這在歐美的專著、學分自選課程和 教師指定必讀著作、選讀著作中都有體現，例如《微 積分學的衰落——離散數學的興起》《選舉幾何學》、 《社會科學中的數學和其他論文》。

但是，我國《高等數學》課程體系相比較于歐美1983年已開始的課程更新[1]，其課程體系和授課內容是相對陳舊與落后的[2]。我國當前興起的“新工科”“新文科”“應用型本科”等教育革新思想更對作為基礎支撐的《高等數學》課程體系與教學實踐提出了迫切的內容更新、模塊化設置的要求。為此，本文以《高等數學》課程為研究對象，首先分析了目前應用型本科院校該門課程的教學現狀，提出了教學內容模塊化、建立專業案例庫、加強教師對所教專業知識的學習、增加數學實驗內容、融入數學建模思想、實現案例教學等措施和方法，以此來滿足學生所學專業對高等數學知識的需求。

1"" 高等數學的教學現狀

1.1" 我國高等數學課程體系陳舊

我國的高等數學教學現狀復雜多維，特別是大高等數學涉及課程體系、教學內容、教學方法、學生參與度、教師素質以及政策支持等多個方面。從課程的教學體系上，大高等數學課程通常包括微積分、線性代數、概率論與數理統計等核心內容。然而，隨著科技的發展和社會的進步，高等數學的教學內容也在不斷更新和擴展，以適應新時代的需求。同時，我國一些高校即使在嘗試引入跨學科的教學內容，以培養學生的綜合素質和創新能力，但部分高校有以行政管理劃分課程而非以知識的自然關系和發展關系劃分課程的傾向。歐美大學中的課程設置一般是基于知識自身自發的體系化自然而然的分界而成，從而在應用性系列的課程設置中更多的是以問題為導向而較少以教學管理為導向，由此歐美高等數學課程很早就實行了教學內容的更新。安東尼·羅爾斯頓，朱惠霖早在1983年在《微積分學的衰落 ——離散數學的興起》提出了高等數學內容的更新。 總體上比較而言，我國高等數學課程體系是相對陳 舊的[3]。

1.2" 教學中存在問題

教學內容與專業脫節。由于高校的數學課程教師大多是數學專業的畢業生，特別是當前高校為了提升師資學歷比水平，大批量非師范畢業的數學專業研究生進入教學體系，其教材理論體系、教學編制或選擇都受到其教育背景的影響，其側重點大多偏向理論而缺乏實踐應用考量，一些教師因“自我專業背景”而選擇“自我偏好”的教材，由此導致教學與學生的專業屬性和學生的學業需求存在一定脫節。特別是應用型本科高校中教學內容多，高等數學教學課時量少，上課節奏較快。一方面，高等數學課程體系龐雜，知識點繁多，教學任務普遍偏重；另一方面，高等數學課程內在的邏輯性、自身的抽象性和論證嚴密性又導致了學生學習困難。高等數學教師普遍反映要把高等數學課程講實講透徹需要一定量課時保證。但是大多數應用型本科院校都非常重視學生專業課程的學習以及學生的實訓實習，對數學課程的學習不夠重視，覺得可有可無。為了增加專業課的課時，高數的課時往往會被壓縮，課時比較緊張，無法有效保證教學任務的完成。

1.3" 高等數學教學需求

高等數學是大學教育中的一門重要基礎課程，它要求學生掌握扎實的數學基礎知識和基本技能，其主要內容包括微積分、向量代數、空間解析幾何、無窮等。這些知識和技能是后續課程學習和科學研究的基礎，也是未來職業生涯中必不可少的工具。隨著我國經濟的快速發展和科技進步，對創新型人才的需求越來越迫切。因此，高等數學教育應當注重培養學生的創新能力和強調思維方式，通過啟發式教學、問題導向學習方式等，激發學生的好奇心和求知欲，培養其獨立思考和解決問題的能力。高等數學尤其要提升應用能力，高等數學不僅僅是一門理論學科，它還有廣泛的應用。在教學過程中，應當注重培養學生的應用能力，通過案例分析、實驗實踐等方式，讓學生將數學知識與實際問題相結合，提高其在專業領域內的應用能力。

高等數學要求專業支撐性。一方面，應用型本科高校中的學生差異性、專業差異性都要求個性化學習的支持。同時，不同學生的學習需求和興趣也存在差異，因此高等數學教學應當注重個性化學習。具體通過分層教學、選課制度等方式來滿足不同學生的學習需求；通過開設選修課程、組織學術講座等方式，拓寬學生的知識視野和興趣愛好。另一方面，信息技術的融合可以支撐高等數學與專業的融合性。隨著信息技術的快速發展，多媒體和網絡技術已經廣泛應用于高等數學教學中。這不僅可以提高教學效率和質量，還可以激發學生的學習興趣和積極性。因此，高等數學教學應當充分利用信息技術手段，改革教學方式和方法，提高教學效果，提升教學水平，以此來適應各類應用型本科專業對高等數學教學的差異性要求。

2"" 課程更新和體系重構

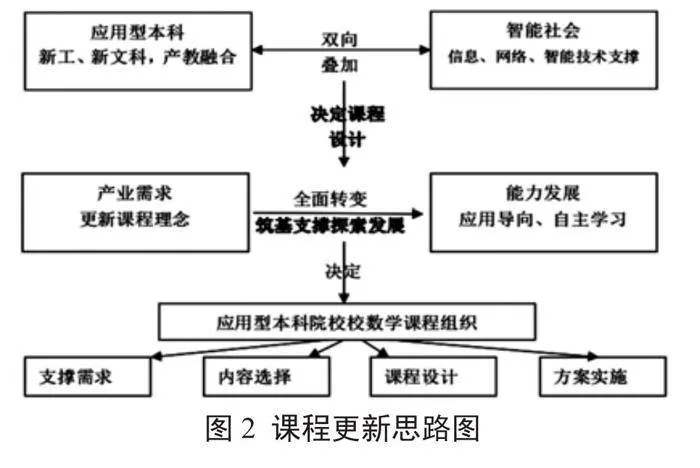
2.1" 課程更新體系重構思路

借鑒外部經驗，美國傳統微積分內容和理論深度雖然比我國的淺顯，但涉及知識面和應用領域較寬，它是以微積分為主線組織起來的大高等數學課程體系，并且便于自學，能開闊學生視野，活躍思維；教材中習題類型多數量大，著眼于讓學生從自主學習中獲取知識，有助于因材施教和學生的個性化發展。美國國家科學基金會在1987年提出的“微積分學課程需要修正與更新”的建議中強調應著重培養學生“概念的理解能力，解決問題的技巧，分析與舉一反三的技能，實行新方法，減少冗長乏味的計算”。

為此，在應用型本科高校中，應按照現代產業、工程技術中的需要、數理知識體系，以“數理知識的組織結構和特征”來決定“新學科和產教融合背景下”數理課程的設置和教學。按照為各類應用型高校提供能支撐不同專業方向的大學數學課程的指導方針，借鑒歐美高等數學內容更新的經驗，將現代數學理論部分擴充為高校數學內容，在大學數學中添加離散數學、科學邏輯等知識，形成以知識應用、能力培養的大學高數課程；這樣，既擴充了高等數學中離散性數理知識，又更新了原來以應用導向式的數學課程為“運用現代軟件”和實現“實踐能力培養”導向的高數體系。

2.2" 課程內容更新方法

一方面，研究著名學者的經典著作，并分析各類專業主干課程教材，從中提煉出適合新工科、新文科、符合產教融合的共性數理知識。具體遵照現代產業、工程技術的需要、數理知識體系構造以形成整體性數學。

總之，提取各類需要學科的著名學者、重要專著中用到的共識性數理知識。例如，從錢學森的名著《系統工程引論》，哈爾濱工業大學的現代數學系列教材，工程力學、彈性力學，動漫制作，Matlab軟件等中提取教學所需要的基礎數學知識；或者從《拓撲心理學》《社會物理學》《政治博弈論》等經典中提取共性數理知識[4-6]。對工程學科、軟件科學、經濟學科、管理學科提取的共性數學知識進行分類，采用現代數學觀點加以整理，把線性結構、拓撲結構、計算算法等現代數學觀點嵌入高等數學之中，對這些數理知識的體系化、邏輯重構、概念再構造，為當前“擴充應用導向的、實踐導向的課程”需要而形成可自主發展的高數知識基礎。

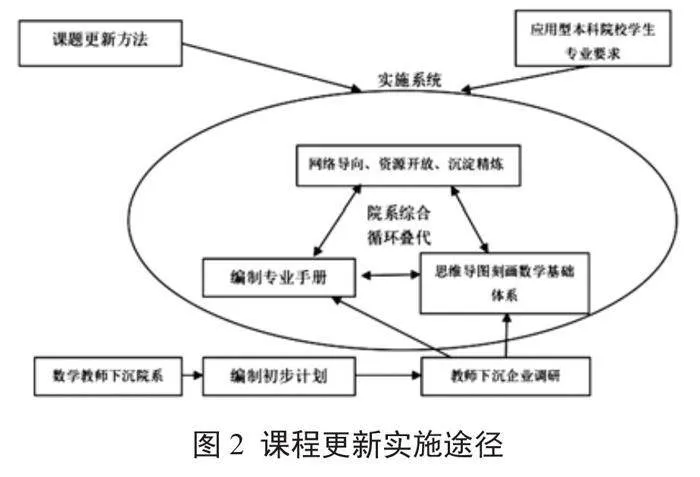
2.3" 課程構造更新和實施路徑

課程更新構造路徑主要有兩個方面，一個方面是按照現代工程技術發展、智能技術發展，破除以解題和計算能力為基礎的數學體系，形成現代數學知識體系，并“提升計算能力為運算能力”，形成“構圖能力、邏輯能力、結構化知識體系的能力”；另一個方面基于線上各類自主學習資源，編制指導學生自主學習的方法等手冊，如編制基本工程技術計算中要用到的微分、積分、優化計算方法手冊；編制工程產業中經常用到的技術常數手冊；直接靠攏“產教融合”等目標。其次，在應用型本科高校中基于體系化、靠攏“新學科背景、產教融合等目標”的共性數學知識前提下，對學生各類網絡自主學習資源，研究分層、分類，研究在新工科、新文科、產教融合等背景更新高數內容后的相關考核方案，以形成性考核評價替代傳統的命題考試考核方式。因此具體的教材教案編制，應以特定高校為案例，為其全部學生提供基礎性數理科學的學習材料和進一步深入到各自專業方向所需要的具體學習材料。針對前者，形成該校自己的特色教材，針對后者凝練出各個專業方向下的參考閱讀材料，開列出相應的書單。

3" 學生專業需求與《高等數學》相結合措施和課程模塊方法

依托課程更新體系重構思路，并結合課程內容更新的具體方法，尤其是按照課程構造更新和實施路徑，從教學的實踐經驗出發，用以下策略實現學生專業需求與《高等數學》相結合。

3.1 總體方法

按應用型專業需求，建設“知識小超市“，實現模塊化教學，將公共基礎課程屬性的高等數學設置在大學一年級，夯實學生數學基礎，培養應用型人才。高等數學課程中，一方面強化數學相關的知識概念，強化概念的客觀背景，提高邏輯思維能力訓練而弱化簡單性程序性計算要求；另一方面，提高學生利用數學解決問題的能力，同時為學生的后續重要專業課程的學習打下堅實的數學基礎[7、8]。以應用型本科院校培養應用型的人才為準繩，重組傳統數學內容，特別強調實踐應用方面的聯系，緊密結合學生專業需求，打破原有的教學體系，以具體專業學生后續課程需要的數學知識來組織教學內容，根據專業教學目標設計教學模塊。例如 “人文模塊”中可引入數學史， 激發學習興趣，解決“學什么”“為什么學”“怎樣學”這三個問題。其中，基礎模塊應綜合不同專業對共性知識的需求進行設置，淡化數學結論推導過程，強化概念的直觀理解。如“計算能力模塊”訓練學生計算能力，“應用模塊”主要解決“有什么用”、“什么時候用”、“怎么用”三個問題。

另外，按不同專業需求，重新組織大高等數學內容為通識模塊、專業服務模塊、個性化教學模塊。通識模塊可涵蓋微積分、線性代數、概率統計等基本知識，著重構建基礎知識體系，為所有專業的必修基礎模塊；專業服務模塊以專業具體需求和知識聯系為導向，突出專業應用所必需的知識模塊；“個性化教學模塊”則以提高數學技能為宗旨，強化考研等競爭選拔方面數學技能。

3.2"" 具體方法

3.2.1" 結合專業方向建立針對性案例庫。提高案例教學法水平，保障高等數學知識與專業方向知識有機融合，以專業背景輔助提升學生高數知識運用與問題解決的能力。其中案例教學務必有專業背景，建立專業案例迭代更新機制，并保障專業案例庫可自學性與授課性的結合。 利用有針對專業差異性的案例。破解任課老師數學知識與學生專業所需要數學知識的隔閡，反過來以此引導教師查閱學生專業課程教材，尋找師生結合點，收集專業教學案例，建立充足的、適應專業差異性的案例庫，真正落實差異性高數教學。

3.2.2"" 強化任課教師的專業知識學習，提高教學能力。破解當前高等數學課程教師的單純數學專業出身、數學背景與學生專業多樣性差異性的矛盾。要求激發并強化任課教師學習各專業背景知識的熱情，引導授課教師分析學生專業需求，發展需求，在底層邏輯上為學生塑造專業底色，做到將學生專業知識與數學知識有機融合，即對學生要用到的數學基礎了然于心，又能用學生易于接受的方式精講細練，滿足學生專業課程需求。

3.2.3"" 增加數學實驗，培養實踐能力。破解傳統課堂教學中教師專注于數學解題、定理證明、公式推導的弊端，充分運用現代信息技術手段，豐富課堂教學的視覺、聽覺體驗性，豐富空間體驗性，豐富動手操作性。當前計算機技術快速發展，智能手機廣泛運用，各類小程序和越來越多數學軟件十分便利，如 Matlab、Mathematics、Maple等，數學實驗和動手實踐越來越方便可行，因此高等數學可適當增加數學實驗，培養學生實踐能力。

3.2.4融入數學建模，提升學生解決實際問題的能力。 當前的高等數學課堂授課中，公式的推導及例題的 計算占用了大部分時間，但概念教學占用時間較少， 導致學生理解概念不到位，其后果是學生應用數學 知識解決實際問題的能力十分欠缺，數學修養、數學 素質未得到提升。如在微積分的積分學講解中，以 考試獲得學分為目的，授課教師以定積分計算為重 點而忽視定積分概念的深入分析，學生可能學會了 簡單積分計算，但遷移到具體專業實際的問題中，積 分工具卻完全無法應用，使得高等數學對專業學習 的支撐作用甚微。為破解這一矛盾，可引入數學建 模思想，透徹講授基本概念并以數學建模工具把學 生專業背景下的問題數學模型化，然后采用數學軟 件加以解決，以動手和動腦相結合的方式進行教學， 以專業需求為導向進行教學，以回歸基本概念搭建 知識體系進行教學，共同破解傳統應試和學分導向 的教學。

3.2.5" 創新教學方法，采用數學史激發學生學習興趣。高等數學中的一些概念、定理非常抽象，特別是其知識體系的編撰過程與其歷史發展過程可能完全顛倒，其知識體系的嚴謹性會抵觸實踐思維而不利于實踐。例如，在數學實踐中并無不定積分的位置，但定積分的實踐背景遠遠超越極限導數等，微積分的源頭本質上在定積分，基于定積分去弱化“形式化的不定積分”尤為重要。為此，創新教學方法，采取歷史背景疏通數學實踐的斷點，既可以利用數學歷史激發學生學習興趣，也可以利用數學實踐化解學習難點。顯然，在定積分的背景下不定積分毫無難度，僅僅是輔助性計算。由此，創新教學方法，采取歷史背景，就能化解學生學習“一些形式性理論”中的理解困難，加深學生對概念的準確理解和深刻記憶，形成后續專業學習的真正支撐。

4" 結語

本文從《高等數學》支撐不同學生不同專業的發展需求出發，分析了目前應用型本科院校該課程的教學現狀，其該現狀決定了高等數學教學需要更新教學內容和重構課程體系。為此，作者提出高等數學教學上應實施教學內容模塊化、建立專業案例庫、加強教師對所教專業知識的學習、增加數學實驗內容、融入數學建模思想、實現案例教學等措施和方法，以滿足學生專業對高等數學知識的需求。

另外，為破解高等數學教學教師數學知識陳舊的局面，破解“高等數學教學和各專業脫節”及“高等數學只能提供學分而不能為各專業提供支撐”的僵化局面，應用型本科高校應該提升教學水平，形成適合各專業學生的課程體系并進一步提升高等數學課程的開放性，推動高數課程的融合與分離。一方面，課程融合就是在既定的課時限制下，充分融合數學知識的講授。另一方面，課程的分離又是就不同基礎水平的學生提供合適水平的課程。

當然，基于現代數學學科為“建設高質量教育體系”提供支撐的基礎性地位，即依托現代數學觀念培養具有邏輯嚴謹、能獨立思考并敢于在工作實踐中開拓的學生；應用型本科高校更應該創新高等數學的教學方法、教學手段，提高高等數學的教學水平和教學質量。

參考文獻：

[1]安東尼·羅爾斯頓，朱惠霖.微積分學的衰落——離散數學 的興起[J].世界科學，1983（10）：7-10.

[2]肖春梅，黃春妙，蘇安.與專業同向同行的理工科“高等數學” 課程教學改革與創新研究[J].教育教學論壇，2024（2）：73-76.

[3]王麗美，宋乃慶.近二十年中國數學教育研究的熱點主題 ——基于科學知識圖譜的實證分析[J].數學教育學報，2022， 31（5）：65-70.

[4]萊溫.拓撲心理學[M].寧波：浙江教育出版社，1997.

[5]劉怡君. 社會物理學：社會治理[M].北京：科學出版社，2014.

[6]麥卡蒂，梅羅威茨.政治博弈論[M].上海：格致出版社上海三 聯書店，2009.

[7]胡衛群，盛立人，肖箭.選舉幾何學[M].北京：科學出版社， 2011.

[8]盛立人.社會科學中的數學[M].北京：科學出版社，2006.

[9]阿萊克斯 彭特蘭.智慧社會：大數據與社會物理學[M].寧波：浙江人民出版社，2015.

[10]（美）蔣中一，（加）凱爾文·溫賴特.數理經濟學的基本方法[M].北京：北京大學出版社，2006.

（責任編輯：羅東升）