Wolfe線搜下改進的FR型譜共軛梯度法

摘 要：譜共軛梯度法作為經典共軛梯度法的推廣，它是求解大規模無約束優化問題的有效方法之一.基于標準Wolfe線搜索準則和充分下降性條件，提出了一種具有充分下降性質的FR型譜共軛梯度法.在溫和的假設條件下，該算法具有全局收斂性.最后，將新算法與現存的修正FR型譜共軛梯度法進行比較，數值結果表明提出的算法是極其有效的.

關鍵詞：無約束優化；譜共軛梯度法；充分下降性；標準Wolfe線搜索準則；全局收斂性

中圖分類號：O221.2 " " " " " " " " " " " " " " " " " " " " " " " " " 文獻標識碼：A " "文章編號：1009-3583（2024）-0080-05

FR Type Spectral Conjugate Gradient Method Improved

by Wolfe Line-search

（WANG Sen-sen1， HAN Xin2*， WU Xiang-biao3

（1.School of Mathematics and Information Science， Xinjiang Hetian College， Hetian 848000， China; 2. School of Mathematics， Sichuan University of Arts and Sciences， Dazhou 635000， China; 3. School of Mathematics， Zunyi Normal University， Zunyi 563006， China）

Abstract： The spectral conjugate gradient method， as an extension of the classical conjugate gradient method， is one of the effective methods for solving large-scale unconstrained optimization problems. Based on the standard Wolfe line search criterion and sufficient descent condition， a FR type spectral conjugate gradient method with sufficient descent property is proposed. Under mild assumptions， the algorithm has global convergence. Finally， the new algorithm is compared with the existing modified FR type spectral conjugate gradient method， and numerical results show that the proposed algorithm is extremely effective.

Keywords： unconstrained optimization; spectral conjugate gradient method; sufficient degradability; standard Wolfe line search criteria; global convergence

共軛梯度法作為一種優化方法，憑借其算法結構簡單、易于編程和存儲需求少等特點，常被用于解決航空航天、大氣模擬、石油勘探、信號恢復等工程應用領域遇到的大規模優化問題[1-4].共軛梯度法 （Conjugate Gradient Method），簡稱CG法，最早是由Stiefel和Hestenes在求解非線性方程組時提出的算法，1962年Reeves和Fletcher將此方法應用于解決非線性優化問題。無約束優化問題是優化領域一類重要問題，其一般形式為

3" 數值實驗和結論

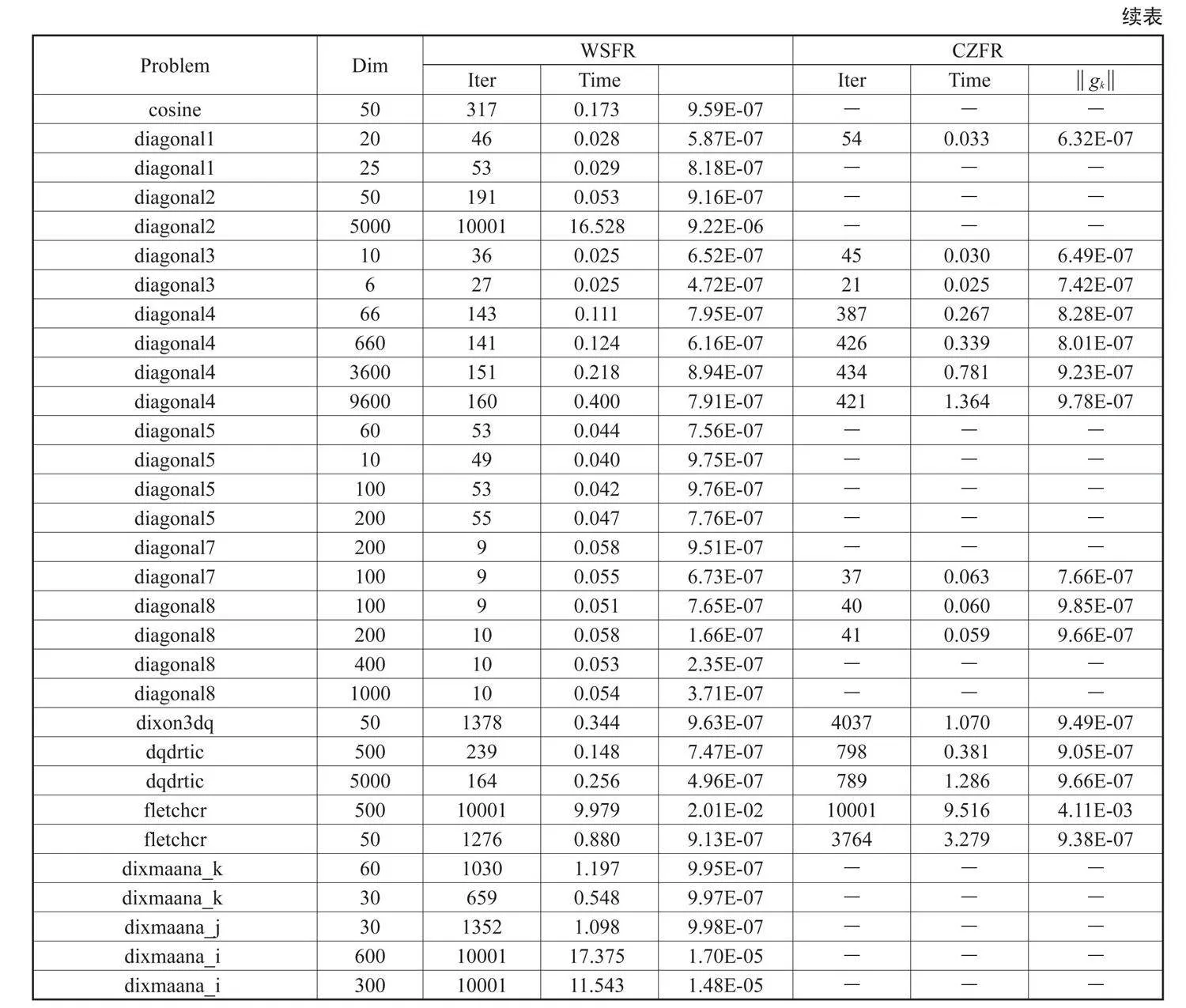
為了檢驗算法WSFR的數值效果，從常見的無約束優化測試函數集中選取部分函數進行測試，并與文獻[22]中的CZFR算法進行數值比較.程序由Matlab編寫，所有算法均在采用Windows 10 操作系統的PC機（榮耀MagicBook，AMD Ryzen 7 3750H with Radeon Vega Mobile Gfx 2.30 GHz）上進行，算法WSFR中參數的設置為：，另外算法CZFR也采用標準的Wolfe線搜索準則確定步長，且參數設置和算法WSFR一致.算法終止準則為或者迭代次數超過10000次.具體運算結果見表1.

表1中，Function：測試函數名稱，Dim：函數的維數，Iter：迭代終止時算法迭代的總次數，Time：算法的CPU運行時間，gk 為迭代終止時目標函數的梯度值，“-”表示算法對此問題無效。從表中結果可以看出，算法WSFR對40個測試問題都是有效的，而算法CZFR僅對60%的測試問題有效.此外，對比迭代次數、CPU運行時間、迭代終止時目標函數的梯度值，40個測試問題中對于兩個算法都有效果的24測試問題而言，算法CZFRR僅有兩個測試問題在迭代次數、CPU運行時間、迭代終止時目標函數的梯度值優于算法WSFR.然而，對于剩下的測試問題，算法WSFR在迭代次數、CPU運行時間、迭代終止時目標函數的梯度值等方面優于算法CZFR.

綜上所述，算法WSFR對比算法CZFR其數值計算效果有明顯的提升，且該算法在標準的Wolfe線搜索準則下具有充分下降性.此外，對于不同的測試問題，算法WSFR可以通過調整譜系數中的參數 來提高數值計算效率.

參考文獻：

[1]王森森，張俊容，韓信，等.一類具有充分下降性的混合型譜共軛梯度法[J].西南大學學報（自然科學版），2017，39（5）：139-144.

[2] Han X， Zhang J， Chen J. A New Hybrid Conjugate Gradient Algorithm for Unconstrained Optimization[J]. Bulletin of the Iranian Mathematical Society，2017，43（6）：2067-2084.

[3] 鄭宗劍， 韓信. 一種具有充分下降性的新混合型共軛梯度法[J]. 西南師范大學學報（自然科學版）， 2022， 47（1）： 1-7.

[4] 陸游，何嘉.基于并行優化與訪存優化遺傳算法的TSP問題求解方法[J].四川文理學院學報，2017，27（2）：11-17.

[5]Fletcher R， Reeves C M. Function Minimization by Conju-gate Gradients[J]. The Computer Journal， 1964，7（2）：149-154.

[6] Dai Y H， Yuan Y. A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property[J]. SIAM Journal on Optimization，1999，10（2）：177-182.

[7] Fletcher R. Practical Methods of Optimization Unconstrained Optimization[J]. Journal of the Operational Research Society，1980，33（7）：675-676.

[8] Hestenes M R， Stiefel E. Methods of Conjugate Gradients for Solving Linear Systems[J]. Journal of Research of the Nation-al Bureau of Standards， 1952， 49（6）： 409-436.

[9] Polyak E， Ribiere G. Note Sur La Convergence De Méthodes Directions Conjuguées.[J]. Revue Francaise Informatique Et De Recherche Opérationnelle， 1968，3（16）：35-43.

[10]Polyak B T. The Conjugate Gradient Method in Extremal "Problems[J]. Ussr Computational Mathematics amp; Mathemat- ics Physics，1969，9（4）：94-112.

[11] Liu Y， Storey C. Efficient Generalized Conjugate Gradient" Algorithms.Part1：Theory[J]. Journal of Optimization Theory" and Applications，1992，69（1）：129-137.

[12] Wei Z X， Yao S W， et al. The Convergence Properties of "Conjugate Gradient method for Optimization[J]. Appl Math "Comput，2006，183（2）：1341-1350.

[13] Yao S W， Wei Z X， et al. A Note about WYL’s Conjugate "Gradient Method and its Application[J]. Applied Mathemat- ics and Coumpuation，2007，191（2）：381-388.

[14]林穗華.改進共軛梯度法的收斂性[J].西南大學學報（自然 科學版），2021， 43（7）：81-88.

[15] Wang Y， Huang J P， Shao H， et al. A Modified PRP-HS hy- brid Conjugate Gradient Method with Global Convergence[J]. "Mathematical Theory and Applications，2022，42（4）：58-70.

[16] 張鵬，杜學武.強Wolfe線搜索下一種混合的PRP-WYL 共軛梯度法[J].重慶師范大學學報（自然科學版），2020，37（1）： 41-51.

[17] Birgin E G， Martinez J M. A Spectral Conjugate Gradient "Method for Unconstrained Optimization[J]. Applied Mathe- matics and Optimization，2001，43（2）：117-128.

[18] 劉鵬杰，江羨珍，宋丹.一類具有充分下降性的譜共軛梯度 法[J].運籌學報.2022.26（4）：87-97.

[19] 江羨珍，廖偉，簡金寶，等.一個帶重啟步的改進PRP型譜共 軛梯度法[J].數學物理學報，2022，42（1）：216-227.

[20] 簡金寶，劉鵬杰，江羨珍.一個充分下降的譜三項共軛梯度 法[J].應用數學學報.2020，43（6）：1000-1012.

[21] 王森森，張俊容，韓信.一類修正的FR型譜共軛梯度法[J]. 西南大學學報（自然科學版），2018，40（2）：49-55.

[22] 晁麗佳，張永富.修正FR型譜共軛梯度法在信號恢復中的 應用[J].重慶師范大學學報.2023，40（5）：11-18.

[23] Zoutendijk G. Nonlinear Programing Computational Me- thods[J]. Integer and Nonlinear Programing.1970，143（1）：37- 86.

[24] 劉鵬杰， 吳彥強， 邵楓，等.兩個帶重啟方向的改進HS型共 軛梯度法[J].數學物理學報，2023，43（2）：570-580.

[25] Andrei N. An Unconstrained Optimization Test Functions "Collection[J]. Advanced Modeling and Optimization，2008， 10（1）：147-161.

（責任編輯：羅東升）