讓探究之花在解題教學中精彩綻放

［ 摘 要 ］探究是開啟學生智慧的鑰匙，是提高課堂教學有效性的重要手段.教學中，教師要為學生營造一個良好的探究環境，重視發揮學生主體和教師主導的作用，通過“一題多變”打開探究之門，讓探究之花綻放課堂，點亮人生.

［ 關鍵詞 ］探究；一題多變；綻放課堂

解題是數學教學的重中之重.在傳統教學中，部分教師常把數學教學定義為解題教學，可見解題在數學教學中的價值.如何培養和提高學生的解題能力是一個經久不衰的熱點話題.筆者認為，在解題教學中，教師應少一些“灌輸”，多一些“探究”，引導學生通過觀察、實驗、探索、交流等活動主動發現問題、提出問題、解決問題，以此促進學生解題能力的提升和思維能力的發展.筆者以復習課中一道典型探究題為例，談談自己對解題教學的幾點認識，供同行參考.

教學過程

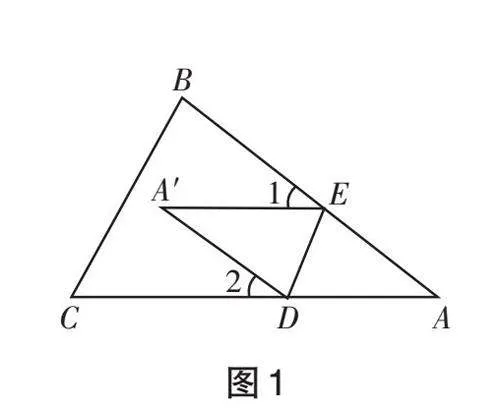
環節1 問題呈現例1 如圖1，將 △ABC 紙片沿DE 折疊，使點 A 落在四邊形 BCDE內部 A' 的位置，則 ∠1 + ∠2 與 ∠A'之間存在怎樣的數量關系？說一說你的理由.（問題①）

問題①給出后，教師沒有急于讓學生解答，而是鼓勵學生“折一折”“畫一畫”“說一說”.教師在巡視中發現，大多數學生嘗試從四邊形和三角形內角和中尋找解題的突破口，通過有效互動解決了這個探究問題，但是也有少數學生陷入了沉思，他們迫不及待地想知道解決問題的方法.此時，在學生渴望求知的氛圍中，教師帶領學生走上探究之旅.

設計意圖 例題呈現后，教師沒有急于講授，而是讓學生通過動手實踐和合作交流探究解決問題的方法，以此提高學生參與課堂的積極性，激發學生探究欲.

環節2 合作探究

師：現在請大家在原來的紙片上繼續“折一折”，改變點 A' 落在四邊形 BCDE 內的位置，此時 ∠1 ，∠2 和 ∠A' 的大小發生了怎樣的變化呢？（問題給出后，學生積極操作、觀察、思考、交流）

生 1： ∠A' 的大小始終保持不變， ∠1 和 ∠2 的大小是發生變化的，當 ∠1 變大時 ∠2 變小，當 ∠2 變大時∠1 變小.

教師利用幾何畫板進行動態演示，讓學生進一步觀察，獲得更加直觀的感受.

師：大家想一想，點 A' 除了落在四邊形 BCDE 的內部外，還可以落在什么位置呢？請大家試一試.學生積極動手操作，很快就有了新的發現，迫不及待地展示自己的操作成果.

生 2： 點 A' 可 以 落 在 點 B 或點 C 上.

生 3： 點 A' 可 以 落 在 四 邊 形BCDE 的四條邊上.

生 4：點 A' 還可以落在四邊形BCDE 的外部.

……

師：大家真棒.結合大家的發現想一想，以上各種情況是否可以分類呢？

生5：可以分成3類，即點 A' 分別在四邊形 BCDE 的內部、外部和邊上.

師：非常好，點 A' 在四邊形BCDE 的內部的圖形已經有了 （如圖1），如果讓你將另外兩種情況用圖形表示出來，你會嗎？

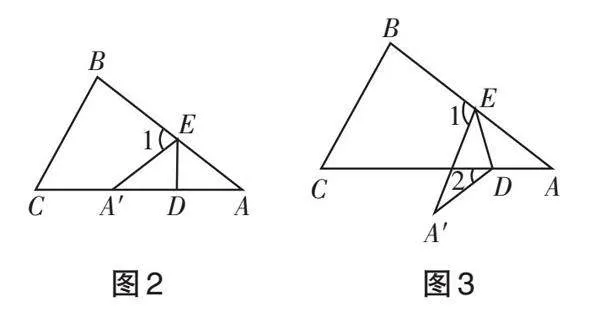
學生積極思考，通過觀察、比較、歸納，畫出了另外兩種類型的圖形（如圖2、圖3）.

師：圖2中， ∠1 與 ∠DA'E 有怎樣的數量關系呢？說一說你的理由.（問題②）

該問題不難，教師讓學生自主探究，然后點名讓學生板演證明過程，教師點評.

師：大家利用三角形外角的性質輕松地得到了答案，即∠1=2∠DA'E.

師：問題①和問題②存在怎樣的異同呢？（教師預留充足時間讓學生觀察、思考）

生 6：它們都是將 △ADE 沿 DE折疊，不過點 A 的落點不同，問題①中點 A 落在四邊形 BCDE 內部，而問題②落在四邊形 BCDE 邊上.

生7：問題①中的 ∠A' 和問題②中的 ∠DA'E 都與 ∠A 相等.

生8：圖形不同，所求的結論也不同，問題①所研究的是 ∠1 + ∠2 與∠A' 之間的數量關系，而問題②研究的是 ∠1 與 ∠DA'E 的數量關系.

生9：圖2中 ∠1 是 △AEA' 的外角 ， 所 以 有 ∠1=∠DA'E + ∠A ， 又∠DA'E = ∠A ，故 ∠1 = 2∠DA'E .圖 1中， ∠1 和 ∠2 是四邊形 A'DAE 的外角，結合四邊形內角和有 2∠A' +180° - ∠1 + 180° - ∠2 = 360° ， 故∠1 + ∠2 = 2∠A' .

……

師：大家都說得非常好，若問題①也想運用三角形外角的性質來求解，可以怎么轉化呢？（生積極思考）

生10：連接 AA' ，則 ∠1 ， ∠2 分別轉化為 △AEA' 和 △ADA' 的外角.

師：很好，如果現在運用三角形外角的性質來探究問題①，你會嗎？

結合剛剛的研究經驗，學生很快給出了第二種解法.接下來，教師結合學生給出的兩種解法進行點評.一種解法是之前學生采用的三角形內角和四邊形內角和的解法，還有一種解法是基于問題②的探究經驗，連接 AA' ，利用三角形外角的性質的解法.教師對學生的探究給予充分的肯定與表揚，學生學習積極性高漲.

師：剛剛我們研究了圖 1 和圖2，結合以上探究經驗，你能對圖3中的 ∠1 ， ∠2 提出問題嗎？

在教師的鼓勵下，學生積極觀察、比較、討論、交流，提出了這樣一個問題：如圖 3，把 △ABC 紙片沿 DE 折疊，使點 A 落在四邊形BCDE 外 A' 的位置，則 ∠1 ， ∠2 與∠A' 之間存在怎么樣的數量關系？說一說你的理由.（問題③）

接下來，又開啟了新一輪的探究活動.教師預留充足的時間讓學生思考、探究、交流，教師巡視，并對部分學生進行點撥.接下來，教師投影展示學生的探究過程，并讓學生給出自己的思考過程.

生11：我與剛剛的探究思路相同，連接 AA' ，利用三角形外角的性質把 ∠1 和 ∠2 分別表示出來，然后將 ∠1和 ∠2 作差，即得 ∠1 - ∠2 = 2∠A' .

生12：令AC與A'E相交于點F，則∠1=∠A+∠AFE，∠AFE=∠A'+∠2，故∠1=∠A+∠A'+∠2，又∠A=∠A'，所以∠1=2∠A'+∠2，即∠1-∠2=2∠A'.

設計意圖 在探究活動中，教師充分發揮了教師主導和學生主體的作用，通過啟發與引導讓學生主動將原圖進行拓展，由“點 A' 在四邊形BCDE 內”推廣至“點 A' 在四邊形BCDE 邊上及在四邊形 BCDE 的外部”，這樣通過拓展不僅豐富了課堂教學內容，而且使探究活動更具系統性，有利于學生認知結構的優化和解題能力的提升.在以上探究活動中，教師沒有急于呈現問題①的解題過程，而是借助問題②的解決，引導學生通過遷移找到了另一種解決方法，這樣既提高了學生的解題信心，又讓學生體會了數學知識的內在聯系，有利于學生學習能力的提升.在問題①和問題②解決后，教師又讓學生自主探究問題③，以此通過合作與交流，進一步升華學生的認知，提高學生的解題能力.

環節3 課堂小結

師：經歷以上探究活動，你有哪些收獲？有何感受？

學生積極發言，主動交流自己的所思、所獲，課堂氛圍活躍.

設計意圖：通過小結引導學生反思回顧、總結歸納，以此進一步鞏固已知知識、經驗、方法.同時，通過互動交流，活躍了課堂，提高了課堂教學有效性.

環節4 拓展練習

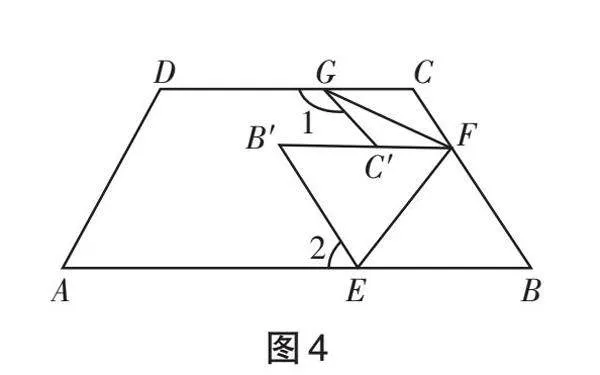
例2 如圖4，把梯形 ABCD 紙片按照如下步驟折疊：①沿 EF 折疊，使點 B 落在梯形 ABCD 內部 B' 位置；②沿 FG 折疊，使點 C 落在 B'F 邊的點 C'位置， B' 與 C' 位置不重合.試探究 ∠1與 ∠2 存在怎樣的數量關系？請說一說你的理由.（問題④）

拓展練習可能會給一些基礎較弱的學生帶來一定的困擾，教師可以先讓他們梳理前面的練習，在有余力的情況下繼續完成拓展練習.對于基礎較好的學生，教師應要求學生認真完成，完成后再幫助有困難的同學一起完成，以此通過合作讓所有學生獲得較大程度的提升.

設計意圖 在原有例題的基礎上，將題目進一步改編，以期在強化認知的基礎上，發散學生的數學思維，提高學生舉一反三的能力.

教學思考

1.關注學生主體價值

在提高學生解題能力的道路上，單靠教師講授是難以達成的，應重視發揮學生的主體性，培養良好的思考習慣.在探究活動中，教師要提供機會讓學生觀察思考、自主探究、合作討論、自我展示，將被動接受轉化為主動獲取，讓學生以“主角”的身份融于課堂，激活思維，提高學生的學習品質.

2.合理引入變式訓練

變式訓練是提高學生解題能力的重要手段，教學中教師應合理引入變式問題，讓學生在“變與不變”中體會數學的魅力，激發學生的探究欲.在以上教學活動中，教師引導學生通過“折疊”發現點 A 可以落在不同的位置，從而運用分類討論的思想將一道題轉化為三道題，使教學內容更加豐富，使學生的認知更加系統.通過變式訓練，讓學生感受一般到特殊再到一般的認知過程，感悟分類、轉化等數學思想方法的價值，幫助學生積累了豐富的活動經驗，促進了學生探究能力和創新能力的提升.

3.尊重學生個體差異

個體的差異在學習過程中是不可避免的，教師要尊重差異，對不同的學生提出不同的要求，保護學生的學習信心，激發學生的潛能，讓不同層次的學生都能有所提升.在以上教學活動中，教師沒有急于講解，而是基于學生的已有認知設計探究活動，引導學生通過合作實現取長補短，充分發揮個體差異的積極作用，讓每個學生都能有所發展，有所成長.

總之，在解題教學中，要摒棄單一的就題論題，為學生提供時間和機會去觀察、去探索、去交流，以此幫助學生積累活動經驗，提高學生的學習品質，提升學生的解題能力.