和直線與圓相關(guān)的文化創(chuàng)新問(wèn)題解析

一、數(shù)形結(jié)合求最值

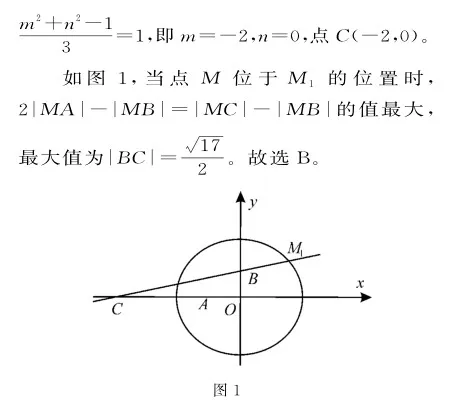
點(diǎn)評(píng)：本題主要考查直線和圓的位置關(guān)系。解決本題的關(guān)鍵是通過(guò)數(shù)形結(jié)合知兩線段距離差的最值是在過(guò)點(diǎn)B、C的直線上。對(duì)于文化創(chuàng)新類(lèi)的平面解析幾何問(wèn)題應(yīng)特別注意數(shù)形結(jié)合思想的應(yīng)用。

二、抓住對(duì)稱性依托數(shù)形結(jié)合求最值

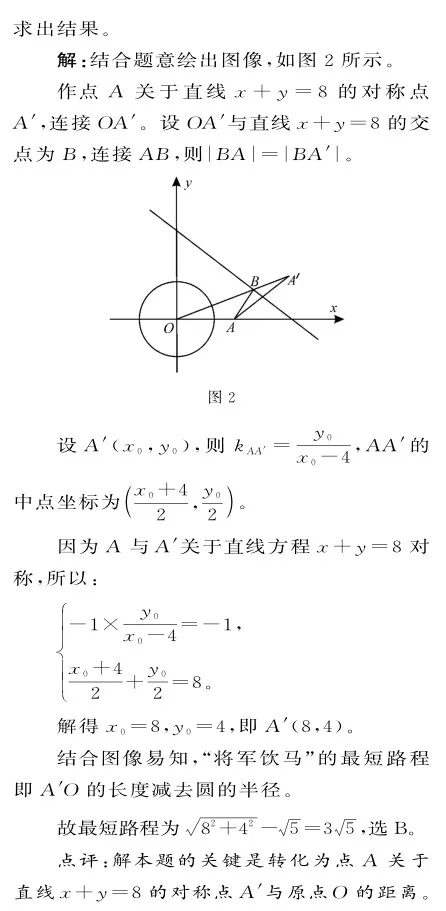
三、依托定義構(gòu)造圓的方程確定直線的斜率

例3 古希臘數(shù)學(xué)家阿波羅尼斯的著作《圓錐曲線論》是古代光輝的科學(xué)成果，其中有這樣一個(gè)命題：平面內(nèi)與兩個(gè)定點(diǎn)距離的比為常數(shù)k（ k>0， k≠1）的點(diǎn)的軌跡是圓，后人把這個(gè)圓稱為阿波羅尼斯圓。已知定點(diǎn)A（ - 2， 0） ， B（ 2， 0） ，動(dòng)點(diǎn)C滿足| A C |= 2 | B C |，則動(dòng)點(diǎn)C的軌跡為一個(gè)阿波羅尼斯圓，記此圓為圓P。已知點(diǎn)D在圓P上（點(diǎn)D在第一象限） ， A D交圓P于點(diǎn)E，連接E B并延長(zhǎng)交圓P于點(diǎn)F，連接D F，當(dāng)∠D F E= 3 0°時(shí)，直線A D的斜率為（ ）。

點(diǎn)評(píng)：本題的解答過(guò)程是先通過(guò)“阿波羅尼斯圓”的定義確定了圓的方程，再觀察圖像，利用題設(shè)條件，最終通過(guò)三角函數(shù)公式的運(yùn)算求出直線的斜率。

（責(zé)任編輯 徐利杰）