考慮土體參數不確定性的新型擋土墻可靠性分析

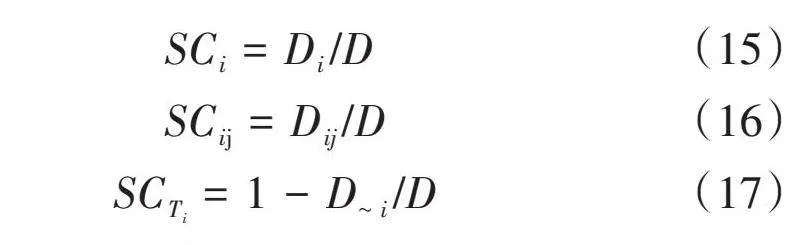
摘 要：【目的】為克服新型擋墻穩定性安全評估中傳統確定性分析存在的缺陷，需要對考慮土體參數不確定性的新型擋土墻可靠性進行分析。【方法】首先，通過概率分布表達巖土參數的不確定性，計算新型擋墻的抗傾穩定和抗滑穩定。其次，通過神經網絡和蒙特卡羅模擬，執行新型擋土墻可靠性分析，定量給出新型擋土墻可靠性指標。最后，通過參數敏感性分析，明確各參數對新型擋土墻安全性影響的重要程度。【結果】結果表明，新型擋土墻穩定性好，但存在一定優化空間，確定性分析結果較為保守。【結論】不同參數對新型擋土墻安全影響各不相同，應準確估計填土內摩擦角，保證擋土墻穩定性。研究成果為新型擋土墻可靠性分析提供了思路和方法。

關鍵詞：新型擋土墻；參數不確定性；可靠性分析；敏感性分析

中圖分類號：P642.22；TV221.2 文獻標志碼：A 文章編號：1003-5168（2024）15-0046-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.15.010

Reliability Analysis of a New Retaining Wall Considering Soil

Parameter Uncertainty

XU Haolun1 ZHANG Yingxue 2

（1.Chongqing Water Conservancy and Electric Power Construction Survey，Design and Research Institute Co.， Ltd.， Chongqing 404100，China; 2. Chongqing 208 Geological Environment Research Institute Co.， Ltd.， Chongqing 404100，China）

Abstract： [Purposes] In order to overcome the shortcomings of the traditional deterministic analysis on the stability safety assessment of the new retaining wall， it is necessary to analyze the reliability of the new retaining wall considering the uncertainty of soil parameters.[Methods] Fristly， this paper expresses the uncertainty of soil parameters through probability distribution and calculates the overturning stability and sliding stability of the new retaining wall. Secondly，through neural networks and Monte Carlo simulations， reliability analysis of the new retaining wall is performed， providing quantitative reliability indicators. Finally， through parameter sensitivity analysis， the importance of each parameter on the safety of the new retaining wall is clearly identified. [Findings] The results indicate that although the new retaining wall has good stability， there is room for optimization， and the deterministic analysis results are conservative. [Conclusions] Different parameters have varying impacts on the safety of the new retaining wall. Accurate estimation of the internal friction angle of the backfill soil should be ensured to guarantee the stability of the retaining wall. The research approach of this paper provides ideas and methods for the reliability analysis of the new retaining wall.

Keywords： new retaining wall; parameter uncertainty; reliability analysis; sensitivity analysis

0 引言

擋土墻是水利工程中常用的支擋結構，其中重力式擋土墻應用最為廣泛。由于重力式擋土墻特殊的受力特性，其存在材料用量大、施工周期長、經濟性欠佳等缺點。而裝配式擋土墻造價低、自重小，預制化生產也縮短了施工周期，符合低碳環保的設計理念。因此，裝配式擋土墻是一種具有競爭力的擋土結構［1］。

擋土墻與土體聯合結構安全問題備受關注。工程上通過安全系數來衡量擋土墻安全性，簡單且易操作。然而，安全系數大于１并不意味著擋土墻不發生失效。因為天然土體在風化、沉降、侵蝕等綜合作用下，土體性質隨著空間位置的變化存在一定的隨機性，這種隨機性為擋土墻安全性評估帶來了極大不確定 ［2］。為合理表征土體特性的不確定性，可靠性設計彌補了確定性計算方法的缺陷，對指導新型裝配式擋土墻設計有著重要意義［3］。

1 研究方法與理論

1.1 新型裝配式擋土墻的構造

根據具體工程需求，對預制塊的形狀進行選擇，通常采用仰斜式構造形式［1］。擋土墻墻背采用預制塊錯位的堆疊方式，預制塊內部通孔，形成貫通通道。在通孔中加入鋼筋后注入砂漿，形成整體的擋土墻結構，以提高擋土墻整體抗拉性能和整體穩定性。

1.2 擋土墻穩定分析及確定性計算

本研究開展擋土墻結構穩定性分析，包括整體抗滑穩定計算、體抗傾覆計算以及墻體基底壓力驗算。傾斜式墻背擋土墻，墻背填土采用非黏性土進行回填。本研究采用庫倫土壓力公式計算墻背土壓力、主動土壓力，見式（1）、式（2），被動土壓力見式（3）、式（4）。

[Ka=cos2（φ-ε）cos2εcos（φ+δ）+[1+sin（φ+δ）（φ-β）cos（φ+δ）cos（ε-β）]2] （1）

[Fa=12γH2Ka] （2）

[Kp=cos2（φ+ε）cos2εcos（φ-δ）+[1-sin（φ+δ）（φ+β）cos（ε-δ）cos（ε-β）]2] （3）

[Fa=12γH2Kp] （4）

式（2）、式（3）中系數Ka和Kp分別為被動土壓力系數和主動土壓力系數。

本研究以抗傾覆穩定、抗滑穩定為研究對象，抗傾穩定安全系數、抗滑穩定安全系數的計算見式（5）、式（6）。

[Ko=MdMo=（Fsinθ）L3+GL2（Fcosθ）L1] （5）

[Kc=f'G+c'A'H] （6）

式中：[Md]、[Mo]分別為抗傾和抗覆力矩；F為墻后土壓力；θ為土壓力方向與水平向夾角；L1為土壓力水平分力的力臂、L2土壓力豎直分力的力臂、L3為墻自重Ｇ的力臂；[G]為擋土墻上垂直水平面荷載的和；[H]為平行墻基荷載的和；f′和c′分別為墻底與基礎的摩擦系數和黏聚力。

1.3 擋土墻穩定分析確定性計算

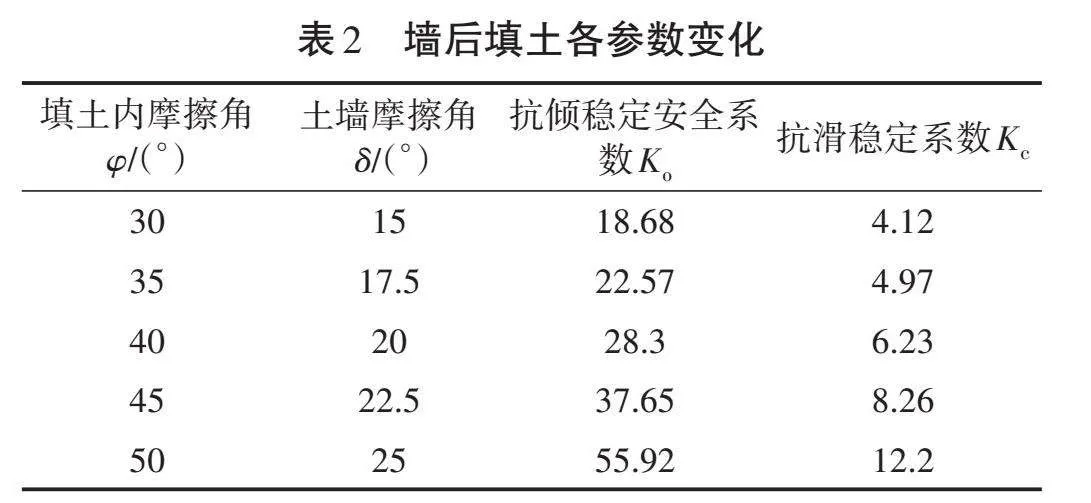
本研究涉及的裝配式擋土墻高為5.4 m，墻背填土高4.5 m。研究表明，土體容重、墻中回填料容重、填土內摩擦角及土墻摩擦角是影響擋土墻穩定性的重要因素。土體容重、墻中回填料容重、填土內摩擦角等參數見表1、表2［2］。

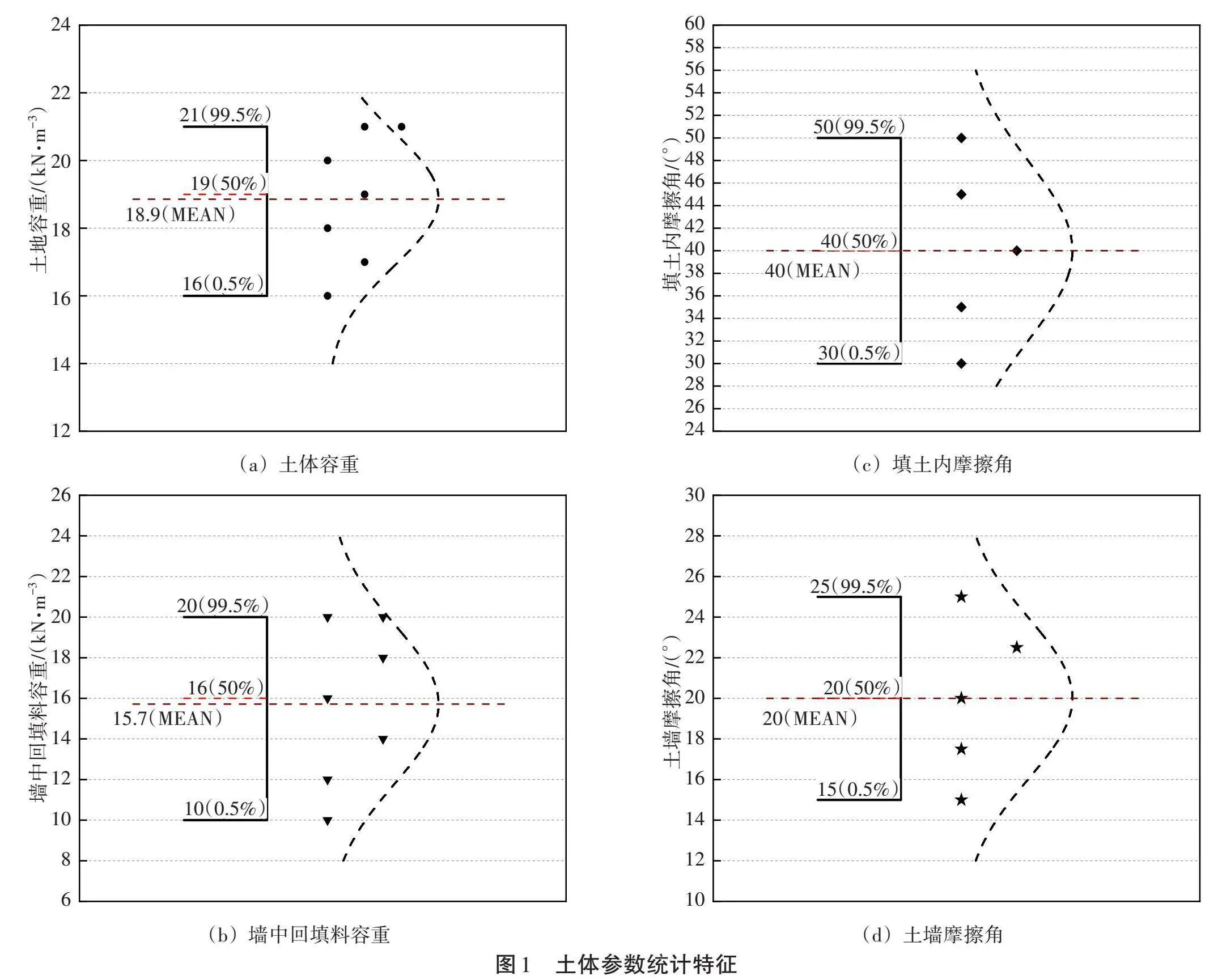
該土體相關參考數據較少，土體相關參數近似正態分布。土體容重近似正態分布N～（18.9，1.55^2），墻中回填料容重近似正態分布N～（15.71，3.05^2），填土內摩擦角近似正態分布N～（40，7.07^2），土墻摩擦角近似正態分布N～（20，3.54^2），具體如圖1

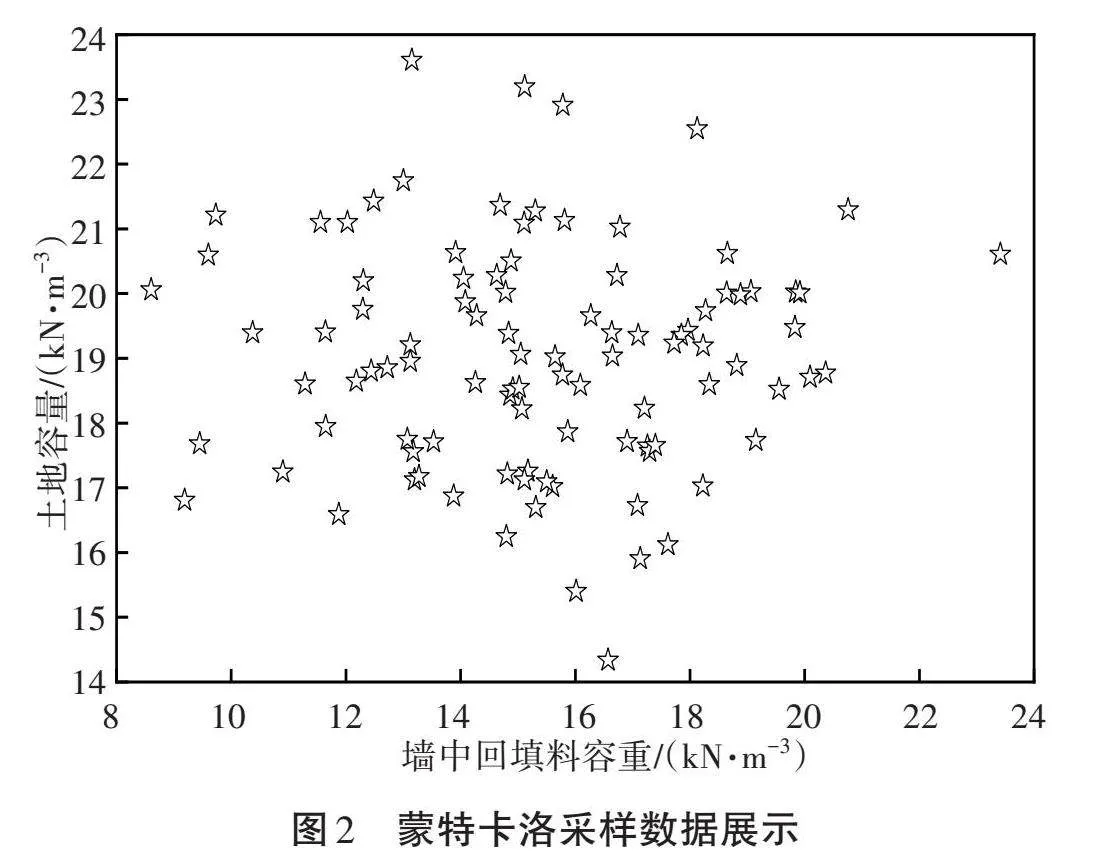
所示。蒙特卡洛采樣生成10 000組數據，以表征土體強度參數不確定性。以土體容重和墻中回填料容重為例，蒙特卡洛采樣100次如圖2所示，可以看

出土體容重和墻中回填料容重覆蓋了參數不確定性區間，能夠反映參數隨機性。

1.4 BP神經網絡代理模型

BP神經網絡是經典的機器學習算法。本研究將表2數據作為訓練數據，訓練基于BP神經網絡的代理模型，替代確定性計算。研究表明，機器學習模型的數據預測精度滿足工程要求。

BP神經網絡正向傳播見式（7），f為sigmood激勵函數［4］。

[fW1X+B1=VW2V+B2=Y] （7）

式中：[W]1為BP神經網絡輸入層到隱藏層的權值矩陣；B1為隱藏層閾值向量；[W]2為隱藏層到輸出層權值矩陣；B2為輸出層閾值向量；X為輸入向量；Y為輸出向量；V為隱藏層輸出值向量。

反向傳播函數見式（8）。

[E=12Ms=1nk=1ysk-osk2] （8）

式中：M為訓練樣本數量；n為輸出層節點個數；[osk]為樣本s在第k個節點的輸出期望；[ysk]為第k個節點輸出。

2 可靠性分析和參數敏感性分析

2.1 可靠性分析

本研究以抗滑穩定安全為例，介紹基于BP神經網絡代理模型的可靠性分析。相關規范要求抗滑穩定系數規范值不小于1.6，構造擋土墻抗滑穩定功能函數見式（9）。

[Z=Kc-1.6] （9）

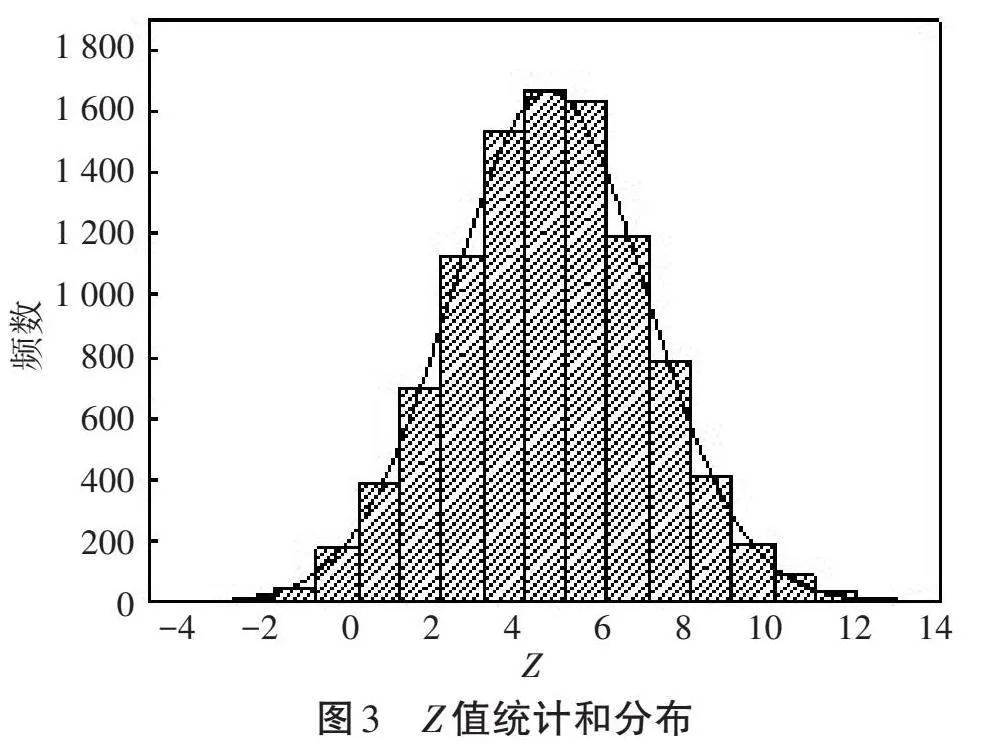
將1.2節中10 000組參數帶入訓練好的BP神經網絡中，得到10 000個Z值并進行統計，如圖3所

示。可以看出，Z值符合正態分布，通過式（10）計算可靠性［5］，得到可靠性指標[β]為6.1，遠大于規范值一類破壞Ⅲ級規范值2.7。同理，構造擋土墻抗傾安全穩定計算得到可靠性指標[β]為7.5，大于規范值2.7。可見新型裝配式擋土墻有較高的安全富余，該擋土墻有優化空間。

[β=μzσz] （10）

2.2 參數敏感性分析

采用Sobol指數法分析因素敏感性，包括土體容重、墻中回填料容重、填土內摩擦角及土墻摩擦角。假設函數f（x）在定義域可積，變量x服從［0，1］區間均勻分布，則f（x）見式（11）、式（12）。

[f（x）=f0+nj=1 n i1<…<ijfi1…ijxi，…，xij] （11）

[f（x）=f0+ifixi+i<jfijxi，xj+…+i<jf1，2，…，nx1，x2，…，xn] （12）

式中：[1?i1<…<ij?n （1?j?n）]。

設f（x）滿足前置條件[01fi1…ijxi，…，xijdxk=0]，[k=i1，…，ij]，可將函數f（x）的總方差分解為式（13）。

[D=iDi+i<jDij+…+D1，2，…，n] （13）

式中：D為f（x）總體方差；[Di]為第i個參數的方差；[Dij]為第i、j個參數相互作用的方差；[D1，2，…，n]為n個參數共同作用下所產生的方差。

若各參數間作用敏感系數滿足式（14），則敏感系數的計算見式（15）至式（17）。

[iDiD+i<jDijD+…+D1，2，…，nD=1] （14）

[SCi=Di/D] （15）

[SCij=Dij/D] （16）

[SCTi=1-D～i/D] （17）

式中：變量xi的敏感系數用SCi表示；變量 xi和xj相互作用敏感系數用SCij表示；考慮變量xi和其他相關參數共同作用敏感系數用SCTi表示；其他參數產生的方差用D～i表示。

通過Sobol指數法計算輸入參數或輸入參數集合對輸出方差的貢獻，以確定參數在模型中具有的影響。填土內摩擦角Sobol指數為0.65，明顯高于土墻摩擦角Sobol指數0.17，土體容重和墻中回填料容重Sobol指數為3Ghc53B8pWNy7W5Y7c97Cg==0.11和0.07。綜上所述，對新型擋土墻穩定性影響強弱排序為填土內摩擦角>土墻摩擦角>土體容重>墻中回填料容重。

3 結論

①BP神經網絡代理模型能夠較好地替代新型擋土墻穩定性計算過程，能夠有效減少抗滑穩定計算、抗傾覆計算的計算次數，提高了新型擋土墻穩定性分析的計算效率，可通過較少的計算消耗獲得令人滿意的計算效率。

②研究的新型裝配式擋土墻的抗滑穩定、抗傾安全穩定可靠性指標分別為6.1和7.5，具有較高的安全富余，該擋土墻還有進一步優化設計的空間，傳統確定性方法估計擋土墻安全性偏保守。

③參數敏感性強弱排序為填土內摩擦角>土墻摩擦角>土體容重>墻中回填料容重，對填土內摩擦角度的準確測定估計是評價新型裝配式擋土墻穩定性的前提，在擋土墻設計過程中應重視。

參考文獻：

［1］吳國印，汪魁，易朋瑩，等.新型裝配式擋土墻穩定性影響因素敏感度分析［J］.重慶交通大學學報（自然科學版）， 2021， 40（9）： 92-100.

［2］劉云龍，張道兵，張標，等.基于孔隙水效應的多失效模式下擋土墻可靠性分析［J］. 湖南科技大學學報（自然科學版）， 2022， 37（1）： 1-9.

［3］趙明華，蔣沖，曹文貴.基于區間理論的擋土墻穩定性非概率可靠性分析［J］.巖土工程學報， 2008（4）： 467-472.

［4］鮑偉，任超.基于GWO-BP神經網絡的電池SOC預測方法研究［J］.計算機應用與軟件， 2022， 39（9）： 65-71.

［5］ZHENG Z， LI Y， WEN L， et al. Reliability analysis of an embankment dam slope based on an ellipsoid model and PSO-ELM［J］. Structures， 2023， 55： 2419-2432.