偶然性載荷作用下的橋式起重機(jī)擺角模型研究

摘"要：對(duì)起重機(jī)建立準(zhǔn)確的數(shù)學(xué)模型是研究其防搖擺控制策略的基礎(chǔ)。構(gòu)建在偶然載荷作用下橋式起重機(jī)搖擺數(shù)學(xué)模型，分析橋式起重機(jī)一個(gè)作業(yè)循環(huán)以及大小車(chē)運(yùn)行時(shí)的受力情況，在充分考慮偶然載荷作用下構(gòu)建橋式起重機(jī)工作過(guò)程中的三維動(dòng)力學(xué)數(shù)學(xué)模型。通過(guò)在驅(qū)動(dòng)力及風(fēng)載作用下對(duì)模型的仿真分析，研究橋式起重機(jī)的擺角變化規(guī)律。橋式起重機(jī)在偶然載荷作用下的擺角模型及其變化規(guī)律可為后續(xù)橋式起重機(jī)的防搖擺控制提供理論基礎(chǔ)，保證橋式起重機(jī)在偶然性載荷作用下工作安全可靠。

關(guān)鍵詞：橋式起重機(jī)；防搖擺；擺角模型；偶然載荷

中圖分類(lèi)號(hào)：TH215""文獻(xiàn)標(biāo)志碼：A""文章編號(hào)：1671-5276（2024）02-0116-04

Research on Bridge Crane Rocking Model under Accidental Loads

YU Zhen1，2， REN Haohao1，2， YU Jin1，2， WANG Liling3

（1. Key Laboratory of Metallurgical Equipment and Control Technology of Ministry of Education，Wuhan University of Science and Technology，Wuhan 430081， China; 2. Hubei Key

Laboratory of Mechanical Transmission and Manufacturing Engineering，Wuhan University of Science and Technology，

Wuhan 430081，China; 3. Wuhan Special Equipment Supervision and Inspection Institute，Wuhan 430014，China）

Abstract：Establishment of an accurate mathematical crane model is the basis for study of its anti-sway control strategy. This paper constructs a mathematical model for the sway of an overhead crane under accidental loads， analyzes the stress situation of the bridge crane during a working cycle and the operation of large and small vehicles， and builds a three-dimensional dynamic mathematical model during the operation of the bridge crane under the full consideration of accidental loads. The simulation analysis of the model under the action of driving force and wind load is conducted， and the change law of the swing angle of the bridge crane is studied. The swing angle model of bridge crane under accidental load and its variation law provide a theoretical basis for the anti-sway control of subsequent bridge cranes and guarantee the safety and reliability of the bridge cranes underthe action of accidental loads.

Keywords：bridge cranes；anti-sway；rocking model；accidental load

0"引言

作為裝備制造業(yè)領(lǐng)域的特種設(shè)備，橋式起重機(jī)在重要工礦企業(yè)中擔(dān)負(fù)著重要作用。橋式起重機(jī)在工作過(guò)程中的搖擺影響其工作安全性，工作過(guò)程中的各種偶然加劇了其搖擺的不確定性，因此需要充分研究橋式起重機(jī)在偶然載荷作用下的搖擺模型并制定防搖擺控制策略，保證橋式起重機(jī)的安全運(yùn)行。

本文根據(jù)起重機(jī)實(shí)際作業(yè)工況進(jìn)行載荷分析并建立大小車(chē)在負(fù)載作用下的運(yùn)動(dòng)過(guò)程動(dòng)力學(xué)微分方程，充分考慮風(fēng)擾對(duì)擺角的影響，構(gòu)建精確的搖擺數(shù)學(xué)模型并進(jìn)行仿真分析。

1"典型工況下橋式起重機(jī)載荷分析

橋式起重機(jī)由橋架結(jié)構(gòu)、運(yùn)行機(jī)構(gòu)、起升機(jī)構(gòu)、電氣裝置4部分組成。一般情況下，典型工況下工作流程為：1）負(fù)載起升過(guò)程；2）通過(guò)大車(chē)和小車(chē)的驅(qū)動(dòng)將吊重搬運(yùn)至目標(biāo)位置前方或者上方；3）將吊重自目標(biāo)位置上方垂直落下，結(jié)束本次工作行程。

引起起重機(jī)工作過(guò)程中搖擺的原因主要有兩方面：一是起重機(jī)的大、小車(chē)運(yùn)行機(jī)構(gòu)和主、副起升機(jī)構(gòu)在工作過(guò)程中的加減速運(yùn)動(dòng)而引起的吊重?cái)[動(dòng)；二是在作業(yè)過(guò)程中的一些不確定因素引起的擺動(dòng)，包括起重機(jī)在作業(yè)過(guò)程中受到的風(fēng)載荷、操作人員的操作失誤、軌道高低差等。

1.1"橋式起重機(jī)取物起升階段載荷分析

一般來(lái)說(shuō)，起重機(jī)取物起升過(guò)程分為三個(gè)階段：第一階段，起升機(jī)構(gòu)啟動(dòng)瞬間，鋼絲繩由松弛到拉直，此時(shí)忽略鋼絲繩自身質(zhì)量的話，鋼絲繩不受力，等效起升重物質(zhì)量m2靜止不動(dòng)；第二階段，鋼絲繩由拉直到拉緊，此時(shí)鋼絲繩受力從0～m2g，起升鋼絲繩從不受力狀態(tài)到拉力逐漸增大，通過(guò)卷筒及其支撐構(gòu)件將力F2（t）作用在橋架上，間接造成橋架受到的作用力由0開(kāi)始逐漸增大；第三階段，吊重離開(kāi)地面并與結(jié)構(gòu)發(fā)生共振，鋼絲繩受力達(dá)到最大，起升機(jī)構(gòu)產(chǎn)生的動(dòng)載荷最大。由于滑輪組中各個(gè)滑輪所受阻力不均，使得吊重產(chǎn)生的拉力不能均衡分配到每段繩索上，導(dǎo)致繩索張力不統(tǒng)一，系統(tǒng)為弱阻尼系統(tǒng)，造成負(fù)載輕微擺動(dòng)。由于初始擺動(dòng)的存在，大小車(chē)的加速運(yùn)動(dòng)會(huì)使擺動(dòng)加劇。因此模型的最終結(jié)果應(yīng)包括這部分振動(dòng)擺角［1］。

1.2"橋式起重機(jī)大（小）車(chē)加速階段載荷

起升機(jī)構(gòu)起升負(fù)載后，在水平運(yùn)動(dòng)過(guò)程中，起重機(jī)及其車(chē)輪等結(jié)構(gòu)受到水平慣性載荷、摩擦載荷和水平偏斜載荷作用。

1）移動(dòng)質(zhì)量水平慣性Fh

大車(chē)移動(dòng)的水平慣性是起重機(jī)自身質(zhì)量和負(fù)載在大車(chē)運(yùn)行機(jī)構(gòu)啟動(dòng)或者制動(dòng)時(shí)產(chǎn)生的沿軌道方向的水平慣性力，包括整機(jī)慣性力Fh2、帶載小車(chē)慣性力Fh1。

Fh=Fh2+Fh1（1）

2）軌道給車(chē)輪的滾動(dòng)摩擦以及起重機(jī)轉(zhuǎn)動(dòng)機(jī)構(gòu)的結(jié)構(gòu)阻力，構(gòu)成了其總運(yùn)行阻力［2］Fw：

Fw=∑Fmi·cd+2fD（2）

式中：c為轉(zhuǎn)動(dòng)機(jī)構(gòu)軸承摩擦因數(shù)；d為大車(chē)車(chē)輪輪軸樞直徑；D為大車(chē)車(chē)輪踏面直徑；f為滾動(dòng)摩擦因數(shù)；∑Fmi為車(chē)輪輪壓。

3）起重機(jī)偏斜移動(dòng)時(shí)水平側(cè)向力

起重機(jī)在運(yùn)行過(guò)程中由于軌道、車(chē)輪等在制造與安裝時(shí)誤差的存在、大小車(chē)軌道上表面不平和兩側(cè)驅(qū)動(dòng)電機(jī)的轉(zhuǎn)速或走輪直徑差異等因素的影響，車(chē)輪輪緣與軌道側(cè)面摩擦?xí)a(chǎn)生水平側(cè)向推力Fs，此時(shí)還會(huì)產(chǎn)生附加阻力Fz，從而導(dǎo)致負(fù)載產(chǎn)生斷斷續(xù)續(xù)的擺動(dòng)［3］，其求解經(jīng)驗(yàn)公式為

Fs=12λ∑Fmimax（3）

Fz=ζ·Fs（4）

式中：ζ為附加摩擦阻力系數(shù)；Fmimax為起重機(jī)受偏斜側(cè)向力一側(cè)車(chē)輪的最大總輪壓；λ為偏斜側(cè)向力系數(shù)。

4）風(fēng)載Fdy

起重機(jī)在室外作業(yè)時(shí)會(huì)受到風(fēng)載，風(fēng)載與風(fēng)壓和起重機(jī)的迎風(fēng)面積有關(guān)，因此在構(gòu)建起重機(jī)運(yùn)動(dòng)過(guò)程中的搖擺模型時(shí)，根據(jù)起重機(jī)的作業(yè)環(huán)境，需考慮因風(fēng)載作用而產(chǎn)生的負(fù)載偏擺影響［4］。

Fdy=S×Cf×P（5）

式中：P為計(jì)算風(fēng)壓；S為迎風(fēng)面積；Cf為吊重在受風(fēng)方向上的體形系數(shù)。

2"橋式起重機(jī)工作過(guò)程中的擺角模型構(gòu)建

2.1"橋式起重機(jī)

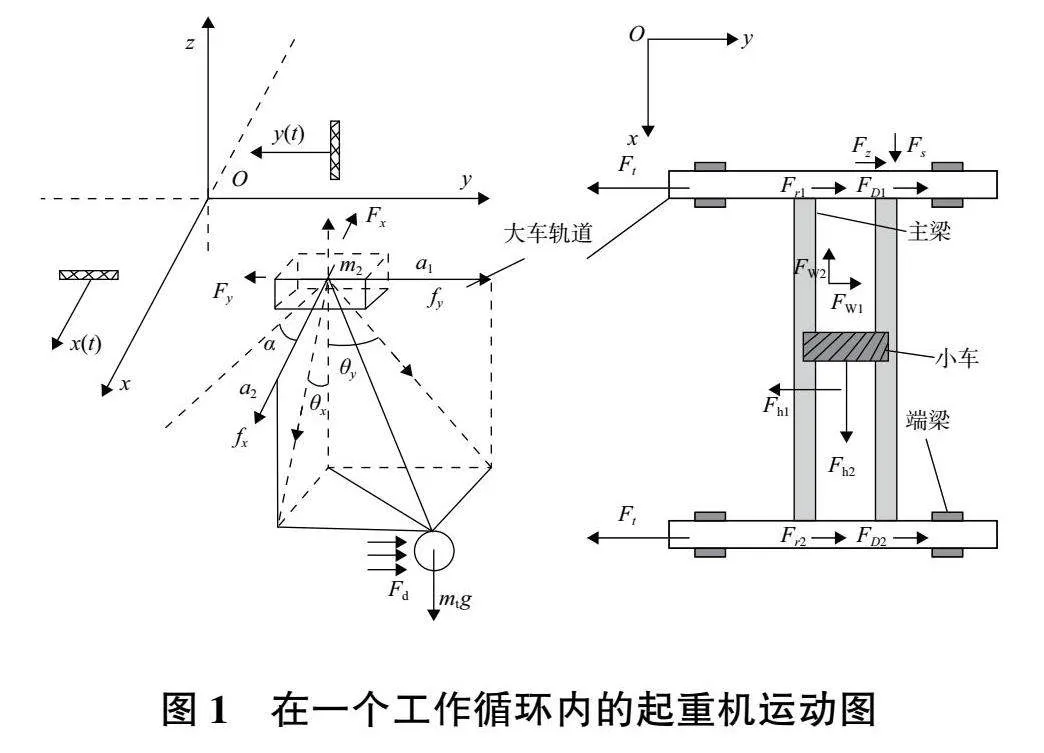
圖1為起重機(jī)大車(chē)運(yùn)行時(shí)在水平載荷作用下的負(fù)載載荷圖。當(dāng)起重機(jī)工作時(shí)，重物會(huì)通過(guò)繩索繞小車(chē)懸掛點(diǎn)進(jìn)行擺動(dòng)，擺角為θ，對(duì)擺角θ沿起重機(jī)前進(jìn)方向與重物在橋梁上面橫向的移動(dòng)方向進(jìn)行分解，得到θx與θy。Fx和Fy分別是驅(qū)動(dòng)大小車(chē)運(yùn)動(dòng)的驅(qū)動(dòng)力；fx、fy分別為大小車(chē)受到的摩擦阻力；a1、a2分別是大小車(chē)沿運(yùn)行方向的加速度；y（t）和x（t）表示對(duì)應(yīng)的x與y方向上的移動(dòng)位移；mt為負(fù)載質(zhì)量，m1和m2分別為小車(chē)和大車(chē)橋架結(jié)構(gòu)（包括走臺(tái)、主梁、端梁、小車(chē)等結(jié)構(gòu)）等效質(zhì)量。因軌道存在高低差，兩條軌道上表面不在同一平面，大車(chē)車(chē)身與水平面呈一夾角α。

2.2"橋式起重機(jī)工作過(guò)程中存在偶然載荷時(shí)y向擺角數(shù)學(xué)模型構(gòu)建

1）吊重起升階段產(chǎn)生的初始擺角如圖2所示。

橋式起重機(jī)在工作過(guò)程中，其鋼絲繩是一個(gè)彈性體，當(dāng)?shù)踔嘏c鋼絲繩保持靜止時(shí)，鋼絲繩受到的合拉力為負(fù)載重力Q，設(shè)Δl1和Δl2分別為左右兩根鋼絲繩在拉力載荷作用下產(chǎn)生的彈性伸長(zhǎng)量（單位為mm）。由虎克定律可知：每根鋼絲繩承擔(dān)的載荷值分別為Δl1×k，Δl2×k（k為鋼絲繩的剛度系數(shù)［5］）。設(shè)穿過(guò)該滑輪組有n組鋼絲繩，對(duì)吊重進(jìn)行受力分析，則

（ihFjmax+∑ni=1Δlik）cosβ=Q=mtg（6）

Fjmax=Qihηh，k=EAl（7）

式中：Fjmax為繞入卷筒的鋼絲繩最大靜拉力（為便于計(jì)算，假設(shè)每根鋼絲承受的拉力相同，且都為最大張力）；Q為起升載荷及吊具質(zhì)量之和；ih為滑輪組倍率；ηh為滑輪組效率（查手冊(cè)可得）；E為鋼絲繩等效彈性模量；A為鋼絲繩橫截面積；l為鋼絲繩的總長(zhǎng)度，由此可得起升鋼絲繩初始擺角為

β=arccosQ（ihFjmax+∑ni=1Δlik）（8）

2）當(dāng)大車(chē)沿y方向運(yùn)動(dòng)且有風(fēng)載時(shí)，其載荷分析如圖3所示。

以大車(chē)位移方向（向左為正方向）為y向構(gòu)建坐標(biāo)系，得到大車(chē)運(yùn)動(dòng)動(dòng)力學(xué)微分方程：

（m2+mt）y··=Fy－f－Fdy－Fz（9）

對(duì)于起吊重物為研究對(duì)象，進(jìn)行分析：

Flsinθ1y－Fdy=mty··（10）

式中θ1y為在大車(chē)運(yùn)動(dòng)過(guò)程中，起升重物與豎直方向的夾角。由式（9）、式（10）可解得：

θ1y=arcsinmt（Fy－fda－Fz－Fdy）（m2+mt）Fl+FdyFl（11）

式中大車(chē)車(chē)輪組與軌道之間的摩擦力fda可表示為

fda=（Flcosθ1y+m2）μ（12）

式中μ為大車(chē)車(chē)輪組與軌道之間的動(dòng)摩擦因數(shù)。

則式（11）計(jì)算可得：

θ1y=

arcsinmt（Fy－（Flcosθ1y+m2）μ－Fz－Fdy）（m2+mt）Fl+FdyFl

θ1y=arcsinmt（Fy－Flcosθ1yμ－m2μ－Fz－Fdy）（m2+mt）Fl+FdyFl（13）

根據(jù)起升重物在豎直方向載荷分析可知：

Flcosθ1y=mtgFl=mtgcosθ1y（14）

θ1y=arcsinmt（Fy－mtgμ－m2μ－Fz－Fdy）（m2+mt）+""Fdycosθ1ymtg（15）

將式（3）—式（5）代入式（15）得

θ1y=arctanmt（Fy－mtgμ－m2gμ－ζ×12λ∑Fmimax）（m2+mt）+S×Cf×P1mtg（16）

綜上可得y方向擺角為

θy=β+θ1y=arccosQ（ihFjmax+∑ni=1Δlik）+

arctanmt（Fy－mtgμ－m2gμ－ζ×12λ∑Fmimax）（m2+mt）+S×Cf×P1mtg

（17）

2.3"起重機(jī)在偶然載荷作用下時(shí)x方向擺角數(shù)學(xué)模型構(gòu)建

當(dāng)大車(chē)軌道存在高低差時(shí)，大車(chē)主梁與水平方向存在夾角α，考慮x向風(fēng)載時(shí)，小車(chē)受力分析如圖4所示。

由此得到小車(chē)運(yùn)動(dòng)過(guò)程的動(dòng)力學(xué)微分方程為

（m1+mt）x··=Fx－fxiao－Fdx－Flsinθx－m1gsinα（18）

式中：fxiao為小車(chē)車(chē)輪組與導(dǎo)軌之間的摩擦力；Fdx為x向風(fēng)載，則：

fxiao=（Flcosθx+m1gcosα）μ（19）

（m1+mt）x··=Fx－（Flcosθx+m1gcosα）μ－Fdx－

Flsinθx－m1gsinα

x··=Fx－（Flcosθx+m1gcosα）μ－Flsinθx－Fdx－m1gsinαm1+mt（20）

以起吊重物為研究對(duì)象進(jìn)行分析：

Flcosπ2－（θx－α）－Fdx=mtx··=

mtFx－（Flcosθx+m1gcosα）μ－Fdx－Flsinθx－m1gsinαm1+mt（21）

一般情況下，h在0～10mm范圍內(nèi)，因此sinα≈0，cosα≈1，式（21）可整理為

Flsinθx－Fdx=mtFx－（Flcosθx+m1g）μ－Fdx－Flsinθxm1+mt（22）

根據(jù)起吊重物在豎直方向載荷分析可知：

Flcosθx=mtgFl=mtgcosθx

mtgtanθx－Fdx=

mtFx－（mtg+m1g）μ-Fdx－mtgtanθxm1+mt

tanθx=mtFx－（mtg+m1g）μ－Fdxm1+mt+Fdx×（m1+mt）（m1+mt+1）mtg（23）

起重機(jī)在x方向的擺角分量為

θx=arctanmtFx－（mtg+m1g）μ－Fdxm1+mt+Fdx×（m1+mt）（m1+mt+1）mtg（24）

2.4"橋式起重機(jī)總擺角模型

由此可得，在偶然載荷作用下，橋式起重機(jī)綜合擺角模型為

θ=（θy）2+（θx）2

θ=arccosQ（ihFjmax+∑ni=1Δlik）+arctanmt（Fy-mtgμ-m2gμ-ζ×12λ∑Fmimax）（m2+mt）+S×Cf×P1mtg2+

arctanmtFx-（mtg+m1g）μ-Fdxm1+mt+Fdx×（m1+mt）（m1+mt+1）mtg2（25）

3"負(fù)載擺角影響因素分析

3.1"驅(qū)動(dòng)力大小對(duì)擺角的影響

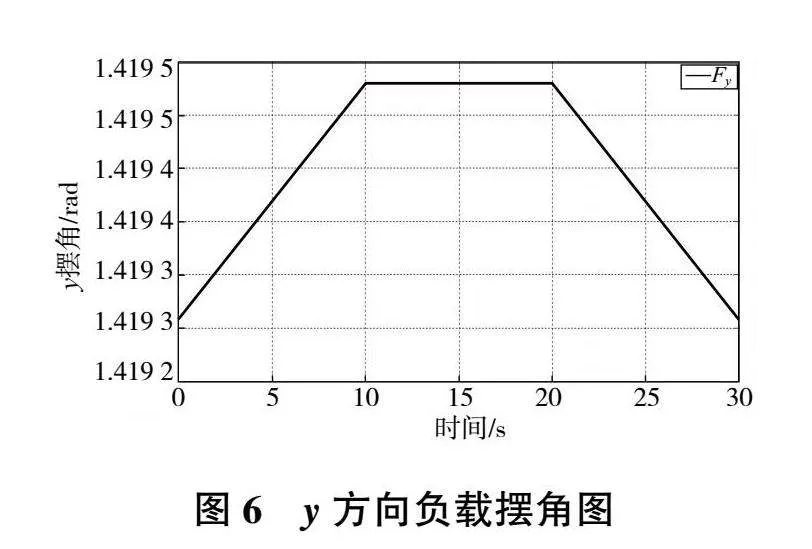
圖5為起重機(jī)在工作過(guò)程中的驅(qū)動(dòng)力作用波形：0～10s時(shí)，F(xiàn)y呈線性增加趨勢(shì)；10～20s驅(qū)動(dòng)力保持不變；20～30s驅(qū)動(dòng)力大小呈線性減少趨勢(shì)。通過(guò)該驅(qū)動(dòng)力作用曲線，對(duì)式（25）進(jìn)行分析，得到如圖6所示的同一驅(qū)動(dòng)力Fy在不同作用時(shí)間下的擺角-時(shí)間曲線，圖中各時(shí)間段分別表示起重機(jī)加速、勻速、減速過(guò)程。

3.2"風(fēng)載對(duì)擺角的影響

為研究風(fēng)載對(duì)擺角的影響，本實(shí)驗(yàn)在保持其他參數(shù)不變情況下，大小車(chē)驅(qū)動(dòng)力設(shè)為3 000N，對(duì)仿真模型模擬輸入分別為正、負(fù)300N的不同方向風(fēng)力，通過(guò)分析得出：正方向（順）風(fēng)載存在時(shí)擺角最大達(dá)到了1.419 6rad，負(fù)方向（逆）時(shí)最大達(dá)到了1.419 2rad。由此得知當(dāng)風(fēng)向與負(fù)載擺動(dòng)方向相同時(shí)擺角增大，相反時(shí)對(duì)負(fù)載擺動(dòng)有輕微抑制作用。

4"結(jié)語(yǔ)

本文在橋式起重機(jī)的一個(gè)工況下，根據(jù)起重機(jī)擺角在空間的狀態(tài)，將其分解為大、小車(chē)兩個(gè)移動(dòng)方向的分量并對(duì)分量進(jìn)行建模分析，考慮繩長(zhǎng)變化、大車(chē)雙軌夾角以及風(fēng)載等因素構(gòu)建了其擺角模型并仿真分析驅(qū)動(dòng)力、風(fēng)載對(duì)負(fù)載擺角的影響。研究結(jié)果表明：初始擺角不可忽略，起重機(jī)的加減速度會(huì)加大負(fù)載擺動(dòng)幅度，風(fēng)載的大小及方向?qū)Φ踔氐膿u擺產(chǎn)生影響，但是對(duì)幅度的絕對(duì)值變化影響不大。該研究結(jié)果可為以后起重機(jī)防搖實(shí)驗(yàn)提供理論基礎(chǔ)。

參考文獻(xiàn)：

［1］ 馬旭，王宗彥，劉巖松，等. 改進(jìn)子模型分析法對(duì)起重機(jī)主梁靜態(tài)特性影響研究［J］. 機(jī)械制造與自動(dòng)化，2020，49（06）：72-74.

［2］ 楊慶，計(jì)三有，姜爭(zhēng). 龍門(mén)起重機(jī)偏斜運(yùn)行分析及計(jì)算［J］. 起重運(yùn)輸機(jī)械，2020（22）：47-52.

［3］ GB/T 3811—2008起重機(jī)設(shè)計(jì)規(guī)范［S］.

［4］ 錢(qián)夏夷，殷晨波，馬峰. 船用門(mén)式起重機(jī)動(dòng)載荷的確定方法［J］. 機(jī)械制造與自動(dòng)化，2013，42（4）：88-91.

收稿日期：20220920