基于γ光子的葉片沉積物檢測系統的設計

摘"要：針對目前利用γ光子進行發動機葉片沉積物檢測需要的流程多，且沒有相應軟件平臺的問題，設計一個γ光子探測裝置控制與圖像處理系統軟件，包括控制探測器進行數據的采集模塊、檢測圖像處理模塊以及點云配準模塊等的設計。該系統基于Qt平臺，集成了VTK、ITK、PCL等C++類庫，并設計實現一種基于PCA-ICP的點云配準算法優化。經實驗測試表明：該配準算法能夠有效提高沉積物檢測的效率及精度，并且該系統設計能夠實現對探測裝置的控制并滿足對圖像的處理要求。

關鍵詞：γ光子；無損檢測；軟件設計；圖像處理，點云配準

中圖分類號：TB302.5""文獻標志碼：A""文章編號：1671-5276（2024）02-0035-05

Design of Engine Blade Sediment Detection System Based on γ Photon

GAO Chaoyu， YAO Min， CHEN Shuyi， WANG Ming

（College of Automation Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing 211106， China）

Abstract：Regarding the complex processes of engine blade detection by means of γ photon and lack of related software platform， this paper designs a γ photon detection device control and image processing system software， which includes the design of data acquisition module， detection image processing module and point cloud registration module controling the detector. Based on Qt platform， the system integrates VTK，ITK，PCL and other C++class libraries， and designs and implements a point cloud registration algorithm optimization based on PCA-ICP. The experiments show that the registration algorithm can effectively improve the efficiency and accuracy of sediment detection， and the system design can achieve the control of detection devices and meet the requirements of image processing.

Keywords：γ photons; non destructive testing; software design; image processing; point cloud registration

0"引言

利用γ光子發動機葉片沉積物檢測是一種新的檢測手段。將放射性核素與熔融態石蠟顆粒混合，通過風洞模擬沉積的動態過程，直至熔融態顆粒在發動機葉片上沉積。在外部通過γ光子探測裝置接收發射出的γ光子對，經過重建能夠得到葉片沉積物的三維圖像，之后對該圖像進行濾波、邊緣提取等處理，能夠獲得有效的沉積物檢測圖像。將處理后的圖像轉換成點云數據，與葉片模型點云數據進行配準，即可判斷沉積物在葉片的分布，達到檢測的目的。但是，由于目前還沒有能夠將上述處理過程集成在一起的軟件平臺，導致檢測過程較為繁瑣，需要在不同平臺上進行切換處理。因此，本文設計了一款γ光子探測及圖像處理系統軟件，并結合γ光子點云圖像的特點對其中點云配準模塊所用的配準算法進行了優化，將γ光子檢測所需的流程進行集成，為以后檢測的標準化提供解決方案。

1"系統總體設計

本文設計的系統基于Qt開發，Qt具有良好的封裝機制，其模塊化程度非常高。此外，Qt的信號槽機制非常高效實用，加上豐富的API，便于開發者理解，最重要的是它還支持2D/3D圖形渲染，支持OpenGL，因此廣泛用于軟件界面的開發設計。同時，更為重要的是，Qt采用C++編寫，使之后的圖像處理以及點云配準模塊均可調用C++的類庫，大大方便了軟件的開發過程［1-2］。

γ光子探測及圖像處理系統包含了以下幾個重要的模塊：探測器控制模塊、圖像處理模塊、點云配準模塊和圖像顯示模塊等。

1.1"探測器控制模塊

探測器控制模塊采用DMC1380運動控制卡來發送控制指令給步進電機來控制齒輪旋轉，從而將探測器送至指定的位置進行采集。該控制卡采用了專用運動控制卡，可以對多個步進電機進行點位運動控制，并且提供了一套簡單易用的、功能豐富的運動控制API函數庫，大大提高了開發的效率。控制指令通過CAN總線來傳輸，因為CAN總線的數據段長度最多為8個字節，8個字節不會占用總線時間過長，從而能夠保證通信的實時性。該模塊的工作原理如圖1所示。

該模塊主要實現以下的功能：顯示當前運動狀態，判斷裝置處于旋轉或者停止狀態；顯示旋轉的方向，判斷是否處于采集狀態或者回零狀態；顯示旋轉速度，判斷當前速度是否滿足設定要求；同時還可以顯示當次采集的采集進度，用來判定當前采集是否結束。

1.2"圖像處理模塊

因為利用γ光子對沉積物檢測得到的切片圖為DICOM格式。DICOM是一種標準的醫學圖像格式，所以圖像處理模塊利用了ITK庫對DICOM數據讀取和處理，包括濾波、讀取DICOM數值等基本處理。但是，ITK沒有顯示圖像的功能，因此將處理后的數據利用VTK進行顯示。VTK是一個可視化工具包，主要應用在三維計算機圖形、圖像處理以及可視化方向作為一個專業的可視化工具，它還具有強大的三維圖形功能，可以利用光線投射法進行三維體繪制，還能進行逼真的體、面、光源等渲染。上述這些特性，可以很好地將檢測結果呈現出來，實現數據的可視化。

1.3"點云配準模塊

由于γ光子檢測手段只能獲取到沉積物的三維圖像，無法得到沉積物在葉片上的準確分布。因此采用了將檢測得到的數據轉換成點云數據與發動機葉片的空腔點云進行配準的方式實現檢測的目的，以此來反映沉積物在葉片的分布情況，并對之后的葉形設計提供輔助作用。該模塊的任務就是將檢測到的序列切片圖轉換成點云數據，同時獲取葉片的點云數據。該模塊基于點云庫（point cloud library，PCL）來實現，PCL是目前比較流行的點云處理庫，用來實現點云濾波、配準等點云處理中常見的問題［3］。

1.4"圖像顯示模塊

本文設計的檢測系統有較多的可視化需求，包括對序列檢測切片圖的可視化、圖像處理過程的可視化、點云數據處理過程中的可視化。圖像顯示模塊考慮到Qt與VTK的結合，采用了VTK中可視化模塊［3］，集成到Qt界面，來滿足該檢測系統的可視化需求。

2"點云配準算法優化

由于γ光子檢測得到的數據是體數據，而體數據的數據量較大，會導致配準時間長，并且在γ光子成像過程中存在散射現象，導致在將圖像轉換為點云數據時存在大量的噪聲點。因此分別對γ光子檢測的體數據和內腔模型的點云數據進行降采樣處理并通過濾波減少檢測點云中存在的噪聲，針對經典PCA算法出現的主軸反轉情況［4-5］提出了改進的PCA算法，結合γ光子檢測點云的特點，利用列文伯格-馬夸爾特（levenberg-marquardt，LM）算法對迭代最近點（iterator closest points， ICP）算法進行了優化。

2.1"基于主軸校正的PCA算法

1）首先，將點云坐標記為矩陣P，矩陣P的每一行分別記錄了點云中一個點空間坐標的x、y、z坐標值，第i個點的坐標記為pi（pxi，pyi，pzi）：

P=px1py1pz1px2py2pz2pxnpynpzn（1）

2）遍歷點云中所有的點，假設該點云中共有n個點，計算點云的中心空間坐標，記為O：

O=1n∑ni=1pxi，∑ni=1pyi，∑ni=1pzi（2）

3）采用協方差矩陣來計算不同維度之間的協方差，協方差矩陣可以通過式（2）進行構造：

C=1n∑ni=1［（pi-O）（pi-O）T］（3）

4）利用奇異值分解的方法來計算協方差矩陣C的特征值和特征向量，奇異值分解的形式為

C=UΛUT（4）

5）分別計算源點云和目標點云的主軸方向，利用源點云和目標點云的主軸方向矩陣計算源點云變換到目標點云的旋轉矩陣R：

R=UtUs-1（5）

6）在得到旋轉矩陣R以后，平移矩陣可以通過式（5）求取：

T=OT-ROS（6）

式中：OT表示目標點云的中心坐標；OS表示源點云的中心坐標。

那么最終的變換矩陣即由旋轉矩陣R和平移矩陣T構成：

Trans=R0T1（7）

由于PCA算法計算得到的主軸方向采用向量的形式表示，因此在計算主軸之后可能出現主軸反向的問題，故本文提出一種改進的算法用于解決主軸反向的問題。在得到變換矩陣之后，分別構造x、y、z軸旋轉矩陣：

V=d1000d2000d3（8）

式中d1、d2、d3的取值為1或者-1，共有8種不同的組合，對應將x、y、z軸3個方向進行反轉。分別計算8種情況下的兩組點云的配準誤差δi（i=1，2，3，…，8），取誤差最小的δk對應的Vk。用Vk校正由式（5）計算得到的旋轉矩陣R：

R′=R×Vk（9）

式中R′是經過主軸校正得到的旋轉矩陣。

2.2"改進的ICP算法

ICP算法是點云配準領域最經典的配準算法。該算法的核心是構造一個目標函數，通過多次迭代來使得目標函數最小化。利用粗配準的變換矩陣作為算法的初值進行迭代計算［6］。算法的目的就是尋找最優的旋轉矩陣和平移矩陣使得目標誤差函數E（R，t）的值最小。

求解最優的旋轉矩陣和平移矩陣，按照如下步驟進行求解。

1）計算源點云P和目標點云Q的重心，分別記為Wp（xwp，ywp，zwp）和Wq（xwq，ywq，zwq），可以通過式（10）和式（11）分別計算Wp和Wq：

Wp=1m∑mi=1px，∑mi=1py，∑mi=1pz（10）

Wq=1n∑ni=1qx，∑ni=1qy，∑ni=1qz（11）

2）協方差矩陣計算如下：

C=1k∑ki=1［piqiT］-WpWqT（12）

3）利用協方差矩陣構造對稱矩陣Sym，求解對稱矩陣的最大特征值，對應的特征向量即為最優的旋轉向量，對稱矩陣Sym為

Sym（C）=tr（C）ΔTΔC+CT-tr（C）I3（13）

4）采用四元素法來計算最優變換矩陣，記最優旋轉向量rot=［q0q1q2q3］T，q0、q1、q2、q3滿足q0≥0，并且q02+q12+q22+q32=1，采用四元素法計算最優旋轉矩陣R，得到最優旋轉矩陣R后，求解最優的平移矩陣t：

t=Wp-RWq（14）

將R和t帶入目標函數就可以計算得到兩片點云對應k個點的歐式平均距離e。當e小于等于設定的閾值時，則當前的最優旋轉矩陣R和最優平移矩陣t為全局最優的旋轉矩陣和平移矩陣。如果當前計算的e大于設定的閾值那么就需要重新求解步驟1）到步驟4），得到新的R和t，直到e小于等于設定的閾值。

由于γ光子檢測點云屬于無序點云并且點云數據量巨大，在搜索對應點時會耗費大量的時間，在多次迭代搜索后，時間復雜度也會隨之提高，同時經典的ICP算法在部分情況下可能會產生局部最優解的問題。針對此問題，本文通過引入LM模型來求解最優的變換矩陣。

高斯-牛頓法是求解非線性問題常用的方法，在實際使用中，高斯-牛頓法要求正規方程中的海塞矩陣H為正定矩陣，但是可能會遇到海塞矩陣H為奇異矩陣的情形。因此，高斯-牛頓法可能存在不收斂的情況，不能適應所有的最優化求解。

LM算法在高斯-牛頓法中加入了一個正定的對角矩陣，那么增量變化為

Δx=-（J（x）TJ（x）+λI）-1J（x）Te（x）（15）

式中：I為單位矩陣；λ為一個正實數。當λ=0時，LM算法和高斯-牛頓法相同，當λ很大時，LM算法就變成了梯度下降法。因此，λ用于控制優化算法前進的步長，在前期將λ設置為較大的值，使得x通過梯度下降法快速收斂到極值點附近；當x收斂到極值點附近后，將λ減小到0附近，減少收斂的步長，使其達到穩定收斂的效果。在每次迭代的時候，除了要更新誤差函數e（x）在第k次迭代值xk和在該處的一階偏導數值以外，還要更新λ的值，用于調節收斂步長。λ選取的策略為：

λ的初始值為max（aij），aij為HG-N矩陣對角線元素，在迭代過程中定義兩個變量μ和ν，其中ν的初始值設置為2。

μ=F（xk+1）-F（xk）ψ（xk+1-xk）-ψ（0）（16）

式中：ψ（x）為F（x）的線性近似函數；μ代表了目標函數與近似函數變化量的差異。線性近似函數總是大于0，因此，如果μ＜0則說明前進的方向是正確的，目標函數F（x）變小，那么下一次迭代中的λ則更新為

λ=λ·max13，1-（2μ-1）3（17）

如果求得μgt;0則說明前進方向錯誤，就通過ν調整μ：

μ′=μ·ν，v′=2·ν（18）

當x的增量太小時，則可以認為目標函數已經收斂到極值點附近了，可以停止迭代，判斷條件為

xk+1-xk＜ε（xk+ε）（19）

式中ε為自定義的比較小的一個正值。

本文提出的改進ICP算法如下。

1）對源點云和目標點云進行數據重組，分別構建源點云和目標點云的kd-tree結構。

2）將ICP算法的目標函數記為誤差函數：

e（R，t）=1k∑ki=1qi-（R+t）2（20）

由誤差函數計算雅可比矩陣J。根據λ的選取策略修改λ，并計算誤差，當誤差小于設定的閾值時，停止迭代；當誤差大于設定的閾值時，繼續更新λ，直至誤差小于設定的閾值，完成配準計算。

3"系統測試與實驗結果

3.1"系統整體測試

如圖2所示，在控制探測裝置進行旋轉采集時，可以在控制界面顯示當前的旋轉方向、轉速、當前角度以及當前探測裝置的狀態等信息，同時，在探測過程中一旦出現錯誤還可以人工停止采集；在采集結束之后，可以控制探測裝置順時針旋轉至原始位置，準備下一次的采集操作。

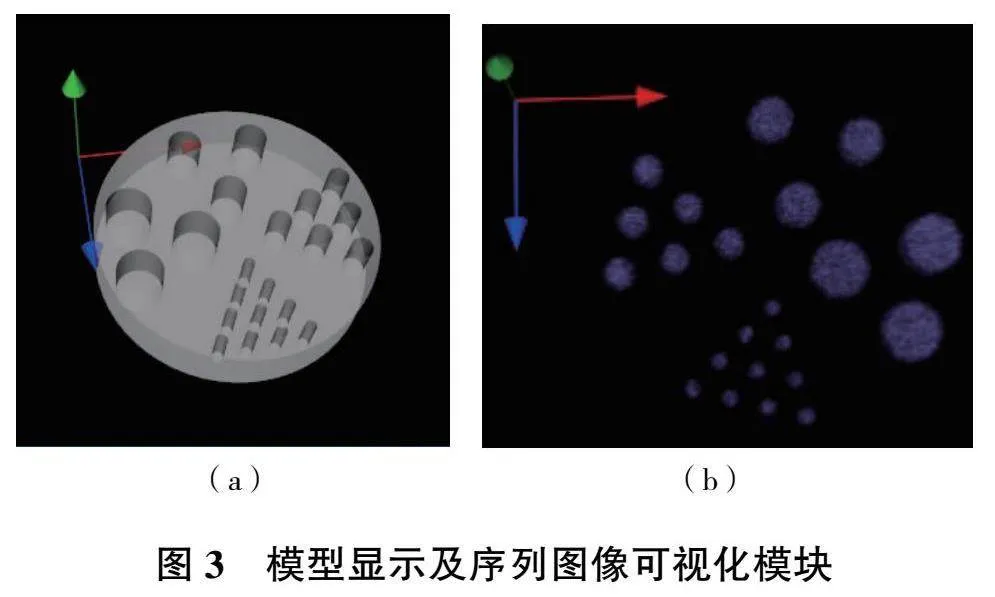
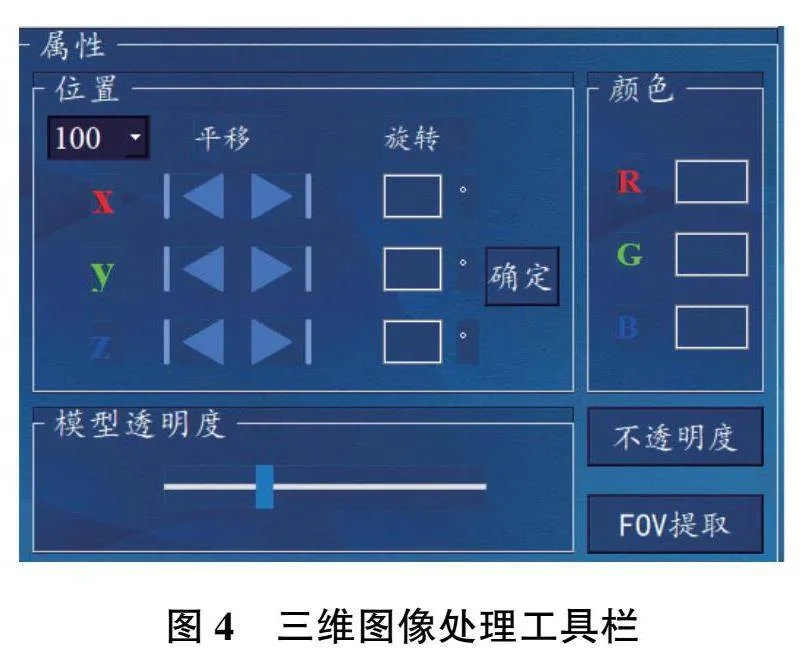
圖3和圖4分別展示了對檢測模型和序列圖像的三維顯示以及圖像處理的部分功能。

3.2"點云配準算法對比

為驗證檢測效果，現場實驗使用的探測器為Trans-PET Discoverist 180，其部分參數如表1所示。

Trans-PET Discoverist 180探測器如圖5所示。

利用風洞模擬顆粒在發動機葉片沉積的過程，通過γ光子成像算法獲得沉積物圖像，并將其轉換為點云數據與葉片進行配準。為驗證本文提出的改進PCA-ICP算法在γ光子沉積物檢測中的效果，利用經典的PCA-ICP算法和改進的PCA-ICP算法分別為葉片沉積物及葉片進行配準。兩種配準算法的結果如圖6所示。

圖6中綠色表示沉積物的γ光子點云圖像，紅色表示發動機葉片的理論模型，藍色表示配準后沉積物在葉片的分布（本刊為黑白印刷，有疑問可向作者咨詢）。圖6（a）為傳統的PCA-ICP配準算法的結果，根據結果可以發現，配準出現錯誤，存在主軸反轉，并且存在一定的角度偏差，圖6（b）為改進后的PCA-ICP算法配準結果，利用改進的PCA-ICP算法作為粗配準結果，修正了主軸反轉，經過精確配準之后得到了正確的配準結果。

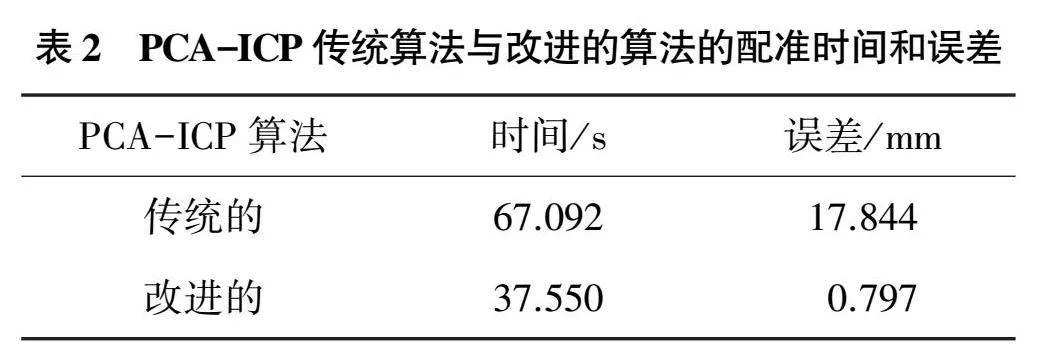
表2比較了兩種配準算法的耗時和誤差，可以看到在時間上本文提出的改進算法占有優勢，均小于傳統的PCA-ICP算法所消耗的時間；同時，改進的算法配準誤差均小于傳統PCA-ICP算法得到的誤差。與圖6中展示的結果一致，由此證明在γ光子葉片沉積物檢測中，本文提出的改進的PCA-ICP算法是有效的，并且效果優于傳統的PCA-ICP算法。

在實際檢測環境中，γ光子檢測圖像中會產生較多的噪點，并且由于γ光子檢測圖像得到的檢測數據是體數據，數據量大，將其中轉換為點云數據之后，常規的配準算法配準時間較長，為進一步驗證本文提出的改進的PCA-ICP算法在葉片沉積物檢測中的優越性和穩定性，延長了顆粒沉積實驗的實驗時間，使得更多的顆粒沉積在葉片上，并且在得到的數據中增加噪點來驗證本文提出的算法的穩定性。

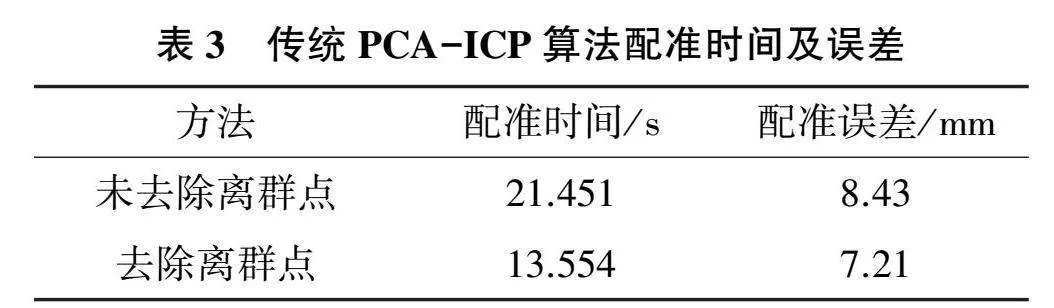
實驗獲得的沉積物點云數據為62 896個。將該點云作為源點云，葉片的點云數據為18 648個。該點云數據作為目標點云，通過對源點云增加離群點的方法，將源點云數據擴充到76 222個。傳統的PCA-ICP算法的配準時間及配準誤差如表3所示。

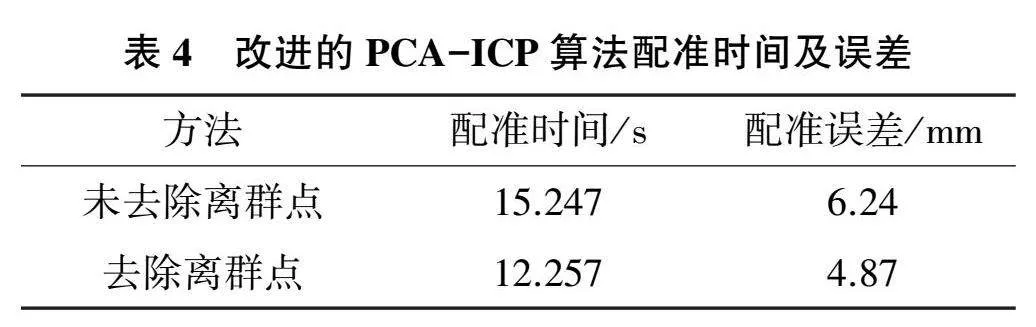
改進的PCA-ICP算法的配準時間及配準誤差如表4所示。

增加的離群點數量約占整體點云的17.51%，由于離群點的存在，在計算對應點時會增大誤差，并且增加配準時間，對于改進的PCA-ICP算法來說，去除離群點和未去除離群點的配準時間相差并沒有傳統PCA-ICP算法的配準時間相差大，此外，在有離群點的情況下，改進后的算法配準時間也較短。由此可以看出，改進的PCA-ICP算法的精度與去除離群點情況下的配準精度相當，該算法具有較好的穩定性，優于傳統的PCA-ICP算法，并且改進后的算法在數據量較大的情況下也有較好的表現。

4"結語

本文設計了一款基于工業γ光子的發動機葉片沉積物探測及圖像處理系統軟件，基于Qt平臺，加入了VTK、ITK、PCL 3個C++類庫，分別用來實現圖像的顯示、DICOM數據的讀取與處理以及對點云數據的處理，并通過對點云配準算法進行改進，提高了配準精度和效率，經過多次實驗測試，該系統達到了設計目標。

參考文獻：

［1］ 李科，岳林，惠子南，等. 基于Qt跨平臺的車載人機界面設計［J］. 鐵道標準設計，2017，61（9）：128-132.

［2］ 陳明，沈鉞. 基于Qt開發的水下航行器監控系統［J］. 計算機產品與流通，2019（11）：144.

［3］ 曲濱鵬，魏曉潔，繆佳，等. 圖像分割技術在醫學圖像處理中的應用實踐［J］. 科技創新與應用，2021（16）：178-180.

［4］ 李澤宇，何萍，朱立峰. 一種基于PCA的醫學圖像特征提取與配準算法研究［J］. 中國數字醫學，2020，15（7）：98-101.

［5］ RUSU R B，MARTON Z C，BLODOW N，et al. Towards 3D Point cloud based object maps for household environments［J］. Robotics and Autonomous Systems，2008，56（11）：927-941.

［6］ 邢宏文，劉思仁，邱磊，等. 基于點云數據的零件數字化檢測技術研究［J］. 機械制造與自動化，2020，49（6）：217-219.

收稿日期：20221019