淺談三角形的外心和內心

三角形的外心和內心與軸對稱圖形、三角形、圓等都有一定的知識聯系，加上近年來比較熱點的“用無刻度直尺畫圖”與之也聯系甚密，成為初中數學考試中的高頻考點，引起了數學教師的高度重視。在初中階段，教學三角形的外心和內心時，必須抓住它們的本質和來源，注重靈活運用其他與之相關的數學知識和技能，采用變式的手段，加深學生對這兩個概念的理解。

一、確定三角形的外心和內心

依據三角形的外心是三角形三邊垂直平分線的交點，三角形的內心是三角形三個內角平分線的交點，可以確定三角形的外心和內心。

（一）作圖確定三角形的外心和內心

1.外心

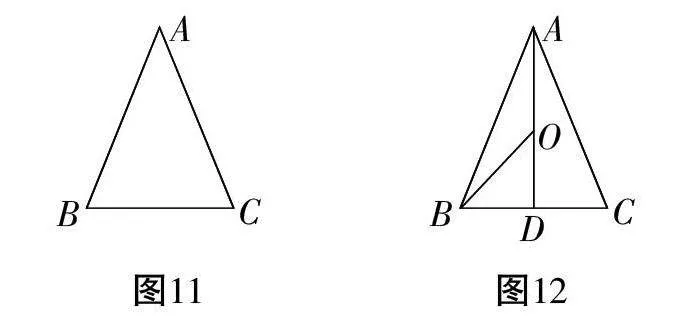
作三角形兩邊的垂直平分線，其交點就是三角形的外心。如圖1所示，在△ABC中，分別作BC、AB的垂直平分線PQ、MN，PQ與MN交于點O，則點O就是△ABC的外心。

2.內心

作三角形兩個內角的平分線，其交點就是三角形的內心。如圖2所示，在△ABC中，分別作∠ABC、∠ACB的平分線BD和CE，BD與CE交于點I。則點I就是△ABC的內心。（二）借助網格圖找三角形的外心和內心

1.外心

（1）利用兩邊的垂直平分線的原理作出外心。

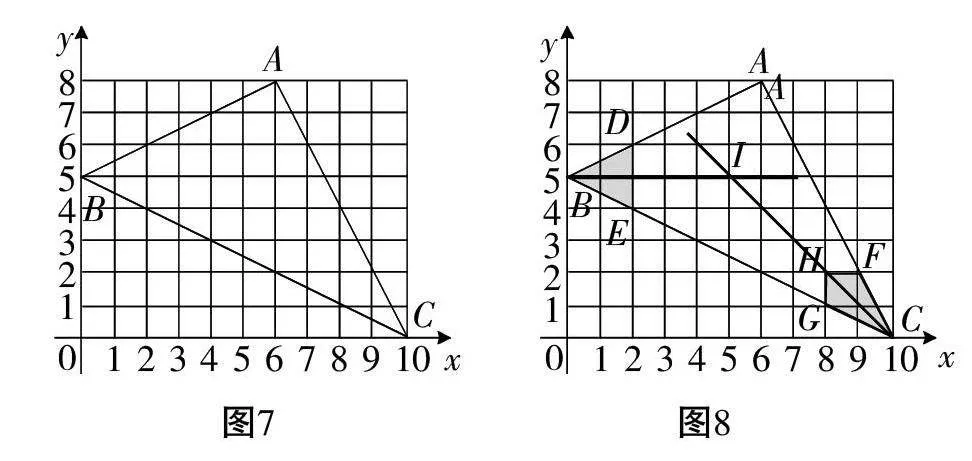
例1.如圖3所示，△ABC的頂點坐標分別為A（0，2）、B（1，3）、C（3，3），僅用無刻度的直尺作出外心的位置。外心的坐標為_______。

分析：BC的垂直平分線就是直線x=2;A（0，2）、B（1、3）兩點恰好在一個網格正方形的對角上，線段AB的垂直平分線為直線y=-x+3。用無刻度的直尺畫出來，兩條直線交于點O，則0點就是外心，其坐標為（2，1），如圖4所示。

（2）利用外心到三角形三個頂點的距離相等作出外心。

例2.如圖5所示，△ABC的頂點坐標分別為A（1，1）、B（7，3）、C（3，5）。……