基于結構化視角探索知識本質

[摘 要] 教師所秉承的教學理念，對課堂來說起到決定性作用，一個教師若將教學的側重點放在問題的解法探索上，就很難真正揭露知識本質，而將教學的側重點放在幫助學生構建知識的結構化體系上，則可起到事半功倍的效果. 文章以“一次函數的圖象”的復習教學為例，從現狀分析、教學分析、教學設計及教學思考等方面展開探索與研究.

[關鍵詞] 結構化;知識本質;復習;一次函數

科學本為統一體，將它劃分成各門學科并非由知識本質所決定，而是迫于人類認知的局限與實際需要，從本質上來說，數學、物理、化學、人類學、社會學……之間存在很強的聯系，眾多學科中，數學的內在統一性更為明顯. 從結構化的視角探尋數學知識本質，一方面能讓學生從簡約的維度完善知識結構，另一方面能讓學生增強對知識檢索與記憶功能，為知識的遷移與應用夯實基礎. 本文以“一次函數的圖象”的復習教學為例，探討如何基于結構化視角探索知識本質.

現狀分析

1. 知識的“間斷性”與“結構化”間的矛盾

雖然新課改的不斷深入推進有效提高了數學課堂教學的效率，然而，受課時的局限性影響，教學內容分散的問題一直存在，這種知識的“間斷性”與新課標所倡導的“結構化”理念形成了沖突. 為了處理好這一矛盾，教師可結合學情與教情，從結構化的角度設計課堂教學方案，引導學生在自主合作與深入探索中發現知識本質，構建完整的知識體系，獲得結構化的思維.

2. 課堂過度開放致使教學主線不明朗

課堂中，有些教師雖然具備了基于結構化視角揭露知識本質的意識，但課堂上因為過度強調“開放”導致教學主線不明確，學生只能獲得一些缺乏有序組織的零散知識，嚴重影響了他們構建知識體系. 關注單元、章節知識間的聯系，強化主題或板塊教學，可將零散的知識點聚合到一起，實現知識的整合.

教學分析

1. 內容梳理

對學生而言，一次函數屬于常量到變量的一次飛躍，也是生活實際與數學知識間聯系的橋梁，很多生活中的實際問題可揭露函數的本質. 復習教學更能體現知識的結構化特征，是促進學生思維結構化發展的重要機會，將一次函數與相關的知識羅列到一起，可幫助學生從整體的視域更好地理解什么是一次函數，構建模型的同時揭露圖象性質與方程以及不等式間存在怎樣的關聯，完善認知結構.

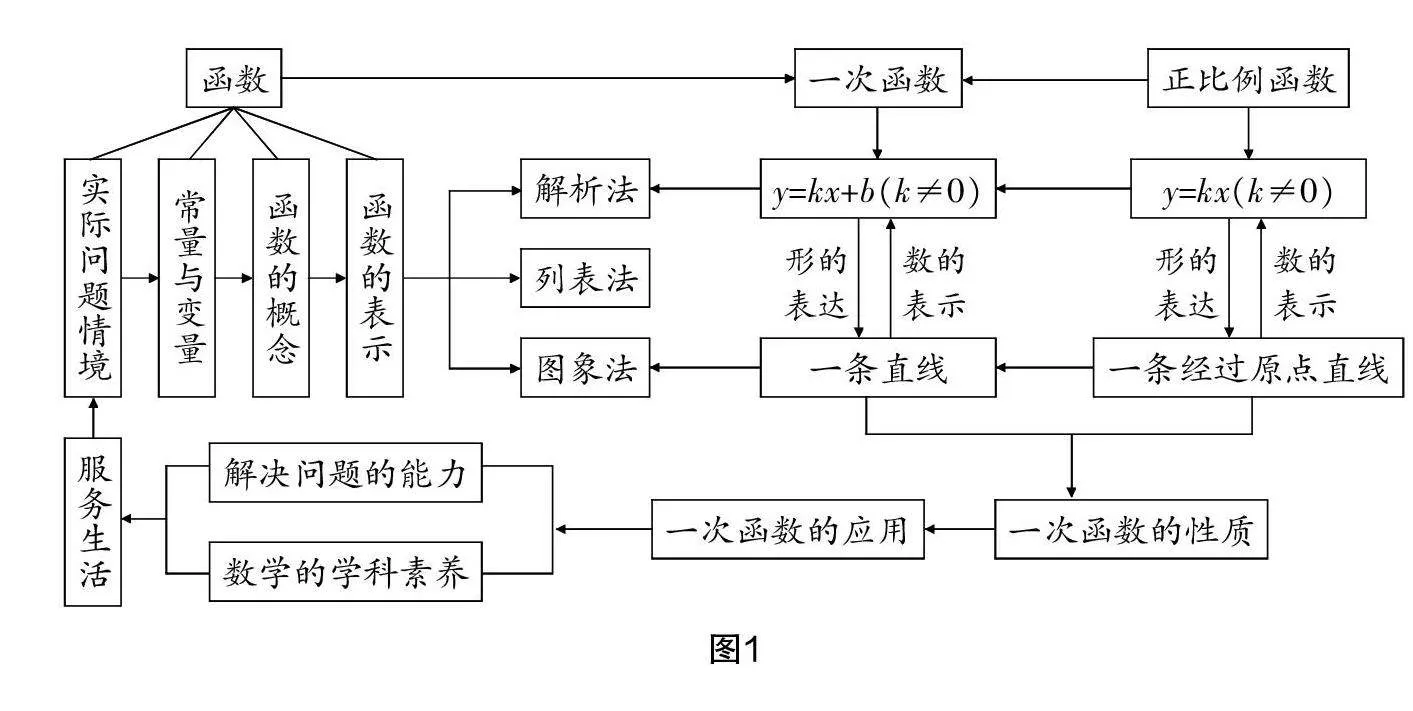
本章節究竟涵蓋了哪些知識點呢？這是課前需搞清楚的問題. 結合《義務教育數學課程標準（2022年版）》筆者對本章節的知識點進行了梳理與總結，形成圖1.

2. 學情調查

部分教師認為本節課并不好上，因為知識點比較多且散，很難將那么多內容聚攏到一起. 為了避免炒冷飯，教師可在課前做一些“功課”，如設計調查問卷充分了解學情.

問卷主要包含了如下幾項內容：①本章節包含的主要內容有概念、圖象與函數的應用等，哪些是你覺得比較容易掌握的？②復習本章節知識，你希望老師在哪些方面給你更多的幫助？如梳理知識點、練習講解或學法指導等. ③你覺得本章節比較難的地方在哪里？如運算、圖象性質或題目比較繁雜等. ④你認為本章節的難度系數有多大，由低到高為1分-5分，你評幾分？⑤面對難題，你怎么辦？⑥你對自己在本章節的學習評價是什么？

調查結論顯示，58%的學生認為一次函數的難度較大，對自己應用一次函數解決問題的能力評價不高，認為自己需要在解題方法與學法指導上得到教師的幫助.

教學設計

1. 開門見山，引入主題

有課前調查作為學情分析的依據，本節課教學目標明確，因此不需要拖泥帶水，課堂伊始教師則可開門見山地帶領學生學習.

師：大家已經學完了一次函數相關知識，本節課我們就針對這一章節的內容進行復習. 首先從知識點方面來看，我們可將一次函數相關的內容聚合到一起，進行整理歸納;其次從記憶方法上來看，想要深刻理解知識點，關鍵在于揭露知識本質，理解各個知識點間的內在聯系. 現在，我們就開啟一次函數的復習之旅.

設計意圖 基于課前調查的結論，設計復習方案，不僅理據清晰，還為基于結構化視域梳理知識、揭露本質做好鋪墊. 開門見山的導入方式簡潔明了，符合初中階段學生身心發展的規律，讓學生對本節課將要探索的內容有了明確的認識.

2. 背景探索，進入狀態

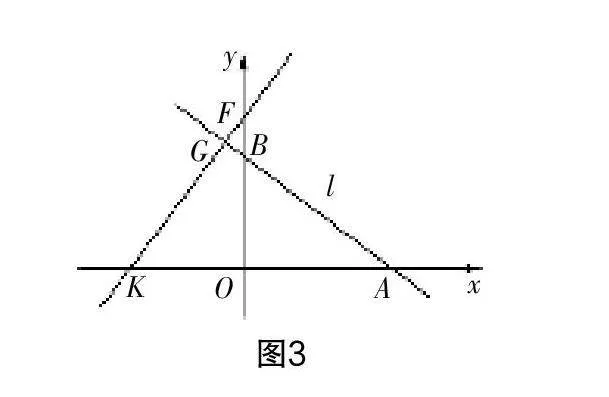
問題 如圖2所示，直線l在直角坐標系內分別和坐標軸相交于點A（8，0）與點B（0，6）. 通過對問題的分析與圖象的觀察，首先讓你想到求什么？

生1：我的第一反應是求直線l的解析式.

師：你會應用哪些知識與方法來求解直線l的解析式呢？

生1：鑒于直線為一次函數的圖象，我會選擇待定系數法來求解直線的解析式.

師：還有補充的嗎？

生2：還可以從數形結合或函數思想等角度來分析直線的解析式.

師：通過你們的描述，可總結為從知識、方法與思想三個層面來獲得直線的解析式.

設計意圖 教師以一個開放性問題成功啟發了學生的思維，讓學生自主進入深度思考與探索狀態，此為一個激趣啟思的過程. 學生從這個問題中感知了直線解析式的數形關系，為形成結構化的思維夯實了基礎. 通過對此問的探索，也讓學生學會從不同的維度分析問題，為形成多元化開放性思維打下基礎.

3. 變式應用，靈活思維

變式1 假設點C位于OA上，以BC為折痕翻折線段OB，使得點O剛好處于AB邊上的點D. 根據這個條件，你首先會想到求什么？

生3：第一反應是求點C的坐標.

師：求點C的坐標需用到哪些知識與解題方法？

生4：可借助全等變換，從勾股定理與設元等角度分析問題.

師：哪位同學能從知識、方法、思想的角度歸納？

生5：知識層面主要涉及圖形的翻折問題，方法層面主要應用到方程和勾股定理，思想層面則涉及全等變換及方程思想.

生6：我的第一反應是求點D的坐標，主要從坐標法出發，具體的解題方法為應用構造思想作坐標軸的垂線.

……

設計意圖 圖形翻折與全等變換有著直接關聯，在坐標系中探索翻折問題的方法較多，但萬變不離其宗，不論問題怎么變化，全等為翻折的本質. 學生積極主動表達自己的想法是思維結構化的外在表現. 學生分析問題的過程是自我反思的過程，反思越深入，對知識本質的理解就越深刻.

變式2 將AB這根線段圍繞點A進行順時針旋轉，當轉到90°時，點B，E剛好重疊. 對此，你最想求什么？

生7：首先想到求點E坐標，過該點向橫軸作垂線，即可揭露點E的具體位置.

師：此過程涉及哪些知識、方法和思想？

生7：知識層面主要涉及求點的坐標、圖形旋轉等;方法層面主要涉及通過垂線構造全等;思想層面主要涉及模型思想與構造思想.

設計意圖 不論是翻折，還是旋轉，均揭露了圖象變換和全等之間的關聯，只要弄清楚朝哪個方向旋轉，問題就能順利解決. 隨著對圖形的探索，進一步深化學生的模型觀念，提升學生的學習力.

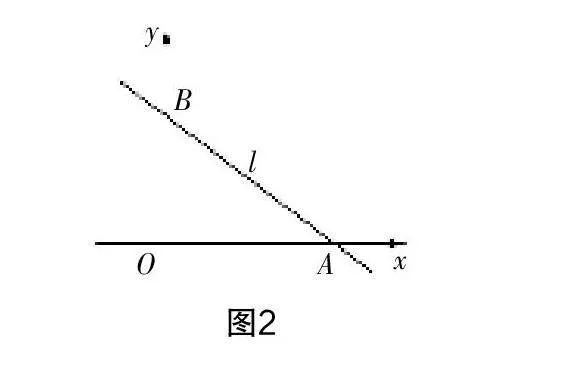
變式3 觀察圖3，若將圖中△ABO圍繞著點O進行逆時針旋轉90°，可得△FKO，若FK與AB交于點G，那么點G的坐標是什么？

生8：想要解決此問，關鍵在于聯立直線FK與直線AB的一次函數關系，構建方程組即可.

師生活動：本題從知識層面來看是求交點問題;從方法層面分析，用到聯立方程的思路;從思想層面來看，主要涉及方程思想等.

設計意圖 隨著復習的推進，學生的思維從研究單線問題逐漸過渡到探索雙線問題，此為一次知識的遷移. 在教師的輔助下，學生對知識、方法和思想進行總結回顧與梳理，在凸顯結構化教學的同時有效揭露了此類問題的本質.

變式4 保持變式3的基本條件不變，添加條件如下：若點M位于AB上，過點O作ON⊥OM，交KF于點N，連接N，M得△NMO，這些條件讓你想到什么問題？

生9：我可以證明△NMO為一個等腰直角三角形，并探究其面積的最小值.

師：非常好！現在我們就圍繞△NMO面積最小值展開討論.

學生合作交流，最終提煉出如下兩類解法：①將求面積最小值的問題轉化成探索直角邊最小值的問題;②借助函數來描述三角形的面積. 隨著探索的深入，學生最終一致認為借助“垂線段最短”實施解題更科學.

設計意圖 這一系列的變式，伴隨著點、線、面的不斷深入研究，成功激活了學生的思維，發展了學生的推理能力，促使學生自主建構出一套解題方法. 難度逐漸增加的四個變式獨具匠心，不僅將課時內容有機地整合成問題，還促使學生的思維在解題過程中逐漸結構化. 學生真正構建了完整的知識體系，對一次函數的認識也更加深入.

教學思考

1. 知識結構是設計教學的載體

復習教學的第一步是厘清知識結構，明確章節所擁有的具體知識，搞清楚知識間的縱橫聯系是揭露知識本質，彰顯結構化教學意義的基本載體. 從整體視域設計結構化復習教學，需將促進學生數學思維螺旋式上升作為基本目標，讓學生在已有經驗的基礎上對所學內容形成新的認知沖突，為進行認知的同化與順應奠定基礎.

從知識、方法與思想三個層面梳理與總結教學內容，不僅能讓學生進一步厘清知識結構，還能讓學生提升對知識的應用意識. 如本節課從一次函數的內容出發，結合各個問題的探索方法與涉及的數學思想，幫助學生構建了完整的知識體系，讓學生真正理解教材編寫的意圖，并對一次函數相關的知識、方法及其實際應用有了深刻的理解.

整體來說，學生學習一次函數不再局限于探索某一個知識或解決某一道試題，而是將思維拓展到知識間的聯系. 拓展問題與應用變式，都是為了促使學生深度學習，最終構建完整的一次函數知識網絡.

2. 學情是確定教學難度的根本

“以學定教”是新課標背景下數學教學的基礎，充分了解學情是確定教學難度的根本，也是構建良好學習結構的關鍵. 所謂的學習結構指根據學生的實際認知水平設計恰當的教學活動，幫助學生構建知識間的內部與外部聯系，其中內部聯系指知識與知識的關聯情況，屬于知識的縱向發展關系;外部聯系指思想方法或學法上的關聯情況，屬于知識的橫向發展關系.

從本節課來看，圖形的平移、旋轉與翻折過程，需學生分別從知識的結構化關聯出發，將問題轉化成關于“關鍵點”定位的分析，此為知識的結構化學習過程，屬于知識、方法、思想等維度的結構化.

鑒于本節課為單元復習課程，需要學生將一章節的內容整合到一起，構建知識間的聯系. 對單個問題的解法探索無法滿足這一目標，而題組模式的解法分析與思想提煉則能彌補單個問題的不足，滿足學生知識體系構建的實際需要. 如拓展變化一個圖形，不僅能鞏固學生原有的知識結構，還能揭露知識本質，讓學生做到知其然且知其所以然.

總之，基于結構化的視角探尋知識本質需經歷一個長期不懈的過程，一節成功的課并不一定是教學手段有多高超，但教學理念一定是先進的. 在復習課型上應用結構化理念實施教學，可幫助學生從整體視域上構建知識體系與研究方法，促使結構化思維的形成，推進數學核心素養的發展.