在問題中探

[摘 要] 新課標強調問題導向下學生自主學習和主動學習，教師一方面需要研究和思考如何設計合情合理的問題指導學生學習，另一方面需要反思指導過程，不斷優化問題的設置，進一步指向學生的再學習和再生長.

[關鍵詞] 問題;反思;初中數學;能力

反思，顧名思義就是回頭、反過來再思考. 在《現代漢語詞典》中解釋為“思考過去的事情、從中總結經驗教訓. ”在學習中，反思就是對學習過程再認識的過程，是獲取知識及形成能力的重要步驟之一. 而在教學中不難發現，反思過程往往容易被師生所忽視，教師過分重視知識的傳遞及問題的講解，很少培養學生的反思能力;學生則習慣于在教師的引導下聽課、刷題，極少花時間主動反思. 另外，“反思”有時候還會被誤解，不少學生會認為只有做錯事情才需要反思，久而久之，師生便陷入了一種“反復講、反復錯”的漩渦，不斷循環著低效的學習.

所謂“授人以魚不如授人以漁”，教會學生反思是發展學生自主學習能力的必要途徑，筆者在多年的教學實踐中逐漸意識到了這一點. 在嘗試對學生的反思型數學能力的培養中，筆者不斷向其他教師請教，自我反思、改進方法，經過一段時間的學習，頗有收獲. 在實踐中，筆者更深刻地體會到了反思在促進學生發展及打造高效課堂中的積極作用. 下文筆者從課前預習、常態課堂、問題教學、階段復習這幾個方面就如何培養學生的反思型數學能力談幾點策略.

課前預習：有效指導，喚醒反思

意識

對初中生而言，課前預習是新課學習的必要環節，通過預習對將要學習的內容先行自學，做到“心中有數”. 但學生往往會因為作業多、時間緊、任務重而輕視預習過程，或者走馬觀花地流于形式. “雙減”實施后，學生的作業負擔相對得到減輕，這正是指導學生高效學習的契機. 反思型能力的培養也正是應從預習開始，教師采用一定的方法指導學生，以喚醒學生的反思意識.

在教學中，筆者與組內教師共同探討制定出了以質疑、反思為主要任務的預習單. 以八年級下冊“一次函數”為例（人教版，下同），設計如下反思型預習單.

課題：19.1 一次函數

預習目標：1. 知道函數的概念.

2. 理解常量與變量的意義.

3. 認識函數的三種表示方法.

預習過程：

1. 自我學習

精讀課本P71-74，明確本節課要學習的內容.

___________________________

2. 自我思考

思考下列問題：

（1）什么是函數？

___________________________

（2）要確定一個變化過程是不是函數，需要從哪幾個方面去判斷？

___________________________

（3）函數中的常量與變量各有怎樣的特征？兩者之間又有怎樣的關系？

___________________________

3. 自我檢測

（1）根據你對函數概念的理解，列舉兩個常見的函數.

___________________________

（2）已知直線m，n之間的距離是3，△ABC的頂點A在直線m上，邊BC在直線n上，求△ABC的面積S和BC邊的長x之間的關系式，并指出其中的變量和常量.

___________________________

4. 自我評價

通過預習，我的收獲是：

___________________________

我的疑惑有：

___________________________

我還想在本節課的學習中獲取的知識有：

___________________________

反思型預習單以反思型問題為主，圍繞“是什么”“為什么”“怎么辦”而展開，從課本內容出發，緊扣課標要求，讓學生明確學習的方向，明晰學習的重點，逐步找準預習的正確方式，養成自我質疑及反思的良好習慣. 在預習單實施的初期，教師需要對學生的完成情況及參與度進行及時的反饋與評價，以便對此及時做出調整與改善. 有效地進行預習指導，旨在喚醒學生的自主反思意識. 反思型預習單的存在只是初級階段，它的“使命”是讓學生知道如何進行反思型預習，進而逐步“消失”，發展成為學生內心主動的預習及反思習慣，讓學生的“學”走在教師的“教”的前面，充分體現學生的主動意識.

常態課堂：情境教學，發展反思

能力

課堂是實施教師“教”與學生“學”的最主要的途徑，也是學生施展能力的舞臺，因此教師需要立足課堂，實抓學生的反思能力，讓課堂成為引導學生反思的主陣地. 因為數學學科本身的特點，常態課往往稍顯“平淡”，無法以豐富的形式及多樣的課堂活動來吸引學生的注意，學生的主動性可能達不到教師的期望. 鑒于此，筆者認為可以采用情境教學的方式，因其易于教師的操作、利于學生的接受，適用于數學常態課的教學. 教師有目的地創設一些具有情緒色彩的、形象生動的場景，讓學生情感上產生共鳴，從而讓抽象的教材內容變得生動形象，使學生的生理機能得到發展，與此同時引導學生主動反思，發展學生的反思能力.

以“一次函數”的教學片段為例.

已知一輛汽車以60 km/h的速度在公路上勻速行駛，行駛里程為s km，行駛時間為t h.

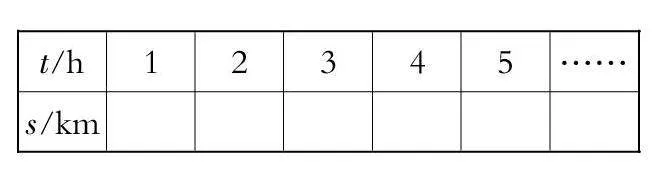
問題1 根據題意填寫下表：

問題2 你能根據題中所給的條件提出問題并進行解答嗎？

反思1 這一過程中有哪些變化的量和不變的量？變化的量有幾個？

反思2 這兩個變化的量之間有什么關系？

問題3 你能根據問題中的量的變化特點再舉出日常生活中的一個常見變化過程嗎？

初涉函數，學生認為其概念抽象而難以理解，因此教師創設日常生活中常見的情境，使復雜的數學知識形象化，并且具有啟發性，激發學生的探究欲望，易于學生的接受，也更有利于學生反思能力的發展. 在上述片段中，學生對問題2的解答基本會圍繞速度、時間、路程的關系來展開，教師應及時對這一變化過程中的變量關系進行追問，引導學生主動反思在這個過程中變量的個數及變量之間的關系. 在此基礎上教師進一步追問問題3，讓學生內化“兩個變量互相聯系，當其中一個變量取定一個值時，另一個變量就有唯一確定的值與其對應”的概念. 在這個過程中，學生體會了對常見問題的質疑、對同一問題不同方面的思考，進而在一定程度上讓自己的反思能力得到了發展.

問題教學：開放問題，激發反思

行為

問題是數學學科最重要的組成元素之一，缺乏問題的數學就仿佛缺少了靈魂. 問題教學法在數學教學中運用非常廣泛，好的問題能夠引發學生深入思考、深度學習. 深度學習的發生可以引起學生的認知沖突，讓學生在不斷的“自我否定”中主動反思. 在“雙減”全面普及的當下，學生的自主性顯得尤為重要，因此開放性問題的設計成為主流，開放的問題可以激發學生自主反思行為的發生，讓學生進行思維的碰撞，摩擦出知識的“火花”.

以下是“一次函數”復習課的片段.

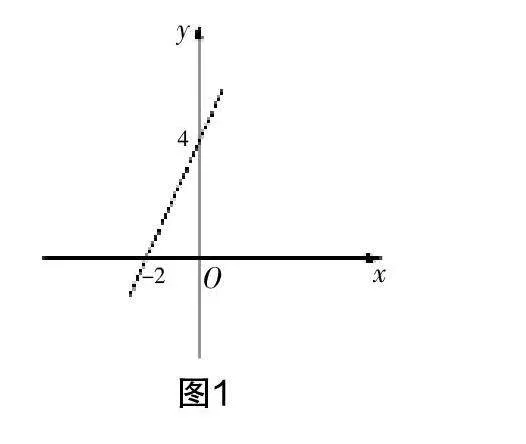
觀察圖1，你能得到哪些信息？

生1：我看到了直線經過（-2，0），（0，4）兩個點，所以它的解析式為y=2x+4.

生2：這是一個一次函數，它經過第一、二、三象限，y隨x的增大而增大. 另外，這條直線交y軸于負半軸.

生3：函數之所以有這樣的特征，取決于一次項系數k和常數項b的正負性.

……

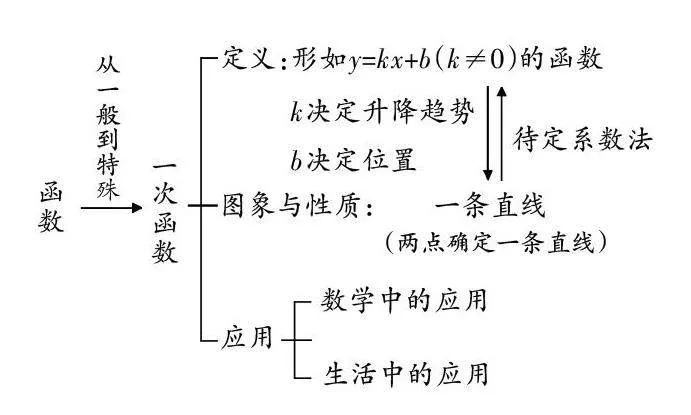
師：從特殊到一般，你能回憶一次函數y=kx+b（k≠0）一章有關的結論嗎？

生4：主要研究一次函數y=kx+b（k≠0）的定義、圖象、性質、應用.

生5：一次函數y=kx+b（k≠0）的圖象是一條直線，是數形結合思想的體現，“從數到形”可以根據k，b的正負性來確定直線的位置;“從形到數”可以根據圖象來判斷k，b的正負性，進一步確定函數解析式.

生6：一次函數的解析式是一條直線，兩點確定一條直線，所以求一次函數的解析式，只要知道兩個點，然后用待定系數法.

師：同學們歸納得非常完整，大家都是基于一次函數的橫向聯系及相應的知識點貫穿起來，并且建構相應的知識網絡.

根據給出的直線圖象，學生不斷地思考，對已有知識進行回顧、收集、加工，提取知識體系中已有的信息，在開放的環境下暢所欲言，反思行為自然發生. 同時，讓學生自己分析問題，可以給教師精準把握學生的能力提供依據，有助于個性化教學的實現. 對于開放性問題，教師千萬要“忍住”，少說話，盡量將展示的機會全部留給學生，只有在學生遇到障礙需要幫助時才給出一點適當的引導，讓學生辯證地看待問題、多方位思考問題，養成及時反思、有效反思的習慣.

階段復習：題組訓練，固化反思

方法

復習階段是反思能力的作用體現最為“活躍”的階段，因為學生需要“喚醒”一個階段所學過的所有知識，將這些知識進行再認識，以此來解決問題. 對原有知識進行加工重組的過程就是反思行為的體現. 在這個過程中，教師需要將關注點置于學生的反思方法上，引導學生深入思考、深層反思，以此固化正確的反思方法. 在此，筆者推薦題組訓練的復習方式，舉一反“n”，讓學生在“沉浸式”訓練中由淺層次的學習向深層次的學習遞進，優化反思行為，對知識的理解更深刻、更完整.

在初三專題復習“最值問題”中設計如下題組.

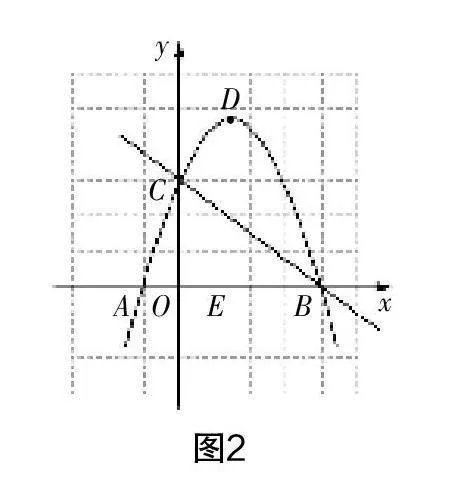
如圖2，已知二次函數y=a（x+2）·（x-8）的頂點為D，與x軸相交于A，B兩點，與y軸相交于C點，一次函數y=kx+6經過B，C兩點，點E的坐標為（1，0）.

（1）求出A，B，C，D各點的坐標及兩個函數的解析式.

（2）在二次函數的對稱軸上找一點P，使得PA+PC最短，求最短距離及點P的坐標;

（3）在直線BC上找一點P，使得△PAO周長最短，求周長及點P的坐標;

（4）在x軸上找一點P，使得PD-PC的值最大，求最大值及點P的坐標;

（5）在直線BC上找一點P，使得PA-PD的值最大，求最大值及點P的坐標;

（6）在直線BC和x軸上各找一點M，N，使得M，N與定點E圍成一個三角形，求當三角形周長最短時M，N的坐標及周長;

（7）在∠ABC的平分線上找一點M，在x軸上找一點N，使得OM+ON最短，求最短值及M，N的坐標;

（8）在直線BC上找一點M，在x軸上找一點N，使得OM+MN最短，求最短值及M，N的坐標;

（9）在△ABC的各邊上各取一點M，N，P，使得△MNP的周長最小，求最小值;

（10）在△ABC的內部內找一點P，使得點P到三角形的三個頂點距離之和最小，求點P的坐標;

（11）在直線y=1和x軸上各找一點M，N，使得CM+MN+NF最短，其中點F為（8，-1），求最短距離及M，N的坐標;

（12）在x軸上有一動線段MN，已知MN=2且M在左側，連接AM，DN，當四邊形CMND的周長最小時，求M，N的坐標.

上述題組由一個圖形出發，涉及兩線段之和最短、三角形周長最小、兩線段之差的絕對值最小、三角形內的點到三角形三個頂點的距離之和最小，內容幾乎輻射到了“共線型最值”的全部類型，讓學生在練習的過程中將這類問題理解透徹，找到這類問題的突破口，以體悟到從問題本身出發進行多角度反思的方法. 復習課的價值就是將零散的知識串聯成“線”，再織成“網”，讓學生在腦海中形成完整的知識體系.

發展反思能力是一種有意識的行為，教師的作用是引導、啟發，而真正能力的形成最終還是建立在學生的自主學習上. 由于學生間的個體差異導致知識的接受能力不盡相同，部分學生對于課堂所講內容無法完全消化或者并非是自己獨立思考而得到的結果，需要在課后及時整理、反思才能真正內化. 因此課后的自主反思對于學生反思能力的形成也有著決定性的作用，錯題分析、反思日記等都能起到相應的作用，當然前期也需要教師的深入追蹤及個性化指導，對此，本文不再贅述.

反思能力的發展不僅是數學學習的要求，還符合其他學科的能力發展特點. 反思型數學能力的養成對學生來說不僅是當下的學習所必需的，更是其一生的學習及成長所必需的. 教師應努力讓學生學會在問題中探索、在反思中進步，以此來發展反思型數學能力，最終學會學習.