星地鏈路中基于毫米波大規模MIMO的混合預編碼算法研究

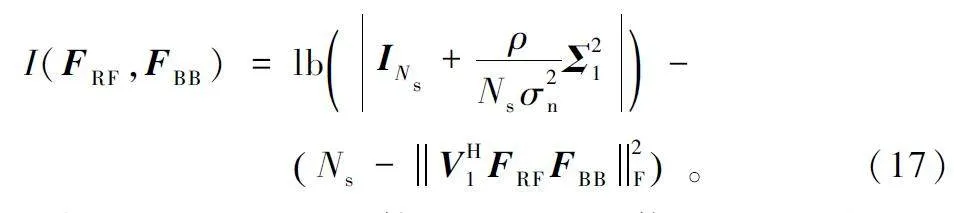
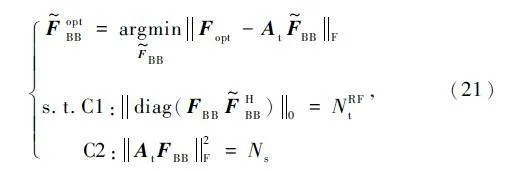
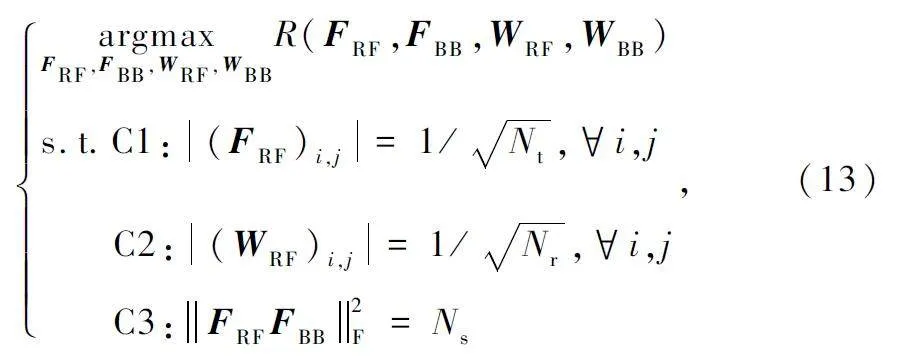
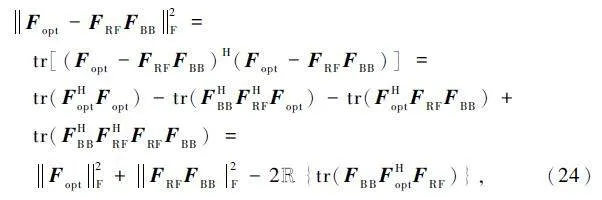
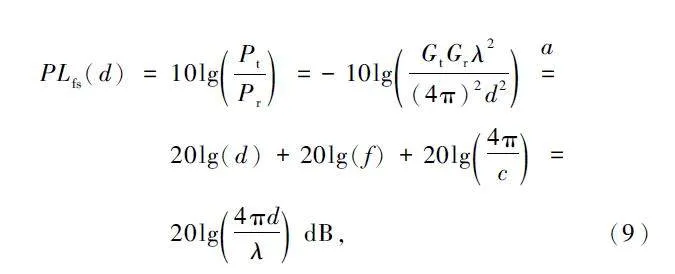
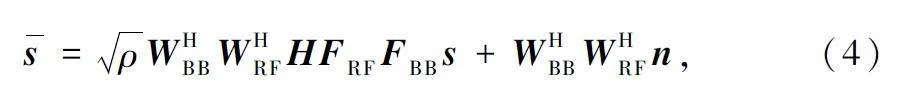
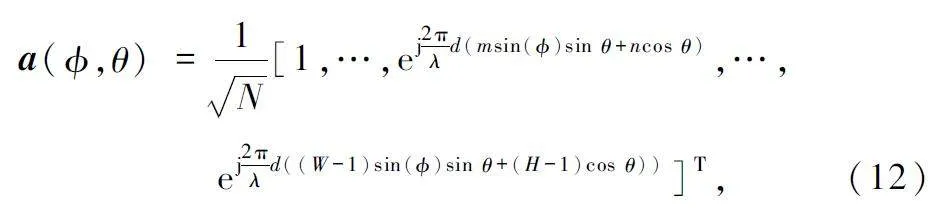
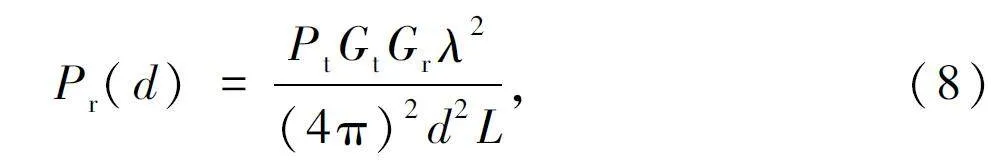
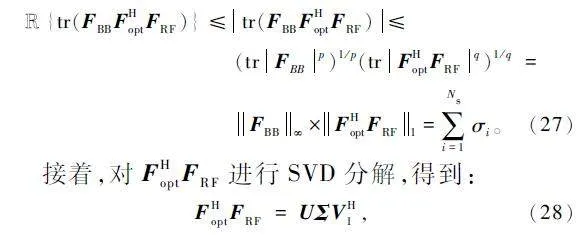
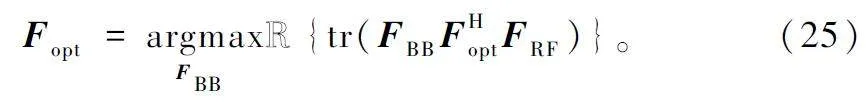
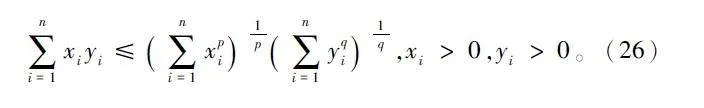
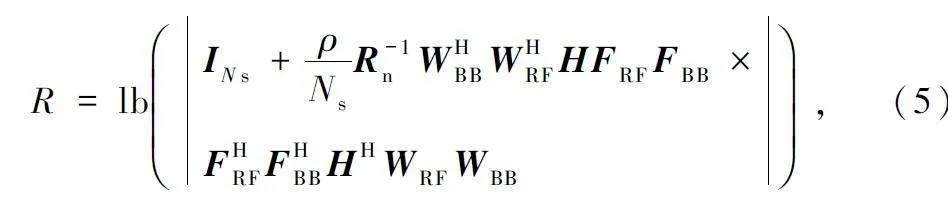
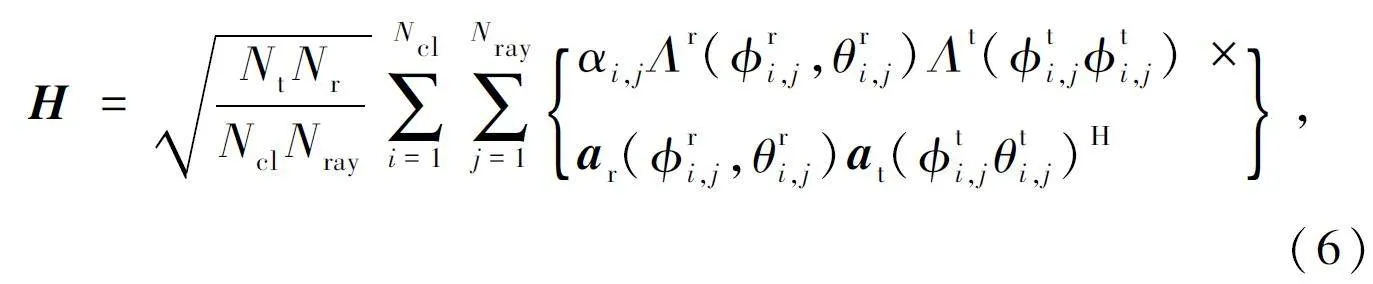
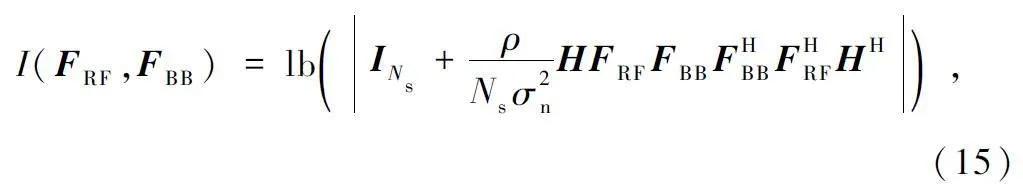
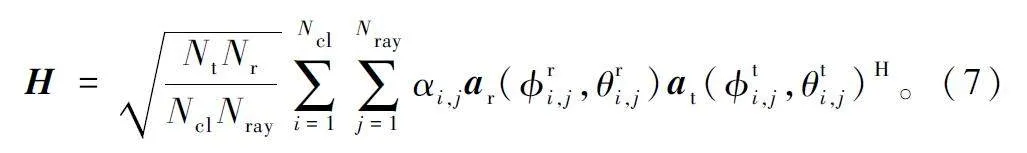
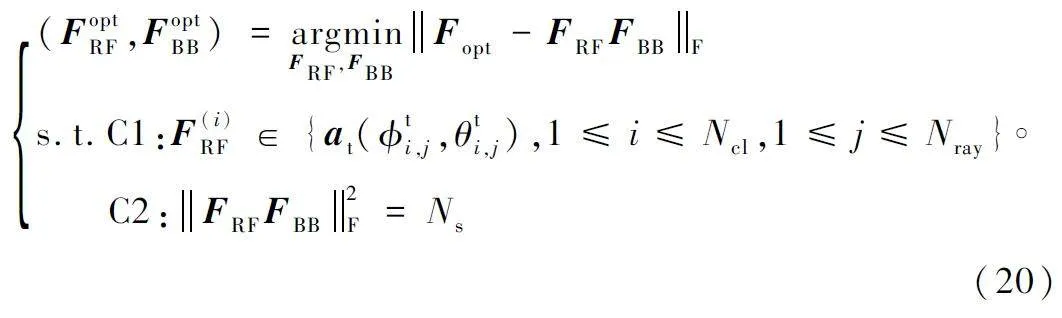
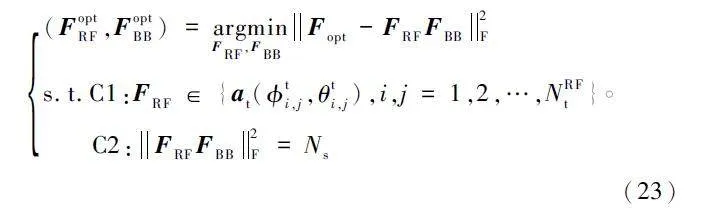
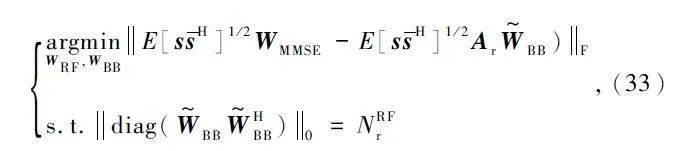
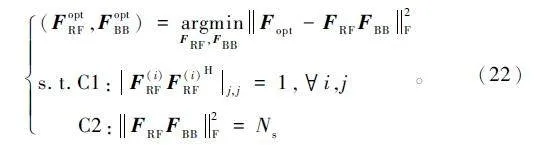
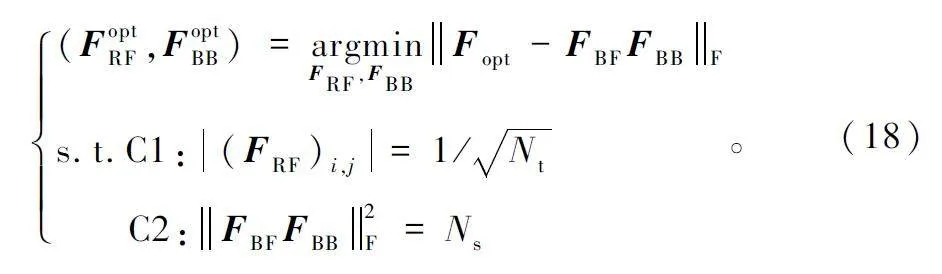
摘 要： 為了提升星地鏈路通信系統頻譜效率，針對毫米波（ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ，ｍｍＷａｖｅ） 大規模多輸入多輸出（Ｍａｓｓｉｖｅ Ｍｕｌｔｉｐｌｅ Ｉｎｐｕｔ Ｍｕｌｔｉｐｌｅ Ｏｕｔｐｕｔ，Ｍａｓｓｉｖｅ ＭＩＭＯ） 系統，在正交匹配追蹤（Ｏｒｔｈｏｇｏｎａｌ Ｍａｔｃｈｉｎｇ Ｐｕｒｓｕｉｔ，ＯＭＰ） 算法的基礎上，提出了一種改進的ＯＭＰ （Ｉｍｐｒｏｖｅｄ-ＯＭＰ） 混合預編碼算法。針對星地鏈路間通信的特定場景，引入了基于擴展的Ｓａｌｅｈ-Ｖａｌｅｎｚｕｅｌａ （Ｓ-Ｖ） 信道模型；針對ＯＭＰ 算法中求解模擬預編碼矩陣時存在迭代次數過多的問題，在結合多步長思想的基礎上，從天線陣列響應集合中選取與射頻鏈路（Ｒａｄｉｏ Ｆｒｅｑｕｅｎｃｙ Ｃｈａｉｎｓ，ＲＦ Ｃｈａｉｎｓ） 相等的前多列作為模擬預編碼矩陣；為了克服ＯＭＰ 算法中的偽逆運算復雜度較高的問題，結合矩陣分解和Ｈ-ｌｄｅｒ 不等式簡化了數字預編碼的求解。仿真結果表明，在理想的信道狀態信道條件下，當ＲＦ Ｃｈａｉｎｓ 的數量和數據流的數量之間的差距較小時，Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法可以獲得更優的性能。Ｉｍｐｒｏｖｅｄ-ＯＭＰ 方案有效地降低了計算復雜度。

關鍵詞：星地鏈路；大規模多輸入多輸出；毫米波；混合預編碼；ＩｍｐｒｏｖｅｄＯＭＰ 算法

中圖分類號：ＴＮ９２９． ５ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１０６（２０２４）０５－１０６３－１１

０ 引言

衛星網絡具有覆蓋面廣、基礎設施獨立和抗破壞能力強等突出優勢，與地面網絡具有極強的互補關系，近年來受到學術界和工業界的廣泛關注［１］。衛星網絡能夠為偏遠地區和非陸地地區等區域提供冗余覆蓋［２］，實現全球無縫通信覆蓋。衛星覆蓋范圍大，但單星容量受限，單位面積能夠提供的通信容收稿量較低。因此，如何提升頻譜效率、實現更大的通信容量是當前衛星網絡的熱點研究問題。

提高系統容量的一種方法是通過物理層技術提高頻譜效率，如以大規模多輸入多輸出（ＭａｓｓｉｖｅＭｕｌｔｉｐｌｅ Ｉｎｐｕｔ Ｍｕｌｔｉｐｌｅ Ｏｕｔｐｕｔ，Ｍａｓｓｉｖｅ ＭＩＭＯ）［３］為代表的空分復用技術［４］。預編碼作為一種基于Ｍａｓｓｉｖｅ ＭＩＭＯ 天線陣列的信號預處理技術，通過調整天線陣列中陣元的加權系數，可以產生具有指向性的波束，能夠補償無線信號的衰落和失真，有效地提升通信系統的質量，對于提高信道增益和保障通信質量具有十分重要的意義，已經在地面移動通信系統中得到廣泛的研究和應用［５］。

文獻［５］提出了混合預編碼架構，只需要較少的射頻鏈路（Ｒａｄｉｏ Ｆｒｅｑｕｅｎｃｙ Ｃｈａｉｎｓ，ＲＦ Ｃｈａｉｎｓ）和移相器，就能夠有效降低系統功耗和硬件成本，并能達到接近全數字預編碼的性能［６－７］。此外，根據ＲＦＣｈａｉｎｓ 到天線的映射方式不同，混合預編碼架構可分為全連接和部分連接結構。全連接結構的每條ＲＦ Ｃｈａｉｎｓ 連接到所有天線，能夠享有每條ＲＦＣｈａｉｎｓ 的全部波束賦形增益，具有較好的系統性能，但復雜度較高；部分連接結構中每一根ＲＦ Ｃｈａｉｎｓ僅與部分天線相連接，以犧牲一部分系統性能來換取較低的復雜度，但系統性能相對較差。

針對地面網絡場景的混合預編碼，國內外學者已經進行了廣泛研究。文獻［８］在充分考慮毫米波（ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ，ｍｍＷａｖｅ）通信的稀疏散射特性和大規模天線陣列相關性的基礎上，將頻譜效率優化問題轉化為一個含有約束的稀疏矩陣重構問題，提出了基于正交匹配追蹤（Ｏｒｔｈｏｇｏｎａｌ ＭａｔｃｈｉｎｇＰｕｒｓｕｉｔ，ＯＭＰ）的混合預編碼算法，有較好的系統性能的ＯＭＰ 算法采用發射天線的陣列響應矢量作為模擬預編碼矩陣的候選矢量集，在迭代過程中存在大量偽逆運算，計算復雜度較高。為此，文獻［９］提出了一種低復雜度混合預編碼方案，通過對ＯＭＰ 的碼本集合進行奇異值分解（Ｓｉｎｇｕｌａｒ Ｖａｌｕｅ Ｄｅｃｏｍｐｏｓｉｔｉｏｎ，ＳＶＤ），并選擇分解后的右奇異矩陣較大特征值的特征向量作為碼本，在此基礎上獲得更多相關向量來擴大碼本，從中獲取模擬預編碼矩陣的相位信息，避免了迭代搜索。文獻［１０］借助ＯＭＰ 算法直接求出模擬預編碼矩陣，然后通過均值迭代計算數字預編碼矩陣，而不需要進行ＳＶＤ 運算，在提升了系統頻譜效率的同時降低了復雜度。文獻［１１］針對ＲＦ Ｃｈａｉｎｓ 數量和數據流數量之間的關系進行了研究，當ＲＦ Ｃｈａｉｎｓ 數量大于２ 倍的數據流時，證明了在單用戶和多用戶Ｍａｓｓｉｖｅ ＭＩＭＯ 系統中，基于全連接架構的混合預編碼理論上能夠達到理想全數字預編碼系統的性能。與文獻［８ －９］不同，喻翔浩等［１２］提出了一種基于相位提取的交替最小化（Ｐｈａｓｅ Ｅｘｔｒａｃｔｅｄ Ａｌｔｅｒｎａｔｉｎｇ Ｍｉｎｉｍｉｚａｔｉｏｎ， ＰＥ-ＡｌｔＭｉｎ）混合預編碼算法。該算法在每次迭代中交替優化數字和模擬預編碼器直到收斂，通過對數字預編碼矩陣增加一個正交約束來降低算法復雜度，在ＲＦ Ｃｈａｉｎｓ 數量與數據流數相同時，系統達到最優性能，但仍然具有一定的局限性。

鑒于混合預編碼技術在地面移動網絡中的成功應用［８－１２］，如何拓展到衛星通信網絡中，對于衛星－地面融合網絡的建設具有重要意義［１３］。文獻［１４］針對衛星通信場景，研究了Ｍａｓｓｉｖｅ ＭＩＭＯ 傳輸的可行性，就全連接和部分連接結構分別提出了用于衛星機載處理的混合預編碼方案。文獻［１５］針對相控陣天線在衛星通信場景中的發展趨勢進行了展望。在此基礎上，文獻［１６］提出了一種適用于低軌（Ｌｏｗ Ｅａｒｔｈ Ｏｒｂｉｔ，ＬＥＯ）衛星通信系統的混合預編碼架構。文獻［１７］針對ＬＥＯ 衛星通信場景，提出了基于能效最大化的混合預編碼方案，實現了下行Ｍａｓｓｉｖｅ ＭＩＭＯ ＬＥＯ 衛星高效傳輸，但沒有考慮系統頻譜效率的優化問題。文獻［１８］針對５Ｇ 衛星集成網絡（Ｓａｔｅｌｌｉｔｅ Ｉｎｔｅｇｒａｔｅｄ Ｎｅｔｗｏｒｋ，ＳＩＮ）場景，研究了ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 系統中的混合預編碼問題，以較少的迭代次數提高整體頻譜效率，實現了性能和復雜性之間的平衡，但系統性能仍有待提升。此外，文獻［１９］探討了衛星系統預編碼的發展概況，就不同場景下預編碼理論的發展提供了新的見解。

為避免衛星網絡與地面網絡之間的同頻干擾，衛星網絡需要采用頻率更高的ｍｍＷａｖｅ 頻段實現星地鏈路間的通信［２０］。由于星地鏈路與地面移動通信網絡的通信頻段和信道條件不同，地面網絡中基于Ｍａｓｓｉｖｅ ＭＩＭＯ 的傳統預編碼技術無法直接應用于星地鏈路通信場景［１８］。本文針對星地鏈路ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 系統的單用戶場景，提出了一種改進的ＯＭＰ （Ｉｍｐｒｏｖｅｄ-ＯＭＰ ）混合預編碼算法，在有效降低復雜度的基礎上，當數據流為１、２ 和４時，系統性能分別提升了１． ６６％ 、３． ５５％ 和１２． ８％ 。

１ 系統模型

１． １ 混合預編碼系統模型

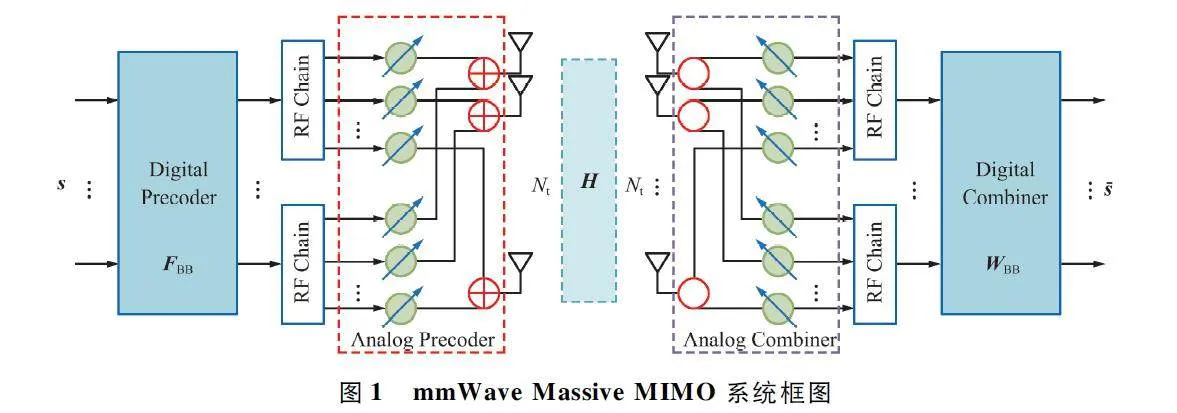
考慮星地鏈路ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 系統的下行鏈路場景，即衛星發送信號至地面用戶的場景，假設衛星側配備Ｎｔ 根發射天線和ＮＲＦｔ 根ＲＦＣｈａｉｎｓ，發送Ｎｓ 路數據流到地面用戶，接收端配備Ｎｒ 根發射天線和ＮＲＦｒ 根ＲＦ Ｃｈａｉｎｓ。與傳統的ＭＩＭＯ 系統不同，ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 系統中ＲＦ Ｃｈａｉｎｓ 的數目應小于天線數目，即Ｎｓ ≤ ＮＲＦｔ ≤Ｎｔ。連接結構ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 系統如圖１所示。

在通信過程中，從衛星側發送Ｎｓ 條數據流，依次經過數字預編碼器ＦＢＢ 和模擬預編碼器ＦＲＦ 后，調相到天線發射單元，經過處理后的發射信號ｘ 可以表示為：

ｘ ＝ ＦＲＦ ＦＢＢ ｓ， （１）

式中：ｓ 為Ｎｓ ×１ 維的數據流。

Ｅ［ｓｓＨ ］ ＝ ＩＮｓ ／ Ｎｓ 。（２）

為了滿足發送功率限制，數字預編碼矩陣和模擬預編碼矩陣應滿足：

｜｜ＦＲＦ ＦＢＢ｜｜２Ｆ ＝ Ｎｓ 。（３）

假設信道狀態信息（Ｃｈａｎｎｅｌ Ｓｔａｔｕｓ Ｉｎｆｏｒｍａｔｉｏｎ，ＣＳＩ）已知，則接收信號ｓ 可以表示為：

式中：ｎ 為加性高斯噪聲，且ｎ ～CN （０，σ２ｎ ＩＮｓ ）；ＷＲＦ和ＷＢＢ 分別為模擬組合矩陣和數字組合矩陣。此時，系統的頻譜效率可以表示為：

式中：Ｒｎ ＝ σ２ｎ ＷＨＢＢ ＷＨＲＦ ＷＲＦ ＷＢＢ 為噪聲協方差矩陣。

１． ２ 信道模型

對于星地鏈路中的ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 系統而言，由于ｍｍＷａｖｅ 在自由空間存在嚴重的路徑損耗，導致有限空間的選擇性或稀疏的散射特性。同時衛星側部署的大規模天線陣列使得天線陣元之間高度相關。因此，本文采用擴展ＳａｌｅｈＶａｌｅｎｚｕｅｌａ（ＳＶ）窄帶簇信道模型，該模型已經被證明可提供精確的窄帶ｍｍＷａｖｅ 信道數學模型［２１］。信號從衛星側發出傳播到地面用戶，則衛星與地面用戶之間的信道矩陣可以表示為：

式中：αｉ，ｊ 為第ｉ 個簇中的第ｊ 條徑的信道復增益，服從復高斯分布CN（０，σ２α，ｉ ）的獨立同分布的隨機變量，且ΣＮ ｃｌｉ ＝ １ σ２α，ｉ ＝ Ｎｃｌ，從而歸一化信道矩陣使其滿足Ｅ［ ||Ｈ|| ２Ｆ］＝ Ｎｔ Ｎｒ［２２］；ａｒ（Φｒｉ，ｊ，θｒｉ，ｊ）和ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ）分別為接收端和發射端天線陣列響應向量，為Ｎｒ ×Ｎｃｌ Ｎｒａｙ和Ｎｔ ×Ｎｃｌ Ｎｒａｙ 維矩陣；Φｒｉ，ｊ（θｒｉ，ｊ）和Φｔｉ，ｊ（θｔｉ，ｊ）分別為第ｉ 個簇中第ｊ 條徑的到達和離開的水平（垂直）角，且服從拉普拉斯分布［２３］；Λｒ（Φｒｉ，ｊ，θｒｉ，ｊ ）和Λｔ（Φｔｉ，ｊ，θｔｉ，ｊ ）分別對應接收天線和發射天線在到達角（Ａｎｇｌｅ ｏｆＡｒｒｉｖａｌ，ＡｏＡ）和離開角（Ａｎｇｌｅ ｏｆ Ｄｅｐａｒｔｕｒｅ，ＡｏＤ）時的增益，假定每個天線單元具有單位增益。因此，Ｓ-Ｖ 信道模型可以簡化為：

對于星地鏈路通信場景，衛星與用戶之間不存在任何障礙物，一般可以視為視距傳輸，自由空間損耗是影響星地鏈路中最主要的因素。因此，通常用自由空間傳播模型表征星地鏈路中的損耗，根據Ｆｒｉｉｓ 公式，有：

式中：Ｐｔ 和Ｐｒ 分別為發射功率和接收功率，λ 為波長，Ｇｔ 和Ｇｒ 分別為發射天線增益和接收天線增益，Ｌ 為與傳播環境無關的系統損耗參數，ｄ 為傳播距離。在星地鏈路模型中，假設Ｌ ＝ １，即無系統損耗的自由空間路徑損耗ＰＬｆｓ 計算如下：

式中：ａ 表示當Ｇｔ ＝ Ｇｒ ＝ １。

設γ 為星地鏈路中的衰減系數，包括自由空間路徑損耗ＰＬｆｓ、大氣損耗ＰＬａｔ 和雨衰影響ＰＬｒａ 等，因此γ 可以表示為：

γ ＝ ＰＬｆｓ ＋ ＰＬａｔ ＋ ＰＬｒａ 。（１０）

對于γ，其與衛星軌道高度ｄ、電磁波波長λ、發射天線增益Ｇｔ、接收天線增益Ｇｒ 以及大氣損耗ＰＬａｔ和雨衰ＰＬｒａ 相關。對于單用戶星地鏈路可以視為點對點通信，在軌道高度一定的前提下，其傳輸過程屬于遠距離傳輸，到達用戶端的時間唯一確定，多經效應并不明顯。在用戶端的接收功率因γ 的不同而不同，衰減系數γ 可以視為常數進行處理，在仿真對參數進行設置即可。因此，可以得到基于ＳＶ 擴展的星地鏈路信道模型：

Ｈｓｔ ＝ γ·Ｈ。（１１）

１． ３ 天線陣列模型

在ｍｍＷａｖｅ 通信系統中，使用均勻平面陣列（Ｕｎｉｆｏｒｍ Ｐｌａｎａｒ Ａｒｒａｙ，ＵＰＡ）天線更為適合，主要有以下原因［８］：

① 將天線單元在平面進行部署，可以減小天線陣列的尺寸；

② 平面天線陣列更有利于天線單元的封裝；

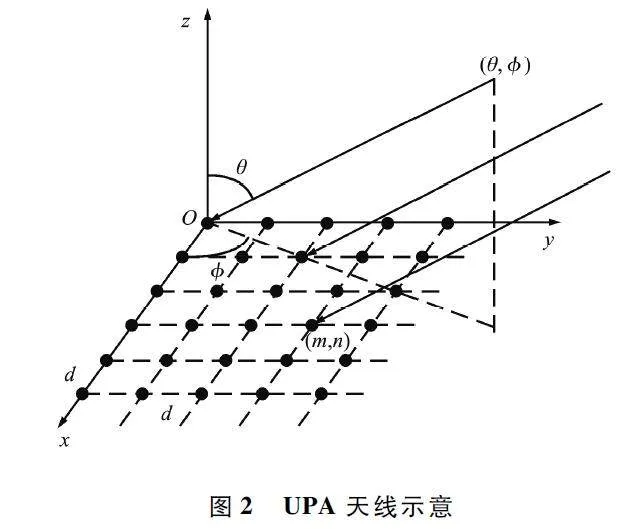
③ 平面陣列能夠在水平方向和垂直方向實現波束賦形，而均勻線性陣列（Ｕｎｉｆｏｒｍ Ｌｉｎｅａｒ Ａｒｒａｙ，ＵＬＡ）只能在單一方向上實現波束賦形。ＵＰＡ 天線示意如圖２ 所示。

對于ＵＰＡ，在ｘｙ 平面內，若在ｘ 軸和ｙ 軸分別有Ｗ 和Ｈ 個天線陣元，則ＵＰＡ 天線陣列響應矢量可以表示為：

式中：ｍ 和ｎ 分別表示ＵＰＡ 天線陣列的行、列索引變量，滿足１≤ｍ≤Ｗ，１≤ｎ≤Ｈ，且Ｎ ＝ ＷＨ；ｄ 表示天線間距，λ 表示波長。

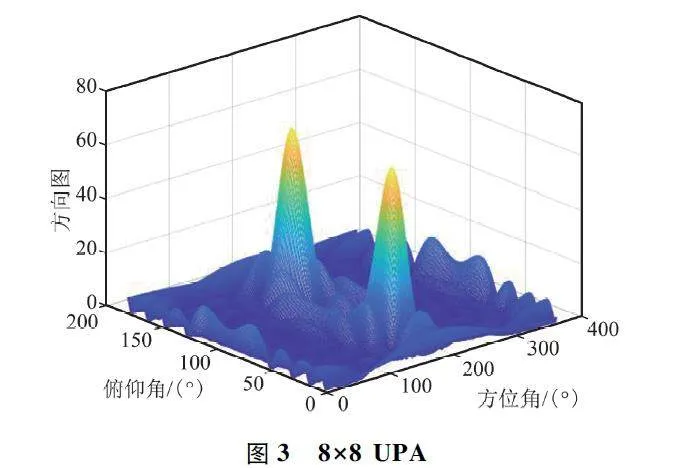
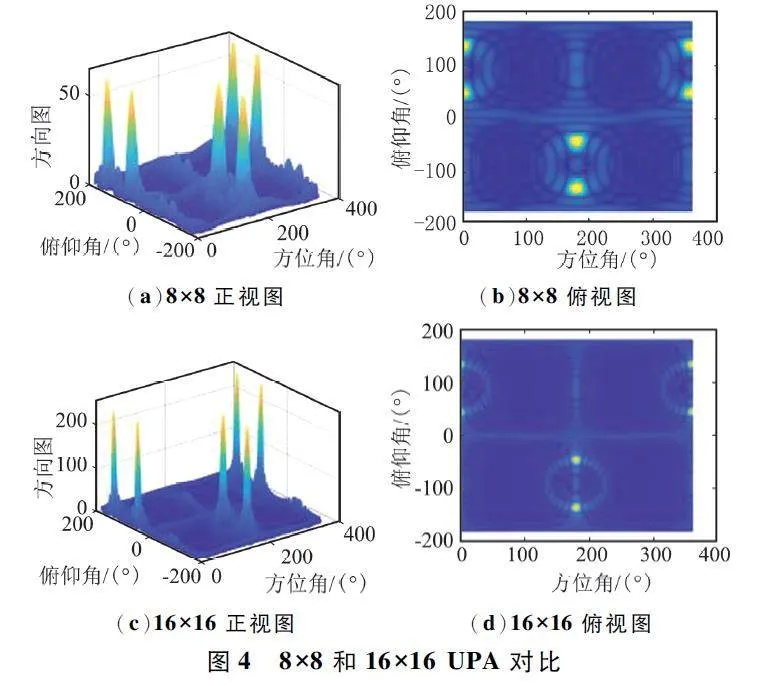
為了形象地展示ＵＰＡ 天線的性質和優點，本文給出了不同天線陣列配置下的仿真結果。圖３ 給出了天線陣列配置為（８，８）時波束指向為（４５°，１８０°）的波束正視圖，俯仰角和方位角的范圍分別為（０°，１８０°）和（０°，３６０°）。作為對比，圖４ 給出了天線陣列配置分別為（８，８）和（１６，１６）時波束指向為（４５°，１８０°）的波束正視圖和波束俯視圖，俯仰角和方位角的范圍分別為（－１８０°，１８０°）和（０°，３６０°）。

由圖３ 和圖４ 可以看出，隨著天線陣列中陣元數量的增加，波束變得細窄且更具有指向性，同時方向圖幅度也隨著陣元數量增加而明顯提升。

２ 問題建模

基于上述模型，星地鏈路ｍｍＷａｖｅ ＭａｓｓｉｖｅＭＩＭＯ 系統下行鏈路的數字預編碼和模擬編碼的聯合設計問題可以描述為：

式中：Ｒ 為系統頻譜效率，ＦＲＦ 和ＦＢＢ 分別為數字預編碼矩陣和模擬預編碼矩陣，ＷＲＦ 和ＷＢＢ 分別為模擬組合矩陣和數字組合矩陣。約束條件Ｃ１ 和Ｃ２表示恒模約束，Ｃ３ 表示發射端功率約束。針對式（１３）中的優化問題，由于ＦＲＦ 和ＷＲＦ 具有恒模約束，要聯合優化極為困難。假設接收端能夠實現完美譯碼，該問題可以解耦為混合預編碼設計和混合合并設計問題［８］。本文主要關注發射端混合預編碼的設計，則數字預編碼器和模擬編碼器的聯合設計可以重述如下：

進一步，為了尋找最優的模擬預編碼矩陣和數字預編碼矩陣，轉化為最大化衛星發送側的互信息量：

并對信道矩陣Ｈ 進行ＳＶＤ。

Ｈ ＝ ＵΣＶＨ 。（１６）

根據文獻［８］，對奇異值矩陣Σ 和Ｖ 替換后，目標函數可以進一步簡化為：

由式（１７）可知，要使衛星側互信息量最大，需要使ｔｒ （ＶＨ１ ＦＲＦ ＦＢＢ ）最大。對于此類問題，通過使||Ｆｏｐｔ －ＦＲＦ ＦＢＢ||Ｆ 最小來最大化ｔｒ（ＶＨ１ ＦＲＦ ＦＢＢ ），因此上述問題可以進一步等價為：

由式（１８）可知，對于單用戶ｍｍＷａｖｅ ＭａｓｓｉｖｅＭＩＭＯ 系統，混合預編碼就是尋求最優的模擬預編碼矩陣和數字預編碼矩陣，使其盡可能接近于純數字預編碼矩陣，即滿足：

Ｆｏｐｔ ≈ ＦＲＦ ＦＢＢ 。（１９）

針對此問題，已經有相關研究人員和學者從不同角度，給出了相應的解決方案，接下來主要介紹ＯＭＰ［８］和基于ＯＭＰ 改進的混合預編碼算法以求解上述問題。

３ 混合預編碼算法設計

３． １ 基于ＯＭＰ 的混合預編碼算法

針對類似優化問題，文獻［８］提出了基于ＯＭＰ的稀疏空間混合預編碼算法，該算法利用ｍｍＷａｖｅ信道的稀疏特性，將數字預編碼的設計轉化為稀疏約束矩陣重構問題。

ＯＭＰ 算法的本質是在ＦＲＦ 的碼本集合約束下，求解Ｆｏｐｔ 在混合預編碼器集合構成的子空間上的最佳逼近。因此，基于ＯＭＰ 算法的混合預編碼問題表述如下：

由式（２０）可以看出，ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ）幅度恒定且是一個僅與相位有關的向量，這與模擬預編碼器所要求的恒模約束相符合，因此可以利用ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ ）的線性組合來實現模擬預編碼器，上述問題可以進一步轉化為：

式中：Ａｔ ＝ ［ａｔ（Φｔ１，１ ，θｔ１，１ ），…，ａｔ（ΦｔＮｃｌ，Ｎｒａｙ，θｔＮｃｌ，Ｎｒａｙ ）］∈ＣＮｃｌ×Ｎｒａｙ為天線陣列響應向量，模擬預編矩陣中的元素都從Ａｔ 其中選取；～Ｆ ＢＢ ∈Ｎｃｌ Ｎｒａｙ ×Ｎｓ 為混合預編碼矩陣的數字預編碼部分， 稀疏約束||ｄｉａｇ（ＦＢＢ～Ｆ ＨＢＢ ）|| ０ ＝ ＮＲＦｔ 表明限制ＦＢＢ 的非零行不能大于ＮＲＦｔ ，即當ＦＢＢ 中含有ＮＲＦｔ 個非零行時，Ａｔ 中有ＮＲＦｔ 列被選中。因此可得，ＦｏｐｔＢＢ 由Ｆ ～ ｏｐｔＢＢ 中的ＮＲＦｔ 個非零行構成，ＦｏｐｔＲＦ 為Ａｔ 中對應的ＮＲＦｔ 列。基于ＯＭＰ的混合預編碼算法如下。

需要注意的是，ＯＭＰ 算法需要預先設計好模擬預編碼矩陣的候選集，計算量較大。此外，當數據流較多的時候，會引起數據流之間的干擾，不適合多數據流傳輸的情況。

３． ２ 基于ＩｍｐｒｏｖｅｄＯＭＰ 的混合預編碼算法

上文提出的基于ＯＭＰ 的混合預編碼算法，無法同時兼顧系統頻譜效率和復雜度，主要體現在：一方面，ＯＭＰ 算法需要提前知道發射端的天線陣列響應向量，在求解混合預編碼矩陣時需要進行復雜的迭代更新，并且該算法僅僅適用于數據流較少的情況，當ＲＦ Ｃｈａｉｎｓ 數量小于２ 倍Ｎｓ 時，ＯＭＰ 性能較差，無法推廣至數據流較大的場景；另一方面，存在大量迭代運算，算法的復雜度較高。

因此，本文在綜合考慮系統性能和算法復雜度的前提下，提出了一種基于Ｉｍｐｒｏｖｅｄ-ＯＭＰ 的混合預編碼算法。由于發射端和接收端的情況類似，因此，本文只考慮發送端的混合預編碼設計。

Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法的主要思想：對模擬預編碼矩陣和數字預編碼矩陣進行解耦，即先固定數字預編碼矩陣求解模擬預編碼矩陣，然后利用所求解的模擬預編碼矩陣來設計數字預編碼矩陣。ＩｍｐｒｏｖｅｄＯＭＰ 結合了多步長的思想，從天線陣列響應集合中選取與ＲＦ Ｃｈａｉｎｓ 相等的前ＮＲＦｔ 列構成模擬預編碼矩陣；然后，結合矩陣分解和Ｈ-ｌｄｅｒ 不等式簡化了數字預編碼的求解過程。

基于擴展的Ｓ-Ｖ 信道模型和ｍｍＷａｖｅ ＭａｓｓｉｖｅＭＩＭＯ 系統傳輸模型，給出優化目標函數：

３． ２． １ 模擬預編碼器設計

為了使混合預編碼矩陣在最優全數字預編碼矩陣上的投影最大，首先給出引理１［１０］：最優預編碼矩陣Ｆｏｐｔ 的列向量是ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ ），?ｉ，ｊ 的線性組合，天線陣列響應矢量ａｔ （Φｔｉ，ｊ，θｔｉ，ｊ ），?ｉ，ｊ 為Ｎｔ ×Ｎｃｌ Ｎｒａｙ 維矩陣。

根據引理１ 和ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 信道模型的特性，ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ ），?ｉ，ｊ 與模擬預編碼矩陣具有相似結構，同時ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ），?ｉ，ｊ 和最優混合預編碼矩陣的列相關。因此，選取ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ ），?ｉ，ｊ的前ＮＲＦｔ 列作為最優模擬預編碼矩陣，從而使其與最優混合預編碼矩陣前ＮＲＦｔ 列的相關性最強。這樣避免了復雜的迭代更新運算，大大降低了系統實現復雜度。所以，上述問題可以轉化為：

３． ２． ２ 數字預編碼器設計

根據Ｆｒｏｂｅｎｉｕｓ 范數的定義，首先對式（２３）中的目標函數進行化簡：

式中：模擬預編碼矩陣ＦＲＦ 已經在上一步的設計中通過ａｔ（Φｔｉ，ｊ，θｔｉ，ｊ），?ｉ，ｊ 獲得，同時預編碼矩陣需要滿足功率約束ＦＲＦ ＦＢＢ２Ｆ ＝ Ｎｓ，且最優預編碼矩陣Ｆｏｐｔ２Ｆ ＝ Ｎｓ。因此，進一步將目標函數進行改寫：

為了得到數字預編碼矩陣，本文根據Ｈoｌｄｅｒ 不等式和數字預編碼矩陣的正交特性，對式（２５）進一步化簡。為此，給出引理２：給定ｐ＞１，假設１/ｐ ＋１/ｑ＝１，則有：

根據Ｆｒｏｂｅｎｉｕｓ 范數及Ｈｌｄｅｒ 不等式，式（２５）可以進一步化簡為：

式中：Σ 為由前Ｎｓ 個非零奇異值組成的對角陣。

在式（２７）中，當且僅當ＦＢＢ ＝ Ｖ１ ＵＨ 時，等號成立，不等式轉變為等式，此時式（２７）獲得最大值。即通過Ｈｌｄｅｒ 不等式和Ｆｒｏｂｅｎｉｕｓ 范數逼近優化目標函數的最優值，得到最優的數字預編碼矩陣。

綜上可知，基于ＩｍｐｒｏｖｅｄＯＭＰ 的混合預編碼算法結合多步長的思想，通過選取與ＲＦ Ｃｈａｉｎｓ 數量相等的最優列構成模擬預編碼矩陣，將步長從１ 增加為ＲＦ Ｃｈａｉｎｓ 路數，整體迭代次數降低；此外，利用Ｈｌｄｅｒ 不等式和矩陣范數的正交特性逼近最優目標函數，求解最優數字預編碼矩陣。ＩｍｐｒｏｖｅｄＯＭＰ 算法具體如下。

３． ３ 接收端基于ＩｍｐｒｏｖｅｄＯＭＰ 的合并設計

通常情況下，接收端的合并矩陣包括模擬合并矩陣和數字合并矩陣的設計，一般可以通過最小化發射信號與接收信號之間的均方誤差進行設計合并矩陣ＷＲＦ ＷＢＢ 。

因此，接收端合并矩陣的設計問題可以表述為：

在式（３２）中，由于發射端的ＦＲＦ 和ＦＢＢ 是在假設接收端組合器是完美狀態下進行求解的，發射端與接收端是保持解耦狀態，因此接收端的優化問題可以通過采用與混合預編碼器相同的方法進行設計。為此，進一步將上式進行展開得到：

式中：Ａｒ ＝ ［ａｒ（Φｒ１，１ ，θｒ１，１ ），…，ａｒ（ΦｒＮｃｌ，Ｎｒａｙ，θｒＮｃｌ，Ｎｒａｙ ）］是維度為Ｎｒ ×Ｎｃｌ Ｎｒａｙ 的接收端天線陣列響應矩陣，Ｗ～ＢＢ維度為Ｎｃｌ Ｎｒａｙ ×Ｎｓ。綜合上述分析，可以得到接收端合并矩陣的設計過程如下。

４ 仿真結果與分析

４． １ 仿真參數說明

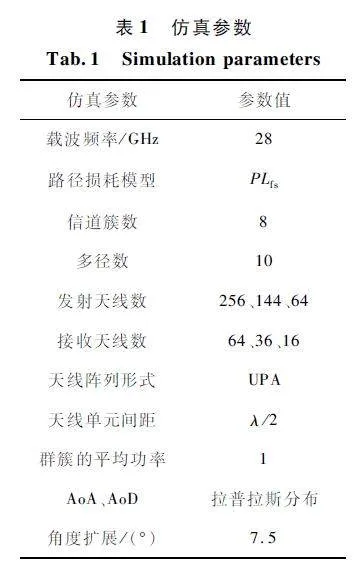
在本小節中，將對全連接結構下單用戶ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ 混合預編碼算法進行仿真分析。仿真參數表１ 所示。

驗證基于ＩｍｐｒｏｖｅｄＯＭＰ 的混合預編碼算法的性能，并將所提出的算法與最優全數字預編碼、基于ＯＭＰ 的混合預編碼算法、基于ＰＥＡｌｔＭｉｎ 的混合預編碼算法進行對比分析。

４． ２ 算法復雜度分析

在本小節中，將提出的ＩｍｐｒｏｖｅｄＯＭＰ 算法的復雜度與其他幾種算法進行評估，即算法中所涉及的計算量。

Ｆｕｌｌ-Ｄｉｇｉｔａｌ 算法的復雜度主要來源于獲取最優預編矩陣，即通過對信道Ｈ 進行ＳＶＤ 可得，因此其復雜度為Ｏ（Ｎ２ｔＮｒ）。ＯＭＰ 算法主要分為三部分：一是通過Ａｔ 和Ｆｒｅｓ 相關性的計算Ｏ（Ｎ２ｔＮＲＦｔ Ｎｓ ）；二是ＦＲＦ 的獲取，即偽逆運算Ｏ（Ｎｔ（ＮＲＦｔ ） ２ ）；三是對ＦＢＢ進行歸一化Ｏ（Ｎｔ ＮＲＦｔ ）。因此，經過循環ＮＲＦｔ 次后，ＯＭＰ 算法的整體復雜度可以近似為Ｏ （Ｎ２ｔＮｒ ＋ＮＲＦｔ （Ｎ２ｔＮＲＦｔ Ｎｓ ＋Ｎｔ（ＮＲＦｔ ） ２ ）＋Ｎｔ ＮＲＦｔ ）。本文提出的Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法的復雜度來自于Ａｔ 和Ｆｒｅｓ 相關性的計算，即為Ｏ （Ｎ２ｔＮＲＦｔ Ｎｓ ），同時涉及ＦＲＦ 的獲取Ｏ（Ｎｔ ＮＲＦｔ ），最后是對ＦＢＢ 歸一化Ｏ（Ｎｔ ＮＲＦｔ ），因此，經過循環ＮＲＦｔ 次后，ＯＭＰ 算法的復雜度近似為Ｏ（Ｎ２ｔＮｒ ＋Ｎ２ｔ（ＮＲＦｔ ） ２ Ｎｓ ＋２Ｎｔ ＮＲＦｔ ）。ＰＥ-ＡｌｔＭｉｎ 算法的復雜度主要來自于ＦＲＦ 的計算，通過提取ＦＢＢ 的相位來更新ＦＲＦ，因此復雜度較高，近似為Ｏ（Ｎ２ｔＮｒ ＋Ｎ２ｔＮＲＦ ＋Ｎｔ ＮＲＦｔ Ｎｓ ＋（ＮＲＦｔ ） ２ Ｎｓ ＋Ｎ３ｔ）。

在Ｍａｓｓｉｖｅ ＭＩＭＯ 系統中，由于Ｎｔ ＞Ｎｒ -ＮＲＦ，算法的復雜度與Ｎｔ 天線數量相關度最強。為了更清晰地展示以上分析結果，并且突出Ｎｔ 和ＮＲＦｔ 對復雜度的貢獻，除去共有的Ｎ２ｔＮｒ 部分，本文將算法復雜度總結如表２ 所示。

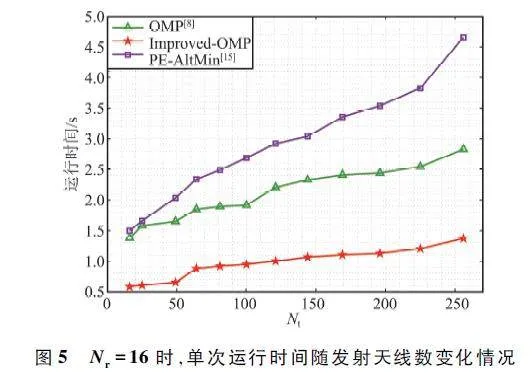
此外，本文也給出了幾種算法的單次運行時間與發射天線數量之間的關系，如圖５ 所示。由圖５可以看出，各種算法的單次運行時間隨著天線數量的增加而增加，本文ＩｍｐｒｏｖｅｄＯＭＰ 算法運行時間最短，表明該算法的復雜度最低。

４． ３ 算法性能分析

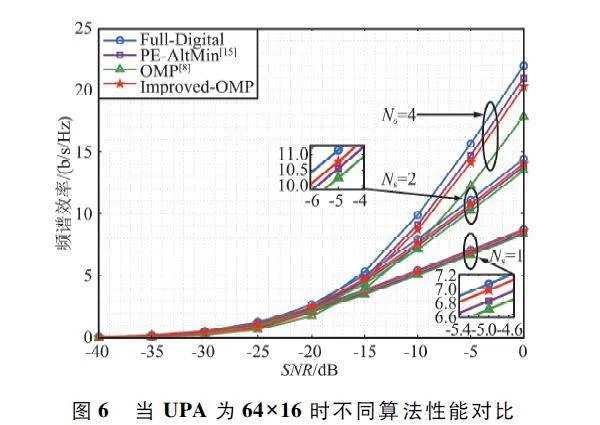
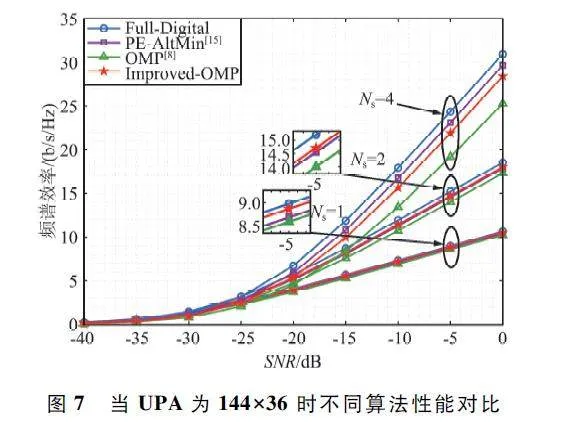
仿真１：當ＮＲＦｔ ＝ ＮＲＦｒ ＝ ４，Ｎｓ ＝ ｛１，２，４｝時，圖６ 和圖７ 分別給出了ＵＰＡ 配置為６４ ×１６ 和１４４ ×３６，全數字預編碼、ＯＭＰ 和基于Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法在傳輸不同數據流時系統頻譜效率與信噪比的關系。

由圖６ 可以看出，隨著信噪比的增加，４ 種算法的系統頻譜效率都響應隨之增加。當傳輸數據流較小時，４ 種算法并沒有明顯的性能差異，但是隨著Ｎｓ的增加，４ 種算法的性能差異隨之增加。

相比較于ＯＭＰ 算法，Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法性能更優。這是因為本文所提算法，對ＯＭＰ 算法中存在的迭代次數過多和矩陣求逆復雜２ 個缺點進行了改進，優化了算法性能。同時，由圖６ 和圖７ 對比可以發現，當天線陣列配置從６４×１６ 增加為１４４×３６ 時，頻譜效率有明顯提升，這也驗證了ＵＰＡ 天線陣列的性質。

此外，由圖６ 和圖７ 可以發現，當ＲＦ Ｃｈａｉｎｓ 數量與傳輸數據流數量相等時，所提出的Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法性能低于ＰＥ-ＡｌｔＭｉｎ 算法，為了尋找具體原因和進行驗證，在仿真２ 中對該情形進行了仿真和分析。

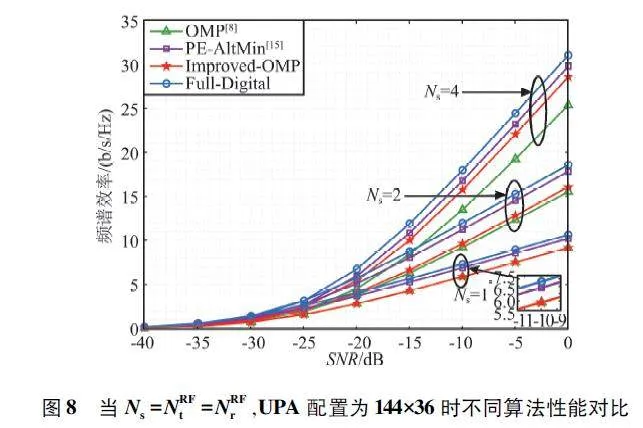
仿真２：當Ｎｓ ＝ ＮＲＦｔ ＝ ＮＲＦｒ ＝ ｛１，２，４｝，圖８ 展示了配置為１４４×３６ 的ＵＰＡ 天線陣列中，４ 種預編碼算法系統頻譜效率與信噪比之間的關系。

由圖８ 可以看出：① 隨著信噪比的增加，４ 種算法的頻譜效率都隨之增加；② 在ＲＦ Ｃｈａｉｎｓ 與數據流數相等情況下，當傳輸單數據流時ＯＭＰ 算法和Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法的性能相同，但隨著數據流的增加，即當數據流大于１ 時，４ 種算法之間的性能差異變得較大，且傳輸的數據流越大，系統頻譜效率提升的效果越明顯；③ 當Ｎｓ ＝ ＮＲＦｔ ＝ ＮＲＦｒ 時，Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法性能始終低于ＰＥ-ＡｌｔＭｉｎ，說明ＰＥ-ＡｌｔＭｉｎ算法更適合傳輸ＲＦ Ｃｈａｉｎｓ 數量與數據流相等的這種情形，這啟發了本文對傳輸的數據流數、ＲＦＣｈａｉｎｓ 對系統性能影響的探討。

此外，幾種算法的系統頻譜效率都隨著數據流的增加而有所提升，說明本文所提出的基于Ｉｍｐｒｏｖｅｄ-ＯＭＰ 的混合預編碼算法更適合于傳輸多數據流的情況。

仿真３：從上面的仿真結果可以發現，ＲＦ Ｃｈａｉｎｓ數量與數據流數之間的關系對系統性能有一定影響。因此，基于仿真２，本文研究了在相同信噪比情況（ＳＮＲ ＝ ０ ｄＢ）時，４ 種預編碼算法的頻譜效率隨ＲＦ Ｃｈａｉｎｓ 數量和傳輸數據流數量變化的情況，如圖９ 所示。

由圖９ 可以看出：① 當ＲＦ Ｃｈａｉｎｓ 數量大于傳輸數據流數量時，基于Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法的性能始終優于ＯＭＰ 算法和ＰＥ-Ａｌｔ 算法；② 隨著ＲＦ Ｃｈａｉｎｓ數量的增加，４ 種算法的頻譜效率隨之增加，這是由于ＲＦ Ｃｈａｉｎｓ 數量越多，可以提供更多的分集增益，獲得更高的頻譜效率，且Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法的系統性能隨著ＲＦ Ｃｈａｉｎｓ 的增加更接近于全數字預編碼的性能；③ 當ＲＦ Ｃｈａｉｎｓ 數量等于數據流時，在傳輸的數據流較小時，Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法性能始終低于ＰＥ-ＡｌｔＭｉｎ 算法，而當傳輸的數據流較大時，Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法性能始終高于ＰＥ-ＡｌｔＭｉｎ 算法。

此外，當ＲＦ Ｃｈａｉｎｓ 數量比傳輸的數據流數量多１ 時，Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法的性能就優于ＰＥ-ＡｌｔＭｉｎ 算法，這是因為在傳輸數據流較大時，多出的一根射偏鏈路提供了額外的分集增益，且給系統保留冗余空間，即ＲＦ Ｃｈａｉｎｓ 路數量滿足Ｎｓ ＜ＮＲＦｔ ＜２Ｎｓ時，可以實現性能和功耗的折中。同時，Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法的性能隨著ＲＦ Ｃｈａｉｎｓ 的增加越來越趨近于全數字預編碼算法。

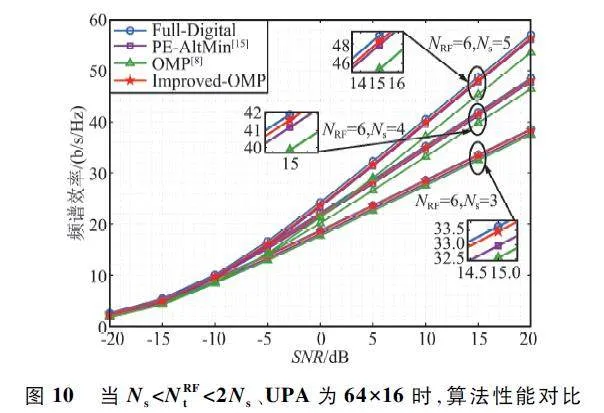
仿真４：為了驗證所提算法的有效性，在Ｎｓ ＜ＮＲＦｔ ＜ ２Ｎｓ 情況下，對Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法與ＰＥ-ＡｌｔＭｉｎ、ＯＭＰ 及全數字預編碼算法進行對比分析，如圖１０ 所示。

由圖１０ 可以看出，在低ＳＮＲ 情況下，幾種算法的性能接近，沒有較大差異；隨著ＳＮＲ 的增加，幾種算法的性能逐漸表現出差異，所提出的算法性能始終優于ＯＭＰ 算法和ＰＥ-ＡｌｔＭｉｎ 算法。此外，隨著數據流與ＲＦ Ｃｈａｉｎｓ 數量的增多，基于Ｉｍｐｒｏｖｅｄ-ＯＭＰ的混合預編碼算法比ＯＭＰ 和ＰＥ-ＡｌｔＭｉｎ 算法在性能上提升的更多，但與最優全數字預編碼算法之間還有一定差距。

５ 結束語

本文針對衛星網絡中全連接結構的ｍｍＷａｖｅＭａｓｓｉｖｅ ＭＩＭＯ 系統，研究了針對單用戶場景的混合預編碼算法。首先，介紹了星地鏈路ｍｍＷａｖｅＭａｓｓｉｖｅ ＭＩＭＯ 系統模型和信道模型；然后，針對ＯＭＰ 算法的不足，提出了一種基于ＯＭＰ 的改進算法ＩｍｐｒｏｖｅｄＯＭＰ，通過選取天線陣列響應矩陣中最優的前ＮＲＦｔ 列向量求解模擬預編碼矩陣ＦＲＦ，同時以逼近目標函數為準則求解數字預編碼矩陣ＦＢＢ ；最后，通過計算機仿真對本文所提出的Ｉｍｐｒｏｖｅｄ-ＯＭＰ 算法進行性能評估，結果表明在Ｎｓ ＜ＮＲＦｔ ＜２Ｎｓ情況下，基于Ｉｍｐｒｏｖｅｄ-ＯＭＰ 的混合預編碼算法在系統性能上更優，且具有更低的計算復雜度。

參考文獻

［１］ ＺＨＡＯ Ｂ Ｋ，ＦＥＩ Ｃ Ｊ，ＭＡＯ Ｘ Ｌ，ｅｔ ａｌ． Ｎｅｔｗｏｒｋｉｎｇ ｉｎＳｐａｃｅ Ｔｅｒｒｅｓｔｒｉａｌ Ｉｎｔｅｇｒａｔｅｄ Ｎｅｔｗｏｒｋｓ［Ｃ］∥２０１９ １８ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｏｐｔｉｃａｌ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ ａｎｄＮｅｔｗｏｒｋｓ （ＩＣＯＣＮ）． Ｈｕａｎｇｓｈａｎ：ＩＥＥＥ，２０１９：１－３．

［２］ ＬＩＵ Ｊ Ｊ，ＳＨＩ Ｙ Ｐ，ＦＡＤＬＵＬＬＡＨ Ｚ Ｍ，ｅｔ ａｌ． ＳｐａｃｅＡｉｒＧｒｏｕｎｄ Ｉｎｔｅｇｒａｔｅｄ Ｎｅｔｗｏｒｋ：Ａ Ｓｕｒｖｅｙ［Ｊ］． ＩＥＥＥ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｓｕｒｖｅｙｓ ＆ Ｔｕｔｏｒｉａｌｓ，２０１８，２０（４）：２７１４－２７４１．

［３］ 李忻，黃繡江，聶在平． ＭＩＭＯ 無線傳輸技術綜述［Ｊ］．無線電工程，２００６，３６（８）：４２－４７．

［４］ ＨＯＹＤＩＳ Ｊ，ＢＲＩＮＫ Ｓ Ｔ，ＤＥＢＢＡＨ Ｍ． Ｍａｓｓｉｖｅ ＭＩＭＯ ｉｎｔｈｅ ＵＬ ／ ＤＬ ｏｆ Ｃｅｌｌｕｌａｒ Ｎｅｔｗｏｒｋｓ：Ｈｏｗ Ｍａｎｙ Ａｎｔｅｎｎａｓ ＤｏＷｅ Ｎｅｅｄ？［Ｊ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｎ Ｓｅｌｅｃｔｅｄ Ａｒｅａｓ ｉｎ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１３，３１（２）：１６０－１７１．

［５］ ＡＨＭＥＤ Ｉ，ＫＨＡＭＭＡＲＩ Ｈ，ＳＨＡＨＩＤ Ａ，ｅｔ ａｌ． Ａ Ｓｕｒｖｅｙ ｏｎＨｙｂｒｉｄ Ｂｅａｍｆｏｒｍｉｎｇ Ｔｅｃｈｎｉｑｕｅｓ ｉｎ ５Ｇ：Ａｒｃｈｉｔｅｃｔｕｒｅ ａｎｄＳｙｓｔｅｍ Ｍｏｄｅｌ Ｐｅｒｓｐｅｃｔｉｖｅｓ［Ｊ］． ＩＥＥＥ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｓｕｒｖｅｙｓ ＆ Ｔｕｔｏｒｉａｌｓ，２０１８，２０（４）：３０６０－３０９７．

［６］ ＭＯＲＳＡＬＩ Ａ，ＮＯＲＯＵＺＩ Ｓ，ＣＨＡＭＰＡＧＮＥＢ． Ｓｉｎｇｌｅ ＲＦＣｈａｉｎ Ｈｙｂｒｉｄ Ａｎａｌｏｇ ／ Ｄｉｇｉｔａｌ Ｂｅａｍｆｏｒｍｉｎｇ ｆｏｒ ｍｍＷａｖｅＭａｓｓｉｖｅＭＩＭＯ［Ｃ］∥ ２０１９ ＩＥＥＥ Ｇｌｏｂａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎＳｉｇｎａｌ ａｎｄ Ｉｎｆｏｒｍａｔｉｏｎ Ｐｒｏｃｅｓｓｉｎｇ （ＧｌｏｂａｌＳＩＰ）． Ｏｔｔａｗａ：ＩＥＥＥ，２０１９：１－５．

［７］ ＷＡＮＧ Ｓ Ｇ，ＬＩ Ｌ Ｆ，ＲＵＢＹ Ｒ，ｅｔ ａｌ． Ａ Ｇｅｎｅｒａｌ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ Ｓｃｈｅｍｅ ｆｏｒ Ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯＳｙｓｔｅｍｓ［Ｊ］． Ｗｉｒｅｌｅｓｓ Ｎｅｔｗｏｒｋｓ，２０２０，２６（２）：１３３１－１３４５．

［８］ ＡＹＡＣＨ Ｅ Ｏ，ＲＡＪＡＧＯＰＡＬ Ｓ，ＡＢＵＳＵＲＲＡ Ｓ，ｅｔ ａｌ． Ｓｐａｔｉａｌｌｙ Ｓｐａｒｓｅ Ｐｒｅｃｏｄｉｎｇ ｉｎ Ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ［Ｊ ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｗｉｒｅｌｅｓｓ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１４，１３（３）：１４９９－１５１３．

［９］ ＬＩＵ Ｘ Ｒ，ＬＩ Ｘ Ｍ，ＣＡＯ Ｓ，ｅｔ ａｌ． Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｆｏｒＭａｓｓｉｖｅ ｍｍＷａｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ ［Ｊ ］． ＩＥＥＥ Ａｃｃｅｓｓ，２０１９，７：３３５７７－３３５８６．

［１０］ ＸＩＥ Ｔ，ＤＡＩ Ｌ，ＧＡＯ Ｘ Ｙ，ｅｔ ａｌ． Ｇｅｏｍｅｔｒｉｃ Ｍｅａｎ Ｄｅｃｏｍｐｏｓｉｔｉｏｎ Ｂａｓｅｄ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ ｍｉｌｌｉｍｅｔｅｒＷａｖｅＭａｓｓｉｖｅ ＭＩＭＯ ［Ｊ ］． Ｃｈｉｎａ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１８，１５（５）：２２９－２３８．

［１１］ ＳＯＨＲＡＢＩ Ｆ，ＹＵ Ｗ． Ｈｙｂｒｉｄ Ｄｉｇｉｔａｌ ａｎｄ Ａｎａｌｏｇ Ｂｅａｍｆｏｒｍｉｎｇ Ｄｅｓｉｇｎ ｆｏｒ Ｌａｒｇｅｓｃａｌｅ Ａｎｔｅｎｎａ Ａｒｒａｙｓ［Ｊ］． ＩＥＥＥＪｏｕｒｎａｌ ｏｆ Ｓｅｌｅｃｔｅｄ Ｔｏｐｉｃｓ ｉｎ Ｓｉｇｎａｌ Ｐｒｏｃｅｓｓｉｎｇ，２０１６，１０（３）：５０１－５１３．

［１２］ ＹＵ Ｘ Ｈ，ＳＨＥＮ Ｊ Ｃ，ＺＨＡＮＧ Ｊ，ｅｔ ａｌ． Ａｌｔｅｒｎａｔｉｎｇ Ｍｉｎｉｍｉｚａｔｉｏｎ Ａｌｇｏｒｉｔｈｍｓ ｆｏｒ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｉｎ ＭｉｌｌｉｍｅｔｅｒＷａｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ ［Ｊ ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｆ ＳｅｌｅｃｔｅｄＴｏｐｉｃｓ ｉｎ Ｓｉｇｎａｌ Ｐｒｏｃｅｓｓｉｎｇ，２０１６，１０（３）：４８５－５００．

［１３］ 徐常志，靳一，李立，等． 面向６Ｇ 的星地融合無線傳輸技術［Ｊ］． 電子與信息學報，２０２１，４３（１）：２８－３６．

［１４］ ＡＲＯＲＡ Ａ，ＴＳＩＮＯＳ Ｃ Ｇ，ＳＨＡＮＫＡＲ Ｂ，ｅｔ ａｌ． ＨｙｂｒｉｄＡｎａｌｏｇＤｉｇｉｔａｌ Ｐｒｅｃｏｄｉｎｇ Ｄｅｓｉｇｎ ｆｏｒ Ｓａｔｅｌｌｉｔｅ Ｓｙｓｔｅｍｓ［Ｃ］∥Ａｄｖａｎｃｅｓ ｉｎ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｓａｔｅｌｌｉｔｅ Ｓｙｓｔｅｍｓ． Ｐｒｏｃｅｅｄｉｎｇｓｏｆ ｔｈｅ ３７ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｓａｔｅｌｌｉｔｅ ＳｙｓｔｅｍｓＣｏｎｆｅｒｅｎｃｅ （ＩＣＳＳＣ－２０１９）． Ｏｋｉｎａｗａ：ＩＥＥＥ，２０１９：１－１３．

［１５］ 李靖，王金海，劉彥剛，等． 衛星通信中相控陣天線的應用及展望［Ｊ］． 無線電工程，２０１９，４９（１２）：１０７６－１０８４．

［１６］ 胡榮，李秀梅，鄧娟，等． 基于混合波束賦形的低軌通信衛星相控陣天線架構研究［Ｊ］． 天地一體化信息網絡，２０２１，２（２）：９０－９７．

［１７］ ＹＯＵ Ｌ，ＱＩＡＮＧ Ｘ Ｙ，ＬＩ Ｋ Ｘ，ｅｔ ａｌ． Ｈｙｂｒｉｄ Ａｎａｌｏｇ ／ ＤｉｇｉｔａｌＰｒｅｃｏｄｉｎｇ ｆｏｒ Ｄｏｗｎｌｉｎｋ Ｍａｓｓｉｖｅ ＭＩＭＯ ＬＥＯ ＳａｔｅｌｌｉｔｅＣｏｍｍｕｎｉｃａｔｉｏｎｓ ［Ｊ ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ＷｉｒｅｌｅｓｓＣｏｍｍｕｎｉｃａｔｉｏｎｓ，２０２２，２１（８）：５９６２－５９７６．

［１８］ ＰＥＮＧ Ｄ Ｙ，ＬＩ Ｙ，ＣＨＡＴＺＩＮＯＴＡＳ Ｓ，ｅｔ ａｌ． ＨｙｂｒｉｄＡｎａｌｏｇＤｉｇｉｔａｌ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ ｍｍＷａｖｅ Ｃｏｅｘｉｓｔｉｎｇ ｉｎ ５Ｇｓａｔｅｌｌｉｔｅ Ｉｎｔｅｇｒａｔｅｄ Ｎｅｔｗｏｒｋ［Ｃ］∥２０２０ ＩＥＥＥ ３１ｓｔ ＡｎｎｕａｌＩｎｔｅｒｎａｔｉｏｎａｌ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ｐｅｒｓｏｎａｌ，Ｉｎｄｏｏｒ ａｎｄ ＭｏｂｉｌｅＲａｄｉｏ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ． Ｌｏｎｄｏｎ：ＩＥＥＥ，２０２０：１－６．

［１９］ ＭＹＳＯＲＥ Ｂ Ｓ，ＬＡＧＵＮＡＳ Ｅ，ＣＨＡＴＺＩＮＯＴＡＳＳ，ｅｔ ａｌ． Ｐｒｅｃｏｄｉｎｇ ｆｏｒ Ｓａｔｅｌｌｉｔｅ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ：Ｗｈｙ，Ｈｏｗ ａｎｄ ＷｈａｔＮｅｘｔ？［Ｊ］． ＩＥＥＥ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｌｅｔｔｅｒｓ，２０２１，２５（８）：２４５３－２４５７．

［２０］ 陳強，王田，薛仁魁，等． 基于數字波束形成技術的北斗抗干擾終端研究［Ｊ］． 無線電工程，２０２３，５３ （５）：１０９３－１１０１．

［２１］ ＲＡＰＰＡＰＯＲＴ Ｔ Ｓ，ＨＥＡＴＨ ＪＲ Ｒ Ｗ，ＤＡＮＩＥＬＳＲ Ｃ，ｅｔ ａｌ．Ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ Ｗｉｒｅｌｅｓｓ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ［Ｍ］． ［Ｓ． ｌ． ］：Ｐｅａｒｓｏｎ Ｅｄｕｃａｔｉｏｎ，２０１５．

［２２］ ＸＵ Ｈ，ＫＵＫＳＨＹＡ Ｖ，ＲＡＰＰＡＰＯＲＴ Ｔ Ｓ． Ｓｐａｔｉａｌ ａｎｄＴｅｍｐｏｒａｌ Ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ ｏｆ ６０ＧＨｚ Ｉｎｄｏｏｒ Ｃｈａｎｎｅｌｓ［Ｊ］．ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｎ Ｓｅｌｅｃｔｅｄ Ａｒｅａｓ ｉｎ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２００２，２０（３）：６２０－６３０．

［２３］ ＦＯＲＥＮＺＡ Ａ，ＬＯＶＥ Ｄ Ｊ，ＨＥＡＴＨ Ｒ Ｗ． ＳｉｍｐｌｉｆｉｅｄＳｐａｔｉａｌ Ｃｏｒｒｅｌａｔｉｏｎ Ｍｏｄｅｌｓ ｆｏｒ Ｃｌｕｓｔｅｒｅｄ ＭＩＭＯ Ｃｈａｎｎｅｌｓｗｉｔｈ Ｄｉｆｆｅｒｅｎｔ Ａｒｒａｙ Ｃｏｎｆｉｇｕｒａｔｉｏｎｓ ［Ｊ ］． ＩＥＥＥＴｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｖｅｈｉｃｕｌａｒ Ｔｅｃｈｎｏｌｏｇｙ，２００７，５６ （４ ）：１９２４－１９３４．

作者簡介

胡家榮 男，（１９９４—），碩士研究生。主要研究方向：智能通信、預編碼。

（*通信作者）李伊陶 男，（１９９１—），博士，副教授。主要研究方向：天空地一體化網絡、智能通信等。

熊興中 男，（１９７１—），博士，教授。主要研究方向：人工智能、物聯網技術、無線通信技術等。

基金項目：四川省科技廳項目（２０２３ＮＳＦＳＣ１９８７）；人工智能四川省重點實驗室開放基金（２０２１ＲＺＪ０１）；四川輕化工大學研究生創新基金（Ｙ２０２１０５５）