格上身份基簡短關聯環簽名及其電子投票應用

摘 要：環簽名具備匿名性，身份基環簽名無需證書，關聯環簽名可避免用戶重復簽名，但這些簽名占用空間多且效率低。針對這些問題，先輸出公共參數和系統主密鑰，再提取用戶密鑰，然后使用格上的累加器對環中公鑰進行累加，并將知識證明簽名推廣至格上，構造出格上身份基簡短關聯環簽名。對該簽名的不可偽造性、關聯性和匿名性進行了證明。對簽名方案進行了性能分析與實驗評估，結果表明，該簽名節省了時間開銷和存儲空間。利用該簽名及門限秘密共享技術，提出后量子的電子投票協議。

關鍵詞：格；身份基；知識證明簽名；累加器；簡短關聯環簽名；門限秘密共享；電子投票

中圖分類號：ＴＰ３０９． ２ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１０６（２０２４）０５－１３０８－１２

０ 引言

環簽名是一種簡化的群簽名，可有效提高用戶的匿名性［１］。身份基環簽名是基于身份的密碼體制與環簽名相結合使用戶不再需要證書的簽名，與之類似，無證書環簽名也是不需要證書的簽名；門限環簽名是將門限機制應用至環簽名；關聯環簽名具有簽名人關聯性，通過關聯標簽，可確定某２ 個簽名是否由某用戶代表同一群體簽署產生，即可避免用戶重復簽名，一次性環簽名也具有類似的性質。但是，這些簽名的長度均隨著環成員的增多而增大。簡短關聯環簽名［２－３］先使用累加器對環中公鑰進行累加，再進行知識證明簽名，在保留關聯環簽名一些特性的情況下，簽名長度不會隨環成員數量的變化而變化［４］。然而上述這些簽名均基于傳統數學難題，隨著量子計算技術的發展，它們的安全性在降低。基于格的密碼體制具有以下優點：格上任意實例的安全度都相同；格中運算以線性運算和模運算為主，運算簡單；至今沒有可行的量子算法能夠破解格上的困難問題，因而其備受學者們關注［５－７］。

電子投票在人類社會活動中發揮著非常重要的作用，其安全性、公平性、公正性等問題一直是公眾關注的焦點，且影響其廣泛地推廣使用。將簡短關聯環簽名應用至電子投票，首先可提高投票者的匿名性，其次能避免重復投票的發生，再次簽名長度固定不變可節省存儲空間；如果再結合格理論，可使得投票具備抗量子性，更加安全。

文獻［８］提出一種關聯環簽名方案，實現了簽名的批量驗證。文獻［９］利用關聯環簽名，設計了基于智能合約的電子投票方案。文獻［１０］利用一次性環簽名及匿名地址技術，提出一個以太坊電子投票方案。文獻［１１］提出了關聯環簽密，并將其應用至智能合約電子投票。這些方案均可確保投票者的匿名性，同時避免出現重復投票的情況。但是，這些方案的簽名（簽密）長度均隨著環成員的增多而增大。文獻［２－３］構造了簡短關聯環簽名，隨著環成員的增多，簽名長度不變。文獻［１２］提出了一個簡短關聯環簽名方案，適用于電子現金協議。文獻［１３］提出了新的高效的簡短關聯接環簽名，并將其應用于智能合約電子投票。但是，上述所有簽名方案均是基于傳統數論困難問題，不具備抗量子性。

基于格上的困難問題，文獻［１４］提出了切合實際的格基一次性關聯環簽名方案，實用性強。針對傳統身份基關聯環簽名不能抵抗量子攻擊的問題，文獻［７］構造了一個格上身份基的關聯環簽名方案。文獻［１５］提出了格上無證書環簽名（Ｌａｔｔｉｃｅ-Ｂａｓｅｄ Ｃｅｒｔｉｆｉｃａｔｅｌｅｓｓ Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅ，ＬＣＲＳ），其中含有類似關聯標簽的密鑰鏡像，減少了簽名階段的采樣次數，提高了簽名效率。文獻［１６］結合了基于模糊身份的簽名和環簽名，提出了一種格上基于模糊身份的環簽名方案（Ｆｕｚｚｙ Ｉｄｅｎｔｉｔｙ-Ｂａｓｅｄ Ｒｉｎｇ Ｓｉｇｎａ-ｔｕｒｅ ｆｒｏｍ Ｌａｔｔｉｃｅｓ，ＬＦＩＢＲＳ）。針對自動泊車系統中的隱私安全問題，文獻［１７］提出了一個基于格的環簽名方案。通過判斷２ 個集合中相同元素的個數是否達到一定數量作為關聯性的判斷條件。文獻［１８］構建了一種新的格上身份基的關聯環簽名方案（Ｉｄｅｎｔｉｔｙ-Ｂａｓｅｄ Ｌｉｎｋａｂｌｅ Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅ Ｓｃｈｅｍｅｏｎ Ｌａｔｔｉｃｅｓ，Ｌ＿ＩＢＬＲＳ）。文獻［１９］提出一種格上的關聯環簽名方案，并基于此構建了區塊鏈上的流行病控制系統。文獻［２０］利用格理論增加抗量子性，并應用消息塊共享技術和填充排列技術，構造格上的門限關聯環簽名以適應一種新的電子投票場景。

然而上述這些方案的簽名長度隨著環成員的增多而增大，且運算效率低。文獻［２１］提出了一種格上的簡短關聯環簽名，雖然簽名長度固定，但其生成過程中使用較多的哈希運算，導致其不可偽造性證明及匿名性證明不夠嚴謹，且沒有實際應用方案。文獻［２２］提出了一種基于格的無證書環簽名方案（Ｃｅｒｔｉｆｉｃａｔｅ Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅ Ｓｃｈｅｍｅ Ｂａｓｅｄ ｏｎ Ｌａｔｔｉｃｅ，Ｌ-ＣＲＳＳ），在后量子時代具有較高的安全性。文獻［２３］也提出了一種格上的環簽名方案，并將其應用至匿名電子投票。這２ 種簽名方案的簽名長度不會隨環成員數量的變化而變化，但是比較長，占用空間多，且方案的運算效率低。

上述方案存在著簽名占用存儲空間多、運算效率低等問題。針對這些問題，本文提出新的方案，主要貢獻如下：

① 首先輸出公共參數并秘密保存系統主密鑰，其次根據用戶身份提取出用戶密鑰，再次使用格上的累加器對環中公鑰進行累加計算，然后將傳統的知識證明簽名推廣至格上，最后構造出格上的身份基簡短關聯環簽名。對簽名方案的不可偽造性、關聯性和匿名性進行了嚴謹的證明。

② 將所構造的簽名方案應用至電子投票，結合（ｔ，ｎ）門限秘密共享技術，提出后量子的電子投票協議，分別設計了協議的注冊、管理、投票、收集和計票等算法。

因為Ｌ-ＣＲＳＳ 中含有多次的矩陣間乘法運算及ＳａｍｐｌｅＭａｔ 算法，其矩陣間乘法耗時遠高于其他方案中的矩陣向量乘法耗時，顯然ＴＬＣＲＳＳ 最大。文獻［７］方案中的矩陣向量乘法為Zｎ×（ｍ＋１） ｑ 中的矩陣乘以 Zｑｍ＋１ 中的向量，文獻［１７］方案的矩陣向量乘法為Zｎ×ｍ ｑ 中的矩陣乘以 Zｍｑ中的向量，本方案的矩陣向量乘法主要為Z ｎ×ｎ ｑ「 ｌｂ ｑ」 中的矩陣乘以｛０，１｝ ｎ ｌｂ ｑ 中的向量，ｑ ＝Ｏ ～ （ｎ）≥３，ｍ≥５ｎｌｂ ｑ，顯然本方案的矩陣向量乘法運算量是最小的，ＴＭＶ 也是最小的。另外，雖然本方案含有多次的ｂｉｎ 算法，但是該算法耗費時間很少，而文獻［７ ］方案中還含有多次的ＳａｍｐｌｅＤｏｍ 算法，文獻［１７］方案中也含有多次的ＴｒａｐＧｅｎ 及ＳａｍｐｌｅＤｏｍ 算法，因此本方案的總時間開銷是相對較小的。

這幾種方案的存儲開銷對比如表１ 最后一列所示，主要從方案的簽名長度進行對比。本方案生成的簽名長度為ｎ「 ｌｂ ｑ」 ＋（２ｎ＋ｎ ｌｂ ｑ」 ＋ｍ＋３）ｌｂ ｑ，ＬＣＲＳＳ 的簽名長度為（２ｍ＋ｎｍ）ｌｂ ｑ，文獻［７］的簽名長度為［（ｍ＋１）Ｎ＋ｎ＋２］ｌｂ ｑ，文獻［１７］的簽名長度為（ｍＮ＋κ）ｌｂ ｑ。對比后發現，隨著環成員數量Ｎ 的增大，文獻［７，１７］的簽名長度會隨之增大，而本方案及ＬＣＲＳＳ 的簽名長度固定不變，較節省空間。

４． ２ 實驗評估

本文的實驗在配置為Ｉｎｔｅｌ Ｃｏｒｅ ｉ７１０７５０Ｈ 處理器、８ ＧＢ 內存、５１２ ＧＢ 固態硬盤、６４ 位Ｗｉｎｄｏｗｓ １０操作系統的計算機上運行，根據文中對參數的取值要求及安全考慮，同時參考其它相關文獻，將參數設置為ｎ ＝ ８，ｍ ＝ １ ２８０，ｑ ＝ ２３２ ＝ ４ ２９４ ９６７ ２９６。

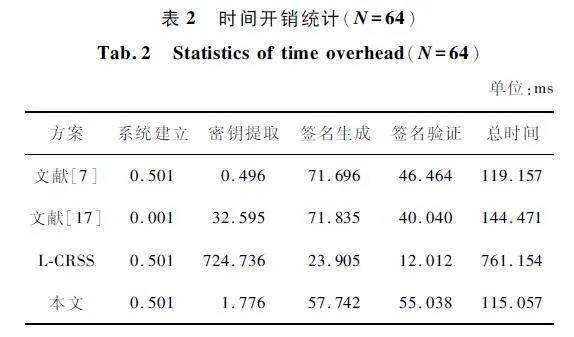
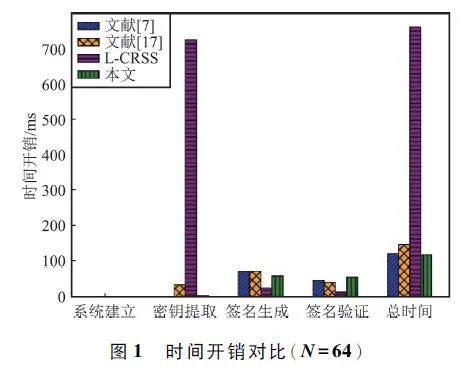
表２ 為各簽名方案在各階段及總的時間開銷，環成員個數為６４，進而根據表２ 中的數據，各簽名方案的時間開銷對比如圖１ 所示。

從圖１ 和表２ 可以看出，Ｌ-ＣＲＳＳ 的密鑰提取時間和總時間開銷最大，文獻［７，１７］及本文方案的總時間開銷均比較小；根據４． １ 節的分析可知，Ｌ-ＣＲＳＳ 中含有多次的矩陣間乘法運算（主要為Z８×１ ２８０ ４ ２９４ ９６７ ２９６ 與｛－４０，－３９，…，０，…，３９，４０｝ １ ２８０×２００ 中的矩陣相乘）和ＳａｍｐｌｅＭａｔ 算法，文獻［７，１７］及本文方案僅含有矩陣向量乘法運算，ＴＭＭ 遠高于ＴＭＶ ，故而如此。

從表２ 和圖１ 中還可以看出，文獻［１７］的總時間開銷大于文獻［７］，文獻［７］的總時間開銷大于本方案。因為ｎ ＝ ８，ｍ ＝ １ ２８０，ｑ ＝ ２３２ ＝ ４ ２９４ ９６７ ２９６，再結合４． １ 節的總時間開銷分析，即可解釋這里的實驗結果。

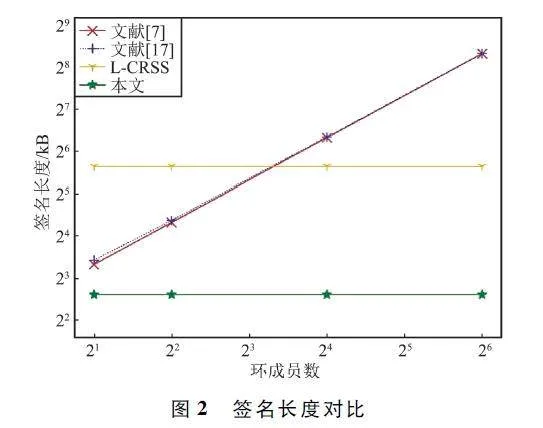
表３ 為各方案的存儲開銷統計，進而根據表３中的數據，畫出各簽名方案的簽名長度對比如圖２所示。從圖２ 和表３ 可以看出，隨著環成員個數的增大，文獻［７，１７］的簽名長度均在增大且非常接近，Ｌ-ＣＲＳＳ 和本方案的簽名長度保持不變，但本方案的簽名長度最小。這是因為ｎ ＝ ８，ｍ ＝ １ ２８０，ｑ ＝２３２ ＝ ４ ２９４ ９６７ ２９６，κ ＝ ２００，再結合４． １ 節中的簽名長度分析，也可解釋這里的實驗結果。

５ 電子投票應用

５． １ 電子投票協議

本文構造的格上身份基簡短關聯環簽名方案適用于電子投票應用，因為：① 簽名方案的不可偽造性可有效防止用戶偽造選票；② 簽名方案的隱私性可確保投票者的隱私；③ 簽名方案的關聯性可有效防止用戶重復投票；④ 本簽名方案可為電子投票應用節省存儲空間和時間開銷。

所以將本文簽名方案應用于電子投票，同時為防止任何實體獲得投票中間結果，確保選票的隱私性，引入（ｔ，ｎ）門限秘密共享技術，提出電子投票協議。該協議包含實體：投票者Ｖｉ（擁有身份ＩＤｉ ）、注冊機構ＫＧＣ（即密鑰生成中心，為投票者們生成密鑰）、管理機構ＭＡ（擁有私鑰ＳＫＭＡ 和公鑰ＰＫＭＡ ）、計票機構ＣＴｉ（共ｎ－１ 個，即ｉ∈［２，ｎ］），投票協議包含以下幾個算法：

① 注冊

注冊機構ＫＧＣ 運行Ｓｅｔｕｐ（１ｎ）算法輸出公共參數ｐｐ ＝ （Ａ，Ｃ，Ｈ０ ，Ｈ１ ），秘密保存系統主密鑰ＭＳＫ ＝Ｔ。投票者Ｖｉ 把其身份ＩＤｉ 提交給ＫＧＣ 審核，在審核通過之后Ｖｉ 注冊成功。ＫＧＣ 運行算法ＫｅｙＥｘｔ（ＩＤｉ，ＭＳＫ，ｐｐ）為投票者Ｖｉ 生成ｄｉ ＝ｂｉｎ（Ｈ０（ＩＤｉ）ｍｏｄｑ）及私鑰ｋｉ，滿足Ａ·ｋｉ ＝ Ｇ·ｄｉ。

② 管理

ｆ（１），ｆ（２ ），… ，ｆ（ｎ），其中ｆ 為隨機多項式。投票者Ｖｉ 選擇其他投票者的身份信息（包含其自身）組成環Ｒ ＝ ｛ＩＤ０ ，ＩＤ１ ，… ，ＩＤＮ－１ ｝，Ｖｉ 運行Ｓｉｇｎ（ｐｐ，ｋｉ，ｆ（１），Ｒ）為選票的秘密份額ｆ（１ ）生成簽名σｉＲ（ｆ（１））＝ （ｕ，ｉｉ，ｂｉ１，ｒｉ１，ｃｉ１，ｚｉ１），之后Ｖｉ 將信息（σｉＲ（ｆ（１）），Ｒ，ｆ（１））通過匿名信道發送給管理機構ＭＡ。ＭＡ 先驗證σｉＲ（ｆ（１））的有效性，無效則拒絕接收這條信息；若簽名有效，則檢查關聯標簽ｉｉ是否已存儲在數據庫中，若已經存儲則意味著Ｖｉ 重復投票，ＭＡ 拒絕接收這條信息；否則ＭＡ 將（ｉｉ，ｆ（１））存入數據庫。之后ＭＡ 計算φｉ ←ＳａｍｐｌｅＰｒｅ（ＰＫＭＡ，ＳＫＭＡ，ｉｉ，ｓ），并將φｉ 返回給Ｖｉ。

③ 投票

投票者Ｖｉ 檢驗ＰＫＭＡ·φｉ ＝？ｉｉ，若等式不成立，則重新要求ＭＡ 發送φｉ；若等式成立，則Ｖｉ 運行Ｓｉｇｎ（ｐｐ，ｋｉ，ｆ（ｊ），Ｒ）為選票μ 的其他秘密份額ｆ（ｊ）（其中ｊ ＝ ２，３，…，ｎ）生成簽名σｉＲ（ｆ（ｊ））＝ （ｕ，ｉｉ，ｂｉｊ，ｒｉｊ，ｃｉｊ，ｚｉｊ）。之后，Ｖｉ 通過匿名信道將信息（σｉＲ （ｆ（ｊ），ｆ（１），φｉ）（ｊ ＝ ２，３，…，ｎ）分別發送給各計票機構ＣＴｊ（ｊ ＝ ２，３，…，ｎ）。ＣＴｊ 驗證簽名σｉＲ（ｆ（ｊ））的有效性，若有效則公布（ｊ，ｉｉ，ｆ（１））。

④ 收集

若投票者Ｖｉ 發現其（ｊ，ｉｉ，ｆ（１））未被公布，則其出示（ｆ（１），φｉ）以抗議，管理機構ＭＡ 會要求ＣＴｊ 加入與（ｊ，ｉｉ，ｆ （１ ））對應的選票份額簽名信息（即（σ ｉＲ（ｆ（ｊ）），ｆ（ｊ），ｆ（１），φｉ））。

⑤ 計票

在投票及收集結束之后，因為每個ＣＴｊ 除了掌握各自的ｆ（ｊ）（ｊ∈［２，ｎ］）之外，均還掌握ｆ（１），所以根據（ｔ，ｎ）門限方案，（ｔ－１）個計票機構ＣＴｊ 即可將投票者Ｖｉ 的選票μ 恢復出來，然后統計票數。

５． ２ 協議分析

合法性：協議的注冊算法可有效防止未注冊用戶進行投票，確保了投票的合法性；

公正性：本協議利用門限秘密共享可有效防止任何實體在投票結束前獲得投票的中間結果，簽名方案的不可偽造性可防止惡意用戶偽造選票，從而確保了投票的公正性；

隱私性：門限秘密共享可以保證選票的隱私性，簽名方案的匿名性可確保投票者的隱私性，從而確保了電子投票協議的隱私性；

唯一性：本協議利用簽名方案的關聯性可防止投票者重復投票，確保投票的唯一性；

完備性：協議的收集算法防止計票機構漏計選票，確保了計票的完備性；

抗量子性：協議中的簽名方案是基于格理論的，可有效抵抗量子攻擊；

實用性：本協議節省了選票簽名的存儲空間，提高了運算效率，在后量子時代具有實用性。

６ 結束語

根據格上身份基的關聯環簽名，以及簡短關聯環簽名，將知識證明簽名推廣至格上，提出格上身份基簡短關聯環簽名方案，包含系統建立、密鑰提取、簽名生成、簽名驗證和簽名關聯等５ 個算法。基于格上的困難問題證明了簽名方案的不可偽造性，同時還證明了簽名方案的關聯性和匿名性。通過性能分析和實驗評估發現，該簽名方案節省了時間和存儲開銷。將簽名方案應用至電子投票，結合（ｔ，ｎ）門限秘密共享技術，提出電子投票協議，包含注冊、管理、投票、收集和計票等算法。由于所基于的簽名方案以及協議中的算法設計，協議具備合法性、公正性、隱私性、投票唯一性、完備性、抗量子性和實用性。

在未來的工作中，計劃進一步提升簽名效率，并結合區塊鏈技術，提出后量子時代基于區塊鏈的安全電子投票協議，確保投票的公開透明安全高效，以便更好地為社會服務。

參考文獻

［１］ 蔡曉晴，鄧堯，張亮，等． 區塊鏈原理及其核心技術［Ｊ］．計算機學報，２０２１，４４（１）：８４－１３１．

［２］ ＴＳＡＮＧ Ｐ Ｐ，ＷＥＩ Ｖ Ｋ． Ｓｈｏｒｔ Ｌｉｎｋａｂｌｅ Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅｓ ｆｏｒＥｖｏｔｉｎｇ，Ｅｃａｓｈ ａｎｄ Ａｔｔｅｓｔａｔｉｏｎ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ１ｓｔ Ｉｎｆｏｒｍａｔｉｏｎ Ｓｅｃｕｒｉｔｙ Ｐｒａｃｔｉｃｅ ａｎｄ Ｅｘｐｅｒｉｅｎｃｅ Ｃｏｎｆｅｒｅｎｃｅ． Ｓｉｎｇａｐｏｒｅ：Ｓｐｒｉｎｇｅｒ，２００５：４８－６０．

［３］ ＡＵ Ｍ Ｈ，ＣＨＯＷ Ｓ Ｓ Ｍ，ＳＵＳＩＬＯ Ｗ，ｅｔ ａｌ． Ｓｈｏｒｔ ＬｉｎｋａｂｌｅＲｉｎｇ Ｓｉｇｎａｔｕｒｅｓ Ｒｅｖｉｓｉｔｅｄ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ３ｒｄＥｕｒｏｐｅａｎ Ｐｕｂｌｉｃ Ｋｅｙ Ｉｎｆｒａｓｔｒｕｃｔｕｒｅ Ｗｏｒｋｓｈｏｐ． Ｔｕｒｉｎ：Ｓｐｒｉｎｇｅｒ，２００６：１０１－１１５．

［４］ ＹＵ Ｂ，ＬＩＵ Ｊ Ｋ，ＳＡＫＺＡＤ Ａ，ｅｔ ａｌ． ＰｌａｔｆｏｒｍｉｎｄｅｐｅｎｄｅｎｔＳｅｃｕｒｅ Ｂｌｏｃｋｃｈａｉｎｂａｓｅｄ Ｖｏｔｉｎｇ Ｓｙｓｔｅｍ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓｏｆ ｔｈｅ ２１ｓｔ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｉｎｆｏｒｍａｔｉｏｎ Ｓｅｃｕｒｉｔｙ Ｃｏｎｆｅｒｅｎｃｅ．Ｇｕｉｌｄｆｏｒｄ：Ｓｐｒｉｎｇｅｒ，２０１８：３６９－３８６．

［５］ 田苗苗，黃劉生，楊威． 高效的基于格的環簽名方案［Ｊ］． 計算機學報，２０１２，３５（４）：７１２－７１８．

［６］ 賈小英，何德彪，許芷巖，等． 格上高效的基于身份的環簽名體制［Ｊ］． 密碼學報，２０１７，４（４）：３９２－４０４．

［７］ 湯永利，夏菲菲，葉青，等． 格上基于身份的可鏈接環簽名［Ｊ］． 密碼學報，２０２１，８（２）：２３２－２４７．

［８］ 王啟宇，陳杰，莊立爽． 智能電網中可鏈接環簽名的批量驗證［Ｊ］． 密碼學報，２０２０，７（５）：６１６－６２７．

［９］ ＬＹＵ Ｊ Ｚ，ＪＩＡＮＧ Ｚ Ｌ，ＷＡＮＧ Ｘ，ｅｔ ａｌ． Ａ Ｓｅｃｕｒｅ Ｄｅｃｅｎｔｒａｌｉｚｅｄ Ｔｒｕｓｔｌｅｓｓ Ｅｖｏｔｉｎｇ Ｓｙｓｔｅｍ Ｂａｓｅｄ ｏｎ Ｓｍａｒｔ Ｃｏｎｔｒａｃｔ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ １８ｔｈ ＩＥＥＥ ＩｎｔｅｒｎａｔｉｏｎａｌＣｏｎｆｅｒｅｎｃｅ ｏｎ Ｔｒｕｓｔ，Ｓｅｃｕｒｉｔｙ ａｎｄ Ｐｒｉｖａｃｙ ｉｎ Ｃｏｍｐｕｔｉｎｇａｎｄ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ． Ｒｏｔｏｒｕａ：ＩＥＥＥ，２０１９：５７０－５７７．

［１０］ 鄭劍，賴恒財． 基于一次性環簽名的區塊鏈電子投票方案［Ｊ］． 計算機應用研究，２０２０，３７（１１）：３３７８－３３８１．

［１１］ 王杰昌，張平，高遠，等． 融合可鏈接環簽密的智能合約電子投票協議［Ｊ］． 計算機工程，２０２２，４８ （４ ）：１２６－１３２．

［１２］ 王玲玲，張國印，馬春光． 適用于電子現金協議的簡短關聯環簽名方案［Ｊ］． 北京郵電大學學報，２００８，３１（１）：１０２－１０６．

［１３］ 王杰昌，張平，段瑩，等． 結合簡短可鏈接環簽名的智能合約選舉方案［Ｊ］． 計算機工程與應用，２０２３，５９（６）：２５８－２６７．

［１４］ ＢＡＵＭ Ｃ，ＬＩＮ Ｈ，ＯＥＣＨＳＮＥＲ Ｓ． Ｔｏｗａｒｄｓ ＰｒａｃｔｉｃａｌＬａｔｔｉｃｅｂａｓｅｄ Ｏｎｅｔｉｍｅ Ｌｉｎｋａｂｌｅ Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅｓ ［Ｃ］∥Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｉｎｆｏｒｍａｔｉｏｎａｎｄ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｓｅｃｕｒｉｔｙ． Ｌｉｌｌｅ：Ｓｐｒｉｎｇｅｒ，２０１８：３０３－３２２．

［１５］ ＺＨＡＮＧ Ｍ Ｗ，ＣＨＥＮ Ｘ Ｂ． Ａ Ｐｏｓｔｑｕａｎｔｕｍ ＣｅｒｔｉｆｉｃａｔｅｌｅｓｓＲｉｎｇ Ｓｉｇｎａｔｕｒｅ Ｓｃｈｅｍｅ ｆｏｒ Ｐｒｉｖａｃｙｐｒｅｓｅｒｖｉｎｇ ｏｆＢｌｏｃｋｃｈａｉｎ Ｓｈａｒｉｎｇ Ｅｃｏｎｏｍｙ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ａｒｔｉｆｉｃｉａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ ａｎｄＳｅｃｕｒｉｔｙ． Ｄｕｂｌｉｎ：Ｓｐｒｉｎｇｅｒ，２０２１：２６５－２７８．［１６］ ＣＡＯ Ｃ Ｔ，ＹＯＵ Ｌ，ＨＵ Ｇ Ｒ． Ｆｕｚｚｙ Ｉｄｅｎｔｉｔｙｂａｓｅｄ ＲｉｎｇＳｉｇｎａｔｕｒｅ ｆｒｏｍ Ｌａｔｔｉｃｅｓ［Ｊ］． Ｓｅｃｕｒｉｔｙ ａｎｄ ＣｏｍｍｕｎｉｃａｔｉｏｎＮｅｔｗｏｒｋｓ，２０２１，２０２１：１－９．

［１７］ ＸＵ Ｓ Ｙ，ＣＨＥＮ Ｘ，ＷＡＮＧ Ｃ，ｅｔ ａｌ． Ａ Ｌａｔｔｉｃｅｂａｓｅｄ ＲｉｎｇＳｉｇｎａｔｕｒｅ Ｓｃｈｅｍｅ ｔｏ Ｓｅｃｕｒｅ Ａｕｔｏｍａｔｅｄ Ｖａｌｅｔ Ｐａｒｋｉｎｇ［Ｃ］∥Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ １６ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎＷｉｒｅｌｅｓｓ Ａｌｇｏｒｉｔｈｍｓ，Ｓｙｓｔｅｍｓ，ａｎｄ Ａｐｐｌｉｃａｔｉｏｎｓ（ＷＡＳＡ）．Ｎａｎｊｉｎｇ：Ｓｐｒｉｎｇｅｒ，２０２１：７０－８３．

［１８］ 曹成堂，游林，胡耿然． 一種新的格上基于身份的可鏈接環簽名方案［Ｊ］． 密碼學報，２０２２，９（６）：９６９－９８１．

［１９］ ＣＨＥＮ Ｘ，ＸＵ Ｓ Ｙ，ＣＡＯ Ｙ Ｂ，ｅｔ ａｌ． ＡＱＲＳ：Ａｎｔｉｑｕａｎｔｕｍ"Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅ Ｓｃｈｅｍｅ ｆｏｒ Ｓｅｃｕｒｅ Ｅｐｉｄｅｍｉｃ Ｃｏｎｔｒｏｌ ｗｉｔｈ"Ｂｌｏｃｋｃｈａｉｎ［Ｊ］． Ｃｏｍｐｕｔｅｒ Ｎｅｔｗｏｒｋｓ，２０２３，２２４：１０９５９５．

［２０］ 莊立爽，陳杰，王啟宇． 電子投票協議下的基于格的可鏈接門限環簽名［Ｊ］． 密碼學報，２０２１，８（３）：４０２－４１６．

［２１］ 王杰昌，張平，李杰，等． 格上的簡短可鏈接環簽名［Ｊ］． 計算機應用研究，２０２２，３９（９）：２８４３－２８４９．

［２２］ ＤＯＮＧ Ｓ Ｓ，ＺＨＯＵ Ｙ Ｈ，ＹＡＮＧ Ｙ Ｇ，ｅｔ ａｌ． ＡＣｅｒｔｉｆｉｃａｔｅｌｅｓｓ Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅ Ｓｃｈｅｍｅ Ｂａｓｅｄ ｏｎ Ｌａｔｔｉｃｅ［Ｊ］． Ｃｏｎｃｕｒｒｅｎｃｙ ａｎｄ Ｃｏｍｐｕｔａｔｉｏｎ：Ｐｒａｃｔｉｃｅ ａｎｄ Ｅｘｐｅｒｉｅｎｃｅ，２０２２，３４（２８）：ｅ７３８５．

［２３］ ＺＨＯＵ Ｙ Ｈ，ＤＯＮＧ Ｓ Ｓ，ＹＡＮＧ Ｙ Ｇ． Ｒｉｎｇ ＳｉｇｎａｔｕｒｅＳｃｈｅｍｅ Ｂａｓｅｄ ｏｎ Ｌａｔｔｉｃｅ ａｎｄ Ｉｔｓ Ａｐｐｌｉｃａｔｉｏｎ ｏｎＡｎｏｎｙｍｏｕｓ Ｅｌｅｃｔｒｏｎｉｃ Ｖｏｔｉｎｇ ［Ｊ］． ＫＳＩＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎＩｎｔｅｒｎｅｔ ａｎｄ Ｉｎｆｏｒｍａｔｉｏｎ Ｓｙｓｔｅｍｓ，２０２２，１６（１）：２８７－３０４．

［２４］ ＧＥＮＴＲＹ Ｃ，ＰＥＩＫＥＲＴ Ｃ，ＶＡＩＫＵＮＴＡＮＡＴＨＡＮ Ｖ．Ｔｒａｐｄｏｏｒｓ ｆｏｒ Ｈａｒｄ Ｌａｔｔｉｃｅｓ ａｎｄ Ｎｅｗ Ｃｒｙｐｔｏｇｒａｐｈｉｃ Ｃｏｎｓｔｒｕｃｔｉｏｎｓ［Ｃ］∥Ｐｒｏｃｅｅｄｉｎｇ ｏｆ ｔｈｅ １４ｔｈ Ａｎｎｕａｌ ＡＣＭ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ｔｈｅｏｒｙ ｏｆ Ｃｏｍｐｕｔｉｎｇ． Ｖｉｃｔｏｒｉａ：ＡＣＭ，２００８：１９７－２０６．

［２５］ ＬＩＢＥＲＴ Ｂ，ＬＩＮＧ Ｓ，ＮＧＵＹＥＮ Ｋ，ｅｔ ａｌ． ＺｅｒｏｋｎｏｗｌｅｄｇｅＡｒｇｕｍｅｎｔｓ ｆｏｒ Ｌａｔｔｉｃｅｂａｓｅｄ Ａｃｃｕｍｕｌａｔｏｒｓ：Ｌｏｇａｒｉｔｈｍｉｃｓｉｚｅ Ｒｉｎｇ Ｓｉｇｎａｔｕｒｅｓ ａｎｄ Ｇｒｏｕｐ Ｓｉｇｎａｔｕｒｅｓ ｗｉｔｈｏｕｔ Ｔｒａｐｄｏｏｒｓ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ３５ｔｈ Ａｎｎｕａｌ ＩｎｔｅｒｎａｔｉｏｎａｌＣｏｎｆｅｒｅｎｃｅ ｏｎ ｔｈｅ Ｔｈｅｏｒｙ ａｎｄ Ａｐｐｌｉｃａｔｉｏｎｓ ｏｆ ＣｒｙｐｔｏｇｒａｐｈｉｃＴｅｃｈｎｉｑｕｅｓ （ＥＵＲＯＣＲＹＰＴ）． Ｖｉｅｎｎａ：Ｓｐｒｉｎｇｅｒ，２０１６：１－３１．

［２６］ ＣＡＭＥＮＩＳＣＨ Ｊ，ＳＴＡＤＬＥＲ Ｍ． Ｅｆｆｉｃｉｅｎｔ Ｇｒｏｕｐ ＳｉｇｎａｔｕｒｅＳｃｈｅｍｅｓ ｆｏｒ Ｌａｒｇｅ Ｇｒｏｕｐｓ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ １７ｔｈＡｎｎｕａｌ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｒｙｐｔｏｌｏｇｙ Ｃｏｎｆｅｒｅｎｃｅ． Ｓａｎｔａ Ｂｏｒｂａｒａ：Ｓｐｒｉｎｇｅｒ，１９９７：４１０－４２４．

［２７］ ＬＹＵＢＡＳＨＥＶＳＫＹ Ｖ． Ｌａｔｔｉｃｅ Ｓｉｇｎａｔｕｒｅｓ ｗｉｔｈｏｕｔ Ｔｒａｐｄｏｏｒｓ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ３１ｓｔ Ａｎｎｕａｌ ＩＡＣＲ ＥｕｒｏｃｒｙｐｔＩｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ ｔｈｅ Ｔｈｅｏｒｙ ａｎｄ Ａｐｐｌｉｃａｔｉｏｎｓｏｆ Ｃｒｙｐｔｏｇｒａｐｈｉｃ Ｔｅｃｈｎｉｑｕｅｓ． Ｃａｍｂｒｉｄｇｅ：Ｓｐｒｉｎｇｅｒ，２０１２：７３８－７５５．

作者簡介

王杰昌 男，（１９８５—），碩士，講師。主要研究方向：信息安全、區塊鏈隱私保護。

劉牧華 男，（１９８７—），博士，副教授。主要研究方向：密碼學、信息安全。

張 平 男，（１９７６—），博士，教授。主要研究方向：密碼學、信息安全。

（*通信作者）劉玉嶺 男，（１９８２—），博士，正高級工程師。主要研究方向：網絡安全態勢感知、網安大數據分析。

于景茹 女，（１９８２—），碩士，副教授。主要研究方向：信息安全。

張 斌 男，（１９８０—），博士，高級工程師。主要研究方向：信息安全。

基金項目：基礎加強計劃技術領域基金（２０２１-ＪＣＪＱ-ＪＪ-０９０８ ）；國家自然科學基金（６２１０２１３４ ）；河南省科技攻關項目（２３２１０２２１０１３８，２３２１０２２１０１３０）；龍門實驗室重大科技項目（２３１１００２２０３００）；河南省高等學校重點科研項目（２３Ａ５２００４６，２３Ａ４１３００５）