促進思維發展的數學習題設計

劉大勇

以思維能力發展為導向設計數學習題，有助于提高學生分析問題、解決問題的能力，培養學生的數學核心素養。本文結合具體案例闡釋促進中學生思維發展的數學習題設計策略。

設計變式練習，提升遷移能力。教師可以通過變更數學對象或數學問題的呈現形式促進知識遷移，幫助學生鞏固基礎，提升思維能力。

以《坐標系內圖形對稱》復習課為例，筆者設計了“說出點P（x，y）關于x軸、y軸和原點對稱點的坐標”題目及如下變式問題。

變式問題1：說出直線y=2x-1關于x軸、y軸和原點對稱的解析式。

變式問題2：說出雙曲線[y=1x]關于x軸、y軸和原點對稱的解析式。

變式問題3：說出拋物線[y=3x2+2x-1]關于x軸、y軸和原點對稱的解析式。

變式問題4：以下函數（y=3x，[y=x2]，[y=2x3]，[y=-1x]，[y=2x]）圖象關于x軸對稱的有? ? ?，關于y軸對稱的有? ? ?，關于原點對稱的有? ? ?。

這道題從最基本的點的對稱出發，引導學生歸納出幾類對稱點的坐標特點；接著，把點對稱的問題變式為直線對稱的問題（變式問題1），引導學生理解直線對稱本質上是直線上的點對稱，只要找到直線上任意兩個點的對稱點坐標，就可以根據待定系數法求出解析式；然后，繼續變式為雙曲線、拋物線的問題（變式問題2、變式問題3），這些問題均可類比作答變式問題1的方法求出解析式；最后的變式問題4不僅出現其他類型的函數，還改變了問題的呈現形式，引導學生根據解析式畫出圖象，再根據圖象確定對稱性。變式問題讓學生在知識遷移與運用中感受到從一般到特殊的研究過程，體會到函數的對稱最終都可轉化為點的對稱。

設計開放問題，提供思維發展空間。開放性問題能提供更廣闊的思維空間，有利于滿足不同層次水平學生的學習需求。教學《相似三角形》時，教師設計了以下兩個問題。

問題1：一個鋼筋三角形框架三邊長分別為20cm，50cm，60cm，現要再做一個與其相似的鋼筋三角形框架，而只有長為30cm和50cm的兩根鋼筋，要求以其中的一根為一邊，從另一根截下兩段（允許有余料）作為另兩邊，有幾種不同的截法？

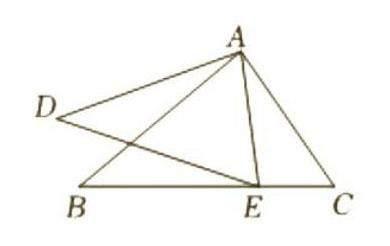
問題2：如圖，如果∠BAD=∠CAE，那么添加條件? ? ? ? ?，能確定△ABC和△ADE相似。

教師設置如下問題引導學生思考問題1：把一根鋼筋截成兩段，有幾種情況？兩個三角形的對應邊確定了嗎，有幾種對應情況？學生根據“三角形任意兩邊之和大于第三邊”，確定只能用50cm的鋼筋來截，設截得的兩段分別為xcm和ycm，則有以下三種對應情況：①[2030=50x=60y]，得x=75，y=90（不合題意，舍去）；②[20x=5030=60y]，得x=12，y=36；③[20x=50y=6030]，得x=10，y=25。筆者引導學生逐一分析上述三種情況，完整地解題。

對問題2，由∠BAD=∠CAE可得∠DAE=∠BAC，從“兩角分別對應相等的兩個三角形相似”考慮，可添加∠D=∠B或∠AED=∠C條件，從“兩邊成比例且夾角相等的兩個三角形相似”考慮，可添加[ADAB=AEAC]條件。筆者設置此類解法靈活、具有一定探索性的題目，能讓學生從不同角度思考問題，為思維發展提供空間。

（作者單位：浙江省杭州市桐廬縣三合初級中學）

責任編輯? 張敏